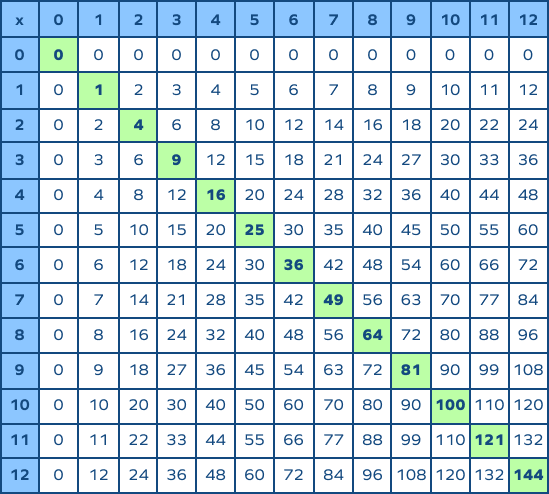
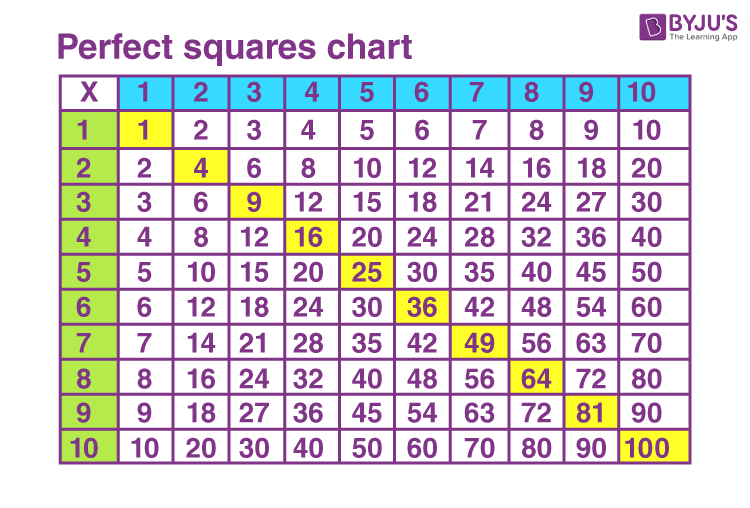
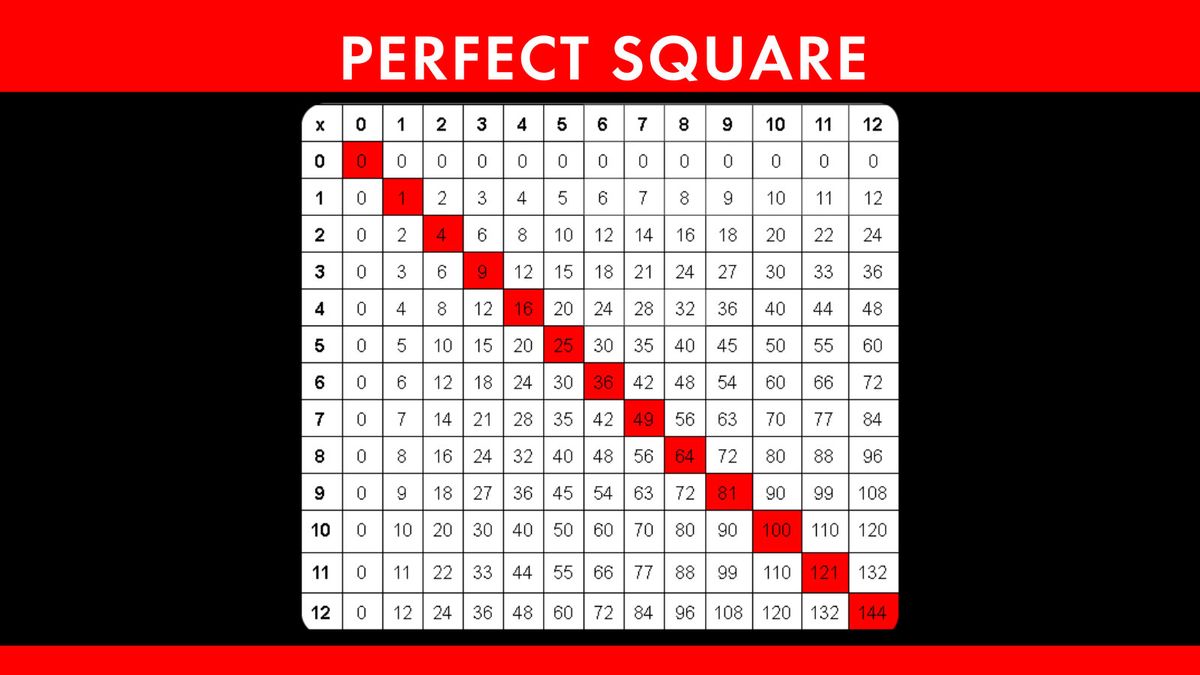
Topic square root problems worksheet: Square root problems worksheets are essential tools for students to master the concept of square roots. These worksheets offer a variety of problems that help in understanding and practicing square roots, enhancing mathematical skills and confidence. Explore our collection to find the perfect worksheet for your learning needs.
Table of Content
- Square Root Problems Worksheet
- Introduction to Square Roots
- Understanding and Finding Square Roots
- Square Root Calculation Methods
- Square Roots of Negative Numbers
- Practice Worksheets and Exercises
- Solving Square Root Equations
- Word Problems Involving Square Roots
- Square Roots in Algebra
- Square Roots in Geometry
- Interactive Square Root Activities
- Additional Resources and References
- YOUTUBE: Video này giải thích về khái niệm căn bậc hai, cung cấp hướng dẫn dễ hiểu về cách tính toán và ứng dụng của chúng.
Square Root Problems Worksheet
Explore various worksheets to help students master square roots. These resources are suitable for different grade levels and cover a range of concepts related to square roots.
Finding Square Roots
- Worksheets for finding the square roots of numbers using factorization and long division methods, catering to 6th, 7th, and 8th grades.
- Printable worksheets for practice, including examples such as finding the square root of 144, √784, and √2401.
Simplifying Square Roots
- Learn to simplify square roots with both positive and negative numbers.
- Examples include simplifying expressions like √-144 and √-196.
Square Root Operations
- Worksheets on adding, subtracting, multiplying, and dividing square roots.
- Includes square roots of fractions and decimals.
Grade-Specific Worksheets
- Grade 6: Finding radicals in square roots, adding and subtracting square roots.
- Grade 8: Estimation, using calculators for complex square roots, and higher-order questions aligned with Common Core Standard 8.EE.2.
Interactive and Printable Resources
- Printable PDFs and interactive worksheets to cater to different learning preferences.
- Resources include detailed explanations and step-by-step solutions.
Advanced Topics
- Challenging problems involving square roots of complex numbers.
- Worksheets designed for advanced students to push their understanding further.
These worksheets are designed to make learning square roots engaging and effective. Whether you are a teacher looking for classroom resources or a parent seeking additional practice for your child, these worksheets provide comprehensive coverage of square root topics.
| Topic | Description |
|---|---|
| Finding Square Roots | Basic worksheets for finding square roots using different methods. |
| Simplifying Square Roots | Worksheets to practice simplifying square roots, including negative numbers. |
| Square Root Operations | Practice worksheets on operations involving square roots. |
| Grade-Specific | Worksheets tailored to specific grade levels with appropriate difficulty. |
| Interactive and Printable | Mix of printable PDFs and interactive online worksheets. |
| Advanced Topics | Challenging worksheets for advanced learners. |

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical concepts used to determine a value which, when multiplied by itself, gives the original number. For example, the square root of 16 is 4, because \( 4 \times 4 = 16 \). Understanding square roots is crucial for progressing in algebra, geometry, and other advanced math topics.
The square root symbol is \( \sqrt{} \). To express the square root of a number \( n \), we write \( \sqrt{n} \). For example, \( \sqrt{25} = 5 \).
There are several key properties and rules associated with square roots:
- For any positive number \( a \), \( \sqrt{a^2} = a \).
- The square root of a product is the product of the square roots: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- The square root of a quotient is the quotient of the square roots: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) for \( b \neq 0 \).
Let's look at a few examples to illustrate these properties:
| \(\sqrt{9}\) | = 3 |
| \(\sqrt{16}\) | = 4 |
| \(\sqrt{25}\) | = 5 |
Square roots are not always whole numbers. For example, \( \sqrt{2} \approx 1.414 \) and is an irrational number, meaning it cannot be expressed as a simple fraction.
Understanding square roots also includes learning about perfect squares. A perfect square is an integer that is the square of another integer. For example, 1, 4, 9, 16, 25 are all perfect squares.
Using these concepts, students can solve various types of problems, including simplifying expressions and solving equations involving square roots.
Understanding and Finding Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because \(5 \times 5 = 25\). In mathematical notation, the square root of \(x\) is denoted as \(\sqrt{x}\).
Square roots can be found using several methods, including factorization, long division, and approximation. Here's a step-by-step guide to understanding and finding square roots:
- Prime Factorization: Break down the number into its prime factors. Group the prime factors into pairs, and take one number from each pair to multiply together to get the square root.
- Long Division Method: This method is useful for larger numbers. It involves dividing the number into pairs of digits starting from the decimal point and finding the largest number whose square is less than or equal to the number.
- Using a Calculator: For quick results, especially with non-perfect squares, a calculator can be used. Most scientific calculators have a square root function.
Here are some examples to illustrate these methods:
| Number | Prime Factorization | Square Root |
|---|---|---|
| 36 | \(36 = 2^2 \times 3^2 \) | \( \sqrt{36} = 6 \) |
| 81 | \(81 = 3^4 \) | \( \sqrt{81} = 9 \) |
| 50 | \(50 = 2 \times 5^2 \) | \( \sqrt{50} = 5\sqrt{2} \approx 7.07 \) |
Square roots are not limited to positive numbers. The square root of a negative number introduces the concept of imaginary numbers. The square root of -1 is denoted as \(i\), so the square root of any negative number can be expressed in terms of \(i\).
Understanding square roots is essential for solving quadratic equations, working with areas in geometry, and simplifying expressions in algebra. By mastering the methods of finding square roots, students can tackle a wide range of mathematical problems with confidence.
Square Root Calculation Methods
Calculating square roots can be approached through several methods. Understanding these methods can help solve square root problems more efficiently. Here, we detail three primary methods: prime factorization, estimation, and using a calculator.
Prime Factorization Method
This method involves breaking down the number into its prime factors. Here's a step-by-step guide:
- Find the prime factors of the number.
- Pair the prime factors.
- Take one factor from each pair and multiply them together to get the square root.
Example: To find the square root of 144 using prime factorization:
- Prime factors of 144 are: 2 × 2 × 2 × 2 × 3 × 3
- Pairing the factors: (2 × 2), (2 × 2), (3 × 3)
- Taking one from each pair: 2 × 2 × 3 = 12
- So, √144 = 12
Estimation Method
The estimation method is useful when a calculator is not available and the number is not a perfect square. Here’s how to estimate:
- Find the two closest perfect squares between which the number lies.
- Estimate the square root to a number between the roots of these perfect squares.
- Refine the estimate by squaring your estimate and adjusting accordingly.
Example: To estimate the square root of 50:
- The closest perfect squares are 49 (72) and 64 (82).
- Estimate between 7 and 8. Since 50 is closer to 49, try 7.1 or 7.2.
- Refine: 7.12 = 50.41, so the estimate is close.
Using a Calculator
This is the most straightforward method. Follow these steps:
- Turn on the calculator.
- Press the square root (√) button.
- Enter the number you want the square root of.
- Press the equals (=) button to get the result.
Example: To find the square root of 144 using a calculator:
- Press √, then type 144.
- Press = to get the result, which is 12.
Square Roots of Negative Numbers
In mathematics, the square root of a negative number is not a real number. This is because there is no real number that, when squared, results in a negative number. To deal with the square roots of negative numbers, we use the concept of imaginary numbers.
An imaginary number is defined as a number that can be written as a real number multiplied by the imaginary unit i, where i is defined by the property:
\[
i^2 = -1
\]
Using this definition, we can express the square root of any negative number. For example, the square root of -1 is written as:
\[
\sqrt{-1} = i
\]
For a general negative number, say -a, where a is a positive real number, the square root can be expressed as:
\[
\sqrt{-a} = \sqrt{a} \cdot i
\]
Here are the steps to find the square root of a negative number:
- Identify the negative number for which you want to find the square root.
- Write the number as the product of -1 and a positive number. For example, -9 can be written as -1 × 9.
- Take the square root of the positive number. For instance, the square root of 9 is 3.
- Multiply the result by i. Hence, the square root of -9 is \( 3i \).
Let's look at a few more examples:
- \(\sqrt{-4} = 2i\)
- \(\sqrt{-16} = 4i\)
- \(\sqrt{-25} = 5i\)
Imaginary numbers are fundamental in various branches of mathematics and engineering. They are especially important in fields such as electrical engineering, signal processing, and quantum physics.
In summary, while real numbers are sufficient for most everyday calculations, the introduction of imaginary numbers allows us to solve equations that involve the square roots of negative numbers. This expands our ability to model and solve complex problems in advanced mathematics and science.

Practice Worksheets and Exercises
Below are several practice worksheets and exercises designed to help students master the concept of square roots. These worksheets include a variety of problems, ranging from basic square root calculations to more complex applications in algebra and geometry. Use these exercises to reinforce learning and assess understanding.
- Finding Square Roots:
- Find the square root of the following numbers:
- \(\sqrt{144}\)
- \(\sqrt{256}\)
- \(\sqrt{625}\)
- Estimate the square root of the following numbers (to the nearest tenth):
- \(\sqrt{50}\)
- \(\sqrt{75}\)
- \(\sqrt{120}\)
- Find the square root of the following numbers:
- Square Root Operations:
- Simplify the following expressions:
- \(\sqrt{45} + \sqrt{20}\)
- \(\sqrt{72} - \sqrt{32}\)
- \(\sqrt{98} \times \sqrt{2}\)
- Divide the square roots and simplify:
- \(\frac{\sqrt{81}}{\sqrt{9}}\)
- \(\frac{\sqrt{144}}{\sqrt{16}}\)
- Simplify the following expressions:
- Square Roots of Fractions and Decimals:
- Find the square root of the following fractions:
- \(\sqrt{\frac{1}{4}}\)
- \(\sqrt{\frac{9}{16}}\)
- Calculate the square root of the following decimals:
- \(\sqrt{0.49}\)
- \(\sqrt{1.44}\)
- Find the square root of the following fractions:
- Word Problems:
- A square garden has an area of 225 square meters. What is the length of one side of the garden?
- The area of a square is 64 square inches. Find the perimeter of the square.
- Challenge Problems:
- Simplify and find the value of \(\sqrt{50} + \sqrt{32}\).
- If \(\sqrt{x} = 12\), what is the value of \(x\)?
These worksheets are designed to help students gain confidence in working with square roots, develop problem-solving skills, and apply their knowledge to real-world situations. Encourage students to work through these exercises, and provide additional practice as needed.
Solving Square Root Equations
Square root equations involve finding the value of the variable that makes the equation true. Below are the steps to solve square root equations along with some examples.
Steps to Solve Square Root Equations
- Isolate the Square Root: If the equation has a square root term, isolate it on one side of the equation.
- Square Both Sides: Once the square root is isolated, square both sides of the equation to eliminate the square root.
- Simplify and Solve: Solve the resulting equation for the variable.
- Check Your Solution: Substitute the solution back into the original equation to ensure it satisfies the equation. This step is crucial because squaring both sides can introduce extraneous solutions.
Examples
Let's go through a couple of examples to illustrate these steps.
Example 1
Solve the equation \( \sqrt{x+3} = 5 \)
- Isolate the square root: \( \sqrt{x+3} = 5 \)
- Square both sides: \( (\sqrt{x+3})^2 = 5^2 \)
- Simplify: \( x+3 = 25 \)
- Solve for \( x \): \( x = 25 - 3 \)
\( x = 22 \) - Check the solution: \( \sqrt{22+3} = \sqrt{25} = 5 \), which is true. So, \( x = 22 \) is a valid solution.
Example 2
Solve the equation \( \sqrt{2x - 1} = x - 3 \)
- Isolate the square root: \( \sqrt{2x - 1} = x - 3 \)
- Square both sides: \( (\sqrt{2x - 1})^2 = (x - 3)^2 \)
- Simplify: \( 2x - 1 = x^2 - 6x + 9 \)
- Rearrange the equation: \( x^2 - 8x + 10 = 0 \)
- Solve the quadratic equation using the quadratic formula: \( x = \frac{8 \pm \sqrt{64 - 40}}{2} \)
\( x = \frac{8 \pm \sqrt{24}}{2} \)
\( x = \frac{8 \pm 2\sqrt{6}}{2} \)
\( x = 4 \pm \sqrt{6} \) - Check the solutions: For \( x = 4 + \sqrt{6} \), \( \sqrt{2(4 + \sqrt{6}) - 1} = 4 + \sqrt{6} - 3 \) holds true. For \( x = 4 - \sqrt{6} \), check if it holds in the original equation.
Practice Problems
Try solving the following square root equations:
- \( \sqrt{3x + 7} = x + 2 \)
- \( \sqrt{5x - 4} = x - 1 \)
- \( \sqrt{4x + 1} = x + 3 \)
Remember to check each solution by substituting it back into the original equation to ensure it does not produce any extraneous solutions.
Additional Tips
- Be cautious of extraneous solutions that may arise when squaring both sides of an equation.
- If you encounter a quadratic equation, use the quadratic formula to find potential solutions.
- Always verify your solutions by substituting them back into the original equation.
Word Problems Involving Square Roots
Word problems that involve square roots require translating real-world situations into mathematical expressions and solving for unknowns. These problems often deal with areas, volumes, distances, and other practical applications. Below are some examples and steps to solve word problems involving square roots:
-
Problem: A square garden has an area of 144 square feet. What is the length of each side of the garden?
Solution: To find the side length of the square, we take the square root of the area.
Let \( A \) be the area of the square.
Here, \( A = 144 \, \text{sq ft} \).
The side length \( s \) is given by \( s = \sqrt{A} \).
Thus, \( s = \sqrt{144} = 12 \, \text{ft} \).
-
Problem: The diagonal of a square screen measures 10 inches. What is the length of each side of the screen?
Solution: Use the Pythagorean theorem for a square, where the diagonal \( d \) is given by \( d = s\sqrt{2} \).
Let \( s \) be the side length of the square.
The equation is \( d = s\sqrt{2} \).
Substitute \( d = 10 \) inches into the equation: \( 10 = s\sqrt{2} \).
Solve for \( s \): \( s = \frac{10}{\sqrt{2}} = \frac{10 \sqrt{2}}{2} = 5\sqrt{2} \) inches.
-
Problem: A cylindrical tank has a radius of 5 feet and a height of 20 feet. Calculate the volume of the tank and then determine the side length of a cube that has the same volume.
Solution:
Volume of the cylinder \( V \) is given by \( V = \pi r^2 h \).
Substitute \( r = 5 \, \text{ft} \) and \( h = 20 \, \text{ft} \):
\( V = \pi \times 5^2 \times 20 = 500\pi \, \text{cubic feet} \).
The volume of a cube is \( V = s^3 \), where \( s \) is the side length.
Set the volumes equal: \( s^3 = 500\pi \).
Solve for \( s \): \( s = \sqrt[3]{500\pi} \, \text{ft} \).
-
Problem: A right triangle has a hypotenuse of 13 cm and one leg measuring 5 cm. Find the length of the other leg.
Solution: Use the Pythagorean theorem \( a^2 + b^2 = c^2 \).
Let \( a \) and \( b \) be the legs, and \( c \) be the hypotenuse.
Given \( c = 13 \, \text{cm} \) and \( a = 5 \, \text{cm} \).
Substitute into the equation: \( 5^2 + b^2 = 13^2 \).
Solve for \( b \): \( 25 + b^2 = 169 \).
\( b^2 = 144 \).
\( b = \sqrt{144} = 12 \, \text{cm} \).
When solving word problems involving square roots, always follow these steps:
- Read the problem carefully and identify the quantities involved.
- Translate the problem into mathematical terms.
- Set up an equation using the relevant formula.
- Solve for the unknowns by applying algebraic operations and square roots.
- Check your solution by substituting it back into the context of the problem.
Square Roots in Algebra
Square roots play a fundamental role in algebra, appearing in equations, functions, and various algebraic expressions. Understanding how to manipulate and solve equations involving square roots is crucial for solving a wide range of algebraic problems. Below are detailed explanations and examples of square roots in algebra:
-
Solving Equations with Square Roots: To solve equations involving square roots, isolate the square root expression and then square both sides of the equation to eliminate the square root.
Example: Solve \( \sqrt{2x + 3} = 5 \)
Isolate the square root: \( \sqrt{2x + 3} = 5 \)
Square both sides: \( (\sqrt{2x + 3})^2 = 5^2 \)
Simplify: \( 2x + 3 = 25 \)
Solve for \( x \): \( 2x = 25 - 3 \)
\( 2x = 22 \)
\( x = 11 \)
-
Equations with Square Root Terms: Sometimes, equations include terms with and without square roots. Isolate the square root term and solve by squaring the equation. Be sure to check for extraneous solutions.
Example: Solve \( \sqrt{x + 1} = x - 1 \)
Isolate the square root: \( \sqrt{x + 1} = x - 1 \)
Square both sides: \( (\sqrt{x + 1})^2 = (x - 1)^2 \)
Simplify: \( x + 1 = x^2 - 2x + 1 \)
Rearrange the equation: \( 0 = x^2 - 3x \)
Factorize: \( 0 = x(x - 3) \)
Solutions: \( x = 0 \) or \( x = 3 \)
Check solutions in the original equation:
For \( x = 0 \): \( \sqrt{0 + 1} = 0 - 1 \rightarrow \text{false} \).
For \( x = 3 \): \( \sqrt{3 + 1} = 3 - 1 \rightarrow \text{true} \).
Valid solution: \( x = 3 \).
-
Square Roots in Functions: Functions involving square roots often require domain restrictions to ensure the argument of the square root is non-negative.
Example: Consider the function \( f(x) = \sqrt{4 - x} \)
Determine the domain: \( 4 - x \geq 0 \).
Solve: \( x \leq 4 \).
Domain: \( (-\infty, 4] \).
Range: Since the square root function outputs non-negative values, the range is \( [0, \infty) \).
-
Rationalizing Denominators: To simplify expressions involving square roots in the denominator, multiply the numerator and denominator by the conjugate or a suitable term to eliminate the square root from the denominator.
Example: Simplify \( \frac{3}{\sqrt{2}} \)
Multiply by \( \frac{\sqrt{2}}{\sqrt{2}} \):
\( \frac{3}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{3\sqrt{2}}{2} \).
-
Complex Numbers: Square roots of negative numbers introduce complex numbers. For example, \( \sqrt{-4} = 2i \), where \( i \) is the imaginary unit.
Example: Simplify \( \sqrt{-9} \)
Express as a product of \( \sqrt{9} \) and \( \sqrt{-1} \):
\( \sqrt{-9} = \sqrt{9} \cdot \sqrt{-1} = 3i \).
Understanding these concepts will enable you to handle algebraic problems involving square roots effectively. Practice solving various problems and check your solutions to ensure accuracy.

Square Roots in Geometry
Square roots are integral in various geometric calculations, especially when dealing with lengths, areas, and distances. They often appear in problems involving right triangles, circles, and the Pythagorean theorem. Below are detailed explanations and examples of how square roots are used in geometry:
-
Using the Pythagorean Theorem: The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (\(c\)) is equal to the sum of the squares of the other two sides (\(a\) and \(b\)). This theorem is used to find the length of a side in a right triangle.
Formula: \( c = \sqrt{a^2 + b^2} \)
Example: Find the hypotenuse of a right triangle with legs of 6 cm and 8 cm.
Apply the formula: \( c = \sqrt{6^2 + 8^2} \)
Calculate: \( c = \sqrt{36 + 64} = \sqrt{100} = 10 \, \text{cm} \).
-
Distance Formula: The distance between two points in a plane is derived from the Pythagorean theorem and involves square roots.
Formula: \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
Example: Find the distance between points \( (1, 2) \) and \( (4, 6) \).
Apply the formula: \( d = \sqrt{(4 - 1)^2 + (6 - 2)^2} \)
Calculate: \( d = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \).
-
Diagonal of a Rectangle: The diagonal of a rectangle can be found using the Pythagorean theorem since the diagonal forms a right triangle with the sides of the rectangle.
Formula: \( d = \sqrt{l^2 + w^2} \)
Example: Find the diagonal of a rectangle with length 9 m and width 12 m.
Apply the formula: \( d = \sqrt{9^2 + 12^2} \)
Calculate: \( d = \sqrt{81 + 144} = \sqrt{225} = 15 \, \text{m} \).
-
Area of an Equilateral Triangle: The area can be found using the formula involving the square root of 3.
Formula: \( A = \frac{\sqrt{3}}{4} s^2 \)
Example: Find the area of an equilateral triangle with side length 6 cm.
Apply the formula: \( A = \frac{\sqrt{3}}{4} \times 6^2 \)
Calculate: \( A = \frac{\sqrt{3}}{4} \times 36 = 9\sqrt{3} \, \text{cm}^2 \).
-
Radius of a Circle Inscribed in a Right Triangle: The radius of an inscribed circle can be found using the area and the semiperimeter of the triangle.
Formula: \( r = \frac{A}{s} \), where \( A \) is the area, and \( s \) is the semiperimeter.
Example: Find the radius of a circle inscribed in a right triangle with legs 3 cm and 4 cm.
Find the hypotenuse: \( c = \sqrt{3^2 + 4^2} = 5 \, \text{cm} \).
Calculate the area: \( A = \frac{1}{2} \times 3 \times 4 = 6 \, \text{cm}^2 \).
Find the semiperimeter: \( s = \frac{3 + 4 + 5}{2} = 6 \, \text{cm} \).
Apply the formula: \( r = \frac{6}{6} = 1 \, \text{cm} \).
-
Diagonal of a Cube: The space diagonal of a cube can be found using the formula derived from the Pythagorean theorem in three dimensions.
Formula: \( d = s\sqrt{3} \)
Example: Find the space diagonal of a cube with side length 4 cm.
Apply the formula: \( d = 4\sqrt{3} \, \text{cm} \).
These applications illustrate how square roots are essential in solving geometric problems. Mastering these concepts will enable you to tackle a variety of geometric calculations with confidence.
Interactive Square Root Activities
Interactive activities are an engaging way to explore square roots, offering hands-on learning and practical applications. These activities include games, puzzles, digital tools, and collaborative exercises. Here are some interactive activities designed to enhance understanding of square roots:
-
Square Root Matching Game: Create a set of cards with numbers and their corresponding square roots. Students match pairs of cards.
Setup: Prepare cards with numbers like 1, 4, 9, 16, 25 and separate cards with square roots 1, 2, 3, 4, 5.
Activity: Lay out the cards face down. Players take turns flipping over two cards to find matching pairs.
Objective: Match the number card with its correct square root card.
-
Square Root Number Line: Use a number line to visualize the placement of square roots between integers.
Setup: Draw a large number line on a board or use a digital tool.
Activity: Mark positions for square roots such as \( \sqrt{2} \), \( \sqrt{3} \), \( \sqrt{5} \) and ask students to approximate their locations between integers.
Objective: Understand the relative positions of square roots on the number line.
-
Digital Square Root Calculator: Use online square root calculators to explore square roots of various numbers interactively.
Setup: Provide links to online square root calculators or apps.
Activity: Input different numbers and observe the results. Challenge students to find square roots of non-perfect squares.
Objective: Familiarize with square root calculations and explore decimal approximations.
-
Square Root Puzzle: Create puzzles where students solve for missing numbers using square root operations.
Setup: Design a grid or puzzle with missing values that can be found using square roots.
Activity: Provide clues that involve calculating or estimating square roots to complete the puzzle.
Objective: Apply square root knowledge in a problem-solving context.
-
Interactive Graphing Tool: Use graphing calculators or software to plot functions involving square roots.
Setup: Provide access to graphing tools like Desmos or GeoGebra.
Activity: Graph functions such as \( y = \sqrt{x} \) or \( y = \sqrt{x + 2} \) and explore transformations and properties.
Objective: Visualize how square root functions behave and change.
-
Square Root Race: Organize a timed challenge where students solve square root problems to move across a game board.
Setup: Design a game board with checkpoints requiring square root calculations.
Activity: Students solve problems at each checkpoint to advance. The first to reach the end wins.
Objective: Reinforce square root skills in a competitive and fun setting.
-
Square Root Scavenger Hunt: Set up a scavenger hunt with clues that require finding or calculating square roots to progress.
Setup: Prepare clues related to square roots hidden around the classroom or use a digital platform.
Activity: Students solve each clue to find the next location or task.
Objective: Engage in hands-on learning by solving square root problems in a scavenger hunt format.
-
Virtual Escape Room: Create a virtual escape room where solving square root problems helps unlock the next level.
Setup: Use a digital platform to design an escape room with square root challenges.
Activity: Students solve square root problems to find codes or clues to advance through the virtual room.
Objective: Enhance square root skills in an interactive and immersive environment.
These interactive activities offer diverse and engaging ways to practice and understand square roots, making learning both effective and enjoyable.
Additional Resources and References
To further your understanding and practice of square roots, here are some valuable resources and references. These include online tools, worksheets, videos, and textbooks that cover square root problems comprehensively:
-
Online Worksheets and Practice Problems: Access a variety of interactive and printable worksheets to practice square root calculations.
: Offers practice problems and instructional videos.
: Printable worksheets for various levels of difficulty.
: A collection of worksheets tailored for different grades.
-
Video Tutorials: Watch video lessons to understand square roots visually and step-by-step.
: A beginner's guide to understanding square roots.
: Learn techniques for simplifying square roots.
: How to solve algebraic equations involving square roots.
-
Interactive Tools: Utilize online calculators and interactive tools to explore square roots and related concepts.
: Graph functions involving square roots and analyze their behavior.
: Explore square roots with dynamic geometry and algebra tools.
: Calculate and explore square roots with step-by-step solutions.
-
Books and Textbooks: Read in-depth explanations and practice problems from well-regarded mathematics textbooks.
Title: Algebra and Trigonometry by Michael Sullivan
Description: Covers square roots in the context of algebra and provides comprehensive practice problems.
Title: Mathematics for the International Student by Haese Mathematics
Description: Includes sections on square roots with examples and exercises.
Title: Precalculus: Mathematics for Calculus by James Stewart
Description: Offers in-depth coverage of square roots and their applications in calculus preparation.
-
Educational Websites: Explore these websites for more resources, tutorials, and interactive learning experiences.
: Detailed explanations and examples of square root problems.
: Provides an overview of square roots with interactive examples and quizzes.
: Engaging lessons and practice on square roots and radicals.
-
Apps and Games: Enhance your learning through educational apps and games that make practicing square roots fun.
: Offers square root practice and tutorials on mobile devices.
: Interactive math games including square root challenges.
: Animated educational content and quizzes on square roots.
These resources provide a comprehensive toolkit for mastering square roots, catering to various learning styles and levels. Use them to deepen your understanding and enhance your mathematical skills.
Video này giải thích về khái niệm căn bậc hai, cung cấp hướng dẫn dễ hiểu về cách tính toán và ứng dụng của chúng.
Căn Bậc Hai là gì? | Toán Học cùng Mr. J
READ MORE:
Video này cung cấp một cái nhìn toàn diện về lũy thừa và căn bậc hai, giúp người học nắm vững khái niệm và cách áp dụng chúng vào các bài toán thực tế.
Toán Học Vui - Lũy Thừa và Căn Bậc Hai