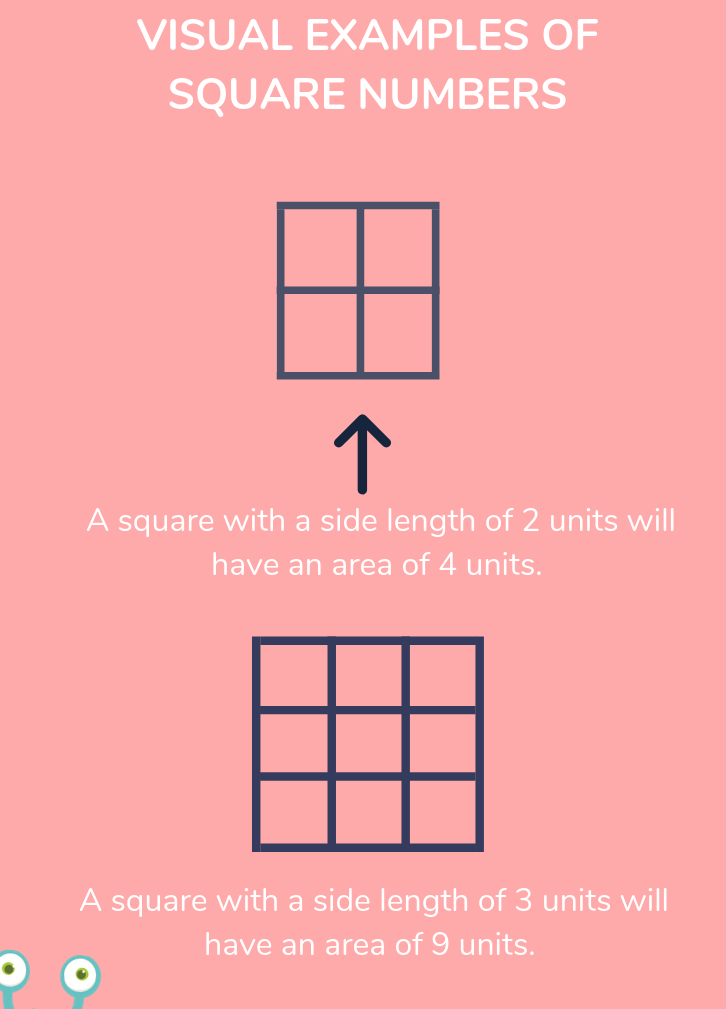Topic cube root and square root worksheet: Welcome to our comprehensive cube root and square root worksheet! Whether you're a student seeking to strengthen your math skills or a teacher looking for quality resources, this worksheet will help you master the fundamentals of cube and square roots. Dive in and enhance your understanding with practical examples and engaging practice problems.
Table of Content
- Cube Root and Square Root Worksheet
- Introduction to Square Roots
- Introduction to Cube Roots
- Properties of Square Roots
- Properties of Cube Roots
- Calculating Square Roots
- Calculating Cube Roots
- Square Roots of Perfect Squares
- Cube Roots of Perfect Cubes
- Square Roots of Non-Perfect Squares
- Cube Roots of Non-Perfect Cubes
- Applications of Square Roots
- Applications of Cube Roots
- Square Root and Cube Root Formulas
- Practice Problems on Square Roots
- Practice Problems on Cube Roots
- Answer Key for Square Root Problems
- Answer Key for Cube Root Problems
- Tips and Tricks for Square Roots
- YOUTUBE:
Cube Root and Square Root Worksheet
Welcome to our comprehensive worksheet on cube roots and square roots. This page will help you understand the concepts and provide you with practice problems to enhance your skills.
Square Root Concepts
The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). It is denoted as \( \sqrt{x} \).
- Definition: For any non-negative number \( x \), the square root of \( x \) is a number \( y \) such that \( y^2 = x \).
- Notation: The square root of \( x \) is written as \( \sqrt{x} \).
- Example: \( \sqrt{16} = 4 \) because \( 4^2 = 16 \).
Cube Root Concepts
The cube root of a number \( x \) is a number \( y \) such that \( y^3 = x \). It is denoted as \( \sqrt[3]{x} \).
- Definition: For any real number \( x \), the cube root of \( x \) is a number \( y \) such that \( y^3 = x \).
- Notation: The cube root of \( x \) is written as \( \sqrt[3]{x} \).
- Example: \( \sqrt[3]{27} = 3 \) because \( 3^3 = 27 \).
Practice Problems
Try solving these problems to test your understanding of square roots and cube roots.
- Find the square root of 25.
- Find the square root of 144.
- Find the square root of 0.25.
- Find the cube root of 64.
- Find the cube root of 125.
- Find the cube root of 0.008.
Solutions
Check your answers with the solutions provided below:
| 1. \( \sqrt{25} \) | 5 |
| 2. \( \sqrt{144} \) | 12 |
| 3. \( \sqrt{0.25} \) | 0.5 |
| 4. \( \sqrt[3]{64} \) | 4 |
| 5. \( \sqrt[3]{125} \) | 5 |
| 6. \( \sqrt[3]{0.008} \) | 0.2 |
We hope this worksheet helps you grasp the concepts of square roots and cube roots. Keep practicing to improve your skills!

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. Square roots are fundamental in various branches of mathematics and are denoted by the radical symbol \( \sqrt{} \).
Here are some key points about square roots:
- Definition: The square root of \( x \) is a number \( y \) such that \( y^2 = x \).
- Notation: The square root of \( x \) is written as \( \sqrt{x} \).
- Principal Square Root: For non-negative numbers, the principal square root is the non-negative root.
Understanding square roots involves recognizing perfect squares and calculating non-perfect squares. Below are examples to illustrate these concepts:
| Number | Square Root | Explanation |
| 4 | \( \sqrt{4} = 2 \) | Because \( 2 \times 2 = 4 \) |
| 9 | \( \sqrt{9} = 3 \) | Because \( 3 \times 3 = 9 \) |
| 16 | \( \sqrt{16} = 4 \) | Because \( 4 \times 4 = 16 \) |
| 2 | \( \sqrt{2} \approx 1.414 \) | 1.414 is an approximation as the square root of 2 is an irrational number. |
To calculate square roots of non-perfect squares, you can use methods such as estimation, prime factorization, or a calculator for more precise results. Practicing these calculations helps in understanding the concept better and enhances your mathematical skills.
Introduction to Cube Roots
The cube root of a number is a value that, when multiplied by itself twice, gives the original number. Cube roots are essential in various mathematical applications and are denoted by the radical symbol with an index of three, \( \sqrt[3]{} \).
Here are some key points about cube roots:
- Definition: The cube root of \( x \) is a number \( y \) such that \( y^3 = x \).
- Notation: The cube root of \( x \) is written as \( \sqrt[3]{x} \).
- Real and Complex Roots: Every real number has exactly one real cube root and two complex conjugate roots.
Understanding cube roots involves recognizing perfect cubes and calculating non-perfect cubes. Below are examples to illustrate these concepts:
| Number | Cube Root | Explanation |
| 8 | \( \sqrt[3]{8} = 2 \) | Because \( 2 \times 2 \times 2 = 8 \) |
| 27 | \( \sqrt[3]{27} = 3 \) | Because \( 3 \times 3 \times 3 = 27 \) |
| 64 | \( \sqrt[3]{64} = 4 \) | Because \( 4 \times 4 \times 4 = 64 \) |
| 2 | \( \sqrt[3]{2} \approx 1.26 \) | 1.26 is an approximation as the cube root of 2 is an irrational number. |
To calculate cube roots of non-perfect cubes, you can use methods such as estimation, prime factorization, or a calculator for more precise results. Practicing these calculations helps in understanding the concept better and enhances your mathematical skills.
Properties of Square Roots
Square roots have several important properties that are useful in various mathematical calculations and problem-solving scenarios. Understanding these properties can help simplify complex expressions and solve equations more efficiently.
- Non-negativity: For any non-negative number \( x \), the square root \( \sqrt{x} \) is also non-negative. This is because a negative number squared results in a positive number, making the square root of a positive number always positive.
- Product Property: The square root of a product is equal to the product of the square roots of the factors. Mathematically, this is expressed as: \[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \] for any non-negative numbers \( a \) and \( b \).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. This property is expressed as: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \] for any non-negative numbers \( a \) and \( b \) where \( b \neq 0 \).
- Square of a Square Root: The square of the square root of a number returns the original number: \[ (\sqrt{x})^2 = x \] for any non-negative number \( x \).
- Sum and Difference: The square root of a sum or difference does not equal the sum or difference of the square roots. For example: \[ \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \] \[ \sqrt{a - b} \neq \sqrt{a} - \sqrt{b} \] These equalities hold true only in specific cases, such as when \( b = 0 \).
Here are some examples to illustrate these properties:
| Property | Example | Explanation |
| Product Property | \( \sqrt{36 \cdot 25} = \sqrt{36} \cdot \sqrt{25} = 6 \cdot 5 = 30 \) | The square root of the product equals the product of the square roots. |
| Quotient Property | \( \sqrt{\frac{49}{16}} = \frac{\sqrt{49}}{\sqrt{16}} = \frac{7}{4} \) | The square root of the quotient equals the quotient of the square roots. |
| Square of a Square Root | \( (\sqrt{9})^2 = 9 \) | The square of the square root returns the original number. |
Understanding and applying these properties can greatly enhance your ability to work with square roots and solve various mathematical problems.
Properties of Cube Roots
Cube roots have several important properties that are useful in various mathematical calculations and problem-solving scenarios. Understanding these properties can help simplify complex expressions and solve equations more efficiently.
- Sign Preservation: The cube root of a positive number is positive, and the cube root of a negative number is negative. For any real number \( x \): \[ \sqrt[3]{x} \geq 0 \quad \text{if and only if} \quad x \geq 0 \] \[ \sqrt[3]{x} < 0 \quad \text{if and only if} \quad x < 0 \]
- Product Property: The cube root of a product is equal to the product of the cube roots of the factors. Mathematically, this is expressed as: \[ \sqrt[3]{a \cdot b} = \sqrt[3]{a} \cdot \sqrt[3]{b} \] for any real numbers \( a \) and \( b \).
- Quotient Property: The cube root of a quotient is equal to the quotient of the cube roots of the numerator and the denominator. This property is expressed as: \[ \sqrt[3]{\frac{a}{b}} = \frac{\sqrt[3]{a}}{\sqrt[3]{b}} \] for any real numbers \( a \) and \( b \) where \( b \neq 0 \).
- Cube of a Cube Root: The cube of the cube root of a number returns the original number: \[ (\sqrt[3]{x})^3 = x \] for any real number \( x \).
- Sum and Difference: The cube root of a sum or difference does not equal the sum or difference of the cube roots. For example: \[ \sqrt[3]{a + b} \neq \sqrt[3]{a} + \sqrt[3]{b} \] \[ \sqrt[3]{a - b} \neq \sqrt[3]{a} - \sqrt[3]{b} \] These equalities hold true only in specific cases, such as when \( b = 0 \).
Here are some examples to illustrate these properties:
| Property | Example | Explanation |
| Product Property | \( \sqrt[3]{8 \cdot 27} = \sqrt[3]{8} \cdot \sqrt[3]{27} = 2 \cdot 3 = 6 \) | The cube root of the product equals the product of the cube roots. |
| Quotient Property | \( \sqrt[3]{\frac{64}{8}} = \frac{\sqrt[3]{64}}{\sqrt[3]{8}} = \frac{4}{2} = 2 \) | The cube root of the quotient equals the quotient of the cube roots. |
| Cube of a Cube Root | \( (\sqrt[3]{27})^3 = 27 \) | The cube of the cube root returns the original number. |
Understanding and applying these properties can greatly enhance your ability to work with cube roots and solve various mathematical problems.

Calculating Square Roots
Calculating square roots can be done using various methods, including prime factorization, estimation, and using a calculator. Here, we will discuss these methods in detail to help you understand and apply them effectively.
Prime Factorization Method
This method involves breaking down a number into its prime factors and then pairing the factors to find the square root.
- Write the number as a product of its prime factors.
- Pair the prime factors.
- Take one number from each pair and multiply them together to get the square root.
Example:
Find the square root of 144:
- Prime factorization of 144: \( 144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3 \)
- Pair the factors: \( (2 \times 2) \times (2 \times 2) \times (3 \times 3) \)
- Take one number from each pair: \( 2 \times 2 \times 3 = 12 \)
Thus, \( \sqrt{144} = 12 \).
Estimation Method
When a number is not a perfect square, you can estimate the square root by finding the two closest perfect squares between which the number lies.
- Identify the two perfect squares closest to the given number.
- Estimate the square root to be between the square roots of these two perfect squares.
- Refine your estimate by using averages or a calculator for more precision.
Example:
Estimate the square root of 50:
- Identify the closest perfect squares: 49 (\( 7^2 \)) and 64 (\( 8^2 \))
- Estimate: \( 7 < \sqrt{50} < 8 \)
- Refine: Since 50 is closer to 49, we can estimate \( \sqrt{50} \approx 7.1 \)
Using a Calculator
Using a calculator is the quickest method for finding the square root of any number.
- Enter the number into the calculator.
- Press the square root (√) button.
- Read the result displayed on the calculator.
Example:
Find the square root of 200 using a calculator:
- Enter 200.
- Press √.
- Result: \( \sqrt{200} \approx 14.14 \).
These methods will help you calculate square roots effectively, whether you are dealing with perfect squares or estimating non-perfect squares.
Calculating Cube Roots
Calculating cube roots can be done using various methods, including prime factorization, estimation, and using a calculator. Here, we will discuss these methods in detail to help you understand and apply them effectively.
Prime Factorization Method
This method involves breaking down a number into its prime factors and then grouping the factors in sets of three to find the cube root.
- Write the number as a product of its prime factors.
- Group the prime factors in sets of three.
- Take one number from each group and multiply them together to get the cube root.
Example:
Find the cube root of 216:
- Prime factorization of 216: \( 216 = 2 \times 2 \times 2 \times 3 \times 3 \times 3 \)
- Group the factors: \( (2 \times 2 \times 2) \times (3 \times 3 \times 3) \)
- Take one number from each group: \( 2 \times 3 = 6 \)
Thus, \( \sqrt[3]{216} = 6 \).
Estimation Method
When a number is not a perfect cube, you can estimate the cube root by finding the two closest perfect cubes between which the number lies.
- Identify the two perfect cubes closest to the given number.
- Estimate the cube root to be between the cube roots of these two perfect cubes.
- Refine your estimate by using averages or a calculator for more precision.
Example:
Estimate the cube root of 50:
- Identify the closest perfect cubes: 27 (\( 3^3 \)) and 64 (\( 4^3 \))
- Estimate: \( 3 < \sqrt[3]{50} < 4 \)
- Refine: Since 50 is closer to 64, we can estimate \( \sqrt[3]{50} \approx 3.7 \)
Using a Calculator
Using a calculator is the quickest method for finding the cube root of any number.
- Enter the number into the calculator.
- Press the cube root (∛) button or use the exponent key with \( \frac{1}{3} \).
- Read the result displayed on the calculator.
Example:
Find the cube root of 200 using a calculator:
- Enter 200.
- Press ∛ or enter \( 200^{\frac{1}{3}} \).
- Result: \( \sqrt[3]{200} \approx 5.85 \).
These methods will help you calculate cube roots effectively, whether you are dealing with perfect cubes or estimating non-perfect cubes.
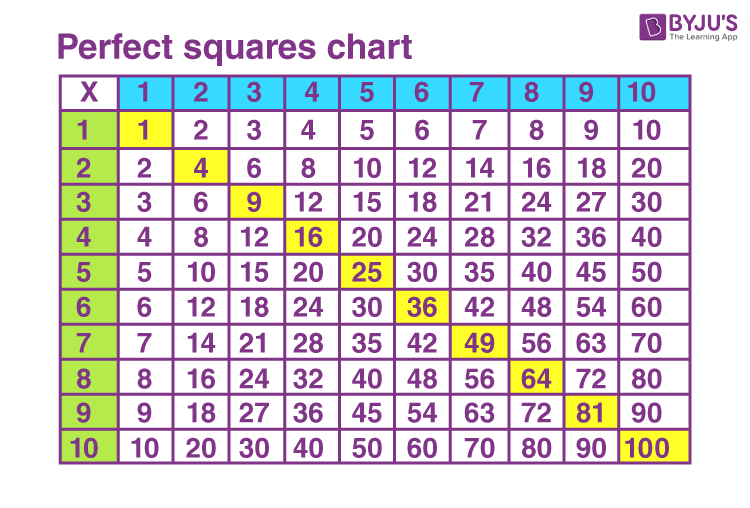
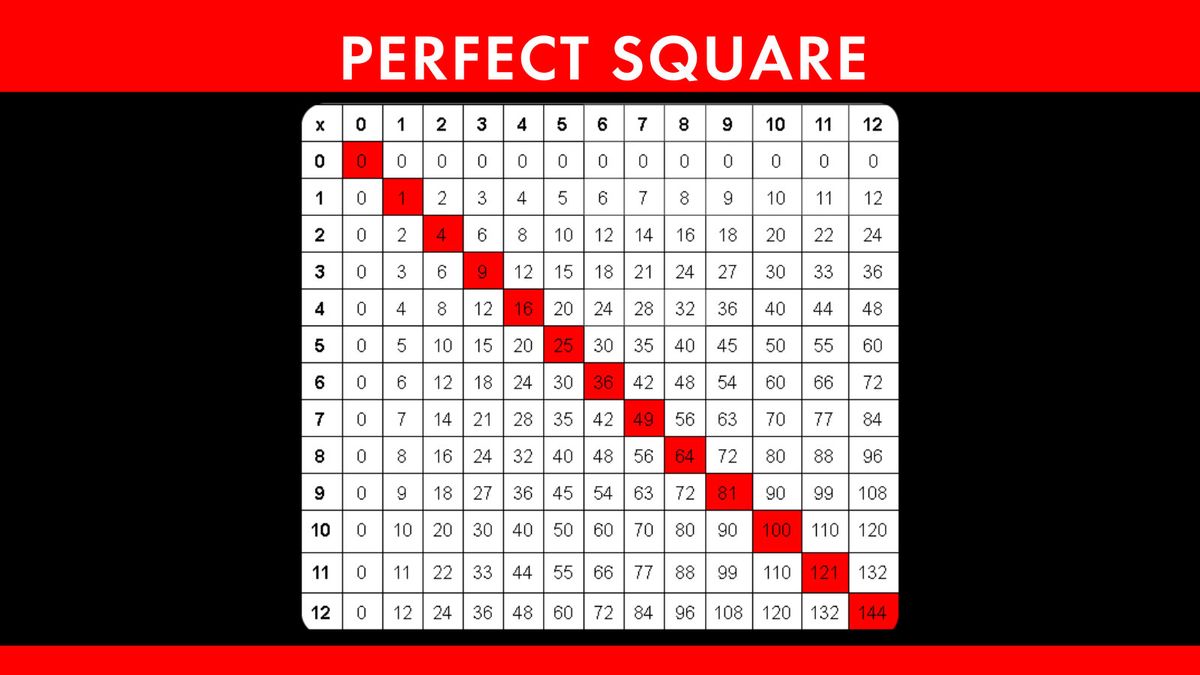
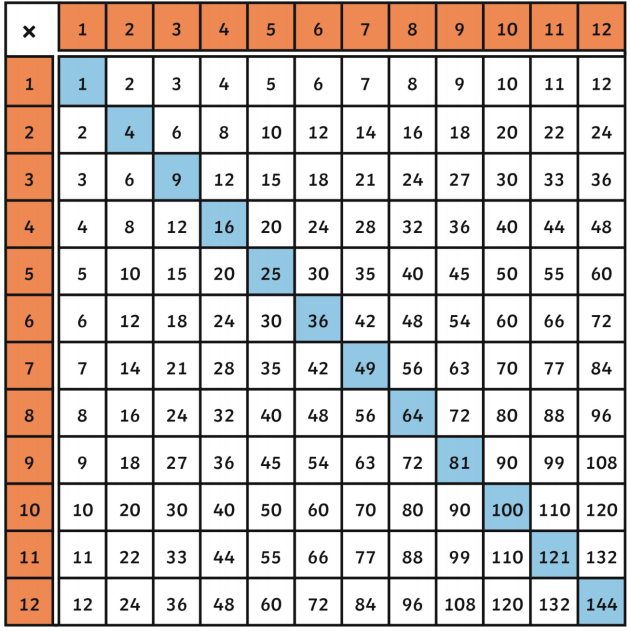
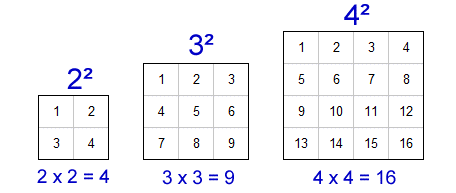
Square Roots of Perfect Squares
Perfect squares are numbers that are the square of an integer. Finding the square roots of perfect squares is straightforward because the result is always an integer. Here, we will discuss the concept of perfect squares and how to calculate their square roots step by step.
Definition of Perfect Squares
A perfect square is a number that can be expressed as the product of an integer with itself. For example, 1, 4, 9, 16, 25, and so on are perfect squares because they can be written as:
- 1 = \(1 \times 1\)
- 4 = \(2 \times 2\)
- 9 = \(3 \times 3\)
- 16 = \(4 \times 4\)
- 25 = \(5 \times 5\)
Calculating Square Roots of Perfect Squares
To find the square root of a perfect square, follow these steps:
- Identify the perfect square.
- Determine the integer that, when multiplied by itself, gives the perfect square.
Let's go through some examples to illustrate this process:
| Perfect Square | Square Root | Explanation |
| 64 | 8 | \(8 \times 8 = 64\) |
| 121 | 11 | \(11 \times 11 = 121\) |
| 144 | 12 | \(12 \times 12 = 144\) |
| 169 | 13 | \(13 \times 13 = 169\) |
| 196 | 14 | \(14 \times 14 = 196\) |
Recognizing Perfect Squares
Being able to recognize perfect squares can help in quickly determining their square roots. Here is a list of perfect squares from 1 to 20:
- 1 (\(1^2\))
- 4 (\(2^2\))
- 9 (\(3^2\))
- 16 (\(4^2\))
- 25 (\(5^2\))
- 36 (\(6^2\))
- 49 (\(7^2\))
- 64 (\(8^2\))
- 81 (\(9^2\))
- 100 (\(10^2\))
- 121 (\(11^2\))
- 144 (\(12^2\))
- 169 (\(13^2\))
- 196 (\(14^2\))
- 225 (\(15^2\))
- 256 (\(16^2\))
- 289 (\(17^2\))
- 324 (\(18^2\))
- 361 (\(19^2\))
- 400 (\(20^2\))
Understanding and recognizing perfect squares simplifies the process of finding their square roots and enhances your mathematical skills.
Cube Roots of Perfect Cubes
A perfect cube is a number that can be expressed as the product of an integer multiplied by itself three times. When finding the cube root of a perfect cube, we are looking for the number that, when multiplied by itself three times, gives the perfect cube.
To find the cube root of a perfect cube, we can use prime factorization. First, we need to express the given number as the product of prime factors. Then, we group the prime factors into triples, each representing one set of the number's factors. Finally, we take one factor from each group and multiply them together to find the cube root.
Let's illustrate this with an example:
Consider the perfect cube 64.
- Prime factorize 64: \(64 = 2^6\).
- Group the prime factors into triples: \(2^2 \times 2^2 \times 2^2\).
- Take one factor from each group and multiply them together: \(2 \times 2 \times 2 = 8\).
Therefore, the cube root of 64 is 8.
Here are a few more examples:
- For \(125 = 5^3\): \( \sqrt[3]{125} = 5 \).
- For \(216 = 6^3\): \( \sqrt[3]{216} = 6 \).
- For \(729 = 9^3\): \( \sqrt[3]{729} = 9 \).
It's important to remember that the cube root of a perfect cube is always an integer.

Square Roots of Non-Perfect Squares
A non-perfect square is a number that cannot be expressed as the product of an integer multiplied by itself. When finding the square root of a non-perfect square, we are looking for an approximation of the square root since it won't be a whole number.
One method to find the square root of a non-perfect square is by using the long division method or the digit by digit method. Both methods involve iterative calculations to approximate the square root.
Let's demonstrate this with an example using the long division method:
Consider finding the square root of 15.
- Start by grouping the digits into pairs, starting from the decimal point if necessary. In this case, 15 is just one digit, so it's grouped as 15.00.
- Find the largest integer whose square is less than or equal to the leftmost group. In this case, \(3^2 = 9\), so the largest integer is 3.
- Subtract the square of this integer from the leftmost group, and bring down the next pair of digits.
- Double the root obtained so far and write it as the divisor. Guess the largest digit for the quotient that, when added as a suffix to the divisor, yields a product less than or equal to the number obtained by bringing down the next pair of digits.
- Divide and continue this process until the desired level of accuracy is achieved.
Using this method, we find that \( \sqrt{15} \approx 3.87298\).
Similarly, the digit by digit method involves finding the square root digit by digit, starting from the leftmost digit.
It's important to note that the square root of a non-perfect square will be an irrational number and can be represented as a decimal with infinite non-repeating digits.
Cube Roots of Non-Perfect Cubes
A non-perfect cube is a number that cannot be expressed as the product of an integer multiplied by itself three times. Finding the cube root of a non-perfect cube involves approximating the cube root since it won't be an integer.
One method to find the cube root of a non-perfect cube is by using estimation and iteration. This involves guessing a number, cubing it, and comparing the result to the given number to refine the guess.
Let's illustrate this method with an example:
Consider finding the cube root of 10.
- Start with an initial guess. Let's start with 2.
- Cube the guess: \(2^3 = 8\).
- Compare the result to the given number. Since 8 is less than 10, we need to increase our guess.
- Adjust the guess accordingly. Let's try 3.
- Cube the new guess: \(3^3 = 27\).
- Compare the result to the given number. Since 27 is greater than 10, we need to decrease our guess.
- Refine the guess further using techniques like bisection method or Newton's method until the desired level of accuracy is achieved.
Using this method, we find that \( \sqrt[3]{10} \approx 2.15443\).
Another approach to find the cube root of a non-perfect cube is by using approximation formulas or algorithms such as the Newton-Raphson method.
It's important to note that the cube root of a non-perfect cube will be an irrational number and can be represented as a decimal with infinite non-repeating digits.
Applications of Square Roots
Square roots have numerous applications in various fields such as mathematics, physics, engineering, and real life. Understanding how to apply square roots can help solve many practical problems. Here are some key applications:
- Geometry and Area Calculations:
Square roots are used to determine the side length of a square when the area is known. For example, if the area of a square is 25 square units, the side length is the square root of 25, which is 5 units.
Using the formula \( \text{Side length} = \sqrt{\text{Area}} \), you can easily find the dimensions of a square or solve problems involving areas.
- Pythagorean Theorem:
In a right-angled triangle, the square root is used to find the length of the hypotenuse or one of the legs. The theorem is given by \( a^2 + b^2 = c^2 \), where \( c \) is the hypotenuse. To find \( c \), you use \( c = \sqrt{a^2 + b^2} \).
- Physics and Engineering:
Square roots are often used in formulas involving areas, volumes, and other physical properties. For example, in calculating the RMS (root mean square) value in electrical engineering, square roots are essential.
Another application is in the determination of the standard deviation in statistics, which involves taking the square root of the variance.
- Finance:
Square roots are used in financial calculations, such as determining the volatility of stock prices. The standard deviation, which measures volatility, involves square roots.
- Quadratic Equations:
Solving quadratic equations often requires taking the square root of a number. The quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) involves finding the square root of the discriminant.
Let's explore a few detailed examples to illustrate these applications:
Example 1: Geometry
Find the side length of a square with an area of 64 square units.
- Start with the area formula: \( \text{Area} = \text{Side length}^2 \).
- Substitute the given area: \( 64 = \text{Side length}^2 \).
- Take the square root of both sides: \( \sqrt{64} = \text{Side length} \).
- Therefore, the side length is 8 units.
Example 2: Pythagorean Theorem
Find the hypotenuse of a right-angled triangle with legs of 3 units and 4 units.
- Use the Pythagorean theorem: \( a^2 + b^2 = c^2 \).
- Substitute the given lengths: \( 3^2 + 4^2 = c^2 \).
- Calculate the squares: \( 9 + 16 = c^2 \).
- Simplify: \( 25 = c^2 \).
- Take the square root of both sides: \( c = \sqrt{25} \).
- Therefore, the hypotenuse is 5 units.
Example 3: Finance
Calculate the standard deviation of a dataset where the variance is 16.
- Start with the variance formula: \( \text{Variance} = \sigma^2 \).
- Substitute the given variance: \( 16 = \sigma^2 \).
- Take the square root of both sides: \( \sigma = \sqrt{16} \).
- Therefore, the standard deviation is 4.
Applications of Cube Roots
Cube roots have a variety of practical applications in different fields such as geometry, physics, engineering, and everyday problem solving. Understanding how to apply cube roots can be very useful in solving many types of problems. Here are some important applications:
- Volume Calculations:
Cube roots are used to determine the side length of a cube when the volume is known. For example, if the volume of a cube is 27 cubic units, the side length is the cube root of 27, which is 3 units.
Using the formula \( \text{Side length} = \sqrt[3]{\text{Volume}} \), you can easily find the dimensions of a cube or solve problems involving volumes.
- Engineering and Design:
Cube roots are often used in engineering to determine the scaling of three-dimensional models. For example, when scaling a model up or down, knowing the cube root helps maintain the proportions of volume and dimensions.
- Physics:
In physics, cube roots can be used to calculate quantities like the mean free path of particles or the density of a substance. For instance, the density of a substance is inversely proportional to the cube root of its volume.
- Economics:
In economics, the cube root function can be applied to calculate compound interest, growth rates, and other financial metrics that involve exponential growth over three periods.
- Geometry:
Cube roots are used to solve geometric problems involving cubes and other three-dimensional shapes. They help in finding dimensions, surface areas, and other properties based on volume.
Let's explore a few detailed examples to illustrate these applications:
Example 1: Volume Calculation
Find the side length of a cube with a volume of 125 cubic units.
- Start with the volume formula: \( \text{Volume} = \text{Side length}^3 \).
- Substitute the given volume: \( 125 = \text{Side length}^3 \).
- Take the cube root of both sides: \( \sqrt[3]{125} = \text{Side length} \).
- Therefore, the side length is 5 units.
Example 2: Engineering Scaling
If a model is scaled up by a factor of 8, what is the scaling factor for the dimensions?
- Understand that volume scaling factor = 8.
- Since \( \text{Volume scaling factor} = (\text{Dimension scaling factor})^3 \), we need to find the cube root of 8.
- Calculate the cube root: \( \text{Dimension scaling factor} = \sqrt[3]{8} \).
- Therefore, the dimension scaling factor is 2.
Example 3: Physics Calculation
Determine the density of a substance if its volume is increased by a factor of 27 and its original density is 1.5 g/cm3.
- Understand that volume increased by a factor of 27 means \( \text{New volume} = 27 \times \text{Original volume} \).
- Density is inversely proportional to the volume: \( \text{New density} = \frac{\text{Original density}}{\sqrt[3]{27}} \).
- Calculate the cube root: \( \sqrt[3]{27} = 3 \).
- Calculate the new density: \( \text{New density} = \frac{1.5}{3} = 0.5 \) g/cm3.

Square Root and Cube Root Formulas
Understanding the formulas for calculating square roots and cube roots is essential in various mathematical and practical applications. Below are the detailed formulas and methods for both square roots and cube roots:
Square Root Formulas
The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). Here are some common formulas and properties related to square roots:
- Basic Square Root Formula:
\( \sqrt{x} = y \) where \( y^2 = x \).
- Square Root of a Product:
\( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \).
- Square Root of a Quotient:
\( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Square Root of a Power:
\( \sqrt{a^2} = |a| \).
- Rationalizing Denominators:
\( \frac{1}{\sqrt{a}} = \frac{\sqrt{a}}{a} \).
Examples of Square Root Calculations
- Calculate \( \sqrt{49} \):
- \( \sqrt{49} = 7 \) because \( 7^2 = 49 \).
- Calculate \( \sqrt{9 \times 16} \):
- \( \sqrt{9 \times 16} = \sqrt{9} \times \sqrt{16} = 3 \times 4 = 12 \).
- Calculate \( \sqrt{\frac{25}{4}} \):
- \( \sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2} \).
Cube Root Formulas
The cube root of a number \( x \) is a value \( y \) such that \( y^3 = x \). Here are some common formulas and properties related to cube roots:
- Basic Cube Root Formula:
\( \sqrt[3]{x} = y \) where \( y^3 = x \).
- Cube Root of a Product:
\( \sqrt[3]{ab} = \sqrt[3]{a} \times \sqrt[3]{b} \).
- Cube Root of a Quotient:
\( \sqrt[3]{\frac{a}{b}} = \frac{\sqrt[3]{a}}{\sqrt[3]{b}} \).
- Cube Root of a Power:
\( \sqrt[3]{a^3} = a \).
Examples of Cube Root Calculations
- Calculate \( \sqrt[3]{27} \):
- \( \sqrt[3]{27} = 3 \) because \( 3^3 = 27 \).
- Calculate \( \sqrt[3]{8 \times 64} \):
- \( \sqrt[3]{8 \times 64} = \sqrt[3]{8} \times \sqrt[3]{64} = 2 \times 4 = 8 \).
- Calculate \( \sqrt[3]{\frac{125}{27}} \):
- \( \sqrt[3]{\frac{125}{27}} = \frac{\sqrt[3]{125}}{\sqrt[3]{27}} = \frac{5}{3} \).
Practice Problems on Square Roots
Practicing square root problems can help reinforce your understanding of the concept and its applications. Here are some practice problems, ranging from basic to advanced, to help you master square roots:
Basic Problems
- Find the square root of 49.
- Calculate \( \sqrt{64} \).
- Determine \( \sqrt{81} \).
- What is \( \sqrt{100} \)?
- Find \( \sqrt{144} \).
Intermediate Problems
- Simplify \( \sqrt{50} \).
- Calculate \( \sqrt{75} \).
- Determine \( \sqrt{98} \).
- What is \( \sqrt{125} \)?
- Find \( \sqrt{200} \).
Advanced Problems
- Find \( \sqrt{324} \).
- Calculate \( \sqrt{484} \).
- Determine \( \sqrt{625} \).
- What is \( \sqrt{729} \)?
- Find \( \sqrt{900} \).
Application Problems
Use square roots to solve these practical problems:
- A square garden has an area of 225 square meters. What is the length of each side of the garden?
- The area of a square painting is 400 square centimeters. Calculate the length of one side of the painting.
- If the area of a square field is 1024 square meters, determine the side length of the field.
- A square table has an area of 289 square inches. What is the length of one side of the table?
- The area of a square room is 576 square feet. Calculate the length of each side of the room.
Challenge Problems
Test your skills with these challenging square root problems:
- Simplify \( \sqrt{450} \) to its simplest radical form.
- Calculate \( \sqrt{2^6 \times 3^2} \).
- Determine the length of the diagonal of a square with a side length of 15 cm.
- If \( \sqrt{a} = 7 \), find the value of \( a \).
- Express \( \sqrt{72} \) in simplest radical form.
Practice Problems on Cube Roots
Practicing cube root problems can help reinforce your understanding of the concept and its applications. Here are some practice problems, ranging from basic to advanced, to help you master cube roots:
Basic Problems
- Find the cube root of 8.
- Calculate \( \sqrt[3]{27} \).
- Determine \( \sqrt[3]{64} \).
- What is \( \sqrt[3]{125} \)?
- Find \( \sqrt[3]{216} \).
Intermediate Problems
- Simplify \( \sqrt[3]{32} \).
- Calculate \( \sqrt[3]{81} \).
- Determine \( \sqrt[3]{243} \).
- What is \( \sqrt[3]{512} \)?
- Find \( \sqrt[3]{1000} \).
Advanced Problems
- Find \( \sqrt[3]{1331} \).
- Calculate \( \sqrt[3]{1728} \).
- Determine \( \sqrt[3]{2197} \).
- What is \( \sqrt[3]{2744} \)?
- Find \( \sqrt[3]{3375} \).
Application Problems
Use cube roots to solve these practical problems:
- A cube-shaped box has a volume of 343 cubic meters. What is the length of each side of the box?
- The volume of a cube is 512 cubic centimeters. Calculate the length of one side of the cube.
- If the volume of a cube is 1331 cubic meters, determine the side length of the cube.
- A cube has a volume of 8000 cubic inches. What is the length of one side of the cube?
- The volume of a cube is 2744 cubic feet. Calculate the length of each side of the cube.
Challenge Problems
Test your skills with these challenging cube root problems:
- Simplify \( \sqrt[3]{3375} \) to its simplest form.
- Calculate \( \sqrt[3]{2^9 \times 3^3} \).
- Determine the side length of a cube with a volume of 5832 cm³.
- If \( \sqrt[3]{a} = 9 \), find the value of \( a \).
- Express \( \sqrt[3]{1728} \) in simplest form.
Answer Key for Square Root Problems
Below are the detailed solutions to the practice problems on square roots:
Basic Problems
- \( \sqrt{49} = 7 \)
- \( \sqrt{64} = 8 \)
- \( \sqrt{81} = 9 \)
- \( \sqrt{100} = 10 \)
- \( \sqrt{144} = 12 \)
Intermediate Problems
- \( \sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2} \)
- \( \sqrt{75} = \sqrt{25 \times 3} = 5\sqrt{3} \)
- \( \sqrt{98} = \sqrt{49 \times 2} = 7\sqrt{2} \)
- \( \sqrt{125} = \sqrt{25 \times 5} = 5\sqrt{5} \)
- \( \sqrt{200} = \sqrt{100 \times 2} = 10\sqrt{2} \)
Advanced Problems
- \( \sqrt{324} = 18 \)
- \( \sqrt{484} = 22 \)
- \( \sqrt{625} = 25 \)
- \( \sqrt{729} = 27 \)
- \( \sqrt{900} = 30 \)
Application Problems
- The side length of a square garden with an area of 225 square meters is \( \sqrt{225} = 15 \) meters.
- The side length of a square painting with an area of 400 square centimeters is \( \sqrt{400} = 20 \) centimeters.
- The side length of a square field with an area of 1024 square meters is \( \sqrt{1024} = 32 \) meters.
- The side length of a square table with an area of 289 square inches is \( \sqrt{289} = 17 \) inches.
- The side length of a square room with an area of 576 square feet is \( \sqrt{576} = 24 \) feet.
Challenge Problems
- \( \sqrt{450} = \sqrt{25 \times 18} = 5\sqrt{18} = 5 \times 3\sqrt{2} = 15\sqrt{2} \)
- \( \sqrt{2^6 \times 3^2} = \sqrt{64 \times 9} = \sqrt{576} = 24 \)
- The diagonal of a square with a side length of 15 cm is \( \sqrt{15^2 + 15^2} = \sqrt{450} = 15\sqrt{2} \) cm.
- If \( \sqrt{a} = 7 \), then \( a = 7^2 = 49 \).
- \( \sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2} \)

Answer Key for Cube Root Problems
Here are the answers to the cube root problems given in the worksheet. Each solution is detailed step by step for better understanding.
Example Problems and Solutions
-
Problem: Find the cube root of 64.
Solution:
- Write 64.
- Find the prime factors of 64: \( 64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \).
- Group the factors in sets of three: \( (2 \times 2 \times 2) \times (2 \times 2 \times 2) \).
- Take one factor from each group and multiply them together: \( 2 \times 2 = 4 \).
- The cube root of 64 is 4.
-
Problem: Find the cube root of 125.
Solution:
- Write 125.
- Find the prime factors of 125: \( 125 = 5 \times 5 \times 5 \).
- Group the factors in sets of three: \( (5 \times 5 \times 5) \).
- Take one factor from the group: 5.
- The cube root of 125 is 5.
-
Problem: Find the cube root of 27.
Solution:
- Write 27.
- Find the prime factors of 27: \( 27 = 3 \times 3 \times 3 \).
- Group the factors in sets of three: \( (3 \times 3 \times 3) \).
- Take one factor from the group: 3.
- The cube root of 27 is 3.
Cube Roots of Non-Perfect Cubes
-
Problem: Estimate the cube root of 37.
Solution:
- Round 37 to the nearest perfect cube, which is 27.
- The cube root of 27 is 3.
- Adjust the result using the estimation method: \( (3/3) \times 37 = 37 \).
- The estimated cube root of 37 is approximately 3.3.
Advanced Problems
-
Problem: Find the cube root of 216.
Solution:
- Write 216.
- Find the prime factors of 216: \( 216 = 2 \times 2 \times 2 \times 3 \times 3 \times 3 \).
- Group the factors in sets of three: \( (2 \times 2 \times 2) \times (3 \times 3 \times 3) \).
- Take one factor from each group and multiply them together: \( 2 \times 3 = 6 \).
- The cube root of 216 is 6.
Tips and Tricks for Square Roots
Finding square roots can be simplified with some handy tips and tricks. Here are several methods to make the process easier and quicker:
1. Memorize Perfect Squares
Knowing the squares of numbers from 1 to 20 can significantly speed up calculations. Here are a few to remember:
- \(1^2 = 1\)
- \(2^2 = 4\)
- \(3^2 = 9\)
- \(4^2 = 16\)
- \(5^2 = 25\)
- \(6^2 = 36\)
- \(7^2 = 49\)
- \(8^2 = 64\)
- \(9^2 = 81\)
- \(10^2 = 100\)
2. Identify Close Perfect Squares
When you need to find the square root of a number that is not a perfect square, identify the nearest perfect squares and estimate:
- For \( \sqrt{50} \), since \( \sqrt{49} = 7 \) and \( \sqrt{64} = 8 \), the square root of 50 is slightly more than 7.
- For \( \sqrt{90} \), since \( \sqrt{81} = 9 \) and \( \sqrt{100} = 10 \), the square root of 90 is slightly less than 10.
3. Use Prime Factorization
Decompose the number into its prime factors and group them to find the square root:
Example: \( \sqrt{144} \)
- Prime factorize 144: \( 144 = 2^4 \times 3^2 \)
- Group the factors into pairs: \( (2^2)^2 \times (3^1)^2 \)
- Take one number from each pair: \( 2^2 \times 3 = 4 \times 3 = 12 \)
- Therefore, \( \sqrt{144} = 12 \).
4. Simplify with Estimation for Non-Perfect Squares
Break down the number into smaller components and estimate:
Example: \( \sqrt{52} \)
- Approximate \( \sqrt{52} \) between \( \sqrt{49} = 7 \) and \( \sqrt{64} = 8 \).
- Refine your estimate: \( 52 \) is closer to \( 49 \), so try \( 7.2 \) or \( 7.3 \).
5. Use Long Division Method
Apply the long division method to find precise square roots for larger numbers:
- Pair the digits from right to left.
- Find the largest number whose square is less than or equal to the first set of digits.
- Subtract and bring down the next pair of digits.
- Repeat the process until all digit pairs are used.
6. Square Root by Subtraction
Subtract consecutive odd numbers starting from the given number until you reach zero:
Example: \( \sqrt{25} \)
- 25 - 1 = 24
- 24 - 3 = 21
- 21 - 5 = 16
- 16 - 7 = 9
- 9 - 9 = 0
Since it took 5 steps, \( \sqrt{25} = 5 \).
7. Utilize Calculators or Math Software
For complex calculations, use a scientific calculator or math software to find square roots quickly and accurately.
By mastering these techniques, you can efficiently find square roots and apply them in various mathematical problems.
Căn Bậc Hai và Căn Bậc Ba | Toán với Thầy J
READ MORE:
Căn Bậc Hai Là Gì? | Toán với Thầy J