Topic square root equations worksheet: Discover the essential techniques to solve square root equations with our comprehensive worksheet. This guide is designed to enhance your understanding and proficiency in algebra, providing step-by-step instructions and practice problems to build your confidence and skills. Perfect for students and educators alike, this worksheet is your key to mastering square root equations.
Table of Content
- Square Root Equations Worksheet
- Introduction to Square Root Equations
- Understanding Square Roots
- Basic Square Root Equations
- Advanced Square Root Equations
- Solving Techniques for Square Root Equations
- Common Mistakes and Tips
- Square Root Equations in Word Problems
- Applications of Square Root Equations
- Practice Worksheets
- Answer Keys
- YOUTUBE:
Square Root Equations Worksheet
Square root equations are fundamental in algebra and help students understand the principles of solving equations involving square roots. Below are some detailed resources and examples of problems related to square root equations.
Worksheet Resources
-
Easy Teacher Worksheets
This series of worksheets provides practice in solving square root equations and converting word problems into equations. Students can practice and check their answers with provided answer keys.
- Completing the Square - Lesson
- Worksheet 1: Solve equations like \(x^2 + 2x - 10 = 0\)
- Worksheet 2: Solve equations like \(x^2 - 6x - 9 = 0\)
- Completing the Square - Review and Quiz
-
Math-Aids Worksheets
These worksheets focus on solving square root equations and include various algebra topics such as radical functions and quadratic functions.
- Solving Quadratic Equations by Taking Square Roots
- Understanding Radical Functions
- Function Tables and Graphing
-
Math Worksheets 4 Kids
Printable worksheets for practicing square root calculations, factorization, and long division methods. These are ideal for reinforcing students' understanding of square roots.
- Square Root Calculation Worksheets
- Solving Equations with Square Roots
- Pythagorean Theorem Applications
Example Problems
Here are some example problems that can be found in the worksheets:
- Solve for \(x\): \(\sqrt{x + 3} = 5\)
- Solve for \(y\): \(y^2 - 4 = 0\)
- Convert to an equation and solve: "The square root of a number increased by 7 is 10."
Understanding Square Root Equations
To solve square root equations, follow these steps:
- Isolate the square root expression.
- Square both sides of the equation to eliminate the square root.
- Solve the resulting equation.
- Check your solution to ensure it is valid within the context of the original equation.
Example: Solve \(\sqrt{2x + 3} = 7\)
- Square both sides: \((\sqrt{2x + 3})^2 = 7^2\)
- Simplify: \(2x + 3 = 49\)
- Solve for \(x\): \(2x = 46\)
- Divide by 2: \(x = 23\)
Practice Makes Perfect
Consistent practice with these worksheets will enhance your ability to solve square root equations and deepen your understanding of algebraic principles.

READ MORE:
Introduction to Square Root Equations
Square root equations are a fundamental aspect of algebra, often encountered in both basic and advanced mathematics. These equations involve the square root of a variable and can be solved using various techniques. Understanding the principles behind square root equations is crucial for solving them accurately and efficiently.
Here's a step-by-step approach to solving square root equations:
- Isolate the Square Root:
Ensure that the square root expression is isolated on one side of the equation. For example, in the equation \( \sqrt{x} = 5 \), the square root is already isolated.
- Square Both Sides:
To eliminate the square root, square both sides of the equation. Using our example, \( \sqrt{x} = 5 \) becomes \( x = 25 \) after squaring both sides.
- Solve for the Variable:
After squaring, solve the resulting equation for the variable. If the equation was \( x + 3 = \sqrt{y} \), after isolating and squaring, it would become \( x^2 + 6x + 9 = y \).
- Check for Extraneous Solutions:
It is essential to check your solutions in the original equation because squaring both sides can introduce extraneous solutions that do not satisfy the initial equation.
By following these steps and practicing with a variety of problems, students can develop a strong understanding of how to solve square root equations efficiently.
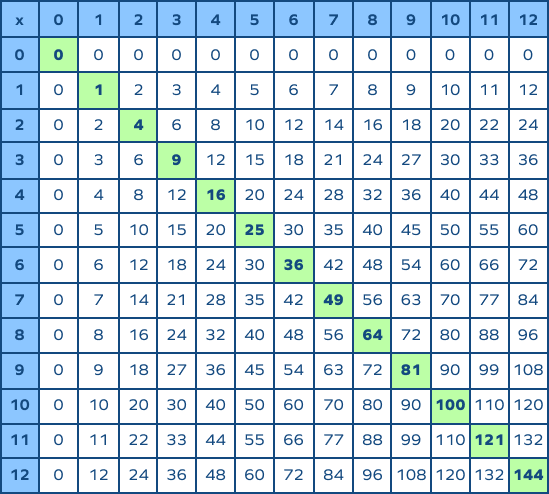
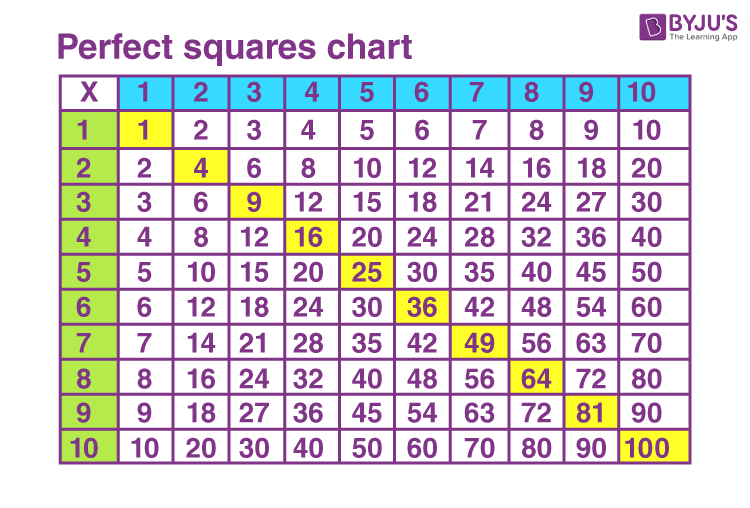
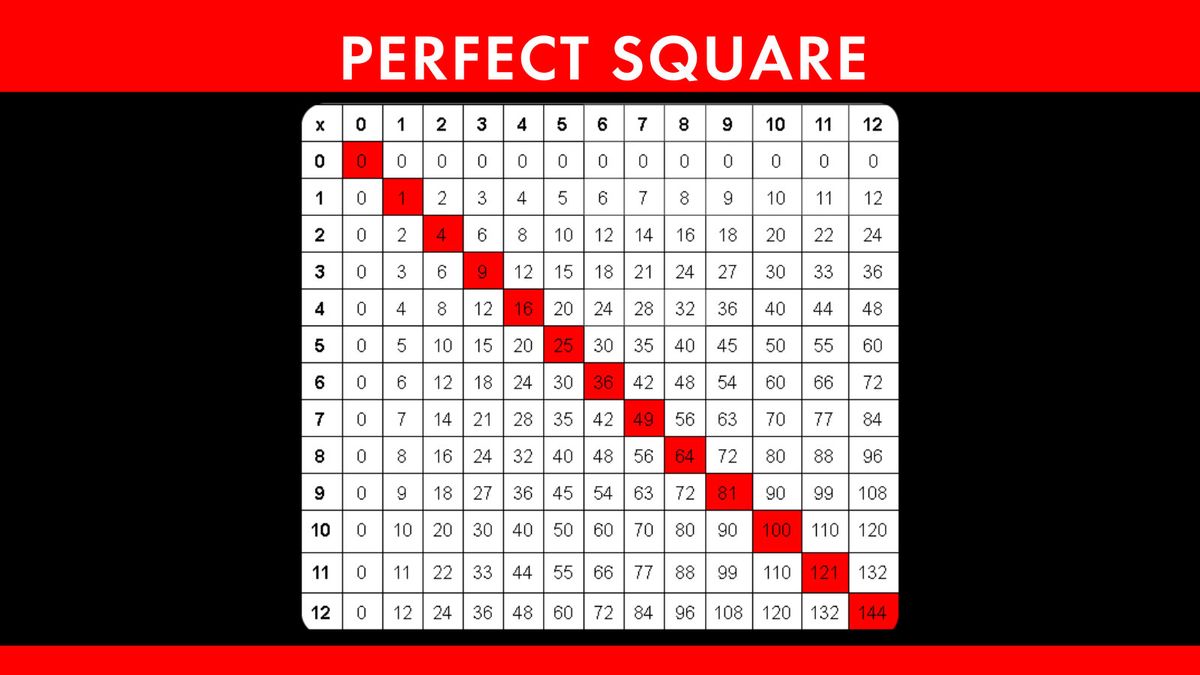
Understanding Square Roots
Square roots are a fundamental concept in mathematics that represent a value which, when multiplied by itself, gives the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \).
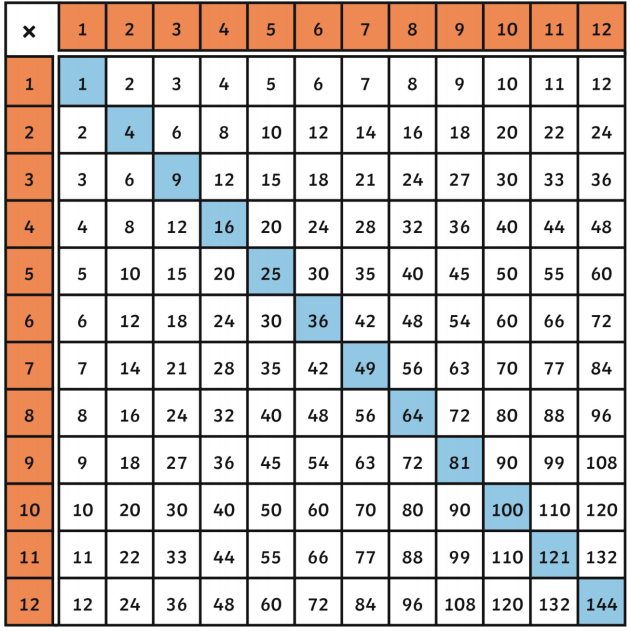
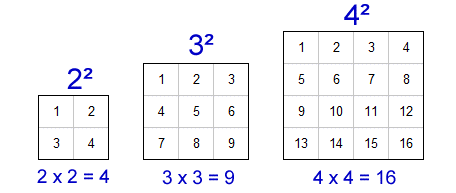
For example, \( \sqrt{9} = 3 \) because \( 3 \times 3 = 9 \). Similarly, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
When working with square roots, it's important to understand both perfect squares and non-perfect squares. Perfect squares are numbers like 1, 4, 9, 16, 25, etc., which have whole number square roots. Non-perfect squares are numbers like 2, 3, 5, 7, etc., which have square roots that are irrational numbers (cannot be expressed as a simple fraction).
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For instance, \( \sqrt{25} = 5 \) and \( \sqrt{25} = -5 \).
- Square Roots of Negative Numbers: The square root of a negative number involves imaginary numbers. For example, \( \sqrt{-1} = i \), where \( i \) is the imaginary unit.
To solve square root equations, follow these steps:
- Isolate the square root: If the equation is \( \sqrt{x} = y \), make sure the square root term is by itself on one side of the equation.
- Square both sides: Remove the square root by squaring both sides of the equation, giving \( x = y^2 \).
- Solve for the variable: Once the square root is removed, solve the resulting equation for the unknown variable.
- Check for extraneous solutions: Squaring both sides of an equation can introduce extraneous solutions. Substitute your solutions back into the original equation to verify their validity.
Understanding and practicing these steps is essential for mastering square roots and their applications in various mathematical problems.
Basic Square Root Equations
Square root equations often appear in algebra, and learning how to solve them is an essential skill. A square root equation includes a variable under a square root symbol. To solve these equations, follow these steps:
- Isolate the square root on one side of the equation.
- Square both sides of the equation to eliminate the square root.
- Solve the resulting equation.
- Check all solutions in the original equation to ensure they are valid, as squaring both sides can introduce extraneous solutions.
Let's explore some examples to understand this better:
-
Example 1: Solve \( \sqrt{x} = 5 \)
- Square both sides: \( (\sqrt{x})^2 = 5^2 \)
- This simplifies to: \( x = 25 \)
- Check: \( \sqrt{25} = 5 \) (Correct!)
-
Example 2: Solve \( \sqrt{2x + 3} = 7 \)
- Square both sides: \( (\sqrt{2x + 3})^2 = 7^2 \)
- This simplifies to: \( 2x + 3 = 49 \)
- Solve for \( x \): \( 2x = 46 \)
- \( x = 23 \)
- Check: \( \sqrt{2(23) + 3} = \sqrt{46 + 3} = \sqrt{49} = 7 \) (Correct!)
Practicing with a variety of square root equations will help build your confidence and improve your problem-solving skills. Worksheets can provide additional practice and reinforce these concepts.
Advanced Square Root Equations
In this section, we will delve into more complex square root equations that go beyond the basics. We will explore methods to solve equations that involve multiple square roots, square roots combined with other algebraic expressions, and higher-order roots.
Equations with Multiple Square Roots
To solve equations with multiple square roots, we often need to isolate one of the square roots and then square both sides of the equation to eliminate it. This process may need to be repeated until all square roots are removed. Here is a step-by-step example:
- Consider the equation: \(\sqrt{x + 3} + \sqrt{x - 2} = 5\)
- Isolate one of the square roots: \(\sqrt{x + 3} = 5 - \sqrt{x - 2}\)
- Square both sides: \(x + 3 = (5 - \sqrt{x - 2})^2\)
- Expand the right-hand side: \(x + 3 = 25 - 10\sqrt{x - 2} + x - 2\)
- Simplify: \(3 = 23 - 10\sqrt{x - 2}\)
- Isolate the remaining square root: \(10\sqrt{x - 2} = 20\)
- Solve for \(x\): \(\sqrt{x - 2} = 2 \implies x - 2 = 4 \implies x = 6\)
- Check the solution in the original equation to ensure it is valid.
Equations with Square Roots and Other Algebraic Terms
When solving equations that combine square roots with other algebraic terms, it is important to isolate the square root term before squaring both sides of the equation. Let's look at an example:
- Solve the equation: \(\sqrt{2x + 5} - x = 1\)
- Isolate the square root: \(\sqrt{2x + 5} = x + 1\)
- Square both sides: \(2x + 5 = (x + 1)^2\)
- Expand the right-hand side: \(2x + 5 = x^2 + 2x + 1\)
- Rearrange to form a quadratic equation: \(x^2 - 4 = 0\)
- Factorize: \((x - 2)(x + 2) = 0\)
- Solve for \(x\): \(x = 2\) or \(x = -2\)
- Check both solutions in the original equation to verify their validity.
Equations Involving Higher-Order Roots
Sometimes, equations may involve higher-order roots such as cube roots. The approach to solving these equations is similar but requires cubing both sides instead of squaring. Consider the following example:
- Solve the equation: \(\sqrt[3]{x + 7} = 2\)
- Cubing both sides: \(x + 7 = 2^3\)
- Simplify: \(x + 7 = 8\)
- Solve for \(x\): \(x = 1\)
- Verify the solution by substituting back into the original equation.
Practice Problems
Try solving the following advanced square root equations:
- \(\sqrt{3x + 4} + \sqrt{x - 1} = 7\)
- \(\sqrt{5x - 2} - \sqrt{2x + 1} = 3\)
- \(\sqrt[3]{2x + 1} + \sqrt[3]{x - 2} = 3\)
Remember to check all potential solutions in the original equations to ensure they are valid.

Solving Techniques for Square Root Equations
Solving square root equations involves a few key techniques to ensure accuracy and efficiency. Here are the steps and methods to solve these types of equations:
1. Isolate the Square Root
Begin by isolating the square root expression on one side of the equation. This makes it easier to eliminate the square root in the next step.
- Example: \(\sqrt{2x + 3} = 5\)
2. Square Both Sides
To eliminate the square root, square both sides of the equation. This will help you to transform the equation into a more manageable form.
- Example: \((\sqrt{2x + 3})^2 = 5^2\)
- Result: \(2x + 3 = 25\)
3. Solve the Resulting Equation
Once the square root is removed, solve the resulting linear or quadratic equation.
- Example: \(2x + 3 = 25\)
- Simplify: \(2x = 22\)
- Result: \(x = 11\)
4. Check for Extraneous Solutions
After finding the solutions, it's crucial to substitute them back into the original equation to verify their validity. Squaring both sides can sometimes introduce extraneous solutions that do not satisfy the original equation.
- Example: Check if \(x = 11\) satisfies the original equation \(\sqrt{2(11) + 3} = 5\)
- Calculation: \(\sqrt{22 + 3} = \sqrt{25} = 5\)
- Since it holds true, \(x = 11\) is a valid solution.
Example Problems
Here are some example problems and their step-by-step solutions:
-
Problem: \(\sqrt{3x - 7} + 2 = 0\)
- Isolate the square root: \(\sqrt{3x - 7} = -2\)
- Note: Since the square root of a number cannot be negative, this equation has no real solution.
-
Problem: \(\sqrt{x + 4} = x - 2\)
- Square both sides: \((\sqrt{x + 4})^2 = (x - 2)^2\)
- Result: \(x + 4 = x^2 - 4x + 4\)
- Rearrange into a quadratic equation: \(x^2 - 5x = 0\)
- Factorize: \(x(x - 5) = 0\)
- Solutions: \(x = 0\) or \(x = 5\)
- Check solutions in the original equation:
- For \(x = 0\): \(\sqrt{0 + 4} = 0 - 2\) (Invalid)
- For \(x = 5\): \(\sqrt{5 + 4} = 5 - 2\) (Valid)
- Valid solution: \(x = 5\)
Additional Tips
- Always perform a check by substituting the solutions back into the original equation.
- Be cautious of extraneous solutions that can arise from squaring both sides of the equation.
- Ensure all steps maintain the equation's balance by performing the same operations on both sides.
With these techniques and careful practice, solving square root equations becomes a more straightforward and systematic process.
Common Mistakes and Tips
When solving square root equations, students often make several common mistakes. Below are some of these mistakes along with tips to avoid them:
-
Failing to Isolate the Square Root:
Before squaring both sides of the equation, ensure that the square root term is isolated. For example, in the equation \( \sqrt{x} + 2 = 5 \), subtract 2 from both sides to isolate the square root term: \( \sqrt{x} = 3 \). Then square both sides to solve for \( x \).
-
Ignoring Extraneous Solutions:
Squaring both sides of an equation can introduce extraneous solutions. Always substitute your solutions back into the original equation to verify their validity. For example, solving \( \sqrt{x+1} = x - 1 \) might yield two solutions, but not all may satisfy the original equation.
-
Incorrectly Simplifying Radicals:
Make sure to simplify square roots correctly. For example, \( \sqrt{50} \) should be simplified to \( 5\sqrt{2} \), not \( 7.07 \).
-
Overlooking the Domain of the Equation:
Square root functions are only defined for non-negative values under the radical. Always check that the solutions fall within the domain of the original equation. For instance, \( \sqrt{x-3} = x - 5 \) implies \( x \geq 3 \).
Steps to Correctly Solve Square Root Equations
-
Isolate the Square Root: Move all terms without square roots to the other side of the equation.
Example: Solve \( \sqrt{2x + 3} - 1 = x \).
- Add 1 to both sides: \( \sqrt{2x + 3} = x + 1 \).
-
Square Both Sides: Eliminate the square root by squaring both sides of the equation.
Example: \( (\sqrt{2x + 3})^2 = (x + 1)^2 \).
- Simplify: \( 2x + 3 = x^2 + 2x + 1 \).
-
Solve the Resulting Equation: Use algebraic methods to solve the equation obtained after squaring.
Example: \( x^2 + 2x + 1 - 2x - 3 = 0 \) simplifies to \( x^2 - 2 = 0 \).
- Solve for \( x \): \( x^2 = 2 \) and \( x = \pm \sqrt{2} \).
-
Check for Extraneous Solutions: Substitute the solutions back into the original equation to ensure they are valid.
Example: Verify \( x = \sqrt{2} \) and \( x = -\sqrt{2} \) in the original equation \( \sqrt{2x + 3} - 1 = x \).
- Only \( x = \sqrt{2} \) is valid as it falls within the domain.
By following these steps and avoiding common mistakes, solving square root equations can become a straightforward process.
Square Root Equations in Word Problems
Square root equations often appear in various real-life word problems, requiring us to extract square roots as part of the solution process. Here are some techniques and examples to help you understand and solve these types of problems.
Steps to Solve Square Root Word Problems
- Read the Problem Carefully: Identify what is being asked and note down the important information.
- Translate the Problem into an Equation: Convert the word problem into a mathematical equation involving square roots.
- Solve the Equation: Use algebraic techniques to isolate the square root and then solve for the variable.
- Verify Your Solution: Check your solution by substituting it back into the original word problem.
Examples of Square Root Word Problems
Example 1: The floor of a square room is covered with square-foot tiles. If 81 tiles cover the floor, how long is each side of the room?
Solution: The area of the floor is 81 square feet. Since the floor is square, each side is the square root of 81.
\[
\sqrt{81} = 9 \text{ feet}
\]Example 2: A pool is twice as long as it is wide and is surrounded by a walkway of uniform width of 1 foot. The combined area of the pool and the walkway is 400 square feet. Find the dimensions of the pool.
Solution: Let the width of the pool be \( w \) feet. Then the length is \( 2w \) feet. Including the walkway, the dimensions are \( (w + 2) \) feet and \( (2w + 2) \) feet. The equation for the area is:
\[
(w + 2)(2w + 2) = 400
\]Simplifying and solving the quadratic equation:
\[
2w^2 + 6w + 4 = 400 \\
2w^2 + 6w - 396 = 0 \\
w^2 + 3w - 198 = 0
\]Using the quadratic formula \( w = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \), we find:
\[
w = \frac{-3 \pm \sqrt{9 + 792}}{2} \\
w = \frac{-3 \pm 27}{2}
\]Since width cannot be negative, \( w = 12 \). The dimensions of the pool are 12 feet by 24 feet.
Tips for Solving Square Root Word Problems
- Always double-check your units and make sure your final answer makes sense in the context of the problem.
- If the problem involves areas or volumes, ensure you account for all parts of the shape or object being described.
- Use estimation to quickly check if your answer is reasonable before solving it algebraically.
Applications of Square Root Equations
Square root equations are prevalent in various real-world applications across different fields such as geometry, physics, and engineering. Below, we will explore some common applications and how to approach solving these problems.
1. Geometry
In geometry, square root equations are often used to find the dimensions of shapes. For example, if you need to find the side length of a square given its area, you can use the equation:
\[
s = \sqrt{A}
\]
where \(s\) is the side length and \(A\) is the area.
Example: A square patio has an area of 200 square feet. To find the length of one side, solve the equation:
\[
s = \sqrt{200} \approx 14.1 \text{ feet}
\]
2. Physics
In physics, square root equations often appear in formulas involving time, distance, and acceleration. For instance, the equation for the period \(T\) of a simple pendulum is:
\[
T = 2\pi \sqrt{\frac{L}{g}}
\]
where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity.
3. Engineering
Engineering applications might include finding the stress on a material or the frequency of a vibrating system. For example, the natural frequency \(f\) of a beam can be found using:
\[
f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
\]
where \(k\) is the stiffness of the beam and \(m\) is the mass.
4. Economics
Square root equations can also be applied in economics to model various financial equations. For example, the standard deviation of a set of data, which measures the amount of variation or dispersion, is given by:
\[
\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}
\]
where \(\sigma\) is the standard deviation, \(N\) is the number of observations, \(x_i\) are the data points, and \(\mu\) is the mean of the data points.
Problem Solving Steps
- Read the problem carefully and understand all the given information.
- Identify what you need to find.
- Assign variables to the unknown quantities.
- Set up the equation based on the given information and formulas.
- Solve the equation using appropriate algebraic techniques.
- Verify the solution by substituting it back into the original context of the problem.
- Interpret the solution and ensure it makes sense in the context of the problem.
By following these steps and understanding the applications of square root equations, you can solve a wide range of practical problems effectively.

Practice Worksheets
Practice worksheets are an essential part of mastering square root equations. These worksheets provide a variety of problems that help students apply their understanding and improve their skills. Below are some practice worksheets designed to cater to different levels of proficiency.
Basic Square Root Problems
- Calculate the square roots of perfect squares:
- \(\sqrt{25} = 5\)
- \(\sqrt{36} = 6\)
- \(\sqrt{49} = 7\)
Intermediate Problems
- Simplify square roots of non-perfect squares:
- \(\sqrt{20} = 2\sqrt{5}\)
- \(\sqrt{45} = 3\sqrt{5}\)
- \(\sqrt{72} = 6\sqrt{2}\)
- Solve square root equations:
- \(\sqrt{x + 4} = 3\)
Solution: \(x + 4 = 9 \Rightarrow x = 5\)
- \(\sqrt{2x - 1} = 4\)
Solution: \(2x - 1 = 16 \Rightarrow x = 8.5\)
- \(\sqrt{x + 4} = 3\)
Advanced Problems
- Solve complex square root equations:
- \(\sqrt{x + 2} + \sqrt{x - 3} = 5\)
Solution:
- Let \( \sqrt{x + 2} = a \) and \( \sqrt{x - 3} = b \)
- Then, \( a + b = 5 \) and \( a^2 = x + 2 \), \( b^2 = x - 3 \)
- So, \( x = a^2 - 2 \) and \( x = b^2 + 3 \)
- Equate and solve: \( a^2 - 2 = b^2 + 3 \)
- Solve system of equations: \(a + b = 5\) and \(a^2 - b^2 = 5\)
- \(\sqrt{3x + 1} = 2\sqrt{x - 2}\)
Solution:
- Square both sides: \(3x + 1 = 4(x - 2)\)
- Simplify and solve: \(3x + 1 = 4x - 8 \Rightarrow x = 9\)
- \(\sqrt{x + 2} + \sqrt{x - 3} = 5\)
Downloadable Worksheets
For additional practice, you can download and print these worksheets:
Answer Keys
Below are the answer keys for the practice worksheets. Use these to check your solutions and ensure your understanding of solving square root equations.
| Worksheet | Question | Answer |
|---|---|---|
| 1 | \(\sqrt{144}\) | 12 |
| 1 | \(\sqrt{81}\) | 9 |
| 1 | \(\sqrt{225}\) | 15 |
| 2 | \(\sqrt{196}\) | 14 |
| 2 | \(\sqrt{64}\) | 8 |
| 2 | \(\sqrt{49}\) | 7 |
| 3 | \(\sqrt{169}\) | 13 |
| 3 | \(\sqrt{36}\) | 6 |
| 3 | \(\sqrt{100}\) | 10 |
Below are step-by-step solutions for some of the more complex problems:
-
Worksheet 1, Question 5: Solve \( \sqrt{784} \)
Step 1: Identify the number inside the square root: 784
Step 2: Find the square root of 784
Solution: \( \sqrt{784} = 28 \)
-
Worksheet 2, Question 3: Solve \( \sqrt{121} \)
Step 1: Identify the number inside the square root: 121
Step 2: Find the square root of 121
Solution: \( \sqrt{121} = 11 \)
-
Worksheet 3, Question 7: Solve \( \sqrt{625} \)
Step 1: Identify the number inside the square root: 625
Step 2: Find the square root of 625
Solution: \( \sqrt{625} = 25 \)
Check all your answers against the solutions provided to ensure you understand the methods used to solve square root equations correctly.
Bài Tập Chìa Khóa: Giải Phương Trình Căn Bậc Hai
READ MORE:
Khám phá cách giải các phương trình căn bậc hai với bài tập minh họa chi tiết trong video này.
Bài Tập Chính - Giải Phương Trình Căn Bậc Hai