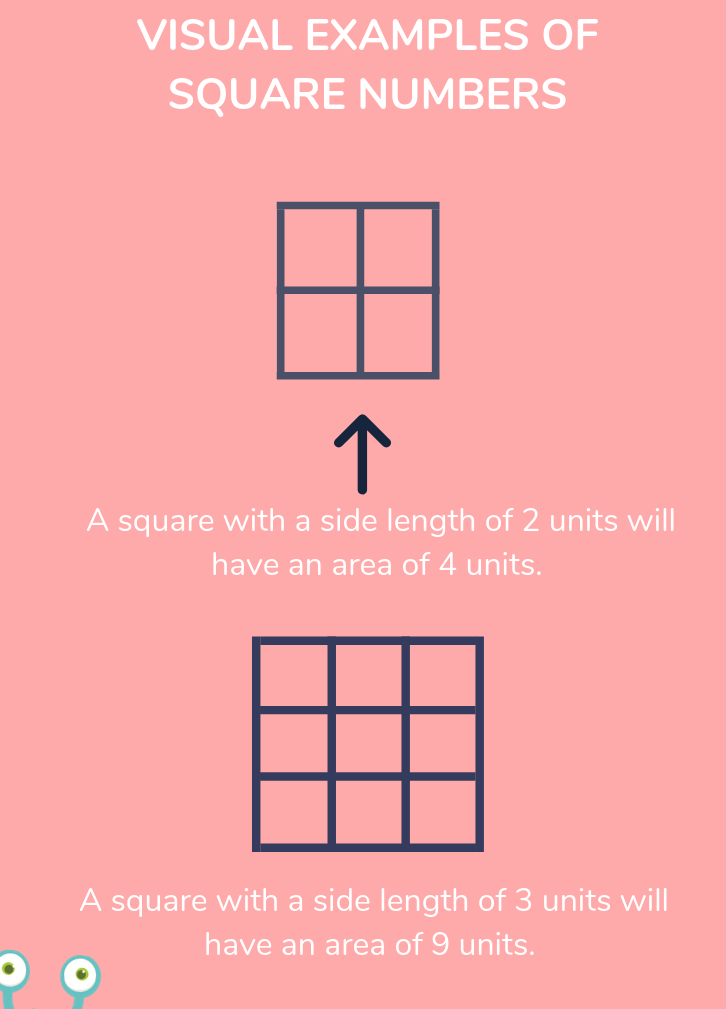Topic squares and square roots worksheet pdf: Discover comprehensive worksheets on squares and square roots, perfect for enhancing math skills in grades 6 through 8. These PDFs provide a variety of problems designed to help students understand and practice the concepts of squaring numbers and finding square roots. Ideal for classroom use, homework assignments, or self-study, these worksheets are a valuable resource for both teachers and students.
Table of Content
- Squares and Square Roots Worksheet PDF
- Table of Contents
- Introduction to Squares and Square Roots
- Basic Concepts and Definitions
- Finding the Square of a Number
- Finding the Square Root of a Number
- Properties of Squares and Square Roots
- Methods for Finding Square Roots
- Factorization Method
- Long Division Method
- Estimation Method
- Simplifying Square Roots
- Simplifying Square Roots with Negative Numbers
- Common Mistakes and How to Avoid Them
- Practice Worksheets
- Worksheet 1: Basic Problems
- Worksheet 2: Intermediate Problems
- Worksheet 3: Advanced Problems
- Worksheet 4: Real-life Applications
- YOUTUBE: Video hướng dẫn về lũy thừa và căn bậc hai từ Math Antics, giúp học sinh nắm vững các khái niệm toán học cơ bản.
Squares and Square Roots Worksheet PDF
Enhance your mathematical skills with our comprehensive collection of squares and square roots worksheets. These resources are designed to help students master the concepts of squaring numbers and finding their square roots. Suitable for various grade levels, these worksheets are perfect for classroom use, homeschooling, or individual practice.
Available Worksheets
-
Basic Squares and Square Roots
- Squares and Square Roots (A) -
- Squares and Square Roots Worksheet - 1 -
- Square Root Worksheets -
-
Advanced Practice
- Simplifying Square Roots with Negative Numbers -
- Finding Square Roots of Non-Perfect Squares -
Key Concepts Covered
- Understanding and calculating squares of numbers
- Finding square roots of perfect and non-perfect squares
- Simplifying square roots, including those with negative numbers
- Practical applications of squares and square roots in problem-solving
Example Problems
Below are some example problems you can find in these worksheets:
- Find the square of 12.
- Calculate the square root of 144.
- Simplify the square root of 50.
- Determine the perimeter of a square with an area of 64 cm2.
How to Use
These worksheets can be used in a variety of educational settings:
- Teachers: Assign these worksheets as practice assignments, quizzes, or group activities.
- Parents: Use these resources to give your children extra practice or to reinforce learning during school breaks.
- Students: Utilize these worksheets for self-study, review, or peer tutoring.
Download and Print
Click on the links provided to download and print the worksheets in PDF format. Each worksheet includes answers on the second page for easy self-assessment.
Start enhancing your mathematical skills today with our detailed squares and square roots worksheets!

READ MORE:
Table of Contents
- Introduction to Squares and Square Roots
- Understanding Perfect Squares
- Finding the Square of a Number
- Methods to Calculate Square Roots
- Using Factorization to Find Square Roots
- Long Division Method for Square Roots
- Simplifying Square Roots
- Square Roots of Negative Numbers
- Applications of Squares and Square Roots
- Practice Worksheets and Exercises
- Answer Keys and Solutions
Introduction to Squares and Square Roots
Understanding squares and square roots is fundamental in mathematics, especially in areas involving algebra and geometry. A square of a number is the result of multiplying the number by itself, while a square root is a value that, when multiplied by itself, gives the original number. Mastering these concepts can enhance problem-solving skills and is essential for higher-level math.
- Definition of Squares
- Definition of Square Roots
- Properties of Squares and Square Roots
- How to Calculate Squares
- How to Calculate Square Roots
- Applications in Real-life Problems
- Practice Problems and Worksheets
- Advanced Concepts in Squares and Square Roots
| Concept | Example |
|---|---|
| Square of a Number | \(5^2 = 25\) |
| Square Root of a Number | \(\sqrt{25} = 5\) |
By regularly practicing with worksheets on squares and square roots, students can solidify their understanding and improve their mathematical proficiency. Printable worksheets and PDF resources are available to provide comprehensive practice opportunities.
Basic Concepts and Definitions
Understanding squares and square roots is fundamental to mastering various mathematical concepts. Below are some basic definitions and examples to get you started.
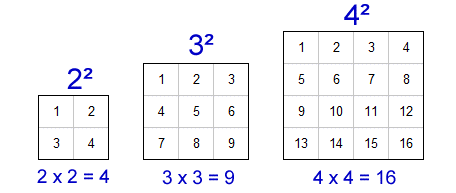
- Square of a Number: The square of a number is the result of multiplying the number by itself. For example, the square of 5 is \(5^2 = 5 \times 5 = 25\).
- Square Root of a Number: The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is \(\sqrt{25} = 5\).
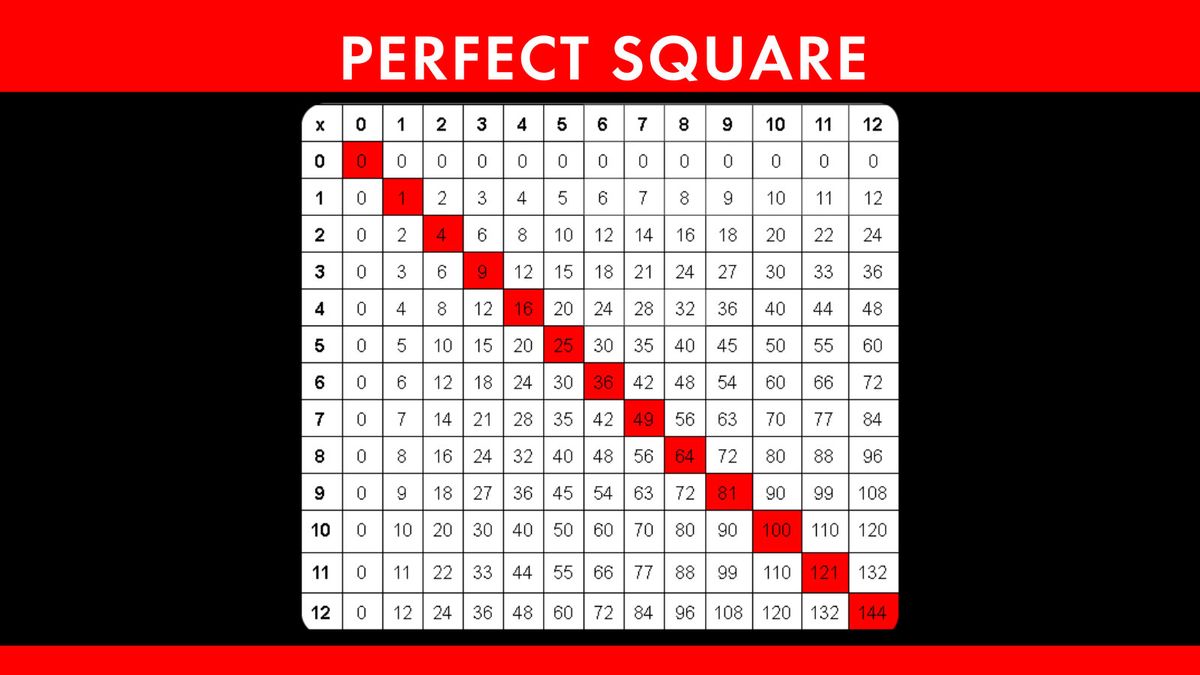
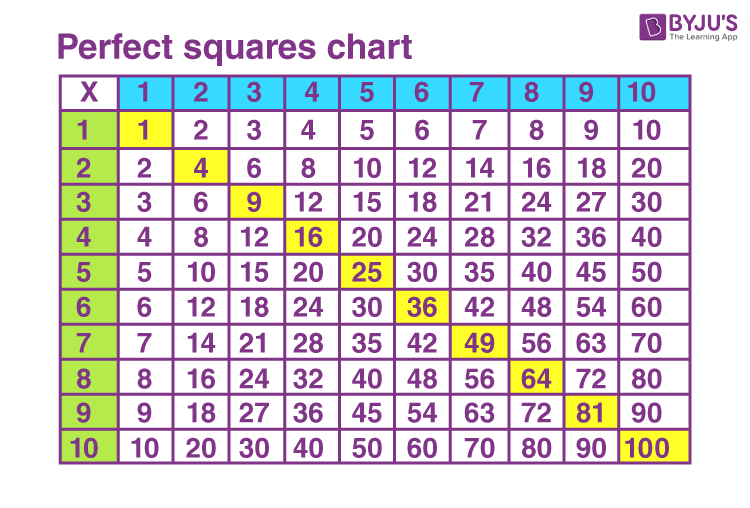
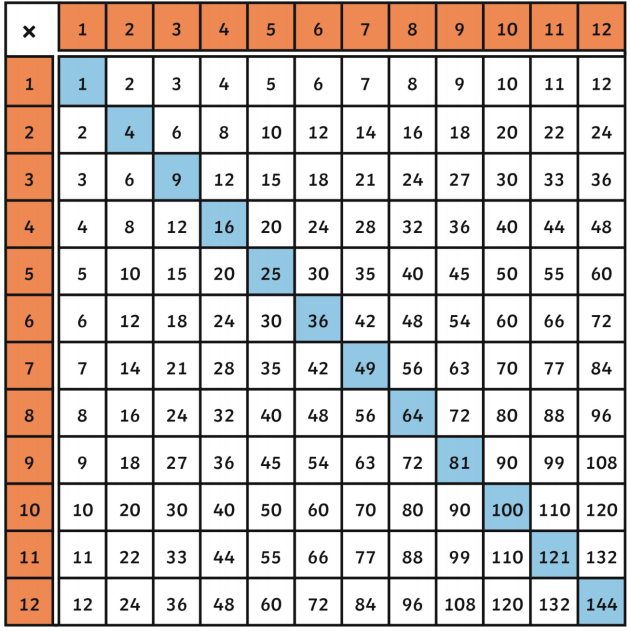
- Perfect Squares: Numbers that are squares of integers are called perfect squares. Examples include 1, 4, 9, 16, 25, etc.
- Notation: The square of a number \(n\) is written as \(n^2\) and the square root of a number \(n\) is written as \(\sqrt{n}\).
Examples
- Example 1: \(4^2 = 4 \times 4 = 16\)
- Example 2: \(\sqrt{16} = 4\)
- Example 3: \(9^2 = 9 \times 9 = 81\)
- Example 4: \(\sqrt{81} = 9\)
Properties of Squares and Square Roots
- Non-negative Results: The square of any real number is always non-negative.
- Inverse Relationship: Squaring and taking the square root are inverse operations.
- Even and Odd Properties: The square of an even number is even, and the square of an odd number is odd.
Applications
Understanding squares and square roots is crucial for solving quadratic equations, working with exponents, and in various geometry problems. Mastering these concepts can greatly enhance problem-solving skills in mathematics.
Finding the Square of a Number
Finding the square of a number is a fundamental mathematical operation that involves multiplying a number by itself. This section will guide you through the step-by-step process of calculating squares and provide practical examples for better understanding.
-
Definition: The square of a number \( n \) is denoted as \( n^2 \) and is calculated by \( n \times n \). For example, the square of 4 is \( 4^2 = 4 \times 4 = 16 \).
-
Steps to Find the Square:
- Identify the number you want to square.
- Multiply the number by itself.
- Write down the result, which is the square of the number.
-
Examples:
Number Square 3 9 5 25 7 49 -
Applications: Squaring numbers is used in various mathematical calculations, including geometry (calculating area), algebra (solving quadratic equations), and statistics (variance and standard deviation).

Finding the Square Root of a Number
Finding the square root of a number involves determining a value that, when multiplied by itself, gives the original number. Here's a step-by-step guide:
- Estimate: Begin by estimating the square root. You can do this by finding the closest perfect squares above and below the given number. For example, if you want to find the square root of 20, the closest perfect squares are 16 (4^2) and 25 (5^2). Since 20 is closer to 16, you might estimate the square root to be between 4 and 5.
- Guess and Check: Make an initial guess based on your estimation. For instance, if you estimated the square root of 20 to be between 4 and 5, you might start with 4.5.
- Test Your Guess: Square your guess and compare it with the original number. If it's too high, try a smaller number; if it's too low, try a larger number. For example, squaring 4.5 gives 20.25, which is too high. So, you might try a smaller number.
- Refine Your Guess: Based on the result of your test, adjust your guess accordingly. In this case, you might try a number between 4 and 4.5, such as 4.2.
- Repeat: Continue this process of guessing and refining until you find a value that's very close to the square root of the original number.
Alternatively, you can use various methods to find the square root more precisely, such as the Babylonian method or using a calculator or computer program.
Properties of Squares and Square Roots
Understanding the properties of squares and square roots can help simplify calculations and solve mathematical problems more efficiently. Here are some important properties to know:
- Identity Property: The square of any number is always non-negative. In other words, for any real number x, \( x^2 \geq 0 \).
- Zero Property: The square of 0 is 0, which means \( 0^2 = 0 \).
- One Property: The square of 1 is 1, so \( 1^2 = 1 \).
- Negative Property: The square of a negative number is positive. For example, \( (-x)^2 = x^2 \).
- Product Property: The square of a product is the product of the squares. This property can be expressed as \( (xy)^2 = x^2 y^2 \).
- Quotient Property: The square of a quotient is the quotient of the squares. In other words, \( \left(\frac{x}{y}\right)^2 = \frac{x^2}{y^2} \), provided y ≠ 0.
- Reciprocal Property: The square of a reciprocal is the reciprocal of the square. This property states that \( \left(\frac{1}{x}\right)^2 = \frac{1}{x^2} \), provided x ≠ 0.
- Root Property: The square root of a product is the product of the square roots. Mathematically, \( \sqrt{xy} = \sqrt{x} \sqrt{y} \).
- Exponent Property: The square root of a number raised to a power is the number raised to half of that power. This can be represented as \( \sqrt{x^a} = x^{\frac{a}{2}} \).
These properties can be applied in various mathematical contexts to simplify expressions, solve equations, and understand the behavior of squares and square roots.
Methods for Finding Square Roots
Finding square roots can be approached using various methods, each suited to different situations and preferences. Here are some common methods:
- Prime Factorization Method: This method involves breaking down the number into its prime factors and then pairing them up. For each pair, take one factor from each pair and multiply them together to find the square root.
- Estimation Method: Estimating the square root involves finding the nearest perfect square above and below the given number. Then, guess a value between the square roots of these perfect squares and refine the guess iteratively until reaching an accurate result.
- Repeated Subtraction Method: This method is a simple iterative process where you repeatedly subtract odd numbers starting from 1 until reaching 0. The number of times you subtract corresponds to the square root of the original number.
- Newton's Method (or Newton-Raphson Method): Newton's method is an iterative algorithm that uses calculus to approximate the square root of a number. It involves repeatedly applying a formula that converges to the square root.
- Babylonian Method: Also known as Heron's method, this ancient algorithm is a fast and efficient way to approximate square roots. It involves making an initial guess and then refining it using a specific formula until reaching a satisfactory approximation.
- Using Tables: Some square roots can be found using pre-calculated tables of square roots. This method is less common today but was historically important for manual calculations.
- Calculator or Computer: Perhaps the most convenient method in modern times, using a calculator or computer program to find square roots is fast and accurate. Most scientific calculators and software have built-in functions for calculating square roots.
Each method has its advantages and disadvantages, and the choice of method often depends on the context of the problem and the available resources.
Factorization Method
The factorization method for finding square roots involves breaking down the given number into its prime factors and then pairing them up. Here's how to use this method:
- Prime Factorization: Begin by finding the prime factorization of the given number. This involves breaking down the number into its prime factors, which are the prime numbers that multiply together to give the original number.
- Pairing Factors: Once you have the prime factors, pair them up. Each pair of prime factors represents a square root.
- Extracting Square Roots: For each pair of prime factors, take one factor from each pair and multiply them together. This product gives one possible square root of the original number.
- Final Result: If there are any leftover prime factors that couldn't be paired, multiply them together to find the remaining part of the square root. This may result in an irrational number if the original number is not a perfect square.
Let's illustrate this method with an example:
| Example: | Find the square root of 72 using the factorization method. |
| Solution: |
|
The factorization method is particularly useful for finding square roots of non-perfect square numbers and expressing them in simplified radical form.

Long Division Method
The long division method for finding square roots is a systematic approach that involves dividing the given number into smaller parts and iteratively finding the square root of each part. Here's how to use this method:
- Group Digits: Begin by grouping the digits of the given number into pairs, starting from the decimal point (if applicable) and working towards the left. If there's an odd number of digits, the leftmost group will have only one digit.
- Divide and Conquer: Start with the leftmost group of digits. Find the largest integer whose square is less than or equal to the leftmost group. This integer becomes the first digit of the square root.
- Divide and Subtract: Multiply this digit by itself and subtract the result from the leftmost group. Bring down the next pair of digits (if any) to the right of the remainder.
- Repeat: Repeat steps 2 and 3 with the new dividend (the result of the subtraction) and the next pair of digits brought down. Continue this process until all pairs of digits have been processed.
- Decimal Point: If there are decimals in the original number, place the decimal point in the quotient above the decimal point in the original number and continue the division process as needed.
- Final Result: Once all pairs of digits have been processed, the quotient obtained represents the square root of the original number.
Let's illustrate this method with an example:
| Example: | Find the square root of 784 using the long division method. |
| Solution: |
|
The long division method provides a step-by-step process for finding square roots, particularly useful for larger numbers or when an approximation is needed.
Estimation Method
The estimation method for finding square roots involves approximating the square root of a number by identifying the closest perfect squares above and below the given number. Here's how to use this method:
- Identify Perfect Squares: Start by identifying the perfect squares that are closest to the given number. These perfect squares act as reference points for estimation.
- Choose a Starting Point: Determine a starting point for your estimation. This can be the square root of the lower perfect square or the square root of the higher perfect square, depending on which is closer to the given number.
- Guess and Adjust: Make an initial guess for the square root based on your starting point. If the guess is too high, try a smaller value; if it's too low, try a larger value. Adjust your guess iteratively until you find a value that's close to the actual square root.
- Verify: Once you have a tentative square root, verify its accuracy by squaring it and comparing the result with the original number. If necessary, refine your estimation further.
Let's illustrate this method with an example:
| Example: | Estimate the square root of 30 using the estimation method. |
| Solution: |
|
The estimation method provides a quick and intuitive way to approximate square roots, useful for mental math and rough calculations.
Simplifying Square Roots
Simplifying square roots involves expressing them in their simplest form by removing any perfect square factors from the radicand. Here's how to simplify square roots:
- Factorize the Radicand: Begin by factorizing the radicand (the expression under the square root sign) into its prime factors.
- Identify Perfect Square Factors: Identify any perfect square factors among the prime factors. These are factors that appear in pairs.
- Extract Perfect Squares: For each pair of perfect square factors, take one factor out of the square root sign. This reduces the power of the factor by half.
- Multiply Outside the Square Root: Multiply together any factors left outside the square root sign.
- Final Result: Combine the factors inside and outside the square root sign to obtain the simplified form of the square root.
Let's illustrate this method with an example:
| Example: | Simplify \( \sqrt{72} \). |
| Solution: |
|
Simplifying square roots is useful for performing calculations, solving equations, and expressing solutions in a more concise form.
Simplifying Square Roots with Negative Numbers
Simplifying square roots involving negative numbers requires understanding the concept of imaginary numbers. Here's how to simplify square roots with negative numbers:
- Understand Imaginary Numbers: Recognize that the square root of a negative number is not a real number. Instead, it is an imaginary number denoted by \( i \).
- Factorize the Radicand: Begin by factorizing the absolute value of the negative number into its prime factors.
- Identify Perfect Square Factors: Identify any perfect square factors among the prime factors, as done in simplifying square roots of positive numbers.
- Extract Perfect Squares: For each pair of perfect square factors, take one factor out of the square root sign, just like in the case of positive numbers.
- Introduce Imaginary Unit: For any remaining factors inside the square root sign, introduce the imaginary unit \( i \).
- Final Result: Combine the real part (if any) and the imaginary part to obtain the simplified form of the square root with a negative radicand.
Let's illustrate this method with an example:
| Example: | Simplify \( \sqrt{-48} \). |
| Solution: |
|
Simplifying square roots with negative numbers involves manipulating imaginary units alongside real numbers, allowing for concise expression of complex numbers.

Common Mistakes and How to Avoid Them
While working with squares and square roots, it's common to encounter certain mistakes. Being aware of these mistakes can help you avoid them and improve your understanding of the concepts. Here are some common mistakes and how to avoid them:
- Forgetting Negative Sign: Forgetting to include the negative sign when simplifying square roots of negative numbers. Always remember to introduce the imaginary unit \( i \) when dealing with negative square roots.
- Ignoring Perfect Squares: Failing to recognize perfect square factors within the radicand when simplifying square roots. Always factorize the radicand and look for perfect square factors to simplify.
- Incorrect Application of Properties: Misapplying properties of squares and square roots, leading to incorrect simplification or calculation. Review and understand the properties carefully before applying them.
- Confusing Estimation with Exact Calculation: Confusing estimation methods with exact calculation methods when finding square roots. Understand the difference between estimation and precise calculation and choose the appropriate method accordingly.
- Skipping Verification: Failing to verify the accuracy of calculated square roots by squaring them and comparing the result with the original number. Always double-check your calculations to ensure accuracy.
- Overlooking Negative Solutions: Overlooking negative solutions when solving equations involving square roots. Remember that equations involving square roots may have both positive and negative solutions.
By being mindful of these common mistakes and practicing careful attention to detail, you can enhance your proficiency in working with squares and square roots, leading to more accurate results and deeper comprehension of mathematical concepts.
Practice Worksheets
Practice worksheets are invaluable tools for reinforcing your understanding of squares and square roots through hands-on exercises. Here's how to make the most of practice worksheets:
- Varied Exercises: Look for worksheets that offer a variety of exercises covering different aspects of squares and square roots, such as simplification, calculation, and application problems.
- Progressive Difficulty: Start with worksheets that offer problems of moderate difficulty level, gradually increasing the complexity as you become more confident in your skills.
- Systematic Approach: Work through the worksheets systematically, tackling one type of problem at a time to ensure thorough understanding and mastery.
- Review and Feedback: After completing each worksheet, review your answers and seek feedback if possible. Identify any mistakes and areas where you can improve.
- Regular Practice: Incorporate practice worksheets into your regular study routine to reinforce concepts and improve problem-solving skills consistently.
Additionally, consider creating your own practice worksheets based on specific areas you find challenging or want to focus on. This allows you to tailor the exercises to your individual learning needs and preferences.
Worksheet 1: Basic Problems
Welcome to the first worksheet on squares and square roots. This worksheet will help you practice and understand the basic concepts of finding squares and square roots of numbers. Let's get started with some fundamental problems.
Instructions:
- Find the square of each given number.
- Calculate the square root of each perfect square provided.
- Simplify each expression where necessary.
Part 1: Finding the Square of a Number
For each number below, find the square (i.e., the number multiplied by itself).
- 5
- 8
- 12
- 15
- 20
Solutions:
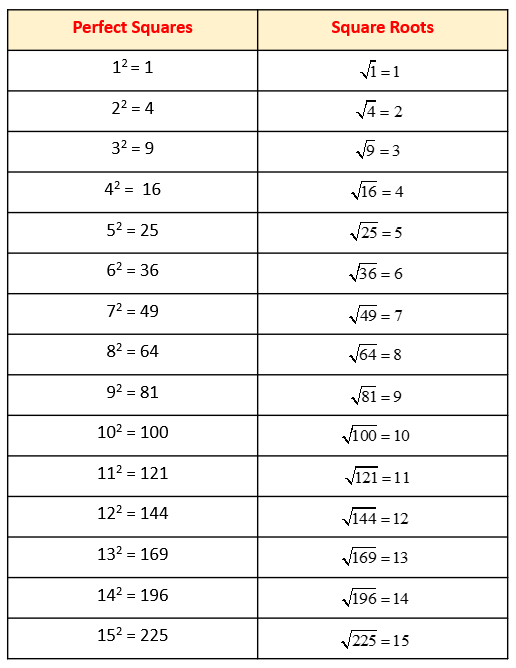
- \( 5^2 = 25 \)
- \( 8^2 = 64 \)
- \( 12^2 = 144 \)
- \( 15^2 = 225 \)
- \( 20^2 = 400 \)
Part 2: Finding the Square Root of a Number
Find the square root of each perfect square provided below.
- 36
- 49
- 81
- 100
- 144
Solutions:
- \( \sqrt{36} = 6 \)
- \( \sqrt{49} = 7 \)
- \( \sqrt{81} = 9 \)
- \( \sqrt{100} = 10 \)
- \( \sqrt{144} = 12 \)
Part 3: Simplifying Square Roots
Simplify each square root expression to its simplest form.
- \( \sqrt{50} \)
- \( \sqrt{72} \)
- \( \sqrt{98} \)
- \( \sqrt{128} \)
- \( \sqrt{200} \)
Solutions:
- \( \sqrt{50} = 5\sqrt{2} \)
- \( \sqrt{72} = 6\sqrt{2} \)
- \( \sqrt{98} = 7\sqrt{2} \)
- \( \sqrt{128} = 8\sqrt{2} \)
- \( \sqrt{200} = 10\sqrt{2} \)
Part 4: Word Problems
Solve the following word problems using your knowledge of squares and square roots.
- A square garden has an area of 64 square meters. What is the length of one side of the garden?
- If a square painting has a side length of 10 meters, what is its area?
- The area of a square is 121 square meters. Find the perimeter of the square.
Solutions:
- The length of one side is \( \sqrt{64} = 8 \) meters.
- The area of the painting is \( 10^2 = 100 \) square meters.
- The side length is \( \sqrt{121} = 11 \) meters, so the perimeter is \( 4 \times 11 = 44 \) meters.
Great job completing the worksheet! Continue practicing to master squares and square roots.
Worksheet 2: Intermediate Problems
Welcome to the intermediate level worksheet on squares and square roots. In this section, we will explore problems that involve more complex calculations and a deeper understanding of the concepts. Please attempt each problem and check your answers using the solutions provided at the end.
Instructions: Solve the following problems. Use a separate sheet of paper if necessary. Show all your work for full credit.
-
Find the square roots:
- \(\sqrt{169}\)
- \(\sqrt{256}\)
- \(\sqrt{484}\)
- \(\sqrt{529}\)
-
Evaluate the following expressions:
- \(3\sqrt{25} + 2\sqrt{49}\)
- \(\sqrt{144} - \sqrt{36}\)
- \(5\sqrt{16} \times \sqrt{9}\)
- \(\frac{\sqrt{225}}{\sqrt{25}}\)
-
Simplify the following radicals:
- \(\sqrt{75}\)
- \(\sqrt{200}\)
- \(\sqrt{320}\)
- \(\sqrt{450}\)
-
Solve the equations for \(x\):
- \(x^2 = 121\)
- \(x^2 - 64 = 0\)
- \(2x^2 = 98\)
- \(3x^2 + 75 = 0\)
-
Word Problems:
- A square garden has an area of 441 square meters. What is the length of one side of the garden?
- If the area of a square is increased by 300%, its new area becomes 400 square meters. What was the original area of the square?
- A number is decreased by 4 and then squared, resulting in 64. What is the number?
Solutions:
-
Find the square roots:
- \(\sqrt{169} = 13\)
- \(\sqrt{256} = 16\)
- \(\sqrt{484} = 22\)
- \(\sqrt{529} = 23\)
-
Evaluate the following expressions:
- \(3\sqrt{25} + 2\sqrt{49} = 3 \times 5 + 2 \times 7 = 15 + 14 = 29\)
- \(\sqrt{144} - \sqrt{36} = 12 - 6 = 6\)
- \(5\sqrt{16} \times \sqrt{9} = 5 \times 4 \times 3 = 60\)
- \(\frac{\sqrt{225}}{\sqrt{25}} = \frac{15}{5} = 3\)
-
Simplify the following radicals:
- \(\sqrt{75} = \sqrt{25 \times 3} = 5\sqrt{3}\)
- \(\sqrt{200} = \sqrt{100 \times 2} = 10\sqrt{2}\)
- \(\sqrt{320} = \sqrt{64 \times 5} = 8\sqrt{5}\)
- \(\sqrt{450} = \sqrt{225 \times 2} = 15\sqrt{2}\)
-
Solve the equations for \(x\):
- \(x^2 = 121 \Rightarrow x = \pm 11\)
- \(x^2 - 64 = 0 \Rightarrow x^2 = 64 \Rightarrow x = \pm 8\)
- \(2x^2 = 98 \Rightarrow x^2 = 49 \Rightarrow x = \pm 7\)
- \(3x^2 + 75 = 0 \Rightarrow x^2 = -25 \Rightarrow x = \pm 5i\) (Imaginary numbers)
-
Word Problems:
- Length of one side of the garden = \(\sqrt{441} = 21\) meters
- Original area of the square = \(\frac{400}{4} = 100\) square meters
- Let the number be \(x\). \((x-4)^2 = 64 \Rightarrow x - 4 = \pm 8 \Rightarrow x = 12 \text{ or } -4\)
Worksheet 3: Advanced Problems
In this section, you will tackle more challenging problems involving squares and square roots. These exercises will require you to apply advanced techniques and understanding of the concepts.
Instructions: Solve each problem below. Show all your work for full credit.
Part A: Perfect Squares and Square Roots
-
Find the square root of 324.
\(\sqrt{324} = \)
-
Calculate the square of 23.
\(23^2 = \)
-
Find the square root of 961.
\(\sqrt{961} = \)
-
Calculate the square of 37.
\(37^2 = \)
Part B: Non-Perfect Squares
-
Find the approximate square root of 50 (round to two decimal places).
\(\sqrt{50} \approx \)
-
Find the approximate square root of 200 (round to two decimal places).
\(\sqrt{200} \approx \)
-
Find the approximate square root of 123 (round to two decimal places).
\(\sqrt{123} \approx \)
Part C: Word Problems
-
A square garden has an area of 625 square meters. What is the length of one side of the garden?
Side length = \(\sqrt{625} = \)
-
The area of a square playground is 441 square meters. Calculate the perimeter of the playground.
Side length = \(\sqrt{441} = \)
Perimeter = 4 × side length =
-
If the area of a square is 784 square meters, what is the length of its diagonal? (Use the formula for the diagonal of a square: \(d = s\sqrt{2}\))
Side length = \(\sqrt{784} = \)
Diagonal = side length × \(\sqrt{2} = \)
Part D: Complex Numbers
-
Find the square root of -49.
\(\sqrt{-49} = \)
-
Calculate the square of the imaginary unit \(i\).
\(i^2 = \)
-
Find the square root of -121.
\(\sqrt{-121} = \)
Worksheet 4: Real-life Applications
Understanding squares and square roots can help solve practical problems in various real-life scenarios. This worksheet focuses on applying these mathematical concepts to real-world situations.
Problem 1: Architecture
Architects often use square roots to determine structural dimensions. Suppose you need to find the diagonal support length for a rectangular frame with sides of 8 feet and 6 feet.
- Calculate the diagonal using the Pythagorean theorem: \( \sqrt{8^2 + 6^2} \)
- Simplify the expression: \( \sqrt{64 + 36} = \sqrt{100} = 10 \)
So, the diagonal support length is 10 feet.
Problem 2: Finance
In finance, square roots are used to assess investment risks. If the variance of stock returns is 25, find the standard deviation to understand the risk.
- Standard deviation is the square root of the variance: \( \sqrt{25} \)
- Simplify the expression: \( \sqrt{25} = 5 \)
Thus, the standard deviation is 5.
Problem 3: Navigation
Square roots help in calculating distances between points. Find the distance between points (3, 4) and (7, 1) on a map.
- Use the distance formula: \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
- Substitute the coordinates: \( \sqrt{(7 - 3)^2 + (1 - 4)^2} \)
- Simplify the expression: \( \sqrt{4^2 + (-3)^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \)
The distance between the points is 5 units.
Problem 4: Cooking
Scaling recipes often requires squaring and square rooting. If a recipe calls for 9 teaspoons of a spice for a batch that serves 4, how much spice is needed for a batch that serves 16?
- Determine the scaling factor: \( \frac{16}{4} = 4 \)
- Use the square root of the scaling factor: \( \sqrt{4} = 2 \)
- Multiply the original amount by the scaling factor: \( 9 \times 2 = 18 \)
You need 18 teaspoons of the spice for the larger batch.
Problem 5: Photography
In photography, the aperture size affects the light entering the camera. If the f-number is 2.8 and changes to 5.6, how does the light change?
- The amount of light is proportional to the square of the f-number ratio: \( \left(\frac{5.6}{2.8}\right)^2 \)
- Calculate the ratio: \( 2^2 = 4 \)
The light entering the camera is reduced by a factor of 4.
These examples illustrate how squares and square roots are integral to solving diverse real-life problems in various fields.
Video hướng dẫn về lũy thừa và căn bậc hai từ Math Antics, giúp học sinh nắm vững các khái niệm toán học cơ bản.
Math Antics - Lũy Thừa và Căn Bậc Hai
READ MORE:
Video hướng dẫn bài tập về bình phương và căn bậc hai cho học sinh lớp 8 DAV, giúp học sinh nắm vững kiến thức toán học cơ bản.
Bài Tập 1 | Chương 1 | Toán Lớp 8 DAV | Bình Phương và Căn Bậc Hai | (CH01WS01) 🔥🔥🔥