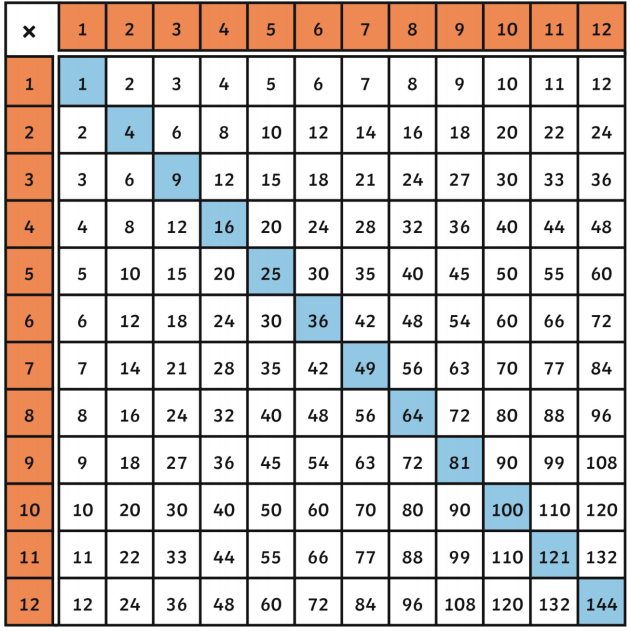
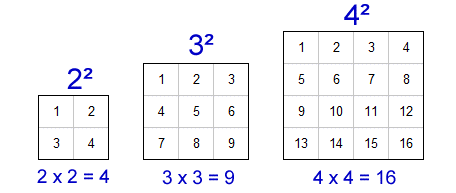
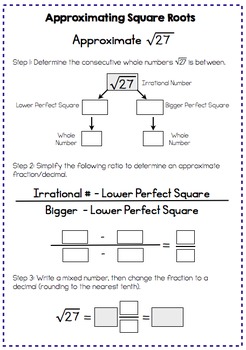
Topic approximate square root worksheet: Discover the art of estimating square roots with our comprehensive worksheet. Perfect for students and educators alike, this guide provides step-by-step instructions, practical examples, and engaging practice problems to enhance your mathematical skills. Learn to approximate non-perfect square roots effectively and boost your confidence in math. Start mastering square root approximations today!
Table of Content
- Approximating Square Roots Worksheet
- Introduction to Square Roots
- Understanding Perfect Squares
- Methods for Approximating Square Roots
- Estimating Square Roots without a Calculator
- Comparing Irrational Numbers with Radicals
- Approximating Square Roots on a Number Line
- Practice Problems and Solutions
- Advanced Techniques for Approximating Square Roots
- Using Numerical Methods to Approximate Square Roots
- Resources for Further Learning
- YOUTUBE: Hướng dẫn chi tiết về cách xấp xỉ căn bậc hai trong bài tập toán TEAS.
Approximating Square Roots Worksheet
Approximating square roots involves finding the nearest whole numbers between which the square root of a given number lies. This technique is useful for estimating the value of non-perfect squares. Below are detailed explanations and examples to help students understand and practice this concept.
Steps to Approximate Square Roots
- Identify the perfect squares between which the given number lies.
- Determine the whole numbers corresponding to these perfect squares.
- Estimate the square root based on the proximity of the given number to these perfect squares.
Example Problems
Let's find the approximate square root of 45.
- 45 is between 36 (62) and 49 (72).
- Thus, √45 is between 6 and 7.
- Since 45 is closer to 49, √45 is closer to 7. An estimation gives us approximately 6.7.
Practice Worksheet
Estimate the square roots of the following numbers without using a calculator. Fill in the blanks with two consecutive integers to complete the inequality:
- √50 is between ___ and ___
- √20 is between ___ and ___
- √75 is between ___ and ___
Advanced Practice
To challenge yourself further, try estimating the square roots to the nearest hundredth. For instance, approximate √45 to the hundredth place:
- Identify perfect squares: 36 (62) and 49 (72).
- Estimate: √45 ≈ 6.71 since it is closer to 7 than to 6.
Additional Resources
For more practice and in-depth explanations, consider exploring the following resources:
| Number | Perfect Squares | Estimated Square Root |
|---|---|---|
| 10 | 9, 16 | 3.2 |
| 26 | 25, 36 | 5.1 |
| 50 | 49, 64 | 7.1 |

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical concepts used in various fields, including algebra, geometry, and calculus. Understanding square roots helps in solving equations, analyzing geometric shapes, and simplifying mathematical expressions. This introduction will guide you through the basic definition, properties, and methods of approximating square roots.
The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). In mathematical notation, this is expressed as \( \sqrt{x} = y \). For example, the square root of 25 is 5 because \( 5^2 = 25 \).
Basic Properties of Square Roots
- Non-Negative Output: The square root of a non-negative number is always non-negative.
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25, whose square roots are integers.
- Product Property: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \).
- Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) where \( b \neq 0 \).
Approximating Square Roots
When dealing with numbers that are not perfect squares, we use methods to approximate the square root. Here are two common methods:
- Estimation Method: Identify the nearest perfect squares around the number. For example, to approximate \( \sqrt{50} \), note that 49 (7^2) and 64 (8^2) are the nearest perfect squares. Therefore, \( \sqrt{50} \) is slightly more than 7.
- Long Division Method: A more precise method involving a step-by-step division process, similar to traditional long division, but adapted for square roots.
Understanding these methods provides a solid foundation for more advanced mathematical problem-solving.
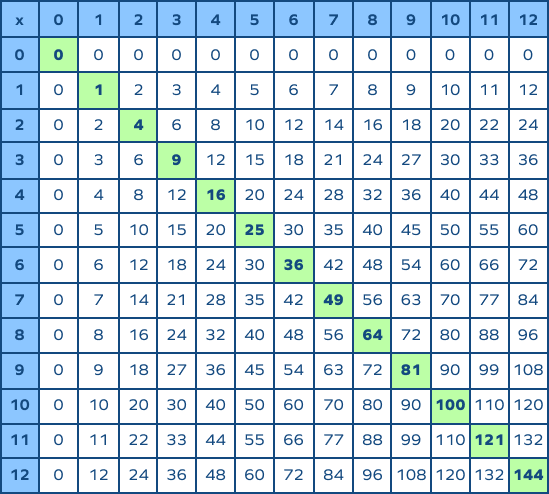
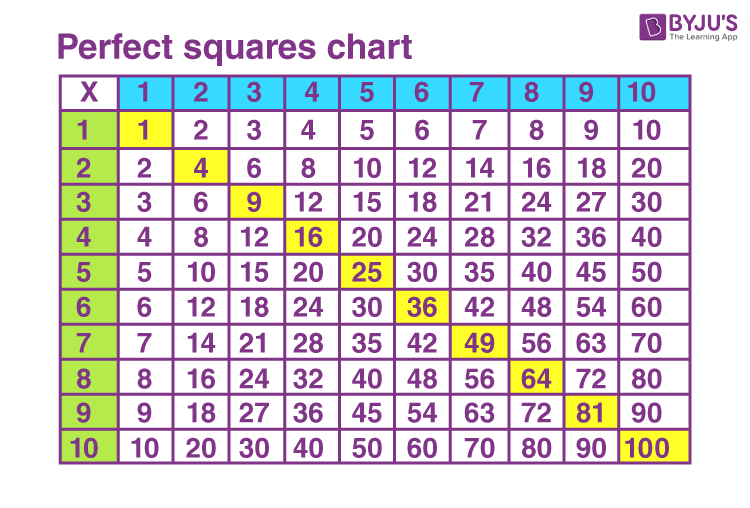
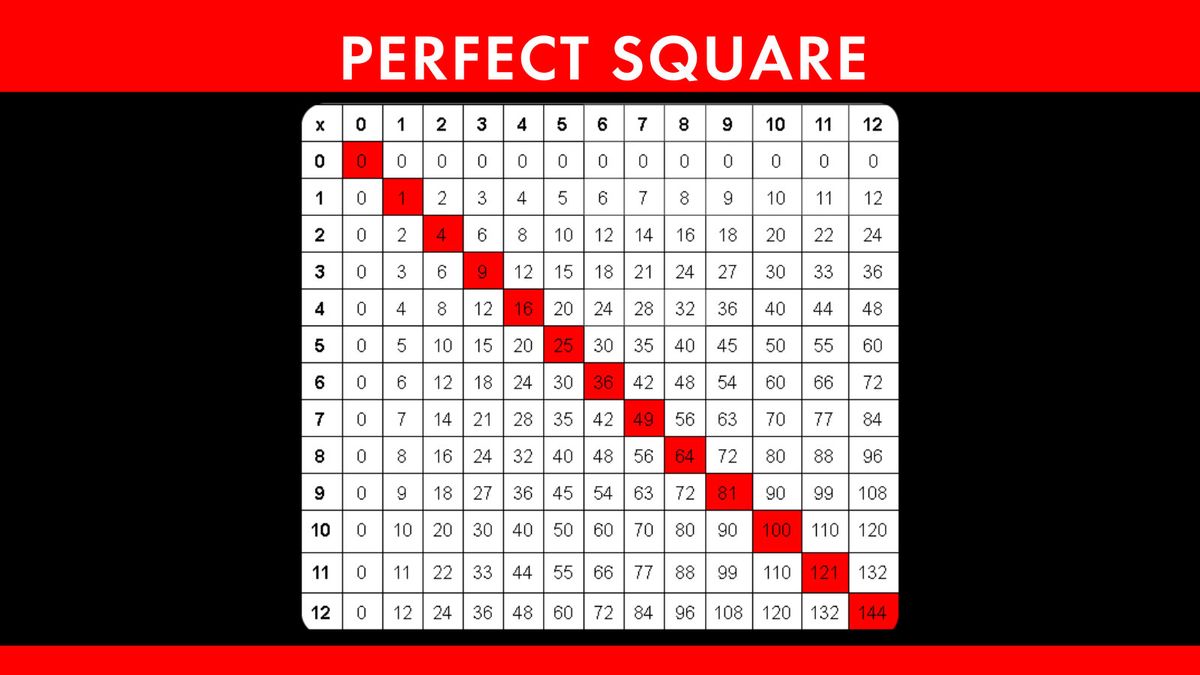
Understanding Perfect Squares
Perfect squares are numbers that are the result of squaring an integer. In other words, a perfect square is any number that can be expressed as \( n^2 \) where \( n \) is an integer.
For example:
- \(1 = 1^2\)
- \(4 = 2^2\)
- \(9 = 3^2\)
- \(16 = 4^2\)
- \(25 = 5^2\)
Understanding perfect squares is essential for simplifying square roots and for estimating the square roots of non-perfect squares. Recognizing perfect squares allows students to quickly determine the two integers between which the square root of a given number falls.
Here is a step-by-step approach to understanding and using perfect squares:
- Identify Perfect Squares: Memorize the list of perfect squares for integers 1 through at least 10 (e.g., 1, 4, 9, 16, 25, 36, 49, 64, 81, 100).
- Use Perfect Squares for Estimation: When given a number, determine which two perfect squares it falls between. For instance, the square root of 20 falls between the square root of 16 (which is 4) and the square root of 25 (which is 5).
- Approximate Square Roots: To approximate the square root of a non-perfect square, identify the closest perfect squares and estimate the value. For example, \( \sqrt{20} \) is approximately 4.5 because 20 is closer to 16 than to 25.
- Practice: Regular practice with worksheets and problems involving perfect squares and square roots can help reinforce these concepts and improve estimation skills.
By mastering perfect squares, students can more easily navigate problems involving square roots and gain a deeper understanding of number relationships in mathematics.
Methods for Approximating Square Roots
Approximating square roots can be accomplished through several methods, each offering a different level of accuracy and complexity. Here are some common techniques:
1. Estimation by Comparing with Known Squares
This method involves finding the two closest perfect squares that the number lies between and estimating the square root based on their values.
- Identify the perfect squares nearest to the number.
- Estimate the square root to be between the square roots of these perfect squares.
- Refine the estimate by considering how close the number is to each perfect square.
For example, to approximate \(\sqrt{50}\):
- Note that 50 is between 49 (which is \(7^2\)) and 64 (which is \(8^2\)).
- \(\sqrt{49} = 7\) and \(\sqrt{64} = 8\).
- Since 50 is closer to 49 than to 64, \(\sqrt{50}\) is slightly more than 7.
- An initial estimate might be around 7.1 or 7.2.
2. The Average Method
This iterative method involves making an initial guess and refining it using the average of the guess and the quotient of the number and the guess.
- Make an initial guess for the square root.
- Calculate the average of the guess and the number divided by the guess.
- Use this average as the new guess.
- Repeat until the guess is sufficiently accurate.
For example, to approximate \(\sqrt{50}\):
- Start with an initial guess, say 7.
- Calculate: \(\text{New guess} = \frac{7 + \frac{50}{7}}{2} \approx 7.071\).
- Repeat: \(\text{New guess} = \frac{7.071 + \frac{50}{7.071}}{2} \approx 7.071\).
- Continue until the guess stabilizes around 7.071.
3. Using the Binomial Theorem
The binomial theorem can provide a more precise approximation, particularly useful for numbers close to perfect squares.
For example, to approximate \(\sqrt{50}\):
- Rewrite 50 as \(49 + 1\).
- Use the approximation: \(\sqrt{49+1} \approx 7 + \frac{1}{2 \times 7} - \frac{1}{8 \times 7^3}\).
- Calculate: \(7 + \frac{1}{14} - \frac{1}{2744} \approx 7.071\).
4. Newton's Method (Heron's Method)
Newton's method provides a quick convergence to an accurate approximation.
- Choose an initial guess \(x_0\).
- Use the formula \(x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right)\), where \(S\) is the number whose square root is being approximated.
- Repeat until \(x_n\) converges to a stable value.
For example, to approximate \(\sqrt{50}\):
- Start with \(x_0 = 7\).
- Calculate \(x_1 = \frac{1}{2} \left( 7 + \frac{50}{7} \right) \approx 7.071\).
- Repeat: \(x_2 = \frac{1}{2} \left( 7.071 + \frac{50}{7.071} \right) \approx 7.071\).
- Continue until convergence, typically \(x_2\) or \(x_3\) is accurate enough.
Estimating Square Roots without a Calculator
Estimating square roots without a calculator involves a few simple steps to get an approximation. Here's a detailed step-by-step guide:
-
Identify the Perfect Squares:
First, determine the two perfect squares between which your number lies. For example, to estimate \( \sqrt{50} \), note that \( 7^2 = 49 \) and \( 8^2 = 64 \). So, \( \sqrt{50} \) lies between 7 and 8.
-
Initial Approximation:
Start with the smaller perfect square root. In our example, begin with 7. Divide the number by this approximation:
\[
\frac{50}{7} \approx 7.14
\] -
Average the Results:
Take the average of the initial approximation and the result of the division:
\[
\text{Average} = \frac{7 + 7.14}{2} \approx 7.07
\] -
Repeat for Better Accuracy:
Repeat the division and averaging process with the new approximation:
\[
\frac{50}{7.07} \approx 7.07
\]\[
\text{Average} = \frac{7.07 + 7.07}{2} \approx 7.07
\]Since the new result is quite close to the previous approximation, \( \sqrt{50} \approx 7.07 \).
Using this method, you can iteratively refine your estimate. The process can be repeated until the desired level of accuracy is achieved.
Here's another example for clarity:
-
Example for \( \sqrt{20} \):
Identify perfect squares: 4 and 5 since \( 4^2 = 16 \) and \( 5^2 = 25 \).
-
Initial Approximation:
Start with 4:
\[
\frac{20}{4} = 5
\] -
Average the Results:
\[
\text{Average} = \frac{4 + 5}{2} = 4.5
\] -
Repeat for Better Accuracy:
Repeat with 4.5:
\[
\frac{20}{4.5} \approx 4.44
\]\[
\text{Average} = \frac{4.5 + 4.44}{2} \approx 4.47
\]Thus, \( \sqrt{20} \approx 4.47 \).
By using this method, you can estimate the square roots of various numbers without a calculator, which is particularly useful in many practical applications.
Comparing Irrational Numbers with Radicals
When working with irrational numbers and radicals, it's essential to understand their properties and how they compare to each other. Here is a step-by-step guide:
-
Definition of Irrational Numbers:
An irrational number cannot be expressed as a simple fraction. Examples include \( \pi \) and \( \sqrt{2} \). These numbers have non-repeating, non-terminating decimal expansions.
-
Understanding Radicals:
Radicals are symbols used to denote roots, such as square roots or cube roots. The most common radical is the square root, denoted by \( \sqrt{} \).
- \( \sqrt{2} \approx 1.414 \)
- \( \sqrt{3} \approx 1.732 \)
- \( \sqrt{5} \approx 2.236 \)
-
Comparison Methods:
To compare irrational numbers with radicals, follow these steps:
- Estimate the Values: Approximate the value of each radical. For example, \( \sqrt{2} \approx 1.414 \) and \( \pi \approx 3.141 \).
- Place on a Number Line: Plot the approximated values on a number line to visually compare them.
- Calculate Differences: For a more precise comparison, calculate the difference between the values. For instance, \( \pi - \sqrt{2} \approx 1.727 \).
-
Practical Examples:
Let's compare \( \sqrt{2} \) and \( \sqrt{3} \):
\[
\sqrt{2} \approx 1.414 \quad \text{and} \quad \sqrt{3} \approx 1.732
\]Since \( 1.732 > 1.414 \), we see that \( \sqrt{3} \) is greater than \( \sqrt{2} \).
-
Applications:
Comparing irrational numbers is useful in various mathematical contexts, such as determining the lengths of sides in geometric figures or solving algebraic equations involving roots.
By following these steps, you can effectively compare irrational numbers and radicals, enhancing your understanding and problem-solving skills in mathematics.
Approximating Square Roots on a Number Line
Approximating square roots on a number line involves visualizing and estimating where a square root lies between two perfect squares. Here are the steps to approximate square roots using a number line:
-
Identify the nearest perfect squares: Determine the two perfect squares between which the given number lies. For example, to approximate \( \sqrt{20} \), note that \( 16 \) and \( 25 \) are perfect squares close to \( 20 \) because \( 4^2 = 16 \) and \( 5^2 = 25 \).
-
Locate the approximate position: Place the number on a number line between the identified perfect squares. \( 20 \) is closer to \( 16 \) than to \( 25 \), so \( \sqrt{20} \) will be slightly greater than 4 but less than 5.
-
Refine the approximation: Use the midpoint to refine your estimate. The midpoint between \( 4 \) and \( 5 \) is \( 4.5 \). Check:
- \( 4.5^2 = 20.25 \), which is very close to \( 20 \), so \( \sqrt{20} \approx 4.5 \).
Verify with smaller intervals: If more precision is needed, consider smaller intervals. For example, test between \( 4.4 \) and \( 4.6 \).
- \( 4.4^2 = 19.36 \)
- \( 4.6^2 = 21.16 \)
Since \( 20 \) is closer to \( 19.36 \) than to \( 21.16 \), we refine our estimate to \( 4.4 \) to \( 4.5 \). Continue this process to achieve the desired accuracy.
Here is an example table to help visualize these steps:
| Number | Perfect Squares | Approximate Root | Refined Estimate |
|---|---|---|---|
| 20 | 16 (4²) and 25 (5²) | 4.5 | 4.4 to 4.5 |
| 50 | 49 (7²) and 64 (8²) | 7.1 | 7.05 to 7.1 |
By following these steps and refining your estimates, you can approximate square roots on a number line effectively without the need for a calculator.
Practice Problems and Solutions
Here are some practice problems to help you understand and master the approximation of square roots. Try to solve them on your own and then check the solutions provided.
Problem Set 1
- Approximate the square root of 10.
- Estimate the square root of 50.
- Find the square root of 75 to the nearest tenth.
- Approximate the square root of 120.
- Estimate the square root of 200.
Solutions
-
Square root of 10:
We know that \(3^2 = 9\) and \(4^2 = 16\). Therefore, \(\sqrt{10}\) is between 3 and 4.
By trying midpoints: \(3.2^2 = 10.24\), so \(\sqrt{10} \approx 3.2\).
-
Square root of 50:
We know that \(7^2 = 49\) and \(8^2 = 64\). Therefore, \(\sqrt{50}\) is slightly more than 7.
By trying midpoints: \(7.1^2 = 50.41\), so \(\sqrt{50} \approx 7.1\).
-
Square root of 75:
We know that \(8^2 = 64\) and \(9^2 = 81\). Therefore, \(\sqrt{75}\) is between 8 and 9.
By trying midpoints: \(8.7^2 = 75.69\), so \(\sqrt{75} \approx 8.7\).
-
Square root of 120:
We know that \(10^2 = 100\) and \(11^2 = 121\). Therefore, \(\sqrt{120}\) is slightly less than 11.
By trying midpoints: \(10.95^2 = 119.90\), so \(\sqrt{120} \approx 10.95\).
-
Square root of 200:
We know that \(14^2 = 196\) and \(15^2 = 225\). Therefore, \(\sqrt{200}\) is slightly more than 14.
By trying midpoints: \(14.1^2 = 198.81\), so \(\sqrt{200} \approx 14.1\).
Problem Set 2
- Approximate the square root of 30.
- Estimate the square root of 60.
- Find the square root of 90 to the nearest tenth.
- Approximate the square root of 150.
- Estimate the square root of 250.
Solutions
-
Square root of 30:
We know that \(5^2 = 25\) and \(6^2 = 36\). Therefore, \(\sqrt{30}\) is between 5 and 6.
By trying midpoints: \(5.5^2 = 30.25\), so \(\sqrt{30} \approx 5.5\).
-
Square root of 60:
We know that \(7^2 = 49\) and \(8^2 = 64\). Therefore, \(\sqrt{60}\) is slightly less than 8.
By trying midpoints: \(7.7^2 = 59.29\), so \(\sqrt{60} \approx 7.7\).
-
Square root of 90:
We know that \(9^2 = 81\) and \(10^2 = 100\). Therefore, \(\sqrt{90}\) is slightly more than 9.
By trying midpoints: \(9.5^2 = 90.25\), so \(\sqrt{90} \approx 9.5\).
-
Square root of 150:
We know that \(12^2 = 144\) and \(13^2 = 169\). Therefore, \(\sqrt{150}\) is between 12 and 13.
By trying midpoints: \(12.2^2 = 148.84\), so \(\sqrt{150} \approx 12.2\).
-
Square root of 250:
We know that \(15^2 = 225\) and \(16^2 = 256\). Therefore, \(\sqrt{250}\) is slightly less than 16.
By trying midpoints: \(15.8^2 = 249.64\), so \(\sqrt{250} \approx 15.8\).
Advanced Techniques for Approximating Square Roots
Approximating square roots can be enhanced using advanced techniques. Here, we explore several methods:
1. Newton's Method
Newton's Method, also known as the Newton-Raphson method, is an iterative approach to finding successively better approximations to the roots of a real-valued function.
- Choose an initial approximation \( x_0 \).
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \) to find the next approximation.
- Repeat the process until the desired level of accuracy is achieved.
For example, to approximate \( \sqrt{10} \):
- Let \( x_0 = 3 \).
- Then \( x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667 \).
- Next, \( x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) = 3.1623 \).
- Continue this process to improve the approximation.
2. Long Division Method
The long division method provides a more precise approximation but is more tedious.
- Group the digits in pairs, starting from the decimal point.
- Find the largest number whose square is less than or equal to the first group. This is the initial quotient.
- Subtract the square of the quotient from the first group, bring down the next pair of digits, and continue the process.
This method involves detailed calculations that can provide a highly accurate result.
3. Using the Approximation Formula
This formula approximates the square root by expressing the number as the sum of a perfect square and a small remainder.
- Let \( n \) be the number and \( n = p + q \) where \( p \) is the nearest perfect square less than \( n \) and \( q \) is the remainder.
- The approximation formula is: \( \sqrt{n} \approx \sqrt{p} + \frac{q}{2\sqrt{p} + 1} \).
For example, to approximate \( \sqrt{968} \):
- Identify \( p = 961 \) (since \( 31^2 = 961 \) and \( 32^2 = 1024 \)).
- Then \( q = 968 - 961 = 7 \).
- Apply the formula: \( \sqrt{968} \approx 31 + \frac{7}{2 \times 31 + 1} = 31 + \frac{7}{63} \approx 31.11 \).
These methods provide various levels of precision and complexity, allowing for different applications depending on the required accuracy and computational resources available.

Using Numerical Methods to Approximate Square Roots
Numerical methods for approximating square roots can be highly effective, especially for obtaining accurate results without the use of a calculator. Below are some common techniques explained step-by-step:
1. Newton's Method (or the Newton-Raphson Method)
This iterative method provides a quick approximation of the square root. Here’s how it works:
- Start with an initial guess \( x_0 \). A good starting point can be the number divided by 2.
- Use the iterative formula: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \] where \( S \) is the number whose square root you are trying to find, and \( x_n \) is the current approximation.
- Repeat the process until the difference between \( x_{n+1} \) and \( x_n \) is smaller than a desired tolerance level (e.g., 0.0001).
Example:
To find \(\sqrt{10}\):
- Initial guess: \( x_0 = 5 \)
- First iteration: \[ x_1 = \frac{1}{2} \left( 5 + \frac{10}{5} \right) = 3.5 \]
- Second iteration: \[ x_2 = \frac{1}{2} \left( 3.5 + \frac{10}{3.5} \right) \approx 3.1786 \]
- Third iteration: \[ x_3 = \frac{1}{2} \left( 3.1786 + \frac{10}{3.1786} \right) \approx 3.1623 \]
- Continue until the desired precision is reached.
2. The Babylonian Method (similar to Newton's Method)
This ancient method also uses an iterative approach:
- Start with an initial guess \( x_0 \).
- Use the iterative formula: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \]
- Repeat until convergence.
Example:
To find \(\sqrt{25}\):
- Initial guess: \( x_0 = 12.5 \) (just half of 25)
- First iteration: \[ x_1 = \frac{1}{2} \left( 12.5 + \frac{25}{12.5} \right) = 7.25 \]
- Second iteration: \[ x_2 = \frac{1}{2} \left( 7.25 + \frac{25}{7.25} \right) \approx 5.3491 \]
- Third iteration: \[ x_3 = \frac{1}{2} \left( 5.3491 + \frac{25}{5.3491} \right) \approx 5.0114 \]
- Fourth iteration: \[ x_4 = \frac{1}{2} \left( 5.0114 + \frac{25}{5.0114} \right) \approx 5.0000 \]
- Thus, \(\sqrt{25} \approx 5.0000\).
3. Bisection Method
This method involves finding the midpoint of the interval and determining whether the square root lies in the left or right subinterval:
- Choose an interval \([a, b]\) such that \(a^2 \leq S \leq b^2\).
- Find the midpoint \( m = \frac{a + b}{2} \).
- Check:
- If \(m^2 < S\), then set \( a = m \).
- If \(m^2 > S\), then set \( b = m \).
- Repeat until the interval \([a, b]\) is sufficiently small.
Example:
To find \(\sqrt{20}\):
- Initial interval: \([4, 5]\)
- First midpoint: \[ m = \frac{4 + 5}{2} = 4.5 \]
- Check: \[ 4.5^2 = 20.25 \quad (\text{since } 20.25 > 20, \text{ set } b = 4.5) \]
- Next midpoint: \[ m = \frac{4 + 4.5}{2} = 4.25 \]
- Continue until the interval is sufficiently small.
Resources for Further Learning
To further enhance your understanding of approximating square roots and related mathematical concepts, consider exploring the following resources:
-
Online Courses and Tutorials:
-
Books and Publications:
- "Algebra and Trigonometry" by Robert F. Blitzer
- "Precalculus: Mathematics for Calculus" by James Stewart, Lothar Redlin, and Saleem Watson
- "The Art of Problem Solving, Volume 1: The Basics" by Sandor Lehoczky and Richard Rusczyk
-
Interactive Tools and Calculators:
-
Worksheets and Practice Problems:
Hướng dẫn chi tiết về cách xấp xỉ căn bậc hai trong bài tập toán TEAS.
Mẹo Làm Bài Tập Toán TEAS - Video 8 - Xấp Xỉ Căn Bậc Hai
READ MORE:
Hướng dẫn cách tìm căn bậc hai xấp xỉ của một số mà không cần sử dụng máy tính.
Tìm Căn Bậc Hai Xấp Xỉ Của Một Số Mà Không Cần Máy Tính