Topic what are the first 10 perfect square numbers: Curious about perfect squares? This article will guide you through the first 10 perfect square numbers, explaining their significance and applications in mathematics. Perfect for students, educators, and math enthusiasts, our comprehensive guide will help you understand and appreciate these fundamental numbers.
Table of Content
- Understanding Perfect Square Numbers
- Introduction to Perfect Squares
- Definition and Properties of Perfect Squares
- Importance of Perfect Squares in Mathematics
- List of the First 10 Perfect Square Numbers
- Calculation Method for Perfect Squares
- Visual Representation of Perfect Squares
- Applications of Perfect Squares in Real Life
- Perfect Squares and Algebra
- Perfect Squares in Geometry
- Common Mistakes and Misconceptions About Perfect Squares
- Practice Problems and Solutions
- Conclusion and Further Reading
- YOUTUBE:
Understanding Perfect Square Numbers
In mathematics, a perfect square is an integer that can be expressed as the product of another integer with itself. In other words, a number n is a perfect square if there exists an integer m such that n = m^2.
The First 10 Perfect Square Numbers
The first 10 perfect square numbers are as follows:
- \(1 = 1^2\)
- \(4 = 2^2\)
- \(9 = 3^2\)
- \(16 = 4^2\)
- \(25 = 5^2\)
- \(36 = 6^2\)
- \(49 = 7^2\)
- \(64 = 8^2\)
- \(81 = 9^2\)
- \(100 = 10^2\)
Properties of Perfect Squares
- A perfect square always ends in 0, 1, 4, 5, 6, or 9.
- The square root of a perfect square is always an integer.
- Perfect squares can be positive, and their square roots can be either positive or negative.
- If a number ends in 2, 3, 7, or 8, it is not a perfect square.
Examples of Perfect Squares in Use
Perfect squares are useful in various mathematical contexts, such as geometry, where the area of a square is the square of its side length. They also appear in algebraic formulas and can be used to simplify calculations.
Interesting Facts
- The difference between successive perfect squares increases by 2 each time. For example, \(4 - 1 = 3\), \(9 - 4 = 5\), \(16 - 9 = 7\), and so on.
- Squares of even numbers are even, and squares of odd numbers are odd.
Conclusion
Understanding perfect squares is fundamental in mathematics, providing a foundation for more advanced topics. Recognizing and utilizing these numbers can simplify many mathematical problems and concepts.
For further reading and tools to generate lists of perfect squares, you can visit online resources and calculators designed to explore these fascinating numbers in more depth.
READ MORE:
Introduction to Perfect Squares
Perfect squares are numbers that can be expressed as the product of an integer multiplied by itself. These numbers are fundamental in various branches of mathematics, including algebra and geometry. Understanding perfect squares can help in solving equations, simplifying expressions, and analyzing geometric shapes.
The first 10 perfect square numbers are:
- \(1^2 = 1\)
- \(2^2 = 4\)
- \(3^2 = 9\)
- \(4^2 = 16\)
- \(5^2 = 25\)
- \(6^2 = 36\)
- \(7^2 = 49\)
- \(8^2 = 64\)
- \(9^2 = 81\)
- \(10^2 = 100\)
In general, a perfect square can be written as \(n^2\), where \(n\) is an integer. For example, \(4\) is a perfect square because it can be written as \(2^2\), and \(25\) is a perfect square because it can be written as \(5^2\).
Perfect squares have distinctive properties that make them unique:
- They are always non-negative.
- The number of factors for a perfect square is always odd.
- Perfect squares always end in 0, 1, 4, 5, 6, or 9 in base 10.
Exploring perfect squares provides a foundation for more advanced mathematical concepts and problem-solving techniques. Whether you are a student or a math enthusiast, mastering the concept of perfect squares is essential for your mathematical journey.
Definition and Properties of Perfect Squares
A perfect square is a number that can be expressed as the product of an integer with itself. In mathematical terms, if \(n\) is an integer, then \(n^2\) is a perfect square. For example, \(9\) is a perfect square because it can be written as \(3^2\).
Here are the first 10 perfect square numbers and their corresponding integers:
| \(1^2\) | = | 1 |
| \(2^2\) | = | 4 |
| \(3^2\) | = | 9 |
| \(4^2\) | = | 16 |
| \(5^2\) | = | 25 |
| \(6^2\) | = | 36 |
| \(7^2\) | = | 49 |
| \(8^2\) | = | 64 |
| \(9^2\) | = | 81 |
| \(10^2\) | = | 100 |
Perfect squares have several interesting properties:
- They are always non-negative. Since both positive and negative numbers, when squared, give a non-negative result, perfect squares are always non-negative.
- They have an odd number of total factors. For instance, \(36\) has the factors \(1, 2, 3, 4, 6, 9, 12, 18, 36\) which amounts to 9 factors.
- They end in specific digits in base 10. A perfect square can only end in 0, 1, 4, 5, 6, or 9. This helps in quickly identifying whether a number is a perfect square or not.
- Every perfect square is the sum of consecutive odd numbers. For example, \(1 + 3 + 5 = 9\) which is \(3^2\).
Understanding these properties can help in recognizing and working with perfect squares more effectively in various mathematical problems.
Importance of Perfect Squares in Mathematics
Perfect squares play a crucial role in various fields of mathematics due to their unique properties and applications. Understanding perfect squares is fundamental to mastering several mathematical concepts and techniques. Here are some key reasons why perfect squares are important:
- Algebraic Simplification: Perfect squares are used to simplify algebraic expressions. For instance, the expression \((a+b)^2\) can be expanded to \(a^2 + 2ab + b^2\).
- Solving Quadratic Equations: Perfect squares are integral to solving quadratic equations. Completing the square is a common method used to solve equations of the form \(ax^2 + bx + c = 0\).
- Number Theory: In number theory, perfect squares are used to study the properties of integers. For example, Fermat's theorem on sums of two squares involves identifying numbers that can be expressed as the sum of two perfect squares.
- Geometry: Perfect squares are fundamental in geometry. The area of a square is a perfect square, given by the formula \(s^2\) where \(s\) is the length of a side. Additionally, the Pythagorean theorem involves perfect squares in calculating the lengths of sides of right triangles.
- Patterns and Sequences: Perfect squares appear in various mathematical sequences and patterns. The sequence of perfect squares (1, 4, 9, 16, ...) is one of the most well-known numerical sequences.
- Diophantine Equations: These are polynomial equations that require integer solutions. Many Diophantine equations involve perfect squares, such as the famous equation \(x^2 - Ny^2 = 1\).
To illustrate the significance of perfect squares, consider the following examples:
| Application | Example |
| Algebraic Identity | \((x + 3)^2 = x^2 + 6x + 9\) |
| Pythagorean Theorem | \(3^2 + 4^2 = 5^2\) |
| Quadratic Equation | \(x^2 - 4x + 4 = 0\) can be solved by recognizing \((x-2)^2 = 0\) |
Understanding and applying perfect squares enables students and mathematicians to solve complex problems, recognize patterns, and appreciate the beauty of mathematical structures. Their importance cannot be overstated, as they form the foundation for many advanced mathematical concepts and techniques.
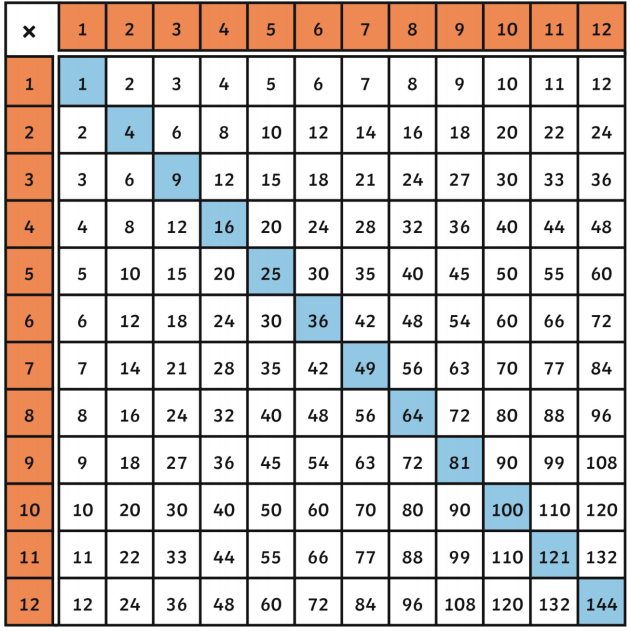
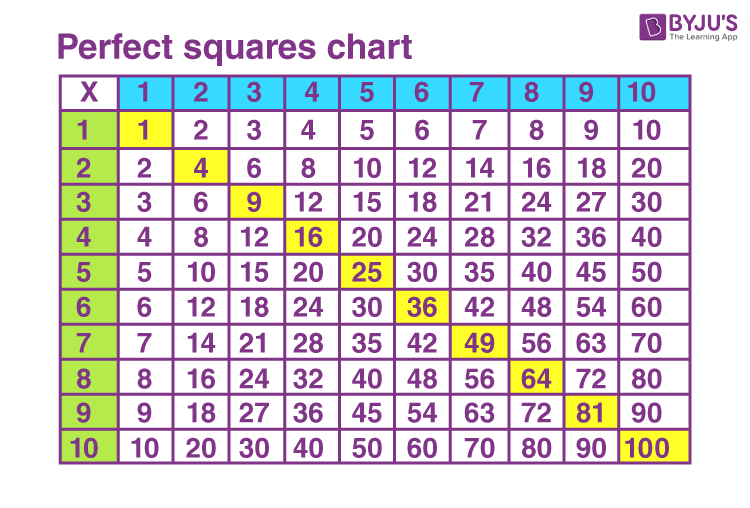
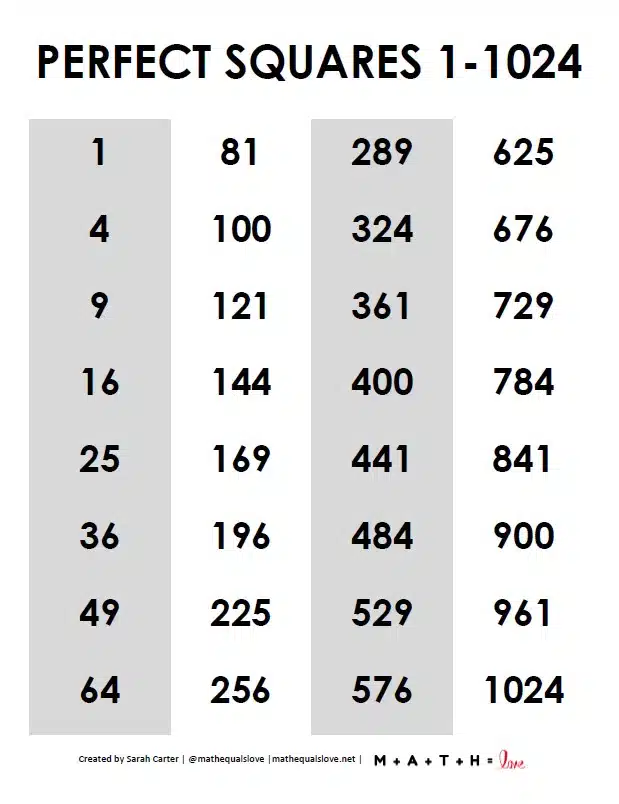
List of the First 10 Perfect Square Numbers
Perfect squares are the squares of integers. They are the result of an integer multiplied by itself. Below is a list of the first 10 perfect square numbers, along with their corresponding integers:
| Integer (n) | Perfect Square (n2) |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
The process of squaring an integer is simple: multiply the integer by itself. For example:
- The square of 1 is \(1 \times 1 = 1\).
- The square of 2 is \(2 \times 2 = 4\).
- The square of 3 is \(3 \times 3 = 9\).
- The square of 4 is \(4 \times 4 = 16\).
- The square of 5 is \(5 \times 5 = 25\).
- The square of 6 is \(6 \times 6 = 36\).
- The square of 7 is \(7 \times 7 = 49\).
- The square of 8 is \(8 \times 8 = 64\).
- The square of 9 is \(9 \times 9 = 81\).
- The square of 10 is \(10 \times 10 = 100\).
These first 10 perfect square numbers are fundamental in mathematics and form the basis for more complex concepts and operations. Understanding these basic perfect squares is crucial for solving various mathematical problems and for further study in algebra and geometry.

Calculation Method for Perfect Squares
Calculating perfect squares is a straightforward process that involves multiplying an integer by itself. Here are the steps to find the perfect square of an integer:
- Select an integer \(n\).
- Multiply the integer by itself: \(n \times n\).
- The result is the perfect square: \(n^2\).
Let's go through the calculation method with an example:
- Choose the integer \(4\).
- Multiply \(4\) by itself: \(4 \times 4\).
- The result is \(16\), so \(16\) is the perfect square of \(4\).
We can generalize this process for any integer \(n\). The formula to calculate a perfect square is:
\[ n^2 = n \times n \]
Here are the calculations for the first 10 perfect squares:
| Integer (n) | Calculation | Perfect Square (n2) |
| 1 | 1 × 1 | 1 |
| 2 | 2 × 2 | 4 |
| 3 | 3 × 3 | 9 |
| 4 | 4 × 4 | 16 |
| 5 | 5 × 5 | 25 |
| 6 | 6 × 6 | 36 |
| 7 | 7 × 7 | 49 |
| 8 | 8 × 8 | 64 |
| 9 | 9 × 9 | 81 |
| 10 | 10 × 10 | 100 |
By following these simple steps, you can easily calculate the perfect square of any integer. This method is fundamental in mathematics and is widely used in various mathematical applications and problem-solving scenarios.
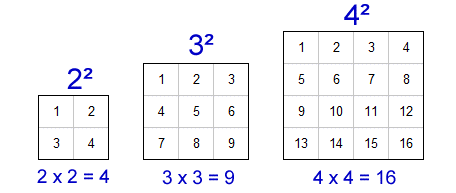
Visual Representation of Perfect Squares
Perfect squares are numbers that are the square of integers. Visualizing these numbers can help in understanding their properties and applications better. Below is a representation of the first 10 perfect square numbers along with their square roots.
| Number | Perfect Square | Visual Representation |
|---|---|---|
| 1 | 1 | |
| 2 | 4 | |
| 3 | 9 | |
| 4 | 16 | |
| 5 | 25 | |
| 6 | 36 | |
| 7 | 49 | |
| 8 | 64 | |
| 9 | 81 | |
| 10 | 100 |
The table above lists the first 10 perfect squares and shows their mathematical representation. Each perfect square is the product of an integer with itself. Understanding this concept is fundamental in various branches of mathematics.
Applications of Perfect Squares in Real Life
Perfect squares play a significant role in various real-life applications due to their unique properties. Below are some practical uses of perfect squares:
-
Architecture and Design:
Perfect squares are essential in architectural design and construction. When designing buildings and rooms, architects often use square areas to ensure symmetry and balance. For instance, a square courtyard or room maximizes space efficiency and provides an aesthetically pleasing structure.
-
Landscaping and Agriculture:
In landscaping, perfect squares are used to design garden plots, lawns, and other outdoor spaces. This ensures uniformity and easy maintenance. Similarly, in agriculture, farmers use square plots to optimize the use of land and resources for planting crops.
-
Technology and Computing:
Perfect squares are used in computing algorithms, particularly in graphics and image processing. For example, pixels in digital screens are often arranged in square grids to ensure uniform resolution and clarity.
-
Education and Learning:
Perfect squares are fundamental in teaching various mathematical concepts, including multiplication, area calculation, and square roots. They help students understand and visualize mathematical relationships and patterns.
-
Sports and Recreation:
Many sports fields and courts, such as basketball and volleyball courts, are designed using perfect square dimensions to ensure standardization and fairness in gameplay.
-
Art and Quilting:
In art, perfect squares are used in patterns and designs to create visually appealing compositions. Quilters often use square patches to create intricate and beautiful quilts.
These examples illustrate the versatility and importance of perfect squares in various domains. Their application extends beyond theoretical mathematics into practical, everyday use, highlighting the integral role they play in our lives.
Perfect Squares and Algebra
Perfect squares play a significant role in algebra. Here are some key points and applications:
- Quadratic Equations: Perfect squares frequently appear in quadratic equations. For example, the quadratic equation \(x^2 - 6x + 9 = 0\) can be factored as \((x - 3)^2 = 0\), showing that the solution is \(x = 3\).
- Completing the Square: This is a method used to solve quadratic equations. By converting a quadratic equation into a perfect square trinomial, we can solve for the variable more easily. For instance, the equation \(x^2 + 4x + 4 = 0\) is a perfect square trinomial because it can be written as \((x + 2)^2 = 0\).
- Graphing Parabolas: The vertex form of a parabola, \(y = a(x - h)^2 + k\), involves a perfect square. This form makes it easier to graph the parabola by identifying its vertex at \((h, k)\).
- Inequalities: Perfect squares are used to solve inequalities involving quadratic expressions. For example, solving \(x^2 < 9\) involves recognizing that \(x^2 = 9\) has solutions \(x = \pm 3\), and thus the inequality holds for \(-3 < x < 3\).
Perfect squares are also essential in various algebraic identities and formulas:
- \((a + b)^2 = a^2 + 2ab + b^2\)
- \((a - b)^2 = a^2 - 2ab + b^2\)
- \(a^2 - b^2 = (a + b)(a - b)\)
These identities simplify the process of expanding and factoring expressions.
Additionally, in the context of algebra, recognizing perfect squares can help simplify radical expressions and solve equations involving square roots. For instance, knowing that \( \sqrt{25} = 5\) helps in simplifying expressions like \( \sqrt{100x^2} = 10|x| \).
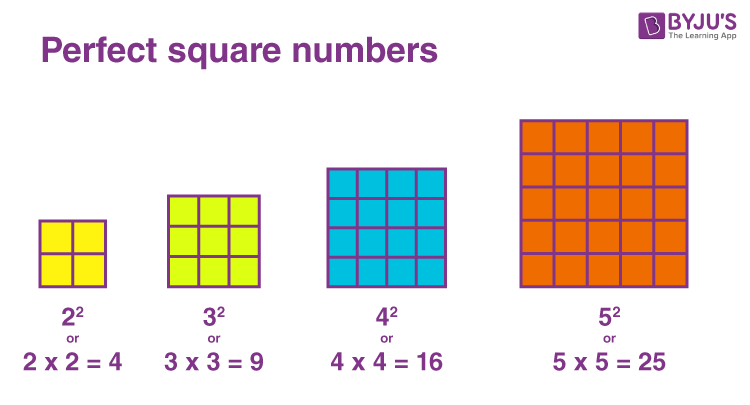
Perfect Squares in Geometry
Perfect squares have significant applications in geometry, especially in understanding shapes, areas, and distances. Below are some key applications:
-
Area Calculation:
In geometry, the concept of area often involves perfect squares. For example, the area of a square with side length \(s\) is given by the formula \(A = s^2\). This shows that the area is a perfect square.
-
Pythagorean Theorem:
The Pythagorean theorem is a fundamental principle in geometry that involves perfect squares. It states that in a right triangle, the square of the hypotenuse (\(c\)) is equal to the sum of the squares of the other two sides (\(a\) and \(b\)): \[c^2 = a^2 + b^2\]
-
Distance Formula:
The distance between two points in a plane can be calculated using the distance formula, which involves perfect squares. For points \((x_1, y_1)\) and \((x_2, y_2)\), the distance \(d\) is given by:
\[d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\] -
Coordinate Geometry:
In coordinate geometry, perfect squares are used to find the lengths of segments and to solve equations involving circles, parabolas, and other conic sections. For example, the equation of a circle with radius \(r\) centered at \((h, k)\) is:
\[(x - h)^2 + (y - k)^2 = r^2\] -
Volume and Surface Area:
When dealing with three-dimensional shapes, perfect squares help in calculating volume and surface area. For instance, the surface area of a cube with side length \(a\) is:
\[A = 6a^2\]
and its volume is:
\[V = a^3\]
Understanding perfect squares in geometry helps in solving problems related to shapes, distances, and spatial reasoning, making it a crucial concept in both basic and advanced geometry.
Common Mistakes and Misconceptions About Perfect Squares
Perfect squares, while straightforward in concept, often lead to common mistakes and misconceptions among students. Understanding these can help in avoiding errors and gaining a clearer grasp of the subject.
- Misidentifying Non-Perfect Squares: A common mistake is assuming that any integer result from a square root calculation indicates a perfect square. However, the result must be a whole number. For example, \( \sqrt{24} = 4.89 \) is not a whole number, so 24 is not a perfect square.
- Perfect Squares and Negative Numbers: Some may think that negative numbers can be perfect squares. However, perfect squares are always non-negative because both positive and negative numbers squared result in positive values. For instance, \( (-3)^2 = 9 \) and \( 3^2 = 9 \), but no number squared equals a negative number.
- Units Digit Confusion: Students often get confused by the units digit of perfect squares. A number ending in 2, 3, 7, or 8 is never a perfect square. Understanding this pattern helps in quickly identifying non-perfect squares. For example, 23 and 37 cannot be perfect squares because their units digits do not match the expected pattern.
- Even and Odd Perfect Squares: Another common misconception is that the square of an even number is odd or vice versa. In reality, the square of an even number is always even, and the square of an odd number is always odd. For instance, \( 6^2 = 36 \) (even) and \( 7^2 = 49 \) (odd).
- Prime Factorization: Perfect squares have an even power of all their prime factors. Students may forget to check this, leading to incorrect assumptions. For example, \( 36 = 2^2 \times 3^2 \) is a perfect square, whereas \( 18 = 2^1 \times 3^2 \) is not, as 2 is raised to an odd power.
Recognizing these common mistakes can significantly improve understanding and performance in mathematical problems involving perfect squares.
Practice Problems and Solutions
Here are some practice problems to help reinforce the concept of perfect squares. Try solving them on your own before checking the solutions provided.
-
Find the perfect square of 7.
Solution: To find the perfect square of 7, we multiply 7 by itself:
\[7 \times 7 = 49\]
Thus, the perfect square of 7 is 49.
-
Determine whether 50 is a perfect square.
Solution: To check if 50 is a perfect square, find its square root:
\[\sqrt{50} \approx 7.071\]
Since the square root is not a whole number, 50 is not a perfect square.
-
What is the next perfect square after 64?
Solution: The square root of 64 is 8. The next whole number is 9, so the next perfect square is:
\[9 \times 9 = 81\]
Thus, the next perfect square after 64 is 81.
-
If the area of a square is 121 square units, what is the length of one side?
Solution: The area of a square is given by the side length squared. Thus, to find the side length:
\[\sqrt{121} = 11\]
Therefore, the length of one side of the square is 11 units.
-
Find the smallest number that needs to be added to 75 to make it a perfect square.
Solution: The nearest perfect square greater than 75 is 81 (since \[9 \times 9 = 81\]). Therefore:
\[81 - 75 = 6\]
Thus, 6 is the smallest number that needs to be added to 75 to make it a perfect square.
These practice problems cover basic concepts of perfect squares and help strengthen understanding through real-world examples. Keep practicing to master perfect squares!
Conclusion and Further Reading
Perfect squares are fundamental concepts in mathematics, providing a foundation for various applications in algebra, geometry, and real-life scenarios. Understanding perfect squares helps in solving quadratic equations, analyzing geometric shapes, and interpreting data in a structured manner. They also appear frequently in mathematical proofs and problem-solving techniques.
We have explored the definition, properties, and significance of perfect squares, along with their applications in different areas. To delve deeper into this topic, here are some recommended readings:
- - This resource provides detailed explanations and examples of perfect squares and their applications.
- - This article offers a thorough overview of perfect squares, including lists, charts, and solved examples.
- - Explore algebraic concepts related to perfect squares and practice problems to enhance your understanding.
- - A simple and engaging explanation of perfect squares, suitable for all age groups.
By exploring these resources, you can strengthen your knowledge of perfect squares and their crucial role in mathematics. Happy learning!
Số Chính Phương và Căn Bậc Hai (1-10) | 10 Số Chính Phương Đầu Tiên & Căn Bậc Hai | Toán Học với Thầy J
READ MORE:
Những Số Chính Phương Đầu Tiên Là Gì?