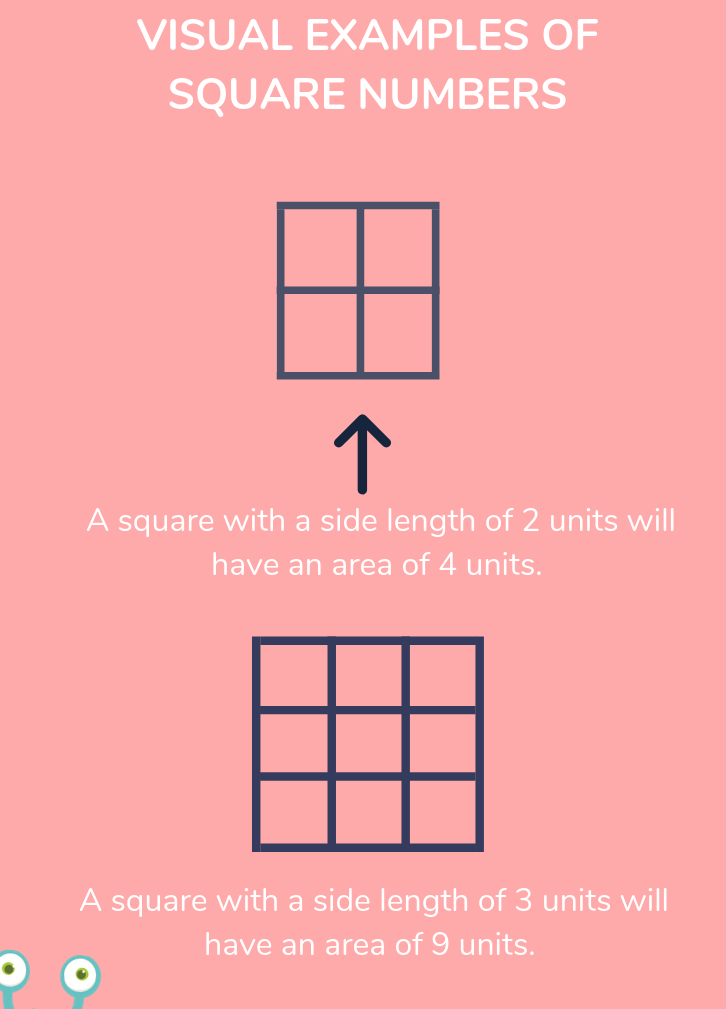Topic exponent and square root worksheet: Unlock the secrets of exponents and square roots with our comprehensive worksheet! Designed to make learning engaging and effective, this worksheet offers a variety of problems to enhance your understanding and boost your confidence in math. Perfect for students and math enthusiasts looking to master these essential concepts.
Table of Content
- Exponent and Square Root Worksheet
- Introduction to Exponents and Square Roots
- Basic Properties of Exponents
- Basic Properties of Square Roots
- Exponent Rules and Laws
- Square Root Rules and Simplification
- Understanding and Solving Exponential Equations
- Solving Square Root Equations
- Mixed Exponent and Square Root Problems
- Practice Problems with Exponents
- Practice Problems with Square Roots
- Real-Life Applications of Exponents
- Real-Life Applications of Square Roots
- Common Mistakes and How to Avoid Them
- Answer Key for Practice Problems
- Additional Resources and Further Reading
- YOUTUBE: Video giải thích khái niệm số mũ và căn bậc hai, giúp học sinh hiểu rõ hơn về các phép toán cơ bản này. Phù hợp cho việc học tập và ôn luyện.
Exponent and Square Root Worksheet
This worksheet will help you practice problems involving exponents and square roots. Below you will find a variety of problems designed to test your understanding of these mathematical concepts. Work through each problem carefully and check your answers.
Exponents
Remember, an exponent indicates how many times a number, called the base, is multiplied by itself. For example, \(2^3 = 2 \times 2 \times 2 = 8\).
- Calculate \(3^4\).
- Evaluate \(2^6\).
- Simplify \(5^3\).
- Find the value of \(4^2\).
- What is \(7^2\)?
Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, \(\sqrt{16} = 4\) because \(4 \times 4 = 16\).
- Calculate \(\sqrt{25}\).
- Evaluate \(\sqrt{49}\).
- Simplify \(\sqrt{64}\).
- Find the value of \(\sqrt{81}\).
- What is \(\sqrt{100}\)?
Mixed Problems
These problems involve both exponents and square roots.
- Simplify \(\sqrt{9} + 2^3\).
- Calculate \(5^2 - \sqrt{36}\).
- Evaluate \((\sqrt{16})^2\).
- Find the value of \(3^3 + \sqrt{49}\).
- Simplify \(4^2 - \sqrt{64}\).
Answers
Check your work against the answers below.
| 1. \(3^4\) | 81 |
| 2. \(2^6\) | 64 |
| 3. \(5^3\) | 125 |
| 4. \(4^2\) | 16 |
| 5. \(7^2\) | 49 |
| 1. \(\sqrt{25}\) | 5 |
| 2. \(\sqrt{49}\) | 7 |
| 3. \(\sqrt{64}\) | 8 |
| 4. \(\sqrt{81}\) | 9 |
| 5. \(\sqrt{100}\) | 10 |
| 1. \(\sqrt{9} + 2^3\) | 11 |
| 2. \(5^2 - \sqrt{36}\) | 19 |
| 3. \((\sqrt{16})^2\) | 16 |
| 4. \(3^3 + \sqrt{49}\) | 34 |
| 5. \(4^2 - \sqrt{64}\) | 0 |

READ MORE:
Introduction to Exponents and Square Roots
Exponents and square roots are fundamental concepts in mathematics that play a crucial role in various applications. Understanding these concepts is essential for solving a wide range of mathematical problems. In this section, we will introduce you to the basics of exponents and square roots, providing you with the foundational knowledge needed to tackle more complex problems.
Exponents
An exponent indicates how many times a number, known as the base, is multiplied by itself. The exponent is written as a small number to the upper right of the base. For example:
- \(2^3 = 2 \times 2 \times 2 = 8\)
- \(5^2 = 5 \times 5 = 25\)
Exponents follow specific rules that make calculations easier. Here are some key rules:
- Product of Powers Rule: \(a^m \times a^n = a^{m+n}\)
- Quotient of Powers Rule: \(\frac{a^m}{a^n} = a^{m-n}\)
- Power of a Power Rule: \((a^m)^n = a^{m \times n}\)
- Zero Exponent Rule: \(a^0 = 1\) (where \(a \neq 0\))
- Negative Exponent Rule: \(a^{-n} = \frac{1}{a^n}\)
Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is the inverse operation of squaring a number. The square root symbol is \(\sqrt{}\). For example:
- \(\sqrt{16} = 4\) because \(4 \times 4 = 16\)
- \(\sqrt{25} = 5\) because \(5 \times 5 = 25\)
Here are some important properties of square roots:
- Product Property: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Square of a Square Root: \((\sqrt{a})^2 = a\)
With these basic principles, you are now equipped to delve deeper into the world of exponents and square roots. Practice regularly to strengthen your understanding and master these essential mathematical tools.
Basic Properties of Exponents
Exponents are a powerful tool in mathematics, allowing us to simplify complex expressions and solve equations more easily. The following properties of exponents are fundamental for working with exponential expressions. By understanding and applying these properties, you can handle a wide variety of mathematical problems with confidence.
Product of Powers Property
When multiplying two expressions that have the same base, you can add the exponents:
\(a^m \times a^n = a^{m+n}\)
For example:
- \(2^3 \times 2^4 = 2^{3+4} = 2^7 = 128\)
- \(5^2 \times 5^3 = 5^{2+3} = 5^5 = 3125\)
Quotient of Powers Property
When dividing two expressions that have the same base, you can subtract the exponents:
\(\frac{a^m}{a^n} = a^{m-n}\)
For example:
- \(\frac{7^5}{7^2} = 7^{5-2} = 7^3 = 343\)
- \(\frac{10^6}{10^4} = 10^{6-4} = 10^2 = 100\)
Power of a Power Property
When raising a power to another power, you can multiply the exponents:
\((a^m)^n = a^{m \times n}\)
For example:
- \((3^2)^4 = 3^{2 \times 4} = 3^8 = 6561\)
- \((6^3)^2 = 6^{3 \times 2} = 6^6 = 46656\)
Power of a Product Property
When raising a product to a power, you can apply the exponent to each factor in the product:
\((ab)^n = a^n \times b^n\)
For example:
- \((2 \times 5)^3 = 2^3 \times 5^3 = 8 \times 125 = 1000\)
- \((3 \times 4)^2 = 3^2 \times 4^2 = 9 \times 16 = 144\)
Power of a Quotient Property
When raising a quotient to a power, you can apply the exponent to both the numerator and the denominator:
\(\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}\)
For example:
- \(\left(\frac{4}{2}\right)^3 = \frac{4^3}{2^3} = \frac{64}{8} = 8\)
- \(\left(\frac{5}{3}\right)^2 = \frac{5^2}{3^2} = \frac{25}{9}\)
Zero Exponent Property
Any non-zero base raised to the zero power is equal to one:
\(a^0 = 1\) (where \(a \neq 0\))
For example:
- \(7^0 = 1\)
- \(100^0 = 1\)
Negative Exponent Property
A negative exponent indicates the reciprocal of the base raised to the corresponding positive exponent:
\(a^{-n} = \frac{1}{a^n}\)
For example:
- \(2^{-3} = \frac{1}{2^3} = \frac{1}{8}\)
- \(5^{-2} = \frac{1}{5^2} = \frac{1}{25}\)
By mastering these basic properties of exponents, you can simplify and solve exponential expressions with ease. Practice these properties regularly to enhance your mathematical skills and confidence.
Basic Properties of Square Roots
Square roots are essential in mathematics, providing a way to reverse the process of squaring a number. Understanding the basic properties of square roots will help you simplify and solve a variety of mathematical problems. This section covers the fundamental properties and rules of square roots.
Definition of Square Root
The square root of a number \(a\) is a value that, when multiplied by itself, gives \(a\). It is denoted by the symbol \(\sqrt{a}\). For example:
- \(\sqrt{16} = 4\) because \(4 \times 4 = 16\)
- \(\sqrt{25} = 5\) because \(5 \times 5 = 25\)
Product Property of Square Roots
The square root of a product is equal to the product of the square roots of the factors:
\(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
For example:
- \(\sqrt{4 \times 9} = \sqrt{36} = 6\) and \(\sqrt{4} \times \sqrt{9} = 2 \times 3 = 6\)
- \(\sqrt{2 \times 8} = \sqrt{16} = 4\) and \(\sqrt{2} \times \sqrt{8} = \sqrt{16} = 4\)
Quotient Property of Square Roots
The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
For example:
- \(\sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}} = \frac{5}{3}\)
- \(\sqrt{\frac{16}{4}} = \frac{\sqrt{16}}{\sqrt{4}} = \frac{4}{2} = 2\)
Square of a Square Root
The square of a square root returns the original number:
\((\sqrt{a})^2 = a\)
For example:
- \((\sqrt{5})^2 = 5\)
- \((\sqrt{10})^2 = 10\)
Square Root of a Square
The square root of a squared number returns the absolute value of the original number:
\(\sqrt{a^2} = |a|\)
For example:
- \(\sqrt{(-4)^2} = \sqrt{16} = 4\)
- \(\sqrt{6^2} = \sqrt{36} = 6\)
Simplifying Square Roots
Square roots can often be simplified by factoring out perfect squares:
- \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)
- \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\)
By understanding these basic properties, you can simplify and solve square root expressions with greater ease and confidence. Practice applying these properties to various problems to enhance your skills in working with square roots.
Exponent Rules and Laws
Understanding the rules and laws of exponents is crucial for simplifying expressions and solving equations involving exponents. These rules make it easier to work with large numbers and complex calculations. Here, we will explore the key exponent rules and laws step by step.
Product of Powers Rule
When multiplying two expressions with the same base, add the exponents:
\(a^m \times a^n = a^{m+n}\)
For example:
- \(2^3 \times 2^4 = 2^{3+4} = 2^7 = 128\)
- \(5^2 \times 5^3 = 5^{2+3} = 5^5 = 3125\)
Quotient of Powers Rule
When dividing two expressions with the same base, subtract the exponents:
\(\frac{a^m}{a^n} = a^{m-n}\)
For example:
- \(\frac{7^5}{7^2} = 7^{5-2} = 7^3 = 343\)
- \(\frac{10^6}{10^4} = 10^{6-4} = 10^2 = 100\)
Power of a Power Rule
When raising a power to another power, multiply the exponents:
\((a^m)^n = a^{m \times n}\)
For example:
- \((3^2)^4 = 3^{2 \times 4} = 3^8 = 6561\)
- \((6^3)^2 = 6^{3 \times 2} = 6^6 = 46656\)
Power of a Product Rule
When raising a product to a power, apply the exponent to each factor in the product:
\((ab)^n = a^n \times b^n\)
For example:
- \((2 \times 5)^3 = 2^3 \times 5^3 = 8 \times 125 = 1000\)
- \((3 \times 4)^2 = 3^2 \times 4^2 = 9 \times 16 = 144\)
Power of a Quotient Rule
When raising a quotient to a power, apply the exponent to both the numerator and the denominator:
\(\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}\)
For example:
- \(\left(\frac{4}{2}\right)^3 = \frac{4^3}{2^3} = \frac{64}{8} = 8\)
- \(\left(\frac{5}{3}\right)^2 = \frac{5^2}{3^2} = \frac{25}{9}\)
Zero Exponent Rule
Any non-zero base raised to the zero power is equal to one:
\(a^0 = 1\) (where \(a \neq 0\))
For example:
- \(7^0 = 1\)
- \(100^0 = 1\)
Negative Exponent Rule
A negative exponent indicates the reciprocal of the base raised to the corresponding positive exponent:
\(a^{-n} = \frac{1}{a^n}\)
For example:
- \(2^{-3} = \frac{1}{2^3} = \frac{1}{8}\)
- \(5^{-2} = \frac{1}{5^2} = \frac{1}{25}\)
These exponent rules and laws are fundamental for simplifying and solving exponential expressions. By mastering these principles, you can efficiently handle complex mathematical problems involving exponents.

Square Root Rules and Simplification
Square roots are an essential part of mathematics, and understanding how to simplify them is crucial for solving various mathematical problems. This section covers the rules of square roots and the steps to simplify them effectively.
Basic Square Root Rules
Several fundamental rules govern the operations involving square roots:
- Product Property: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Square of a Square Root: \((\sqrt{a})^2 = a\)
These rules allow you to break down and manipulate square roots more easily, making complex expressions simpler to handle.
Simplifying Square Roots
To simplify square roots, follow these steps:
- Factor the Number: Break down the number under the square root into its prime factors or into factors where one is a perfect square.
- Apply the Product Property: Use the product property to separate the square root into simpler parts.
- Simplify: Take the square root of any perfect squares.
Here are some examples:
- Example 1: Simplify \(\sqrt{50}\)
- Factor the number: \(50 = 25 \times 2\)
- Apply the product property: \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2}\)
- Simplify: \(\sqrt{25} = 5\), so \(\sqrt{50} = 5\sqrt{2}\)
- Example 2: Simplify \(\sqrt{72}\)
- Factor the number: \(72 = 36 \times 2\)
- Apply the product property: \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2}\)
- Simplify: \(\sqrt{36} = 6\), so \(\sqrt{72} = 6\sqrt{2}\)
Combining Square Roots
Sometimes, you will need to add or subtract square roots. This can only be done when the square roots have the same radicand (the number under the square root). For example:
- \(2\sqrt{3} + 3\sqrt{3} = (2 + 3)\sqrt{3} = 5\sqrt{3}\)
- \(5\sqrt{2} - 2\sqrt{2} = (5 - 2)\sqrt{2} = 3\sqrt{2}\)
If the radicands are different, you cannot combine the square roots directly. Instead, look for ways to simplify each square root first.
Rationalizing the Denominator
Rationalizing the denominator involves eliminating any square roots from the denominator of a fraction. To do this, multiply the numerator and the denominator by the square root present in the denominator. For example:
- \(\frac{3}{\sqrt{5}}\)
- Multiply by \(\frac{\sqrt{5}}{\sqrt{5}}\): \(\frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5}\)
- \(\frac{7}{\sqrt{2}}\)
- Multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\): \(\frac{7}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{7\sqrt{2}}{2}\)
By mastering these rules and simplification techniques, you can handle square roots confidently and effectively in various mathematical problems.
Understanding and Solving Exponential Equations
Exponential equations involve variables in the exponent and are common in various fields such as science, engineering, and finance. Solving these equations requires understanding their properties and applying specific techniques. This section will guide you through understanding and solving exponential equations step by step.
Basic Form of Exponential Equations
An exponential equation can generally be written in the form:
\(a \cdot b^{cx} = d\)
where \(a\), \(b\), \(c\), and \(d\) are constants, and \(x\) is the variable to be solved.
Solving Simple Exponential Equations
For equations where both sides can be written with the same base, follow these steps:
- Rewrite both sides with the same base: If possible, express both sides of the equation as powers of the same base.
- Set the exponents equal: Once the bases are the same, set the exponents equal to each other.
- Solve for the variable: Solve the resulting equation for the variable.
For example:
- \(2^{3x} = 8\)
- Rewrite \(8\) as \(2^3\): \(2^{3x} = 2^3\)
- Set the exponents equal: \(3x = 3\)
- Solve for \(x\): \(x = 1\)
Using Logarithms to Solve Exponential Equations
When the equation cannot be rewritten with the same base, use logarithms:
- Take the logarithm of both sides: Use a logarithm to bring the exponent down as a coefficient. Common logarithms (base 10) or natural logarithms (base \(e\)) are usually used.
- Apply the logarithm rule: Use the property \(\log_b(a^c) = c \cdot \log_b(a)\) to simplify.
- Solve for the variable: Isolate the variable and solve.
For example:
- \(5^{2x} = 20\)
- Take the natural logarithm of both sides: \(\ln(5^{2x}) = \ln(20)\)
- Apply the logarithm rule: \(2x \cdot \ln(5) = \ln(20)\)
- Solve for \(x\): \(x = \frac{\ln(20)}{2 \cdot \ln(5)}\)
- Use a calculator to find the value: \(x \approx 0.862\)
Exponential Equations with Different Bases
For equations with different bases, logarithms are also useful:
- \(3^{x+1} = 4^{2x}\)
- Take the natural logarithm of both sides: \(\ln(3^{x+1}) = \ln(4^{2x})\)
- Apply the logarithm rule: \((x+1) \cdot \ln(3) = 2x \cdot \ln(4)\)
- Distribute and solve for \(x\):
- \(x \cdot \ln(3) + \ln(3) = 2x \cdot \ln(4)\)
- \(\ln(3) = 2x \cdot \ln(4) - x \cdot \ln(3)\)
- \(\ln(3) = x (2 \ln(4) - \ln(3))\)
- \(x = \frac{\ln(3)}{2 \ln(4) - \ln(3)}\)
- Use a calculator to find the value: \(x \approx 0.385\)
By mastering these methods, you can solve a wide range of exponential equations effectively. Practice with different problems to enhance your skills and confidence in dealing with exponential equations.
Solving Square Root Equations
Square root equations are equations in which the variable is under a square root. Solving these equations involves isolating the square root and then squaring both sides to eliminate the square root. Below, we will explore the detailed steps to solve square root equations effectively.
Steps to Solve Square Root Equations
Follow these steps to solve square root equations:
- Isolate the Square Root: Move terms so that the square root is by itself on one side of the equation.
- Square Both Sides: Eliminate the square root by squaring both sides of the equation.
- Solve the Resulting Equation: Solve the equation obtained after squaring for the variable.
- Check for Extraneous Solutions: Substitute the solutions back into the original equation to verify, as squaring can introduce extraneous solutions.
Example 1: Solving a Simple Square Root Equation
Consider the equation: \(\sqrt{x} = 3\)
- Isolate the Square Root: The square root is already isolated.
- Square Both Sides: \((\sqrt{x})^2 = 3^2\)
- Solve for \(x\): \(x = 9\)
- Check the Solution: \(\sqrt{9} = 3\), which is true. Thus, \(x = 9\) is a valid solution.
Example 2: Solving a Square Root Equation with Additional Terms
Consider the equation: \(\sqrt{x + 4} = x - 2\)
- Isolate the Square Root: The square root is already isolated.
- Square Both Sides: \((\sqrt{x + 4})^2 = (x - 2)^2\)
- Solve for \(x\):
- \(x + 4 = x^2 - 4x + 4\)
- Rearrange the equation: \(0 = x^2 - 5x\)
- Factor the equation: \(0 = x(x - 5)\)
- Find the solutions: \(x = 0\) or \(x = 5\)
- Check for Extraneous Solutions:
- For \(x = 0\): \(\sqrt{0 + 4} = 0 - 2\), which simplifies to \(2 \neq -2\). So, \(x = 0\) is extraneous.
- For \(x = 5\): \(\sqrt{5 + 4} = 5 - 2\), which simplifies to \(3 = 3\). So, \(x = 5\) is valid.
The valid solution is \(x = 5\).
Example 3: Solving a Square Root Equation with Two Square Roots
Consider the equation: \(\sqrt{2x + 3} = \sqrt{x + 9}\)
- Isolate the Square Roots: The square roots are already isolated.
- Square Both Sides: \((\sqrt{2x + 3})^2 = (\sqrt{x + 9})^2\)
- Solve for \(x\):
- \(2x + 3 = x + 9\)
- Rearrange the equation: \(x = 6\)
- Check for Extraneous Solutions:
- For \(x = 6\): \(\sqrt{2(6) + 3} = \sqrt{6 + 9}\), which simplifies to \(\sqrt{15} = \sqrt{15}\). So, \(x = 6\) is valid.
The valid solution is \(x = 6\).
By following these steps, you can effectively solve square root equations and ensure that you find the correct solutions while avoiding extraneous ones.
Mixed Exponent and Square Root Problems
In this section, we will tackle problems that combine the use of both exponents and square roots. These problems require understanding the properties and rules of both mathematical operations. Below are some example problems and solutions to help you master these concepts.
Example Problems
-
Problem: Simplify \( \sqrt{16} \times 2^3 \)
Solution:
\( \sqrt{16} = 4 \) and \( 2^3 = 8 \), so \( \sqrt{16} \times 2^3 = 4 \times 8 = 32 \)
-
Problem: Simplify \( \sqrt{25} \times 3^2 \)
Solution:
\( \sqrt{25} = 5 \) and \( 3^2 = 9 \), so \( \sqrt{25} \times 3^2 = 5 \times 9 = 45 \)
-
Problem: Simplify \( \left(\sqrt{9}\right)^3 \)
Solution:
\( \sqrt{9} = 3 \), so \( \left(\sqrt{9}\right)^3 = 3^3 = 27 \)
-
Problem: Simplify \( \sqrt{36} \times 4^2 \)
Solution:
\( \sqrt{36} = 6 \) and \( 4^2 = 16 \), so \( \sqrt{36} \times 4^2 = 6 \times 16 = 96 \)
-
Problem: Simplify \( \left(\sqrt{49}\right)^2 \)
Solution:
\( \sqrt{49} = 7 \), so \( \left(\sqrt{49}\right)^2 = 7^2 = 49 \)
Practice Problems
Try to solve the following problems on your own. Check your answers with the solutions provided below.
-
Simplify \( \sqrt{64} \times 5^2 \)
-
Simplify \( \left(\sqrt{81}\right)^2 \)
-
Simplify \( \sqrt{100} \times 3^3 \)
-
Simplify \( \left(\sqrt{144}\right)^2 \)
-
Simplify \( \sqrt{121} \times 2^4 \)
Solutions to Practice Problems
-
\( \sqrt{64} = 8 \) and \( 5^2 = 25 \), so \( \sqrt{64} \times 5^2 = 8 \times 25 = 200 \)
-
\( \sqrt{81} = 9 \), so \( \left(\sqrt{81}\right)^2 = 9^2 = 81 \)
-
\( \sqrt{100} = 10 \) and \( 3^3 = 27 \), so \( \sqrt{100} \times 3^3 = 10 \times 27 = 270 \)
-
\( \sqrt{144} = 12 \), so \( \left(\sqrt{144}\right)^2 = 12^2 = 144 \)
-
\( \sqrt{121} = 11 \) and \( 2^4 = 16 \), so \( \sqrt{121} \times 2^4 = 11 \times 16 = 176 \)
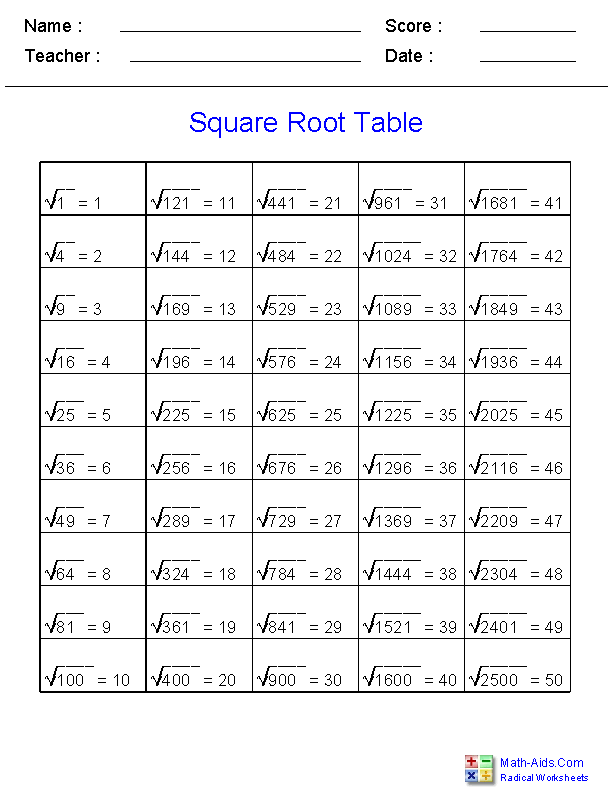
Practice Problems with Exponents
Practice problems are a great way to solidify your understanding of exponents. Below, you will find a variety of problems ranging from basic to more advanced levels. Try solving each problem step-by-step, and refer to the solutions provided to check your work.
Basic Problems
- Simplify the expression: \( 2^3 \)
- Calculate \( 5^2 \)
- Evaluate \( 3^4 \)
- Find the value of \( 7^0 \)
- Simplify \( 10^3 \times 10^2 \)
Intermediate Problems
- Simplify the expression: \( (2^3)^2 \)
- Calculate \( 4^2 \times 4^3 \)
- Evaluate \( \frac{6^5}{6^2} \)
- Simplify \( 9^{-2} \)
- Find the value of \( (3^2 \times 3^4) \div 3^3 \)
Advanced Problems
- Simplify the expression: \( (2^3 \times 5^2)^2 \)
- Calculate \( \left(\frac{4^3}{2^3}\right)^2 \)
- Evaluate \( (10^{-1})^3 \)
- Simplify \( \frac{2^4 \times 3^3}{6^2} \)
- Find the value of \( (2^3 \times 3^2)^{-1} \)
Solutions
| Problem | Solution |
|---|---|
| Simplify the expression: \( 2^3 \) | \( 2^3 = 8 \) |
| Calculate \( 5^2 \) | \( 5^2 = 25 \) |
| Evaluate \( 3^4 \) | \( 3^4 = 81 \) |
| Find the value of \( 7^0 \) | \( 7^0 = 1 \) |
| Simplify \( 10^3 \times 10^2 \) | \( 10^3 \times 10^2 = 10^{3+2} = 10^5 = 100,000 \) |
| Simplify the expression: \( (2^3)^2 \) | \( (2^3)^2 = 2^{3 \times 2} = 2^6 = 64 \) |
| Calculate \( 4^2 \times 4^3 \) | \( 4^2 \times 4^3 = 4^{2+3} = 4^5 = 1024 \) |
| Evaluate \( \frac{6^5}{6^2} \) | \( \frac{6^5}{6^2} = 6^{5-2} = 6^3 = 216 \) |
| Simplify \( 9^{-2} \) | \( 9^{-2} = \frac{1}{9^2} = \frac{1}{81} \) |
| Find the value of \( (3^2 \times 3^4) \div 3^3 \) | \( (3^2 \times 3^4) \div 3^3 = 3^{2+4-3} = 3^3 = 27 \) |
| Simplify the expression: \( (2^3 \times 5^2)^2 \) | \( (2^3 \times 5^2)^2 = 2^{3 \times 2} \times 5^{2 \times 2} = 2^6 \times 5^4 = 64 \times 625 = 40,000 \) |
| Calculate \( \left(\frac{4^3}{2^3}\right)^2 \) | \( \left(\frac{4^3}{2^3}\right)^2 = \left(\frac{(2^2)^3}{2^3}\right)^2 = \left(\frac{2^6}{2^3}\right)^2 = (2^3)^2 = 2^6 = 64 \) |
| Evaluate \( (10^{-1})^3 \) | \( (10^{-1})^3 = 10^{-3} = \frac{1}{10^3} = \frac{1}{1000} = 0.001 \) |
| Simplify \( \frac{2^4 \times 3^3}{6^2} \) | \( \frac{2^4 \times 3^3}{6^2} = \frac{2^4 \times 3^3}{(2 \times 3)^2} = \frac{2^4 \times 3^3}{2^2 \times 3^2} = 2^{4-2} \times 3^{3-2} = 2^2 \times 3^1 = 4 \times 3 = 12 \) |
| Find the value of \( (2^3 \times 3^2)^{-1} \) | \( (2^3 \times 3^2)^{-1} = \frac{1}{2^3 \times 3^2} = \frac{1}{8 \times 9} = \frac{1}{72} \) |
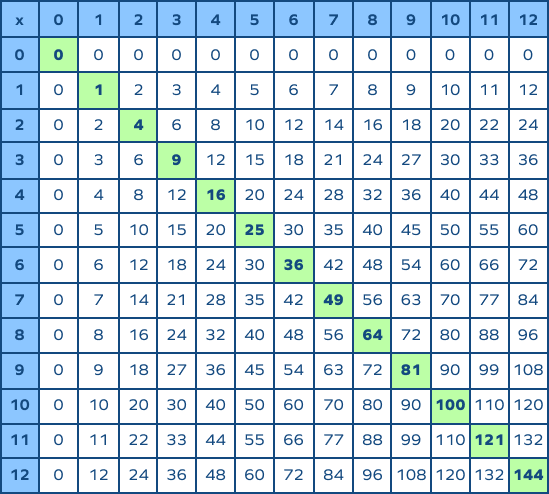
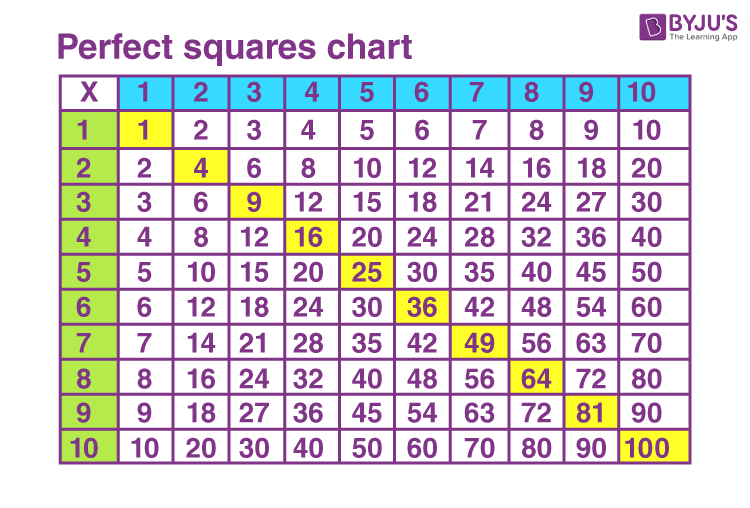
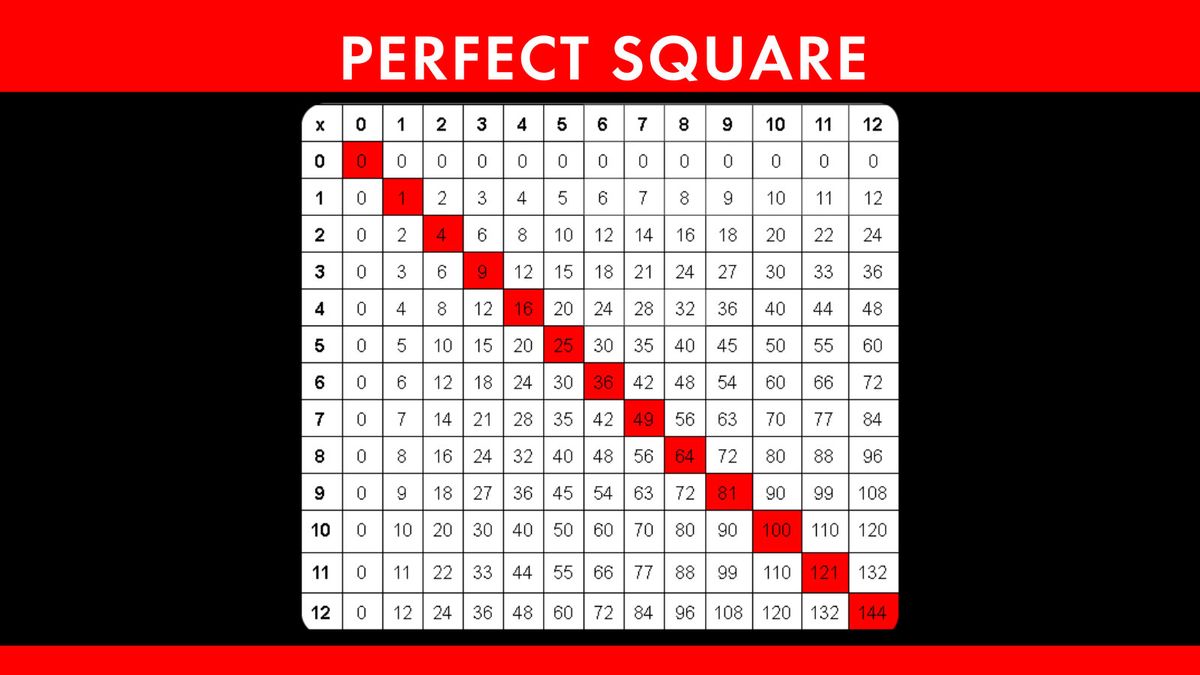
Practice Problems with Square Roots
Here are a series of practice problems designed to help you master the concept of square roots. Follow the steps provided to solve each problem. Remember, the square root of a number is a value that, when multiplied by itself, gives the original number.
-
Find the square roots of perfect squares:
- What is the square root of 49?
- What is the square root of 144?
- What is the square root of 256?
- What is the square root of 625?
- What is the square root of 1024?
Steps:
- Identify if the number is a perfect square.
- Determine the number that, when multiplied by itself, results in the given number.
-
Estimate the square roots of non-perfect squares:
- Estimate the square root of 50.
- Estimate the square root of 200.
- Estimate the square root of 500.
- Estimate the square root of 800.
- Estimate the square root of 1000.
Steps:
- Find the two closest perfect squares between which the number lies.
- Use these values to estimate the square root.
-
Simplify square roots:
- Simplify √18.
- Simplify √50.
- Simplify √72.
- Simplify √98.
- Simplify √128.
Steps:
- Factor the number into its prime factors.
- Pair the prime factors and move them outside the square root symbol.
- Multiply the numbers outside the square root.
- Leave the unpaired factors inside the square root.
For each problem, write your answers and check your work. Practice consistently to build your confidence and understanding of square roots.
Real-Life Applications of Exponents
Exponents are widely used in various real-life scenarios. Understanding these applications can help in comprehending the importance and practical usage of exponents.
1. Population Growth
Population growth is often modeled using exponential functions. For example, if a population of a town grows at an annual rate of 2%, the population after \( n \) years can be represented as:
\[ P = P_0 \times (1 + r)^n \]
where:
- \( P \) is the future population
- \( P_0 \) is the current population
- \( r \) is the growth rate (in decimal form)
- \( n \) is the number of years
2. Compound Interest
Compound interest is another area where exponents are crucial. The formula to calculate compound interest is:
\[ A = P \left(1 + \frac{r}{n}\right)^{nt} \]
where:
- \( A \) is the amount of money accumulated after \( n \) years, including interest.
- \( P \) is the principal amount (the initial amount of money).
- \( r \) is the annual interest rate (decimal).
- \( n \) is the number of times interest is compounded per year.
- \( t \) is the time the money is invested or borrowed for, in years.
3. Radioactive Decay
Radioactive materials decay at a rate proportional to their current amount, which can be modeled using exponents. The formula is:
\[ N(t) = N_0 e^{-\lambda t} \]
where:
- \( N(t) \) is the quantity that still remains after time \( t \).
- \( N_0 \) is the initial quantity.
- \( \lambda \) is the decay constant.
- \( t \) is the time elapsed.
4. Bacterial Growth
Bacteria multiply rapidly, and their growth can be described using exponential functions. The number of bacteria \( N \) at time \( t \) can be modeled as:
\[ N(t) = N_0 e^{kt} \]
where:
- \( N(t) \) is the number of bacteria at time \( t \).
- \( N_0 \) is the initial number of bacteria.
- \( k \) is the growth rate constant.
- \( t \) is the time elapsed.
5. Earthquake Intensity
The Richter scale for measuring the magnitude of earthquakes is logarithmic, meaning each whole number increase on the scale represents a tenfold increase in measured amplitude and roughly 31.6 times more energy release. The magnitude \( M \) is calculated as:
\[ M = \log_{10}\left(\frac{A}{A_0}\right) \]
where:
- \( A \) is the amplitude of seismic waves.
- \( A_0 \) is a reference amplitude.
Real-Life Applications of Square Roots
Square roots are used in various real-life situations and fields. Here are some practical applications where square roots play a crucial role:
- Geometry and Construction
In geometry, square roots are used to find the lengths of the sides of squares and right triangles. For example, using the Pythagorean theorem, the length of the hypotenuse of a right triangle can be found if the lengths of the other two sides are known:
\[ c = \sqrt{a^2 + b^2} \]
where \( c \) is the hypotenuse, and \( a \) and \( b \) are the other two sides of the triangle.
- Physics
Square roots are used in physics to calculate various properties such as energy, force, and velocity. For instance, the formula to find the velocity \( v \) of an object in free fall (ignoring air resistance) after time \( t \) is:
\[ v = \sqrt{2gh} \]
where \( g \) is the acceleration due to gravity, and \( h \) is the height.
- Finance
In finance, square roots are used to calculate the volatility of stock prices and the standard deviation of investment returns. For example, the standard deviation \( \sigma \) is given by:
\[ \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2} \]
where \( N \) is the number of observations, \( x_i \) are the individual observations, and \( \mu \) is the mean.
- Engineering
In engineering, square roots are used in various calculations, including stress analysis and signal processing. For example, the RMS (Root Mean Square) value of an alternating current (AC) signal is calculated using:
\[ \text{RMS} = \sqrt{\frac{1}{T} \int_0^T [f(t)]^2 \, dt} \]
where \( T \) is the period of the signal, and \( f(t) \) is the function representing the signal.
Understanding and applying square roots can simplify many calculations and help solve real-world problems efficiently.

Common Mistakes and How to Avoid Them
Understanding and avoiding common mistakes in working with exponents and square roots is crucial for mastering these concepts. Below are some frequent errors and tips on how to prevent them.
Mistakes with Exponents
- Incorrectly Adding Exponents:
When multiplying two exponential terms with the same base, students often multiply the exponents instead of adding them.
Mistake: \(a^m \times a^n = a^{m \times n}\)
Correct: \(a^m \times a^n = a^{m+n}\)
To avoid this mistake, remember the product rule: add the exponents when the bases are the same.
- Misapplying the Power Rule:
When raising a power to another power, students sometimes add the exponents instead of multiplying them.
Mistake: \((a^m)^n = a^{m+n}\)
Correct: \((a^m)^n = a^{m \times n}\)
Use the power rule correctly by multiplying the exponents.
- Negative Exponents:
Misunderstanding negative exponents can lead to errors. A negative exponent indicates a reciprocal.
Mistake: \(a^{-n} = -a^n\)
Correct: \(a^{-n} = \frac{1}{a^n}\)
Remember, a negative exponent means taking the reciprocal of the base raised to the positive exponent.
Mistakes with Square Roots
- Ignoring Both Positive and Negative Roots:
When solving equations like \(x^2 = 9\), students often only consider the positive root.
Mistake: \(x^2 = 9 \Rightarrow x = 3\)
Correct: \(x^2 = 9 \Rightarrow x = \pm 3\)
Always include both the positive and negative solutions when taking the square root of both sides of an equation.
- Misinterpreting the Square Root Symbol:
The square root symbol (√) by itself denotes only the principal (non-negative) square root.
Mistake: \(\sqrt{25} = \pm 5\)
Correct: \(\sqrt{25} = 5\)
Use the ± symbol to indicate both roots when solving equations, but remember the square root symbol refers to the principal root.
- Handling Square Roots in Equations:
When squaring both sides of an equation, ensure all possible solutions are checked, including extraneous ones.
Mistake: \(\sqrt{x+3} = 4 \Rightarrow x + 3 = 16\)
Correct: \(\sqrt{x+3} = 4 \Rightarrow x + 3 = 16 \Rightarrow x = 13\) (Check if the solution is valid in the original equation)
Verify solutions by substituting them back into the original equation to ensure they satisfy it.
By being aware of these common mistakes and understanding the correct approaches, you can improve your accuracy and confidence in working with exponents and square roots.
Answer Key for Practice Problems
Below are the answers for the practice problems on exponents and square roots. Ensure to review your solutions and understand any mistakes made.
Answers for Exponent Problems
- \(2^3 = 8\)
- \(5^2 = 25\)
- \(3^4 = 81\)
- \(10^3 = 1000\)
- \(4^2 = 16\)
- \(6^2 = 36\)
- \(2^5 = 32\)
- \(7^3 = 343\)
- \(8^2 = 64\)
- \(9^2 = 81\)
Answers for Square Root Problems
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
- \(\sqrt{36} = 6\)
- \(\sqrt{49} = 7\)
- \(\sqrt{64} = 8\)
- \(\sqrt{81} = 9\)
- \(\sqrt{100} = 10\)
- \(\sqrt{121} = 11\)
Mixed Exponent and Square Root Problems
- \(2^3 + \sqrt{16} = 8 + 4 = 12\)
- \(3^2 - \sqrt{9} = 9 - 3 = 6\)
- \(4^2 + \sqrt{25} = 16 + 5 = 21\)
- \(5^3 - \sqrt{36} = 125 - 6 = 119\)
- \(2^4 + \sqrt{49} = 16 + 7 = 23\)
If you have any questions about the solutions or need further clarification, please review the relevant sections in your study materials or reach out to your instructor.
Additional Resources and Further Reading
Here are some valuable resources for further reading and practice on exponents and square roots:
-
Khan Academy - Exponents and Radicals
This comprehensive resource provides detailed lessons, practice exercises, and quizzes on exponents and radicals, including higher-order roots.
-
Math-Aids.com - Exponents Worksheets
A collection of printable worksheets that cover various topics on exponents, including properties, operations, and real-life applications.
-
K5 Learning - Exponents Worksheets
Offers a range of free, printable worksheets focused on exponent notation, expressions, and practice problems for different grade levels.
-
IXL Learning - Exponent Practice
Interactive practice problems and activities designed to help students master exponent rules and applications.
-
Coolmath - Exponents and Radicals
Explanations and examples to help students understand and practice exponent and radical concepts.
These resources will provide additional explanations, examples, and practice problems to further enhance your understanding and skills in working with exponents and square roots.
Video giải thích khái niệm số mũ và căn bậc hai, giúp học sinh hiểu rõ hơn về các phép toán cơ bản này. Phù hợp cho việc học tập và ôn luyện.
Math Antics - Số Mũ và Căn Bậc Hai
READ MORE:
Video giải thích khái niệm căn bậc hai, cung cấp các ví dụ minh họa và phương pháp tính toán, phù hợp cho học sinh học tập và ôn luyện.
Căn Bậc Hai Là Gì? | Toán Học với Thầy J