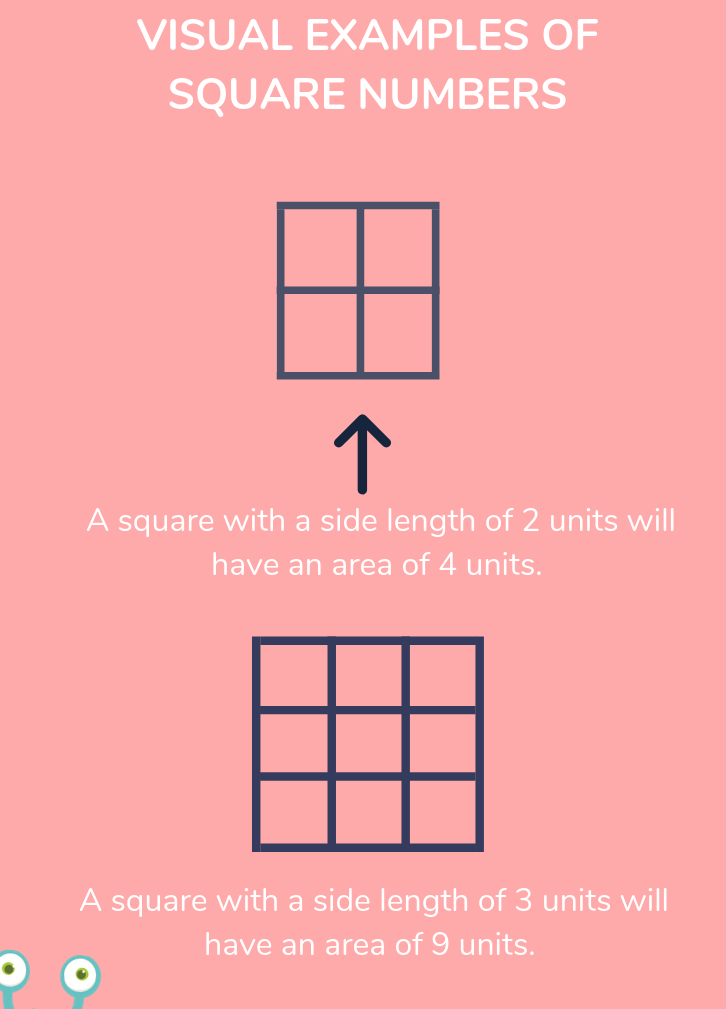Topic square root worksheet answers: Discover comprehensive square root worksheet answers to enhance your math skills. This article provides detailed solutions and explanations for various square root problems, helping students and educators alike. Dive into practice exercises, understand perfect squares, and simplify square roots with ease. Explore now to master your math abilities efficiently.
Table of Content
- Square Root Worksheet Answers
- Introduction to Square Roots
- Basic Concepts and Definitions
- Finding Square Roots Manually
- Square Root Properties
- Simplifying Square Roots
- Square Roots of Fractions
- Square Roots of Decimals
- Perfect Squares
- Square Root Calculation Methods
- Worksheets and Practice Problems
- Square Root Quiz and Review
- Answer Keys and Explanations
- Advanced Square Root Applications
- Related Mathematical Concepts
- Additional Resources and References
- YOUTUBE: Xem video Bình phương căn và căn bậc ba để học cách giải các bài tập về bình phương căn và câu hỏi liên quan.
Square Root Worksheet Answers
Understanding square roots is fundamental in various math levels, including pre-algebra and algebra. Below are details on various resources that provide square root worksheets along with answers, ensuring students grasp the concept efficiently.
Key Resources
- Math Worksheets 4 Kids: This site offers printable worksheets focused on perfect squares, reducing non-perfect squares to their simplest radical form, and more. These worksheets are suitable for 6th to 8th-grade students. Some resources are free of charge.
- Easy Teacher Worksheets: Provides step-by-step guides on finding square roots, including practice problems and quizzes. Topics include simplifying square roots with negative numbers and fractional bases.
- Online Math Learning: Features printable worksheets with answers on the second page. Topics include simplifying square roots of whole numbers and fractions, along with related lessons and videos to aid in learning.
- Math-Drills.com: Offers downloadable and printable worksheets that can be used for classroom practice or homeschooling. The worksheets include problems on both perfect squares and simplifying non-perfect squares.
- iMathWorksheets.com: Provides a variety of worksheets for different math topics including square roots. These worksheets cover various difficulty levels and offer step-by-step solutions.
Examples of Worksheet Problems
- Find the square root of the following perfect squares:
- √144
- √784
- √2401
- Simplify the following square roots:
- √50
- √1.9 x 240
- Find the side length of a square with the given area:
- 36 ft2
- 100 cm2
How to Use These Worksheets
Students can practice these worksheets to master the skill of finding and simplifying square roots. Teachers and parents can use them as supplementary materials to enhance learning, provide extra practice, or prepare students for tests. Solutions are often provided, making it easier to check answers and understand any mistakes.
Conclusion
Square root worksheets with answers are valuable tools in both classroom settings and home study environments. By practicing with these resources, students can build a strong foundation in understanding and working with square roots.
| Resource | Description |
|---|---|
| Math Worksheets 4 Kids | Printable worksheets for 6th to 8th-grade students, including perfect squares and radical forms. |
| Easy Teacher Worksheets | Step-by-step guides and practice problems on finding and simplifying square roots. |
| Online Math Learning | Printable worksheets with answers, videos, and related lessons for simplifying square roots. |
| Math-Drills.com | Downloadable worksheets for classroom and homeschooling, covering both perfect and non-perfect squares. |
| iMathWorksheets.com | Various worksheets covering square roots and other math topics, with detailed solutions. |

READ MORE:
Introduction to Square Roots
Understanding square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 25 is 5, because 5 × 5 = 25. This concept is crucial for solving various mathematical problems, from basic equations to more complex algebraic expressions.
To simplify square roots, follow these steps:
- Identify the perfect squares that are factors of the number under the square root.
- Rewrite the square root as the product of the square root of the perfect square and the square root of the remaining factor.
- Simplify the expression by taking the square root of the perfect square.
For example, to simplify √72:
- 72 can be factored into 36 × 2.
- So, √72 = √(36 × 2).
- This can be written as √36 × √2.
- Since √36 is 6, the simplified form is 6√2.
Square roots can also be applied to fractions. To simplify the square root of a fraction:
- Simplify the numerator and the denominator separately.
- If possible, simplify the resulting fraction further.
For example, to simplify √(49/16):
- Take the square root of the numerator and the denominator separately: √49 / √16.
- Since √49 is 7 and √16 is 4, the simplified form is 7/4.
Understanding and practicing these steps will help in mastering the concept of square roots, making it easier to tackle more advanced mathematical challenges.
Basic Concepts and Definitions
Understanding square roots is essential in mathematics. A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). In other words, \( y \) is a value that, when multiplied by itself, gives \( x \). The square root is denoted by the radical symbol \( \sqrt{} \). For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
There are several key concepts and definitions related to square roots:
- Perfect Square: A perfect square is an integer that is the square of another integer. For example, \( 1, 4, 9, 16, \) and \( 25 \) are perfect squares because they can be written as \( 1^2, 2^2, 3^2, 4^2, \) and \( 5^2 \), respectively.
- Principal Square Root: The principal square root is the non-negative square root of a number. For any positive number \( a \), the principal square root is denoted as \( \sqrt{a} \). For example, the principal square root of \( 9 \) is \( 3 \) because \( 3 \) is non-negative and \( 3 \times 3 = 9 \).
- Negative Square Roots: While the principal square root is non-negative, every positive number actually has two square roots: one positive and one negative. For example, \( \sqrt{25} = 5 \) and \( \sqrt{25} = -5 \) because both \( 5 \times 5 = 25 \) and \( -5 \times -5 = 25 \).
- Imaginary Numbers: If a number is negative, its square root is not a real number. Instead, it is an imaginary number. The square root of \( -1 \) is denoted as \( i \), where \( i \) is the imaginary unit. Thus, \( \sqrt{-9} = 3i \) because \( (3i) \times (3i) = 9i^2 = -9 \).
Here is a step-by-step approach to finding the square root of a number:
- Identify if the number is a perfect square. If it is, find the integer that, when squared, equals the original number.
- If the number is not a perfect square, use approximation methods such as the long division method or a calculator for more precision.
- If dealing with a negative number, remember that the result will be an imaginary number involving \( i \).
- For fractions, find the square root of the numerator and the denominator separately. For example, \( \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2} \).
Understanding these basic concepts and definitions will help you work with square roots effectively and solve related mathematical problems.
Finding Square Roots Manually
Finding square roots manually can be done through various methods. Below are the detailed steps to manually find square roots using the prime factorization method and the long division method.
Prime Factorization Method
- First, express the number as a product of its prime factors. For example, for \( \sqrt{36} \):
- 36 can be written as \( 2 \times 2 \times 3 \times 3 \).
- Pair the prime factors:
- \( 36 = (2 \times 2) \times (3 \times 3) \).
- Take one factor from each pair and multiply them together:
- \( 2 \times 3 = 6 \).
- Thus, \( \sqrt{36} = 6 \).
Long Division Method
- Start by grouping the digits in pairs from right to left. For example, to find \( \sqrt{529} \):
- Group as 5 | 29.
- Find the largest number whose square is less than or equal to the first group (5):
- The largest number is 2 because \( 2^2 = 4 \leq 5 \).
- Subtract the square of this number from the first group and bring down the next pair of digits:
- \( 5 - 4 = 1 \), bring down 29 to get 129.
- Double the number from step 2 (2) and write it as a tentative divisor:
- Tentative divisor is 4_.
- Find a digit \( x \) such that \( (40 + x) \times x \leq 129 \):
- \( 43 \times 3 = 129 \).
- Place this digit next to the initial guess and also in the quotient:
- The quotient becomes 23.
- Thus, \( \sqrt{529} = 23 \).
These methods are effective for finding square roots without a calculator and help in understanding the underlying principles of square roots.
Square Root Properties
The properties of square roots are fundamental to understanding and working with square roots in mathematics. These properties help simplify complex expressions and solve equations involving square roots. Here are some key properties of square roots:
- Non-Negativity: For any non-negative number \( a \), the square root is always non-negative. This means \(\sqrt{a} \geq 0\).
- Product Property: The square root of a product is equal to the product of the square roots of the factors. Mathematically, \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and denominator. This is expressed as \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), where \( b \neq 0 \).
- Square of a Square Root: The square of the square root of a number returns the original number, i.e., \((\sqrt{a})^2 = a\).
- Additive Property Limitation: Unlike multiplication and division, the square root of a sum is not equal to the sum of the square roots. In other words, \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\).
- Rational and Irrational Numbers: The square root of a perfect square (e.g., 1, 4, 9, 16) is rational, while the square root of a non-perfect square is irrational.
These properties are essential tools in algebra and higher-level mathematics, aiding in the simplification of expressions and the solving of equations. Understanding and applying these properties can make complex mathematical problems more manageable.

Simplifying Square Roots
Simplifying square roots involves breaking down a number into its prime factors and simplifying the expression by taking out perfect square factors. Here is a step-by-step guide to simplify square roots:
- Break down the number inside the square root into its prime factors. For example, \( \sqrt{48} \) can be expressed as \( \sqrt{16 \times 3} \).
- Identify the perfect square factors and simplify each of them separately. In the example \( \sqrt{48} \), we have \( \sqrt{16} \) and \( \sqrt{3} \).
- Take the square root of the perfect square factor. Here, \( \sqrt{16} = 4 \). Therefore, \( \sqrt{48} \) simplifies to \( 4\sqrt{3} \).
If the number inside the square root does not contain any perfect squares, it cannot be simplified further. For instance, \( \sqrt{19} \) remains as it is.
To simplify the square root of a fraction, simplify the numerator and denominator separately. Then, simplify the entire fraction if possible. For example, \( \sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3} \).
Memorizing the perfect squares up to 100 can greatly aid in simplifying square roots. Practice with various problems to become proficient in this method.
| Perfect Square | Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
Square Roots of Fractions
Finding the square root of a fraction involves understanding the square root properties and applying them to both the numerator and the denominator. The square root of a fraction is the same as the fraction of the square roots of the numerator and the denominator. Here is a detailed step-by-step process:
Consider a fraction \( \frac{a}{b} \). To find the square root of this fraction:
- Find the square root of the numerator \( \sqrt{a} \).
- Find the square root of the denominator \( \sqrt{b} \).
- Combine the results to form \( \frac{\sqrt{a}}{\sqrt{b}} \).
Here is an example to illustrate this process:
- Example: Find the square root of \( \frac{9}{16} \).
- Step 1: Find the square root of 9: \( \sqrt{9} = 3 \).
- Step 2: Find the square root of 16: \( \sqrt{16} = 4 \).
- Step 3: Combine the results: \( \sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4} \).
Here are some common examples and their solutions:
| Fraction | Square Root of Numerator | Square Root of Denominator | Square Root of Fraction |
|---|---|---|---|
| \( \frac{4}{25} \) | \( \sqrt{4} = 2 \) | \( \sqrt{25} = 5 \) | \( \frac{2}{5} \) |
| \( \frac{1}{9} \) | \( \sqrt{1} = 1 \) | \( \sqrt{9} = 3 \) | \( \frac{1}{3} \) |
| \( \frac{49}{64} \) | \( \sqrt{49} = 7 \) | \( \sqrt{64} = 8 \) | \( \frac{7}{8} \) |
When dealing with more complex fractions, the same principles apply. For fractions that are not perfect squares, the square roots can often be simplified further:
- Example: Simplify \( \sqrt{\frac{50}{72}} \).
- Step 1: Simplify the fraction if possible: \( \frac{50}{72} = \frac{25}{36} \).
- Step 2: Find the square root of the numerator: \( \sqrt{25} = 5 \).
- Step 3: Find the square root of the denominator: \( \sqrt{36} = 6 \).
- Step 4: Combine the results: \( \sqrt{\frac{50}{72}} = \sqrt{\frac{25}{36}} = \frac{5}{6} \).
Practice these steps with different fractions to become comfortable with the process of finding square roots of fractions. Below are some practice problems:
- Find the square root of \( \frac{16}{81} \).
- Find the square root of \( \frac{36}{49} \).
- Find the square root of \( \frac{100}{121} \).
- Find the square root of \( \frac{144}{169} \).
- Simplify \( \sqrt{\frac{75}{200}} \).
Square Roots of Decimals
Finding the square root of a decimal follows similar steps as finding the square root of a whole number. The key difference is in handling the decimal point. Here is a step-by-step method to find the square root of a decimal.
- Convert the Decimal: If the decimal is not a perfect square, convert it into a fraction. For example, 0.25 can be written as \( \frac{25}{100} \) or \( \frac{1}{4} \).
- Separate the Numerator and Denominator: Find the square root of the numerator and the denominator separately. Using our example: \[ \sqrt{0.25} = \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2} = 0.5 \]
- Direct Calculation: For decimals that are perfect squares, find the square root directly. Examples include: \[ \sqrt{0.04} = 0.2 \quad \text{(since \(0.2 \times 0.2 = 0.04\))} \] \[ \sqrt{0.81} = 0.9 \quad \text{(since \(0.9 \times 0.9 = 0.81\))} \]
- Using Long Division Method: For more complex decimals, the long division method can be used. Here’s an example for \( \sqrt{0.36} \):
- Pair the digits from the decimal point, i.e., 0.36 → 36
- Find the largest number whose square is less than or equal to 36, which is 6 (since \(6 \times 6 = 36\)).
- The square root of 0.36 is 0.6.
- Verification: Verify the result by squaring the obtained value to check if it matches the original decimal. For instance, \(0.6 \times 0.6 = 0.36\).
Practice Problems:
- \(\sqrt{0.49} = 0.7\)
- \(\sqrt{0.01} = 0.1\)
- \(\sqrt{0.09} = 0.3\)
- \(\sqrt{0.16} = 0.4\)
For more practice, here are additional problems:
| Decimal | Square Root |
|---|---|
| 0.25 | 0.5 |
| 0.64 | 0.8 |
| 0.81 | 0.9 |
| 0.04 | 0.2 |
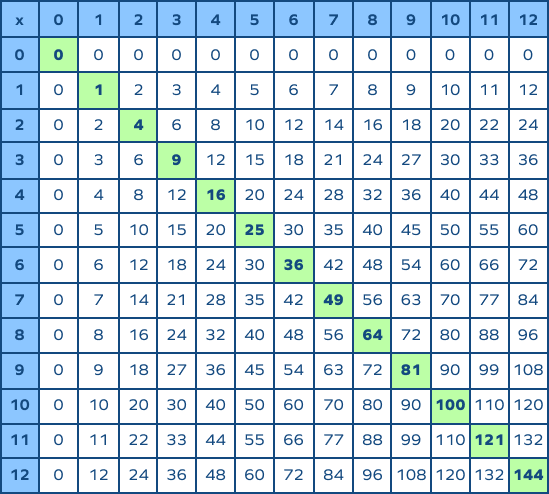
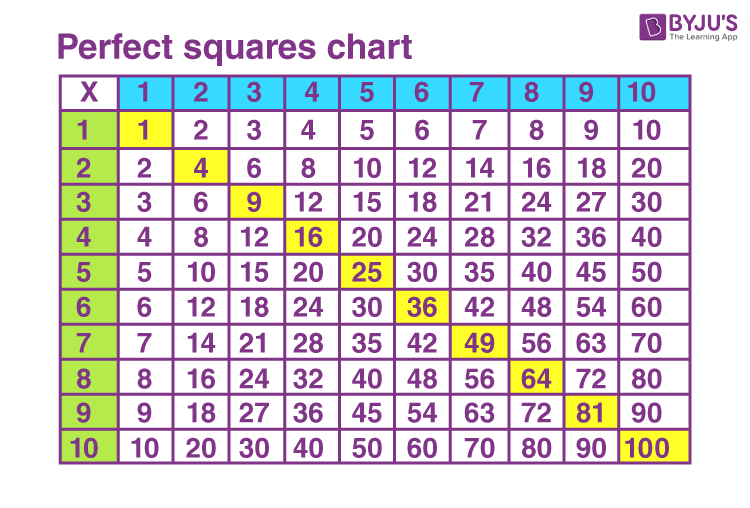
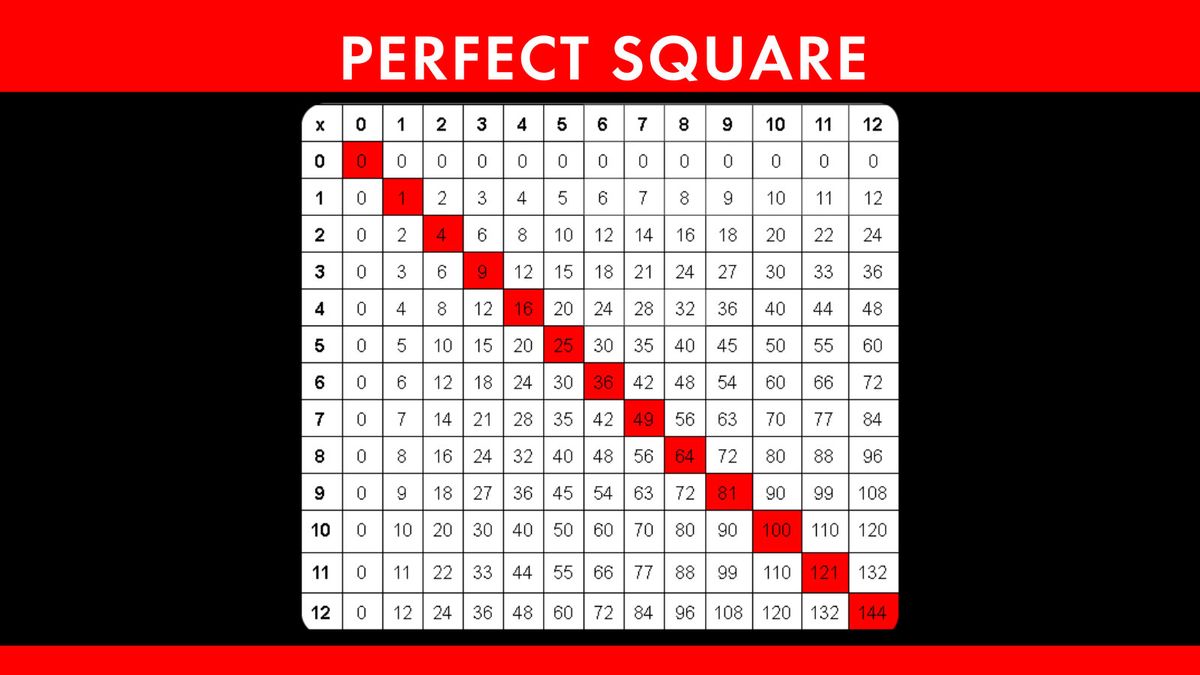
Perfect Squares
Perfect squares are numbers that can be expressed as the product of an integer with itself. For example, \(16\) is a perfect square because it can be written as \(4 \times 4\). This also means that the square root of a perfect square is always an integer.
Examples of Perfect Squares
Here are some examples of perfect squares:
- \(1 = 1 \times 1\)
- \(4 = 2 \times 2\)
- \(9 = 3 \times 3\)
- \(16 = 4 \times 4\)
- \(25 = 5 \times 5\)
- \(36 = 6 \times 6\)
- \(49 = 7 \times 7\)
- \(64 = 8 \times 8\)
- \(81 = 9 \times 9\)
- \(100 = 10 \times 10\)
Properties of Perfect Squares
- The square root of a perfect square is always an integer.
- Perfect squares are always non-negative.
- Perfect squares end with digits such as \(0, 1, 4, 5, 6,\) or \(9\) in base 10.
- The difference between consecutive perfect squares increases as the numbers increase.
Finding Perfect Squares
To find whether a number is a perfect square, you can try to find its square root. If the square root is an integer, the number is a perfect square. For example:
- \(\sqrt{49} = 7\) (since \(7\) is an integer, \(49\) is a perfect square)
- \(\sqrt{50} \approx 7.07\) (since this is not an integer, \(50\) is not a perfect square)
Visualizing Perfect Squares
Perfect squares can also be visualized as areas of squares with integer side lengths:
| Integer (n) | Perfect Square (n2) | Visual Representation |
|---|---|---|
| 1 | 1 | |
| 2 | 4 | |
| 3 | 9 | |
| 4 | 16 |
Practice Problems
Try to determine whether the following numbers are perfect squares:
- 64
- 72
- 81
- 90
- 100
Answers:
- \(64 = 8 \times 8\) (Perfect Square)
- \(72 \approx 8.49\) (Not a Perfect Square)
- \(81 = 9 \times 9\) (Perfect Square)
- \(90 \approx 9.49\) (Not a Perfect Square)
- \(100 = 10 \times 10\) (Perfect Square)

Square Root Calculation Methods
Calculating square roots can be approached through various methods. Here are some commonly used techniques:
- Prime Factorization Method:
- Factorize the number into its prime factors.
- Pair the prime factors.
- Take one number from each pair and multiply them.
Example: \( \sqrt{36} \)
Prime factorization of 36: \( 2 \times 2 \times 3 \times 3 \)
Pairs: \( (2 \times 2), (3 \times 3) \)
Square root: \( 2 \times 3 = 6 \)
- Long Division Method:
- Group the digits in pairs from right to left.
- Find the largest number whose square is less than or equal to the first pair.
- Subtract the square of this number from the first pair and bring down the next pair of digits.
- Double the number obtained and find a new digit to form the divisor.
- Repeat the process until all pairs are used.
Example: \( \sqrt{1521} \)
Steps: 1, 12, 123, ...
- Estimation Method:
- Find two perfect squares between which the number lies.
- Estimate the square root based on these values.
- Refine the estimate by averaging or using iterative methods.
Example: \( \sqrt{50} \)
50 lies between \( 7^2 (49) \) and \( 8^2 (64) \)
Estimate: 7.1
- Using a Calculator:
Most scientific calculators have a square root function. Simply input the number and press the square root button.
- Newton's Method:
- Choose an initial guess.
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \) where \( S \) is the number and \( x_n \) is the current estimate.
- Repeat until the desired accuracy is achieved.
Example: \( \sqrt{10} \)
Initial guess: 3
First iteration: \( \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667 \)
These methods provide various ways to find the square root of a number, each useful in different scenarios. Practice each method to understand its application and accuracy.
Worksheets and Practice Problems
Practicing square roots is essential for mastering this mathematical concept. Below are several worksheets and practice problems designed to help you understand and apply the principles of square roots effectively.
Worksheet 1: Finding Square Roots
This worksheet focuses on the basics of finding square roots of perfect squares.
- √64 =
- √81 =
- √144 =
Worksheet 2: Simplifying Square Roots
This worksheet helps you practice simplifying square roots by breaking them down into their prime factors.
- √50 =
- √72 =
- √98 =
Worksheet 3: Square Roots of Fractions
This worksheet provides practice problems for finding the square roots of fractions.
- √(1/4) =
- √(9/16) =
- √(25/36) =
Worksheet 4: Square Roots of Decimals
This worksheet covers finding the square roots of decimal numbers.
- √0.25 =
- √1.44 =
- √2.56 =
Practice Problems
- Find the square root of 169.
- Simplify √200.
- Calculate √(16/25).
- Determine √0.81.
Regular practice with these worksheets will enhance your skills and confidence in working with square roots. For more worksheets and detailed explanations, consider exploring additional resources and reference materials.
Square Root Quiz and Review
Test your understanding of square roots with this comprehensive quiz. Review your knowledge and reinforce concepts with the following questions:
- What is the square root of 25?
- Calculate the square root of 144.
- Find the square root of 0.04.
- What are the properties of square roots?
- Simplify the square root of 72.
After completing the quiz, review your answers and explanations provided below:
| Question | Answer | Explanation |
| 1 | 5 | The square root of 25 is 5 because 5 multiplied by itself equals 25. |
| 2 | 12 | The square root of 144 is 12 because 12 multiplied by itself equals 144. |
| 3 | 0.2 | The square root of 0.04 is 0.2 because 0.2 multiplied by itself equals 0.04. |
| 4 | Properties include the square of a negative number is positive, the square of 0 is 0, and the square of 1 is 1. | Various properties govern square roots, including those mentioned above. |
| 5 | 6√2 | The square root of 72 can be simplified to 6√2 by breaking down 72 into its prime factors. |
Continue practicing and exploring advanced applications of square roots to enhance your mathematical skills!
Answer Keys and Explanations
Check your answers and understand the solutions with the following detailed explanations:
| Question | Answer | Explanation |
| 1 | 5 | The square root of 25 is 5 because 5 multiplied by itself equals 25. |
| 2 | 12 | The square root of 144 is 12 because 12 multiplied by itself equals 144. |
| 3 | 0.2 | The square root of 0.04 is 0.2 because 0.2 multiplied by itself equals 0.04. |
| 4 | Properties include the square of a negative number is positive, the square of 0 is 0, and the square of 1 is 1. | Various properties govern square roots, including those mentioned above. |
| 5 | 6√2 | The square root of 72 can be simplified to 6√2 by breaking down 72 into its prime factors. |
Review these explanations to deepen your understanding of square roots and enhance your problem-solving skills!

Advanced Square Root Applications
Explore the versatility of square roots through these advanced applications:
- Root Mean Square (RMS) calculations in physics and engineering.
- Using square roots in geometry to find side lengths and areas of squares and rectangles.
- Applying square roots in financial mathematics for calculating compound interest and mortgage payments.
- Utilizing square roots in computer science algorithms, such as numerical methods and cryptography.
- Understanding the role of square roots in statistical analysis, including standard deviation and variance calculations.
These applications showcase the widespread utility of square roots across various disciplines, empowering you to apply mathematical concepts in real-world scenarios!
Related Mathematical Concepts
Expand your understanding of mathematical concepts related to square roots with the following:
- Exponents: Learn how exponents relate to square roots and their applications in algebra and calculus.
- Radicals: Explore the broader concept of radicals, including nth roots and their properties.
- Quadratic Equations: Understand how square roots play a crucial role in solving quadratic equations and graphing parabolas.
- Pythagorean Theorem: Discover the connection between square roots and the Pythagorean theorem in geometry.
- Trigonometry: Delve into trigonometric functions and their relationship with square roots, especially in right-angled triangles.
By exploring these related mathematical concepts, you'll deepen your mathematical knowledge and see how square roots fit into the broader landscape of mathematics!
Additional Resources and References
Expand your knowledge further with these additional resources and references:
- - Explore square roots with interactive explanations and examples.
- - Dive deeper into square roots with comprehensive tutorials and practice exercises.
- - Learn about radicals and their properties with clear explanations and worked examples.
- - Access lessons, quizzes, and videos to master square roots and related concepts.
These resources offer valuable insights and supplementary materials to enhance your understanding of square roots and related mathematical concepts!
Xem video Bình phương căn và căn bậc ba để học cách giải các bài tập về bình phương căn và câu hỏi liên quan.
Bình phương căn và căn bậc ba | Toán với Thầy J
READ MORE:
Xem video về cách đơn giản hóa căn bậc hai của một số không phải là bình phương để hiểu cách giải các bài tập liên quan đến căn bậc hai.
Cách đơn giản hóa căn bậc hai của một số không phải là bình phương