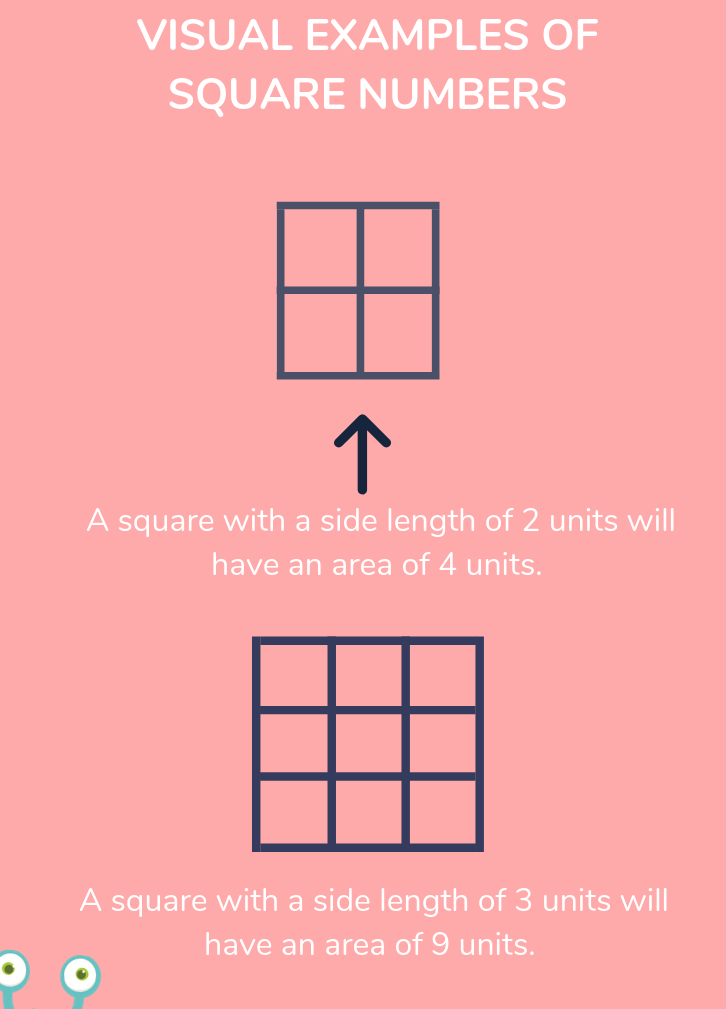Topic estimating square root worksheet: Estimating square roots can be challenging, but with our comprehensive worksheet, you'll master this essential math skill in no time. Our step-by-step guide and practice problems will help you understand and estimate square roots accurately, making math easier and more enjoyable. Start improving your estimation skills today!
Table of Content
- Estimating Square Roots Worksheet
- Introduction to Estimating Square Roots
- Importance of Estimating Square Roots in Mathematics
- Basic Concepts and Definitions
- Step-by-Step Guide to Estimating Square Roots
- Understanding Perfect Squares
- Techniques for Estimating Square Roots
- Examples of Estimating Square Roots
- Common Mistakes to Avoid
- Practice Problems and Solutions
- Interactive Worksheets and Activities
- Advanced Estimation Methods
- Real-World Applications of Square Root Estimation
- Additional Resources and References
- Conclusion and Next Steps
- YOUTUBE:
Estimating Square Roots Worksheet
Estimating square roots is a fundamental skill in mathematics, especially useful for students to understand the relationship between perfect squares and their roots. This worksheet provides a variety of problems to help students practice and master estimating square roots.
Objectives
- Improve estimation skills for square roots.
- Understand the concept of perfect squares.
- Apply estimation techniques to solve real-world problems.
Instructions
- Review the perfect squares up to 20.
- Use the perfect squares to estimate the square roots of non-perfect squares.
- Compare your estimates with the actual values to check accuracy.
Examples
To estimate the square root of 50:
- Identify the perfect squares around 50. The perfect squares are 49 (\(7^2\)) and 64 (\(8^2\)).
- Since 50 is closer to 49, estimate \(\sqrt{50}\) to be slightly more than 7.
- Using a more precise method, \(\sqrt{50} \approx 7.07\).
Practice Problems
| Problem | Estimate | Actual Value |
|---|---|---|
| \(\sqrt{10}\) | 3.2 | \(3.162\) |
| \(\sqrt{20}\) | 4.5 | \(4.472\) |
| \(\sqrt{30}\) | 5.5 | \(5.477\) |
| \(\sqrt{70}\) | 8.4 | \(8.367\) |
| \(\sqrt{90}\) | 9.5 | \(9.487\) |
Additional Resources

READ MORE:
Introduction to Estimating Square Roots
Estimating square roots is a valuable skill in mathematics that allows you to approximate the value of a square root without a calculator. This skill is particularly useful when dealing with non-perfect squares. By understanding and practicing estimation techniques, you can improve your number sense and enhance your problem-solving abilities.
To estimate the square root of a number, follow these steps:
- Identify the perfect squares that are closest to the given number. For example, to estimate \(\sqrt{50}\), recognize that 49 (\(7^2\)) and 64 (\(8^2\)) are the nearest perfect squares.
- Determine the square roots of these perfect squares. In this case, \(\sqrt{49} = 7\) and \(\sqrt{64} = 8\).
- Decide which perfect square is closer to the given number. Since 50 is closer to 49 than 64, estimate that \(\sqrt{50}\) is slightly more than 7.
- Refine your estimate by considering how much the given number exceeds the nearest lower perfect square. Here, 50 is 1 more than 49, so \(\sqrt{50}\) is slightly more than 7 but less than 8.
- Use a more precise method, if needed, to get a closer approximation. For instance, using the average method: \[ \sqrt{50} \approx \frac{7 + 8}{2} = 7.5 \] However, since 50 is closer to 49, the estimate should be slightly less than 7.5, approximately 7.1.
Practice these steps with different numbers to become proficient in estimating square roots. Below are some practice problems to help you get started:
| Number | Estimate | Actual Value |
|---|---|---|
| \(\sqrt{10}\) | 3.2 | 3.162 |
| \(\sqrt{20}\) | 4.5 | 4.472 |
| \(\sqrt{30}\) | 5.5 | 5.477 |
| \(\sqrt{70}\) | 8.4 | 8.367 |
| \(\sqrt{90}\) | 9.5 | 9.487 |
Importance of Estimating Square Roots in Mathematics
Estimating square roots is a crucial skill in mathematics that extends beyond classroom learning. It helps students develop a strong number sense and a deeper understanding of the relationships between numbers. Here are several reasons why estimating square roots is important:
- Enhances Number Sense: Estimating square roots improves a student’s ability to comprehend and work with numbers, fostering an intuitive grasp of numerical relationships and magnitudes.
- Facilitates Mental Math: By mastering square root estimation, students can perform calculations more quickly and accurately without relying on calculators, which is especially useful in timed tests and real-world scenarios.
- Builds Foundational Skills: Understanding how to estimate square roots lays the groundwork for more advanced mathematical concepts, such as algebra, geometry, and calculus.
- Solves Real-World Problems: Many practical applications in fields like engineering, physics, and finance require the ability to estimate square roots, making it a valuable skill for future careers.
- Boosts Confidence: Successfully estimating square roots can increase a student's confidence in their mathematical abilities, encouraging further learning and exploration.
Here’s how you can integrate square root estimation into your learning process:
- Practice Regularly: Consistent practice with different numbers helps reinforce the techniques and improves accuracy.
- Use Real-Life Examples: Apply square root estimation to everyday situations, such as measuring areas or understanding distances, to see its practical value.
- Collaborate and Discuss: Work with peers to solve estimation problems and discuss different approaches to find the most efficient methods.
- Challenge Yourself: Try estimating square roots of larger or more complex numbers to push your skills further.
By appreciating the importance of estimating square roots and practicing regularly, students can enhance their mathematical proficiency and prepare themselves for more advanced studies and real-world applications.
Basic Concepts and Definitions
Understanding the basic concepts and definitions related to square roots is essential before diving into estimation techniques. Below are key terms and ideas that form the foundation of square root estimation:
Square Root
The square root of a number \(x\) is a value \(y\) such that \(y^2 = x\). In other words, \(y\) is the number that, when multiplied by itself, equals \(x\). The square root is denoted by the radical symbol \(\sqrt{}\). For example, \(\sqrt{16} = 4\) because \(4 \times 4 = 16\).
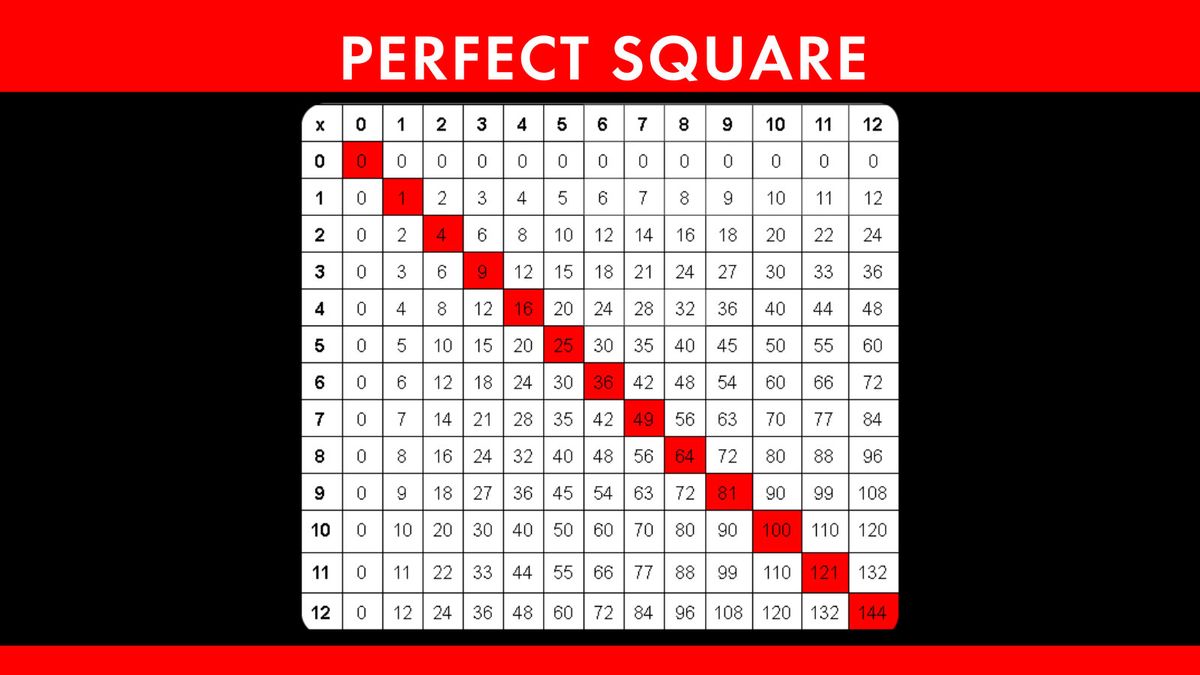
Perfect Squares
A perfect square is a number that is the square of an integer. Examples of perfect squares include:
- 1 (\(1^2\))
- 4 (\(2^2\))
- 9 (\(3^2\))
- 16 (\(4^2\))
- 25 (\(5^2\))
- 36 (\(6^2\))
- 49 (\(7^2\))
- 64 (\(8^2\))
- 81 (\(9^2\))
- 100 (\(10^2\))
Non-Perfect Squares
Non-perfect squares are numbers that do not have an integer as their square root. Examples include 2, 3, 5, 7, and 10. The square roots of these numbers are irrational, meaning they cannot be expressed as a simple fraction and their decimal representation is non-repeating and non-terminating. For example, \(\sqrt{2} \approx 1.414\) and \(\sqrt{3} \approx 1.732\).
Estimating Square Roots
Estimating the square root of a non-perfect square involves identifying the nearest perfect squares and using them to approximate the value. Here is a step-by-step process:
- Identify the Nearest Perfect Squares: Determine the perfect squares closest to the given number. For instance, for \(\sqrt{27}\), the nearest perfect squares are 25 (\(5^2\)) and 36 (\(6^2\)).
- Determine the Square Roots: Find the square roots of these perfect squares. In this case, \(\sqrt{25} = 5\) and \(\sqrt{36} = 6\).
- Approximate the Value: Since 27 is closer to 25 than to 36, \(\sqrt{27}\) is slightly more than 5. A more refined estimate can be calculated by interpolation, if necessary.
Interpolation
Interpolation is a method used to refine the estimate of a square root by considering the proportion between the nearest perfect squares. For example, if estimating \(\sqrt{27}\):
- Determine the difference between 27 and the nearest lower perfect square: \(27 - 25 = 2\).
- Determine the range between the nearest perfect squares: \(36 - 25 = 11\).
- Calculate the proportion: \(2 / 11 \approx 0.18\).
- Add this proportion to the lower square root: \(5 + 0.18 \approx 5.18\).
Thus, \(\sqrt{27} \approx 5.18\).
By understanding these basic concepts and definitions, you can build a strong foundation for accurately estimating square roots and improving your overall mathematical skills.
Step-by-Step Guide to Estimating Square Roots
Estimating square roots is a valuable skill, especially when you don't have a calculator handy. Here's a step-by-step guide to help you estimate square roots accurately.
-
Identify the Perfect Squares:
First, recognize the perfect squares that are close to the number you're estimating the square root of. For example, if you're estimating the square root of 20, you should know that 16 (42) and 25 (52) are the closest perfect squares.
-
Find the Interval:
Determine the interval between which your number lies. Using the previous example, 20 lies between 16 and 25, so:
\(4^2 < 20 < 5^2\)
This means \(\sqrt{20}\) is between 4 and 5.
-
Estimate Closer:
To get a more precise estimate, consider how close the number is to the nearest perfect squares. Since 20 is closer to 16 than to 25, the square root of 20 will be slightly more than 4 but less than 4.5.
-
Use Averaging (Optional):
If you want an even closer approximation, you can use the averaging method. For example, let's estimate \(\sqrt{20}\) by averaging 4 and 5:
\[\text{Average} = \frac{4 + 5}{2} = 4.5\]
Since \(4.5^2 = 20.25\), which is slightly higher than 20, try a number slightly lower than 4.5, such as 4.4:
\(4.4^2 = 19.36\)
Since 19.36 is closer to 20 than 20.25, 4.4 is a good estimate for \(\sqrt{20}\).
-
Refine the Estimate:
Continue refining your estimate by testing numbers slightly higher or lower until you reach an acceptable level of accuracy. For example, you might find:
\(4.45^2 = 19.8025\)
And \(4.48^2 = 20.0704\), so \(\sqrt{20}\) is approximately 4.47.
Using these steps, you can estimate square roots for numbers that are not perfect squares. This process helps develop a strong number sense and is particularly useful in various real-world applications.
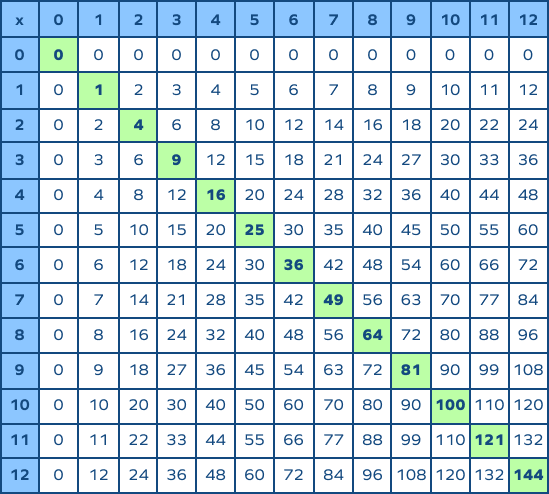
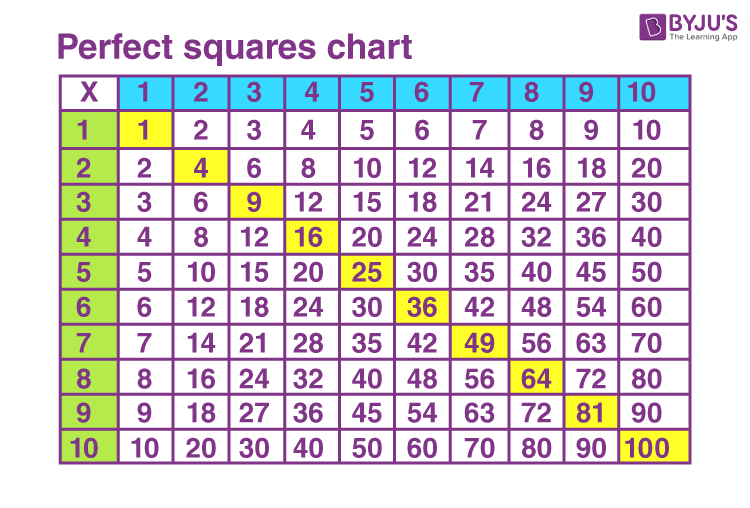
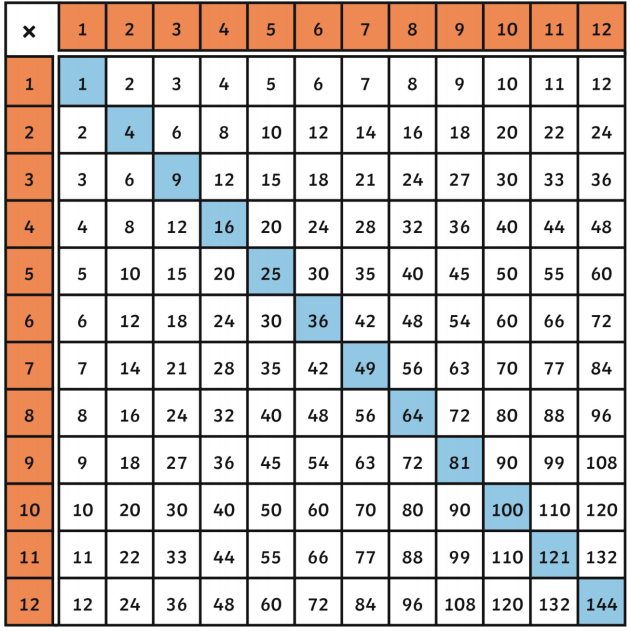
Understanding Perfect Squares
A perfect square is a number that can be expressed as the product of an integer with itself. In other words, if \( n \) is an integer, then \( n^2 \) (read as "n squared") is a perfect square. Understanding perfect squares is essential when estimating square roots, as they serve as reference points.
Properties of Perfect Squares
- A perfect square always has a non-negative square root.
- The square of an integer is always a perfect square.
- The square root of a perfect square is always an integer.
Examples of Perfect Squares
| Integer | Perfect Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
Finding Perfect Squares
- Select an integer \( n \).
- Multiply the integer by itself: \( n \times n \).
- The result is the perfect square: \( n^2 \).
Recognizing Perfect Squares
Recognizing perfect squares is crucial for estimating square roots. If you know that \( 16 \) is a perfect square (since \( 4 \times 4 = 16 \)), you can easily identify that the square root of \( 16 \) is \( 4 \).
Using Perfect Squares in Estimation
When estimating the square root of a non-perfect square, find the two closest perfect squares between which the number lies. For example, to estimate \( \sqrt{50} \):
- Identify the nearest perfect squares: \( 49 \) (since \( 7 \times 7 = 49 \)) and \( 64 \) (since \( 8 \times 8 = 64 \)).
- Since \( 50 \) is closer to \( 49 \), you can estimate that \( \sqrt{50} \) is slightly greater than \( 7 \).
Practice Problems
To reinforce your understanding, practice identifying and working with perfect squares. Solve the following problems:
- What is the perfect square of \( 12 \)?
- Identify the square root of \( 121 \).
- Between which two perfect squares does \( 75 \) lie?
Answers:
- \( 12^2 = 144 \)
- \( \sqrt{121} = 11 \)
- \( 75 \) lies between \( 64 \) and \( 81 \) (since \( 8 \times 8 = 64 \) and \( 9 \times 9 = 81 \)).
Techniques for Estimating Square Roots
Estimating square roots is a useful skill, especially when a number is not a perfect square. Below are several techniques to help you estimate square roots accurately.
Technique 1: Using Perfect Squares
To estimate the square root of a number, find the two closest perfect squares between which the number lies. For example:
- To estimate \(\sqrt{50}\), note that \(7^2 = 49\) and \(8^2 = 64\). Thus, \(\sqrt{50}\) is between 7 and 8.
- To estimate \(\sqrt{120}\), note that \(10^2 = 100\) and \(11^2 = 121\). Thus, \(\sqrt{120}\) is between 10 and 11.
Technique 2: Averaging
Once you identify the two closest perfect squares, you can average them for a better estimate:
- For \(\sqrt{50}\), since 49 and 64 are close, average 7 and 8 to get \(7.5\) as an initial estimate. Refine by checking \((7.5)^2\).
- For \(\sqrt{120}\), average 10 and 11 to get \(10.5\). Refine by checking \((10.5)^2\).
Technique 3: Number Line Method
Visualize the number on a number line to better approximate the square root:
- Mark the perfect squares on the number line.
- Place your number between the two closest perfect squares.
- Estimate the position of your number relative to the perfect squares to find a more accurate square root.
For example, placing \(\sqrt{26}\) on the number line between \(\sqrt{25}\) and \(\sqrt{36}\), you can see it is closer to 5 than to 6, so a good estimate is around \(5.1\).
Technique 4: Babylonian Method (Heron's Method)
This iterative method provides a very accurate estimate:
- Start with an initial guess. For \(\sqrt{50}\), a reasonable guess is 7.
- Use the formula: \( \text{New guess} = \frac{\text{Old guess} + \frac{\text{Number}}{\text{Old guess}}}{2} \).
- Repeat the process until the guesses converge. For \(\sqrt{50}\):
- First guess: \(7\).
- Second guess: \( \frac{7 + \frac{50}{7}}{2} \approx 7.071 \).
- Third guess: \( \frac{7.071 + \frac{50}{7.071}}{2} \approx 7.071 \).
Example Problems
Let's apply these techniques to a few examples:
| Number | Closest Perfect Squares | Estimate |
| 35 | 25 (\(5^2\)) and 36 (\(6^2\)) | Approximately 5.9 |
| 80 | 64 (\(8^2\)) and 81 (\(9^2\)) | Approximately 8.9 |
| 150 | 144 (\(12^2\)) and 169 (\(13^2\)) | Approximately 12.2 |
By practicing these techniques, you can become proficient in estimating square roots, which is a valuable skill for both academic and real-world problem-solving.
Examples of Estimating Square Roots
Estimating square roots is an important mathematical skill. Here are some detailed examples to help illustrate various methods for estimating square roots.
Example 1: Guess and Check Method
Problem: Estimate the square root of 20.
- Start with an initial guess: 4 (since \(4^2 = 16\)).
- Check: \(4^2 = 16\) (too low).
- Try a higher guess: 5 (since \(5^2 = 25\)).
- Check: \(5^2 = 25\) (too high).
- Refine the guess: Try 4.5.
- Check: \(4.5^2 = 20.25\) (slightly high but very close).
Result: The square root of 20 is approximately 4.5.
Example 2: Prime Factorization Method
Problem: Estimate the square root of 72.
- Perform prime factorization: \(72 = 2^3 \times 3^2\).
- Group the prime factors into pairs: \((2 \times 2), 2, (3 \times 3)\).
- Calculate the square root: \(2 \times 3 = 6\), with the remaining 2 staying under the root.
Result: The square root of 72 is \(6\sqrt{2}\).
Example 3: Using the Long Division Method
Problem: Estimate the square root of 50.
- Group the digits in pairs starting from the decimal point: 50.00 becomes 50.
- Find the largest number whose square is less than or equal to 50: \(7^2 = 49\).
- Write 7 as the first digit of the square root.
- Subtract 49 from 50 to get 1.
- Bring down two zeros to make it 100.
- Double the current result (7) and find the next digit: 140 + 1 = 141.
- The next digit is approximately 1, giving 71 as the square root.
Result: The square root of 50 is approximately 7.1.
Example 4: Newton’s Method
Problem: Estimate the square root of 45 using Newton's Method.
- Start with an initial guess: \(x_0 = 6.5\).
- Use the formula: \(x_{n+1} = \frac{1}{2}(x_n + \frac{45}{x_n})\).
- First iteration: \(x_1 = \frac{1}{2}(6.5 + \frac{45}{6.5}) = 6.2\).
- Second iteration: \(x_2 = \frac{1}{2}(6.2 + \frac{45}{6.2}) \approx 6.1\).
Result: The square root of 45 is approximately 6.1.
Example 5: Estimation by Linear Interpolation
Problem: Estimate the square root of 24.
- Find the nearest perfect squares: 16 and 25 (4 and 5).
- Estimate: \(24\) is closer to \(25\), so guess between 4.8 and 4.9.
- Calculate and refine the estimate: \(4.8^2 = 23.04\), \(4.9^2 = 24.01\).
Result: The square root of 24 is approximately 4.9.
Common Mistakes to Avoid
When estimating square roots, it's important to be aware of common pitfalls that can lead to errors. Here are some common mistakes to avoid and tips to ensure accurate estimations:
-
Confusing Perfect Squares:
Ensure you accurately identify perfect squares. For example, mistaking 36 for 49 can lead to incorrect estimations.
-
Ignoring Intermediate Values:
When estimating non-perfect squares, don't ignore the values between perfect squares. For example, estimating √50 as 7 instead of closer to 7.1 because 50 is between 49 and 64.
-
Overlooking Precision:
Avoid rounding too early. Carry your calculations to an extra decimal place before rounding to the desired precision to avoid compounding errors.
-
Incorrect Square Root Operations:
Be careful with operations involving square roots, especially when simplifying expressions. Misapplying properties can lead to significant errors.
-
Not Checking Your Work:
Always verify your results by squaring your estimate to see if it approximates the original number closely. This helps catch any mistakes made during estimation.
-
Ignoring Negative Roots:
Remember that while estimating the principal (positive) square root is common, some contexts might require considering both positive and negative roots.
By being mindful of these common mistakes, you can improve your accuracy and confidence in estimating square roots.

Practice Problems and Solutions
Below are several practice problems to help you master the estimation of square roots. Each problem is followed by a step-by-step solution.
Problem 1
Estimate the square root of 50.
- Identify the two perfect squares between which 50 lies: 49 (72) and 64 (82).
- Since 50 is closer to 49, start with 7. Try 7.1, 7.2, etc. until the value squared is close to 50.
- Checking 7.1: \( 7.1 \times 7.1 = 50.41 \) (too high).
- Checking 7.0: \( 7.0 \times 7.0 = 49 \) (too low).
- Thus, \( \sqrt{50} \approx 7.1 \).
Problem 2
Estimate the square root of 85.
- Identify the two perfect squares between which 85 lies: 81 (92) and 100 (102).
- Since 85 is closer to 81, start with 9. Try 9.1, 9.2, etc. until the value squared is close to 85.
- Checking 9.2: \( 9.2 \times 9.2 = 84.64 \) (close to 85).
- Checking 9.3: \( 9.3 \times 9.3 = 86.49 \) (too high).
- Thus, \( \sqrt{85} \approx 9.2 \).
Problem 3
Estimate the square root of 120.
- Identify the two perfect squares between which 120 lies: 121 (112) and 144 (122).
- Since 120 is closer to 121, start with 11. Try 11.0, 11.1, etc. until the value squared is close to 120.
- Checking 11.0: \( 11.0 \times 11.0 = 121 \) (close to 120).
- Checking 10.9: \( 10.9 \times 10.9 = 118.81 \) (close to 120).
- Thus, \( \sqrt{120} \approx 10.9 \).
Problem 4
Estimate the square root of 200.
- Identify the two perfect squares between which 200 lies: 196 (142) and 225 (152).
- Since 200 is closer to 196, start with 14. Try 14.1, 14.2, etc. until the value squared is close to 200.
- Checking 14.1: \( 14.1 \times 14.1 = 198.81 \) (close to 200).
- Checking 14.2: \( 14.2 \times 14.2 = 201.64 \) (too high).
- Thus, \( \sqrt{200} \approx 14.1 \).
Problem 5
Estimate the square root of 75.
- Identify the two perfect squares between which 75 lies: 64 (82) and 81 (92).
- Since 75 is closer to 81, start with 9. Try 8.5, 8.6, etc. until the value squared is close to 75.
- Checking 8.6: \( 8.6 \times 8.6 = 73.96 \) (close to 75).
- Checking 8.7: \( 8.7 \times 8.7 = 75.69 \) (close to 75).
- Thus, \( \sqrt{75} \approx 8.7 \).
Practice these steps with different numbers to become proficient at estimating square roots!
Interactive Worksheets and Activities
Interactive worksheets and activities can make estimating square roots more engaging and effective for students. Here are a few activities you can incorporate into your lessons:
-
Number Line Activity
Print an oversized number line and have students place perfect and non-perfect square roots on it. This helps them visualize the relative positions of square roots and reinforces their understanding of perfect squares.
-
Square Root Concentration Game
Create a game where students match numbers with their estimated square roots. Use cards or digital tools to make this activity interactive and fun.
-
Targeted Feedback with SmartPals
Use SmartPals or similar tools to provide students with immediate feedback. Students solve estimation problems and get their answers checked by peers or teachers, encouraging collaborative learning.
-
Number Talk Anticipatory Set
Use small cubes to help students explore cube roots as an extension of square roots. This hands-on activity encourages teamwork and deeper understanding of roots.
-
Mathopolis Game
An online game where students practice estimating square roots. This game offers quick feedback and can be played competitively to make learning more engaging.
Incorporating these interactive activities into your lessons can help students grasp the concept of estimating square roots more effectively and enjoyably.
Advanced Estimation Methods
Estimating square roots can be done with greater accuracy using advanced methods. These techniques go beyond basic approximations and leverage mathematical concepts to achieve more precise results. Here, we will explore three advanced estimation methods: Newton's Method, the Babylonian Method, and Continued Fractions.
Newton's Method
Newton's Method, also known as the Newton-Raphson Method, is an iterative technique to find successively better approximations to the roots (or zeroes) of a real-valued function. For estimating square roots, the function \( f(x) = x^2 - N \) is used, where \( N \) is the number whose square root we want to find.
- Choose an initial guess \( x_0 \) (a reasonable starting point).
- Use the iteration formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{N}{x_n} \right) \).
- Repeat the iteration until the value stabilizes to a desired level of accuracy.
Example:
Estimate \( \sqrt{10} \) with an initial guess of \( x_0 = 3 \).
- \( x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667 \)
- \( x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) = 3.1623 \)
- \( x_3 = \frac{1}{2} \left( 3.1623 + \frac{10}{3.1623} \right) = 3.1623 \) (stabilized)
Babylonian Method
The Babylonian Method, also known as Heron's Method, is a special case of Newton's Method for square roots. It is one of the oldest known algorithms for computing square roots.
- Choose an initial guess \( x_0 \).
- Use the iteration formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{N}{x_n} \right) \).
- Repeat the iteration until the value converges.
This method is particularly effective for manual calculations.
Example:
Estimate \( \sqrt{20} \) with an initial guess of \( x_0 = 5 \).
- \( x_1 = \frac{1}{2} \left( 5 + \frac{20}{5} \right) = 4.5 \)
- \( x_2 = \frac{1}{2} \left( 4.5 + \frac{20}{4.5} \right) = 4.4722 \)
- \( x_3 = \frac{1}{2} \left( 4.4722 + \frac{20}{4.4722} \right) = 4.4721 \) (stabilized)
Continued Fractions
Continued fractions provide another approach to estimate square roots with high precision. A square root can be expressed as an infinite continued fraction.
For example, \( \sqrt{N} \) can be represented as:
\[
\sqrt{N} = a_0 + \frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{a_3 + \ddots}}}
\]
The coefficients \( a_n \) can be determined through specific formulas for each number. This method is more complex but offers a powerful tool for precise calculations.
Summary
Advanced methods for estimating square roots such as Newton's Method, the Babylonian Method, and Continued Fractions provide mathematicians and students with tools for achieving greater accuracy. By iterating through formulas and understanding the underlying mathematical concepts, these methods enhance our ability to estimate square roots with precision.
Real-World Applications of Square Root Estimation
Square root estimation is a valuable mathematical skill with numerous practical applications in various fields. Understanding how to estimate square roots can simplify complex calculations, aid in problem-solving, and enhance analytical thinking. Here are some real-world applications of square root estimation:
1. Architecture and Construction
Architects and construction workers frequently use square root estimation to determine dimensions and materials. For example, when designing a square or rectangular space, they may need to calculate the length of the diagonal using the Pythagorean theorem. Estimating square roots allows for quick, on-site calculations to ensure precision and efficiency.
2. Engineering
Engineers often rely on square root estimation for various calculations, such as determining the load-bearing capacity of materials, analyzing forces and stresses in structures, and designing electrical circuits. Accurate estimations help engineers make informed decisions and maintain safety standards.
3. Physics
In physics, square roots are used in formulas to calculate distances, velocities, and other quantities. For instance, the formula for the period of a pendulum involves the square root of its length. Estimating these square roots allows physicists to predict outcomes and understand natural phenomena more effectively.
4. Finance
Square root estimation is useful in finance for calculating interest rates, risk assessments, and investment returns. For example, the standard deviation, a measure of investment risk, involves square root calculations. Estimating these values helps financial analysts make quicker decisions without the need for precise calculations.
5. Medicine
In the medical field, square root estimation can be used to determine the correct dosages of medication based on body surface area, which is calculated using square roots. This ensures that patients receive appropriate and safe amounts of medication.
6. Computer Graphics
Square root estimation is essential in computer graphics for rendering images and animations. Algorithms that calculate distances, lighting, and object scaling often involve square root operations. Estimating these values allows for faster processing and more efficient graphics rendering.
7. Navigation and GPS
Navigation systems and GPS technology use square root calculations to determine distances between coordinates. Estimating these distances quickly helps in providing real-time directions and optimizing travel routes.
Example: Estimating the Distance between Two Points
To estimate the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) on a coordinate plane, we use the distance formula:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
By estimating the square root, we can quickly approximate the distance, which is especially useful in navigation and mapping applications.
Conclusion
Square root estimation is a fundamental skill with diverse applications in everyday life and various professional fields. By mastering this technique, individuals can enhance their problem-solving abilities and improve their efficiency in numerous tasks.
Additional Resources and References
To further enhance your understanding and practice of estimating square roots, here are some valuable resources and references that provide comprehensive materials and activities:
-
Math Worksheets 4 Kids
Offers a wide range of printable square root worksheets, including exercises on finding square roots of integers, fractions, and decimals. These worksheets cater to students from 6th to 8th grade and include both simple and advanced problems.
-
Education.com
Provides interactive worksheets specifically designed for estimating square roots. These resources are aimed at 8th-grade students and help them practice estimating non-perfect square roots through engaging activities.
-
Brighterly
Features printable square root worksheets that are designed to be both educational and enjoyable. Brighterly’s resources include step-by-step approaches from simple to complex problems, making them ideal for young learners.
-
Math in English
Contains a variety of square root worksheets suitable for grades 6 and 7. These worksheets cover finding square roots, adding, subtracting, multiplying, and dividing square roots, as well as estimating roots of non-perfect squares.
-
Homeschool Math
Allows you to create customized square root worksheets, including options for simple calculations or more complex operations. The site offers both PDF and HTML formats.
These resources provide a mix of printable worksheets, interactive activities, and customizable options to support diverse learning needs. By utilizing these tools, students can gain a stronger grasp of estimating square roots and apply their knowledge effectively in various contexts.
Conclusion and Next Steps
Understanding and estimating square roots is a vital skill in mathematics, useful in various academic and real-world scenarios. By mastering the techniques of square root estimation, students can enhance their number sense and problem-solving abilities. This comprehensive guide has provided you with the foundational knowledge and advanced methods needed to estimate square roots accurately.
To conclude, let’s summarize the key points covered in this guide:
- The importance of estimating square roots and its applications in mathematics.
- Basic concepts and definitions related to square roots.
- Step-by-step methods for estimating square roots.
- Understanding perfect squares and their role in estimation.
- Various techniques for estimating square roots, including interpolation and approximation.
- Examples to illustrate the estimation process and common mistakes to avoid.
- Practice problems and interactive worksheets to reinforce learning.
- Advanced estimation methods for more precise calculations.
- Real-world applications of square root estimation.
- Additional resources and references for further learning.
Next steps to continue your learning journey:
- Practice Regularly: Consistent practice is key to mastering square root estimation. Utilize the worksheets and practice problems provided in this guide to hone your skills.
- Explore Further Resources: Dive into the additional resources and references section to explore more advanced topics and related mathematical concepts.
- Apply in Real-World Scenarios: Try to identify real-life situations where estimating square roots can be beneficial. This will help you understand the practical applications and importance of this skill.
- Seek Help if Needed: If you encounter difficulties, do not hesitate to seek help from teachers, tutors, or online forums. Collaborative learning can often provide new insights and solutions.
By following these steps, you will not only improve your square root estimation skills but also develop a deeper appreciation for mathematics. Keep practicing, stay curious, and continue to challenge yourself with more complex problems and applications. Mathematics is a journey of continuous learning and discovery, and your efforts will pay off in both academic and everyday contexts.
Ước Lượng Căn Bậc Hai - Hướng Dẫn Toàn Diện