Square Root of 40 Simplified: Easy Step-by-Step Guide

The process of simplifying the square root of 40 involves finding the prime factors and then simplifying the radical expression. Let's break down the steps to simplify \(\sqrt{40}\) in a clear and detailed manner.

Step-by-Step Simplification

1. Find the prime factorization of 40:

   \[
   40 = 2 \times 20 = 2 \times 2 \times 10 = 2 \times 2 \times 2 \times 5 = 2^3 \times 5
   \]

2. Express the square root of 40 using its prime factors:

   \[
   \sqrt{40} = \sqrt{2^3 \times 5}
   \]

3. Group the prime factors in pairs to simplify:

   \[
   \sqrt{2^3 \times 5} = \sqrt{2^2 \times 2 \times 5} = \sqrt{(2^2) \times 2 \times 5}
   \]

4. Simplify the square root by taking out the pairs:

   \[
   \sqrt{(2^2) \times 2 \times 5} = 2 \sqrt{2 \times 5} = 2 \sqrt{10}
   \]

Conclusion

The simplified form of the square root of 40 is:

\[
\sqrt{40} = 2\sqrt{10}
\]

Therefore, \(\sqrt{40}\) simplifies to \(2\sqrt{10}\). This process can be applied to other square roots by finding their prime factors and simplifying in a similar manner.

Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, yields the original number. For instance, the square root of 40 is the number that, when squared, equals 40. Mathematically, this is represented as \( \sqrt{40} \).

The process of finding the square root involves several methods, such as prime factorization and long division. Understanding square roots is crucial for solving various mathematical problems and is a foundational skill in algebra and geometry.

• Prime Factorization: To simplify \( \sqrt{40} \), we first find the prime factors of 40. These are \( 2^3 \times 5 \). Thus, \( \sqrt{40} \) can be written as \( \sqrt{2^2 \times 2 \times 5} \), which simplifies to \( 2\sqrt{10} \).
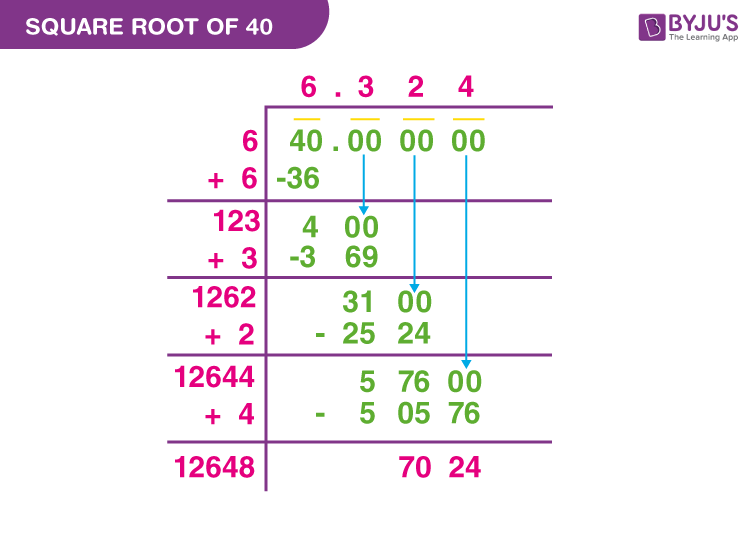
• Long Division Method: This method involves dividing the number into smaller parts and finding a sequence of digits that, when squared, approximate the original number. For 40, this process yields approximately 6.3246.

Square roots also have significant applications in various fields such as physics, engineering, and finance. They are used to solve quadratic equations, calculate areas and volumes, and in many other practical and theoretical scenarios.

To sum up, mastering the concept of square roots is essential for progressing in mathematics and understanding more complex mathematical theories and applications.

Square roots are mathematical expressions used to determine a number which, when multiplied by itself, gives the original number. For example, the square root of 40 is the number that, when squared, equals 40. This can be represented as \( \sqrt{40} \).

To simplify square roots, we need to find the simplest radical form. This involves identifying and factoring out the perfect squares within the original number. Let's go through the steps of simplifying \( \sqrt{40} \) in detail:

1. List the factors of 40: 1, 2, 4, 5, 8, 10, 20, 40.
2. Identify the perfect squares from the list: 1, 4.
3. Divide 40 by the largest perfect square: \( 40 \div 4 = 10 \).
4. Calculate the square root of the largest perfect square: \( \sqrt{4} = 2 \).
5. Combine the results: \( \sqrt{40} = 2 \sqrt{10} \).

Thus, the simplified form of \( \sqrt{40} \) is \( 2 \sqrt{10} \). This method of simplification is essential in many areas of mathematics, including algebra and geometry, as it allows for easier manipulation and understanding of expressions involving square roots.

For further clarity, let's look at the prime factorization method:

1. Find the prime factors of 40: \( 2 \times 2 \times 2 \times 5 \).
2. Group the prime factors into pairs: \( (2 \times 2) \times (2 \times 5) \).
3. Take the square root of each pair: \( \sqrt{(2 \times 2) \times (2 \times 5)} = \sqrt{2^2 \times 10} \).
4. Simplify the expression: \( 2 \sqrt{10} \).

This confirms that the simplest radical form of \( \sqrt{40} \) is indeed \( 2 \sqrt{10} \). Understanding and applying these steps to simplify square roots will enhance your mathematical problem-solving skills and help in solving complex equations more efficiently.

The prime factorization method is a straightforward and efficient way to simplify square roots. This method involves breaking down the number into its prime factors, pairing the same prime factors, and then simplifying. Here is a detailed, step-by-step guide to simplifying the square root of 40 using the prime factorization method:

1. Prime Factorization of the Number:

   First, we find the prime factors of 40.

   \(40 = 2 \times 2 \times 2 \times 5\)

2. Pairing the Prime Factors:

   Next, we pair the same prime factors together.

   \(40 = (2 \times 2) \times 2 \times 5\)

3. Extracting One Prime Factor from Each Pair:

   We take one prime factor from each pair.

   \( \sqrt{40} = \sqrt{(2 \times 2) \times 2 \times 5} = 2 \sqrt{2 \times 5} = 2 \sqrt{10}\)

Thus, the simplified form of the square root of 40 is \(2 \sqrt{10}\).

Example Problems

• Example 1: Square Root of 16
  1. Prime Factorization: \(16 = 2 \times 2 \times 2 \times 2\)
  2. Pairing the Prime Factors: \((2 \times 2) \times (2 \times 2)\)
  3. Extracting One Prime Factor from Each Pair: \(2 \times 2 = 4\)

  So, \( \sqrt{16} = 4\).

• Example 2: Square Root of 81
  1. Prime Factorization: \(81 = 3 \times 3 \times 3 \times 3\)
  2. Pairing the Prime Factors: \((3 \times 3) \times (3 \times 3)\)
  3. Extracting One Prime Factor from Each Pair: \(3 \times 3 = 9\)

  So, \( \sqrt{81} = 9\).

• Example 3: Square Root of 100
  1. Prime Factorization: \(100 = 2 \times 2 \times 5 \times 5\)
  2. Pairing the Prime Factors: \((2 \times 2) \times (5 \times 5)\)
  3. Extracting One Prime Factor from Each Pair: \(2 \times 5 = 10\)

  So, \( \sqrt{100} = 10\).

To simplify the square root of 40, we can use the prime factorization method. Here is a detailed, step-by-step guide:

1. List the prime factors of 40:

   The prime factorization of 40 is:

   40 = 2 × 2 × 2 × 5

2. Group the prime factors into pairs:

   Group the prime factors in pairs of the same numbers:

   \(\sqrt{40} = \sqrt{(2 \times 2) \times 2 \times 5}\)

3. Simplify the grouped pairs:

   The square root of a pair of 2's is 2, so we can simplify:

   \(\sqrt{(2 \times 2) \times 2 \times 5} = 2 \times \sqrt{2 \times 5}\)

   \(\sqrt{2 \times 5}\) can be written as \(\sqrt{10}\), so we have:

   \(2 \sqrt{10}\)

Thus, the simplified form of the square root of 40 is:

\(\sqrt{40} = 2 \sqrt{10}\)

This method can be applied to other non-perfect square numbers as well, using their prime factorization to simplify the square roots.

Let's explore the process of simplifying other square roots using similar methods as we did with the square root of 40. Here are a few examples:

Example 1: Simplifying √50

1. Find the prime factors of 50:
   • 50 = 2 × 5 × 5
2. Group the factors into pairs:
   • 50 = 2 × (5 × 5)
3. Simplify the square root:
   • √50 = √(2 × 5²) = 5√2

Example 2: Simplifying √72

1. Find the prime factors of 72:
   • 72 = 2 × 2 × 2 × 3 × 3
2. Group the factors into pairs:
   • 72 = (2 × 2) × (3 × 3) × 2
3. Simplify the square root:
   • √72 = √(2² × 3² × 2) = 2 × 3√2 = 6√2

Example 3: Simplifying √98

1. Find the prime factors of 98:
   • 98 = 2 × 7 × 7
2. Group the factors into pairs:
   • 98 = 2 × (7 × 7)
3. Simplify the square root:
   • √98 = √(2 × 7²) = 7√2

Example 4: Simplifying √18

1. Find the prime factors of 18:
   • 18 = 2 × 3 × 3
2. Group the factors into pairs:
   • 18 = 2 × (3 × 3)
3. Simplify the square root:
   • √18 = √(2 × 3²) = 3√2

Example 5: Simplifying √200

1. Find the prime factors of 200:
   • 200 = 2 × 2 × 2 × 5 × 5
2. Group the factors into pairs:
   • 200 = (2 × 2) × (5 × 5) × 2
3. Simplify the square root:
   • √200 = √(2² × 5² × 2) = 2 × 5√2 = 10√2

By following these steps, you can simplify any square root by using the prime factorization method and identifying pairs of factors. Practice these examples to become more comfortable with the process.

Simplified square roots find applications in various real-life scenarios across different fields. Here are some notable examples:

• Finance: Square roots are used to calculate the standard deviation in finance, which helps measure the volatility or risk of an investment. For instance, the volatility of a stock is determined by taking the square root of the variance of its returns.
• Architecture and Engineering: In construction and engineering, square roots are essential in determining the dimensions and stability of structures. The Pythagorean theorem, which involves square roots, is used to calculate distances and ensure the integrity of buildings, bridges, and other structures.
• Science: Square roots are used in various scientific calculations. For example, they are used to determine the root mean square (RMS) value in physics, which helps in analyzing waveforms and signals.
• Statistics: In statistics, square roots are used to calculate standard deviation, a measure of the amount of variation or dispersion in a set of values. This helps statisticians understand data distributions and make informed decisions.
• Computer Graphics: In computer graphics, square roots are used to calculate distances between points in 2D and 3D spaces. This is crucial for rendering images, modeling objects, and creating animations.
• Navigation: Square roots are used in navigation to calculate the shortest distance between two points on a map. This is particularly useful in GPS technology, where accurate distance measurements are critical.
• Cryptography: Cryptographic algorithms often involve square roots to ensure secure communication. For example, certain encryption methods use square roots to generate keys for encrypting and decrypting data.
• Photography: The f-number of a camera lens, which controls the aperture and hence the exposure, is related to the square root of the light-gathering area of the lens. This affects the depth of field and overall image quality.

These applications demonstrate how fundamental the concept of square roots is to various practical and theoretical fields, underscoring its importance in everyday problem-solving and technological advancements.

Simplifying square roots can sometimes lead to errors if certain common pitfalls are not avoided. Below are some common mistakes and how to avoid them:

• Incorrect Addition under the Square Root:

  A frequent error is assuming that the square root of a sum is the sum of the square roots:

  \(\sqrt{a + b} \ne \sqrt{a} + \sqrt{b}\)

  For example, \(\sqrt{9 + 16} \ne \sqrt{9} + \sqrt{16}\). The correct approach is to find the sum first and then take the square root: \(\sqrt{25} = 5\), not \(3 + 4 = 7\).

• Misapplying the Distributive Property:

  When simplifying expressions involving multiplication inside a square root, it is important to correctly apply the distributive property:

  \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)

  For example, \(\sqrt{4 \cdot 25} = \sqrt{4} \cdot \sqrt{25} = 2 \cdot 5 = 10\), not \(\sqrt{4} + \sqrt{25} = 2 + 5 = 7\).

• Incorrect Factorization:

  Ensure the number inside the square root is properly factored into its prime components. For instance, to simplify \(\sqrt{72}\):

  1. Find the prime factors of 72: \(72 = 2 \times 2 \times 2 \times 3 \times 3\).
  2. Pair the factors: \(\sqrt{72} = \sqrt{(2 \times 2) \times (2 \times 3 \times 3)} = \sqrt{4 \times 18}\).
  3. Simplify using the rule \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\): \(\sqrt{72} = \sqrt{4} \times \sqrt{18} = 2 \times 3\sqrt{2} = 6\sqrt{2}\).
• Failure to Combine Like Terms:

  When simplifying, remember to combine like terms. For instance, when adding square roots: \(2\sqrt{3} + 3\sqrt{3} = (2 + 3)\sqrt{3} = 5\sqrt{3}\).

• Ignoring Square Roots of Negative Numbers:

  Square roots of negative numbers involve imaginary numbers: \(\sqrt{-1} = i\). Do not attempt to simplify a negative number under a square root without accounting for this.

By being mindful of these common mistakes, you can simplify square roots correctly and avoid errors.

Practicing the simplification of square roots helps reinforce understanding and ensures accuracy. Here are some problems to work through:

1. Simplify \( \sqrt{50} \)

   Solution:

   • Factor 50: \( \sqrt{50} = \sqrt{2 \times 5 \times 5} \)
   • Group the factors: \( \sqrt{50} = \sqrt{5^2 \times 2} \)
   • Take the square root of the perfect square: \( \sqrt{50} = 5\sqrt{2} \)

2. Simplify \( \sqrt{72} \)

   Solution:

   • Factor 72: \( \sqrt{72} = \sqrt{2 \times 2 \times 2 \times 3 \times 3} \)
   • Group the factors: \( \sqrt{72} = \sqrt{2^3 \times 3^2} \)
   • Take the square root of the perfect squares: \( \sqrt{72} = 6\sqrt{2} \)

3. Simplify \( \sqrt{18} \)

   Solution:

   • Factor 18: \( \sqrt{18} = \sqrt{2 \times 3 \times 3} \)
   • Group the factors: \( \sqrt{18} = \sqrt{3^2 \times 2} \)
   • Take the square root of the perfect square: \( \sqrt{18} = 3\sqrt{2} \)

4. Simplify \( \sqrt{45} \)

   Solution:

   • Factor 45: \( \sqrt{45} = \sqrt{3 \times 3 \times 5} \)
   • Group the factors: \( \sqrt{45} = \sqrt{3^2 \times 5} \)
   • Take the square root of the perfect square: \( \sqrt{45} = 3\sqrt{5} \)

5. Simplify \( \sqrt{80} \)

   Solution:

   • Factor 80: \( \sqrt{80} = \sqrt{2 \times 2 \times 2 \times 2 \times 5} \)
   • Group the factors: \( \sqrt{80} = \sqrt{2^4 \times 5} \)
   • Take the square root of the perfect squares: \( \sqrt{80} = 4\sqrt{5} \)

These practice problems cover a range of difficulties and help reinforce the process of breaking down numbers into their prime factors, grouping them, and simplifying the square roots accordingly. Keep practicing to build confidence and proficiency in simplifying square roots!

Simplifying square roots can go beyond basic factorization, incorporating advanced techniques to handle more complex numbers efficiently. Below are several advanced techniques used in simplifying square roots:

1. Using the Conjugate

When dealing with irrational numbers, the conjugate can be used to simplify expressions involving square roots.

• The conjugate of \(a + \sqrt{b}\) is \(a - \sqrt{b}\).
• Multiplying a number by its conjugate helps eliminate the square root, simplifying the expression.

Example:

\[
\frac{5 + \sqrt{3}}{2 + \sqrt{3}} \times \frac{2 - \sqrt{3}}{2 - \sqrt{3}} = \frac{(5 + \sqrt{3})(2 - \sqrt{3})}{(2 + \sqrt{3})(2 - \sqrt{3})}
\]

2. Rationalizing the Denominator

Rationalizing the denominator involves removing square roots from the denominator of a fraction.

• Multiply both numerator and denominator by a suitable conjugate or factor.

Example:

\[
\frac{3}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{3\sqrt{2}}{2}
\]

3. Using Algebraic Identities

Algebraic identities can simplify complex square root expressions.

• For example, \((a+b)^2 = a^2 + 2ab + b^2\) can simplify \(\sqrt{a^2 + 2ab + b^2}\).

Example:

\[
\sqrt{16 + 24\sqrt{2} + 9} = \sqrt{(4 + 3\sqrt{2})^2} = 4 + 3\sqrt{2}
\]

4. Simplifying Nested Radicals

Nesting occurs when a square root is within another square root, which can often be simplified using algebraic methods or specific techniques.

• Identify patterns or use known identities to break down the nested structure.

Example:

\[
\sqrt{7 + 4\sqrt{3}} = \sqrt{(\sqrt{3})^2 + 2\sqrt{3} \cdot 1 + 1^2} = \sqrt{(\sqrt{3} + 1)^2} = \sqrt{3} + 1
\]

5. Prime Factorization Method

This method involves breaking down the number into its prime factors and simplifying from there.

Example:

\[
\sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{(2^2 \times 3^2) \times 2} = 6\sqrt{2}
\]

By mastering these techniques, you can handle a wider range of problems involving square roots with greater confidence and accuracy.

The process of simplifying the square root of 40 demonstrates important principles in mathematics, particularly in understanding radicals and their properties. By breaking down the square root of 40 using methods such as prime factorization and identifying perfect squares, we were able to simplify it to its most reduced form, \(2\sqrt{10}\).

This guide has covered various aspects of simplifying square roots, from basic definitions and methods to advanced techniques. The prime factorization method was crucial in this process, where we identified that 40 can be factored into \(2^3 \times 5\), and from there, simplified to \(2\sqrt{10}\).

Through examples and practice problems, the concepts were reinforced, helping to solidify the understanding of simplifying square roots. The application of these simplified forms in real-life scenarios, such as in geometry and physics, highlights the practical importance of mastering this skill.

In summary, simplifying square roots like that of 40 not only enhances mathematical problem-solving skills but also provides a deeper appreciation of the structure and properties of numbers. It is an essential skill that finds relevance in various fields and everyday situations.