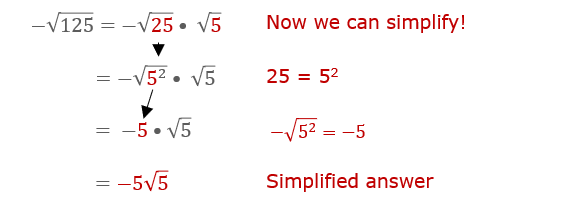Topic square root simplification calculator: Welcome to the Ultimate Square Root Simplification Calculator Guide! This comprehensive guide will walk you through everything you need to know about simplifying square roots, from basic rules to advanced techniques. Whether you're a student or just curious about mathematics, this guide will help you master the art of square root simplification.
Table of Content
- Square Root Simplification Calculator
- Introduction to Square Root Simplification
- Using Square Root Calculators
- Basic Rules for Simplifying Square Roots
- Step-by-Step Simplification Process
- Examples of Simplified Square Roots
- Simplifying Fractions with Square Roots
- Square Roots of Negative Numbers
- Special Cases: Perfect Squares
- Advanced Simplification Techniques
- Square Root Calculator Tools
- Additional Resources and References
- YOUTUBE:
Square Root Simplification Calculator
This tool helps you simplify square roots by breaking down the radicand into its prime factors and extracting perfect squares. It can handle positive, negative, and complex numbers.
Features
- Exact or approximate results
- Handles fractions, decimals, and complex roots
- Step-by-step simplification process
How to Simplify a Square Root
- Factorize the radicand into prime factors.
- Identify and extract perfect squares from the radicand.
- Simplify the remaining radical expression.
Examples
Let's consider a few examples to illustrate the process:
-
Simplify \( \sqrt{8} \):
Factorize: \( \sqrt{8} = \sqrt{4 \times 2} = \sqrt{2^2 \times 2} \)
Extract perfect squares: \( 2\sqrt{2} \)
Result: \( \sqrt{8} = 2\sqrt{2} \approx 2 \times 1.414 = 2.828 \)
-
Simplify \( \sqrt{20} \):
Factorize: \( \sqrt{20} = \sqrt{4 \times 5} = \sqrt{2^2 \times 5} \)
Extract perfect squares: \( 2\sqrt{5} \)
Result: \( \sqrt{20} = 2\sqrt{5} \approx 2 \times 2.236 = 4.472 \)
-
Simplify \( \frac{\sqrt{2}}{\sqrt{3}} \):
Combine radicals: \( \sqrt{\frac{2}{3}} \)
Result: \( \frac{\sqrt{2}}{\sqrt{3}} = \sqrt{\frac{2}{3}} \approx \frac{1.414}{1.732} = 0.816 \)
Properties of Square Roots
| \(\sqrt{a^2} = a\) | \((\sqrt{a})^2 = a\) |
| \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) | \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) |
| \(\sqrt{a^2 \times b} = a \sqrt{b}\) |
Why Simplify Square Roots?
Simplifying square roots is essential in various fields of mathematics, including algebra and geometry. It helps in solving polynomial equations, performing length calculations in geometry, and more. Simplifying expressions to their lowest terms can also make further calculations easier and more accurate.

READ MORE:
Introduction to Square Root Simplification
Square root simplification involves reducing a square root expression to its simplest form. This process makes it easier to understand and work with these expressions. Here are some key points and rules to get started:
- Identify Perfect Squares: Determine if the number under the square root is a perfect square (e.g., 4, 9, 16). If it is, the square root simplifies to a whole number (e.g., √4 = 2).
- Factorization: For non-perfect squares, factorize the number under the square root into its prime factors. This helps in identifying pairs of factors that can be simplified.
- Use Simplification Rules:
- Combine and Simplify: Use the above rules to combine and simplify the factors under the square root.
Let's look at an example:
| Example: | Simplify √50 |
| Step 1: | Factorize 50 into prime factors: 50 = 2 × 5² |
| Step 2: | Rewrite using square root properties: √50 = √(2 × 5²) |
| Step 3: | Simplify: √(2 × 5²) = 5√2 |
| Final Result: | √50 = 5√2 |
By following these steps, you can simplify square roots systematically, making complex expressions more manageable and easier to work with.
Using Square Root Calculators
Square root calculators are essential tools for simplifying radical expressions quickly and accurately. They help in various mathematical computations, particularly in algebra and geometry. Here's a detailed guide on how to use square root calculators:
-
Step 1: Enter the Expression
Input the radical expression you want to simplify. For example, enter
\(\sqrt{50}\) . -
Step 2: Simplify the Expression
The calculator will factorize the number under the root to identify perfect squares. For instance,
\(\sqrt{50}\) can be simplified as\(\sqrt{25 \times 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\) . -
Step 3: Exact and Decimal Form
The calculator provides the result in both exact and decimal forms. For example,
\(\sqrt{50} = 5\sqrt{2} \approx 7.071\) . -
Step 4: Handling Negative Numbers
For negative inputs, the calculator will display complex roots. For example,
\(\sqrt{-4} = 2i\) , wherei is the imaginary unit. -
Step 5: Simplifying Fractions
If the expression involves fractions, the calculator will rationalize the denominator. For instance,
\(\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\) .
Using these steps, you can efficiently simplify any square root expression with a calculator. This process is particularly useful in solving algebraic equations and performing geometric calculations.
Basic Rules for Simplifying Square Roots
Understanding the basic rules for simplifying square roots is essential for solving various mathematical problems. Here are the fundamental principles:
- Product Rule: The square root of a product is the product of the square roots. For any non-negative numbers \(a\) and \(b\), this rule is expressed as:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- Quotient Rule: The square root of a quotient is the quotient of the square roots. For any non-negative numbers \(a\) and \(b\), where \(b \neq 0\), this rule is:
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Simplifying Radicals: To simplify a square root, factor the number into its prime factors and pair them. For example:
- \(\sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}\)
- \(\sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5} = 3\sqrt{5}\)
These rules help in breaking down complex square root expressions into simpler forms, making calculations easier and more intuitive.
Step-by-Step Simplification Process
To simplify a square root, follow these detailed steps:
-
Prime Factorization: Begin by finding the prime factorization of the number under the square root. For example, to simplify \( \sqrt{72} \), first express 72 as a product of prime factors: \( 72 = 2^3 \times 3^2 \).
-
Group the Factors: Group the prime factors in pairs. Each pair of identical factors can be taken out of the square root as a single factor. In our example, \( 72 = 2^3 \times 3^2 \) can be grouped into pairs: \( 72 = (2^2 \times 3^2) \times 2 = (4 \times 9) \times 2 \).
-
Simplify the Expression: Simplify by taking the square root of the perfect squares out of the radical. For \( \sqrt{72} \), it becomes \( \sqrt{4 \times 9 \times 2} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2} \).
-
Combine the Results: Write the simplified form by multiplying the numbers taken out of the radical. Thus, \( \sqrt{72} = 6\sqrt{2} \).
This method ensures the square root is simplified to its most basic form, making calculations easier and more efficient.

Examples of Simplified Square Roots
Understanding the process of simplifying square roots can be greatly enhanced by looking at some specific examples. Here are a few examples that illustrate how to simplify different square root expressions:
-
Example 1: Simplifying \(\sqrt{18}\)
- First, find the prime factors of 18: \(18 = 2 \times 3^2\).
- Next, apply the square root to each factor: \(\sqrt{18} = \sqrt{2 \times 3^2}\).
- Separate the square root of the perfect square: \(\sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3\).
- Therefore, \(\sqrt{18} = 3\sqrt{2}\).
-
Example 2: Simplifying \(\sqrt{50}\)
- Find the prime factors of 50: \(50 = 2 \times 5^2\).
- Apply the square root to each factor: \(\sqrt{50} = \sqrt{2 \times 5^2}\).
- Separate the square root of the perfect square: \(\sqrt{2} \times \sqrt{5^2} = \sqrt{2} \times 5\).
- Thus, \(\sqrt{50} = 5\sqrt{2}\).
-
Example 3: Simplifying \(\sqrt{72}\)
- Find the prime factors of 72: \(72 = 2^3 \times 3^2\).
- Apply the square root to each factor: \(\sqrt{72} = \sqrt{2^3 \times 3^2}\).
- Separate the square root of the perfect square: \(\sqrt{2^3} \times \sqrt{3^2} = \sqrt{8} \times 3\).
- Since \(\sqrt{8} = 2\sqrt{2}\), we have: \(2\sqrt{2} \times 3 = 6\sqrt{2}\).
- Thus, \(\sqrt{72} = 6\sqrt{2}\).
-
Example 4: Simplifying \(\sqrt{98}\)
- Find the prime factors of 98: \(98 = 2 \times 7^2\).
- Apply the square root to each factor: \(\sqrt{98} = \sqrt{2 \times 7^2}\).
- Separate the square root of the perfect square: \(\sqrt{2} \times \sqrt{7^2} = \sqrt{2} \times 7\).
- Therefore, \(\sqrt{98} = 7\sqrt{2}\).
By practicing with these examples, you can develop a deeper understanding of how to simplify square roots and apply these techniques to other similar problems.
Simplifying Fractions with Square Roots
Simplifying fractions that include square roots involves a few systematic steps. By following these steps, you can reduce complex fractions to their simplest forms.
-
Simplify the Square Root:
First, simplify the square root in the fraction. For example, simplify \(\sqrt{72}\) by factoring out the largest perfect square:
\(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\)
-
Rationalize the Denominator:
To eliminate the square root from the denominator, multiply the numerator and the denominator by the conjugate or the same square root term. For instance, to rationalize \(\frac{5}{\sqrt{3}}\), multiply by \(\frac{\sqrt{3}}{\sqrt{3}}\):
\(\frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3}\)
-
Simplify the Fraction:
Combine the results to get the simplified fraction. If the square root can be further simplified, do so.
Examples of Simplifying Fractions with Square Roots
-
Example 1: Simplify \(\frac{\sqrt{18}}{3}\)
\(\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\)
\(\frac{\sqrt{18}}{3} = \frac{3\sqrt{2}}{3} = \sqrt{2}\)
-
Example 2: Simplify \(\frac{2}{\sqrt{12}}\)
\(\sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3}\)
\(\frac{2}{\sqrt{12}} \times \frac{\sqrt{12}}{\sqrt{12}} = \frac{2\sqrt{12}}{12} = \frac{2 \times 2\sqrt{3}}{12} = \frac{4\sqrt{3}}{12} = \frac{\sqrt{3}}{3}\)
-
Example 3: Simplify \(\frac{\sqrt{6}}{\sqrt{2}}\)
\(\frac{\sqrt{6}}{\sqrt{2}} = \sqrt{\frac{6}{2}} = \sqrt{3}\)
By practicing these steps, you can easily simplify fractions containing square roots.
Square Roots of Negative Numbers
Square roots of negative numbers involve the concept of imaginary numbers. When we encounter a negative number under a square root, we use the imaginary unit \(i\), where \(i = \sqrt{-1}\). This allows us to handle the square roots of negative values.
Here's a step-by-step explanation of how to simplify square roots of negative numbers:
Identify the negative number under the square root. For example, consider \(\sqrt{-16}\).
Factor out the \(-1\) from under the square root. This step converts the expression into an imaginary number. So, \(\sqrt{-16}\) becomes \(\sqrt{16 \cdot -1}\).
Apply the property of square roots to separate the factors: \(\sqrt{16 \cdot -1} = \sqrt{16} \cdot \sqrt{-1}\).
Simplify the square root of the positive number and the square root of \(-1\): \(\sqrt{16} = 4\) and \(\sqrt{-1} = i\). Thus, \(\sqrt{16} \cdot \sqrt{-1} = 4i\).
Some examples of simplifying square roots of negative numbers:
\(\sqrt{-4} = \sqrt{4 \cdot -1} = \sqrt{4} \cdot \sqrt{-1} = 2i\)
\(\sqrt{-9} = \sqrt{9 \cdot -1} = \sqrt{9} \cdot \sqrt{-1} = 3i\)
\(\sqrt{-25} = \sqrt{25 \cdot -1} = \sqrt{25} \cdot \sqrt{-1} = 5i\)
In these examples, you can see that each negative number's square root is expressed as a multiple of \(i\). This process allows us to work with square roots of negative numbers using imaginary numbers effectively.
Special Cases: Perfect Squares
Perfect squares are numbers that are the squares of integers. For instance, numbers like 1, 4, 9, 16, and 25 are perfect squares because they can be written as \(1^2\), \(2^2\), \(3^2\), \(4^2\), and \(5^2\), respectively. These special cases are straightforward to simplify since their square roots are always integers.
Identifying Perfect Squares
A perfect square is any number \(x\) where the square root of \(x\) is an integer \(a\) such that \(a^2 = x\). Here are some common perfect squares and their square roots:
- \(1 = 1^2\), so \(\sqrt{1} = 1\)
- \(4 = 2^2\), so \(\sqrt{4} = 2\)
- \(9 = 3^2\), so \(\sqrt{9} = 3\)
- \(16 = 4^2\), so \(\sqrt{16} = 4\)
- \(25 = 5^2\), so \(\sqrt{25} = 5\)
- \(36 = 6^2\), so \(\sqrt{36} = 6\)
- \(49 = 7^2\), so \(\sqrt{49} = 7\)
- \(64 = 8^2\), so \(\sqrt{64} = 8\)
- \(81 = 9^2\), so \(\sqrt{81} = 9\)
- \(100 = 10^2\), so \(\sqrt{100} = 10\)
Why Perfect Squares are Important
Understanding perfect squares is crucial in various mathematical applications, including solving quadratic equations, simplifying radicals, and performing algebraic operations. Recognizing these numbers can significantly speed up calculations and provide insights into more complex mathematical concepts.
Properties of Perfect Squares
- Always non-negative: The square of any real number is always non-negative. Thus, perfect squares are never negative.
- Odd and Even Perfect Squares: The square of an even number is even, and the square of an odd number is odd. For example, \(2^2 = 4\) (even) and \(3^2 = 9\) (odd).
- Sum of Consecutive Odd Numbers: A perfect square can be expressed as the sum of consecutive odd numbers. For instance, \(1 + 3 = 4\), \(1 + 3 + 5 = 9\), \(1 + 3 + 5 + 7 = 16\).
Applications of Perfect Squares
Perfect squares appear frequently in geometry, algebra, and number theory. For example:
- Geometry: The area of a square is a perfect square if the side length is an integer.
- Quadratic Equations: Solving quadratic equations often involves recognizing and working with perfect squares.
- Mathematical Proofs: Many mathematical proofs and theorems involve perfect squares, particularly in number theory.
Conclusion
Perfect squares are fundamental to understanding various mathematical principles. Their simplicity and unique properties make them a vital concept in both basic and advanced mathematics.

Advanced Simplification Techniques
Advanced techniques for simplifying square roots involve using various algebraic properties and rules. These methods are essential for dealing with complex expressions and can simplify calculations significantly. Here are some advanced techniques:
1. Rationalizing the Denominator
When a square root appears in the denominator of a fraction, it is often useful to eliminate it by rationalizing the denominator. This involves multiplying both the numerator and the denominator by the radical in the denominator.
Example:
\[\frac{5}{\sqrt{3}} = \frac{5 \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \frac{5\sqrt{3}}{3}\]
2. Simplifying Products and Quotients of Radicals
The properties of radicals allow us to simplify the product and quotient of square roots.
- Product Rule: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\)
- Quotient Rule: \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\)
Examples:
\(\sqrt{6} \cdot \sqrt{2} = \sqrt{12} = 2\sqrt{3}\)
\(\frac{\sqrt{18}}{\sqrt{2}} = \sqrt{\frac{18}{2}} = \sqrt{9} = 3\)
3. Combining Like Radicals
Like radicals can be combined by adding or subtracting their coefficients, similar to combining like terms in polynomial expressions.
Examples:
- \(3\sqrt{5} + 2\sqrt{5} = (3 + 2)\sqrt{5} = 5\sqrt{5}\)
- \(7\sqrt{3} - 4\sqrt{3} = (7 - 4)\sqrt{3} = 3\sqrt{3}\)
4. Using the Difference of Squares
Square roots can be simplified using the difference of squares formula: \((a + b)(a - b) = a^2 - b^2\).
Example:
\((\sqrt{a} + \sqrt{b})(\sqrt{a} - \sqrt{b}) = (\sqrt{a})^2 - (\sqrt{b})^2 = a - b\)
5. Simplifying Higher-Order Roots
For roots higher than square roots, similar rules apply, but with more complexity. For instance, to simplify \(\sqrt[4]{a^8}\), recognize that \(\sqrt[4]{a^8} = (a^8)^{1/4} = a^{8/4} = a^2\).
6. Simplifying Expressions with Multiple Radicals
When dealing with multiple radicals, it is often useful to use the least common multiple (LCM) to combine them into a single radical for simplification.
Example:
\(\sqrt[4]{64} \cdot \sqrt{6}\) can be simplified by expressing each radical in terms of their prime factors and then combining:
\(\sqrt[4]{2^6} \cdot \sqrt{2 \cdot 3} = 2^{6/4} \cdot \sqrt{6} = 2^{3/2} \cdot \sqrt{6} = 2^{1.5} \cdot \sqrt{6} = 2\sqrt{2} \cdot \sqrt{6} = 2\sqrt{12} = 4\sqrt{3}\)
These techniques, when mastered, can greatly simplify the process of dealing with complex square root expressions and are invaluable tools in advanced mathematics.
Square Root Calculator Tools
Square root calculators are incredibly useful tools for simplifying square roots and performing related calculations. These tools can handle various types of inputs and provide both exact and approximate results. Below are some features and uses of square root calculator tools:
Features of Square Root Calculators
- Simplification to Radical Form: These calculators can reduce square roots to their simplest radical form. For instance, the square root of 50 can be simplified to \( \sqrt{50} = 5\sqrt{2} \).
- Handling Negative Numbers: Some calculators can manage negative inputs and provide complex or imaginary results. For example, \( \sqrt{-9} = 3i \).
- Perfect Square Identification: They can identify if the input is a perfect square and return the corresponding integer. For instance, the square root of 25 is \( \sqrt{25} = 5 \).
- Fractional Inputs: Many calculators support fractional inputs, simplifying expressions like \( \sqrt{\frac{1}{4}} = \frac{1}{2} \).
Using a Square Root Calculator
- Input the Number: Enter the number you want to find the square root of. The calculator will typically provide both exact and decimal approximations.
- Simplify the Result: The calculator will attempt to simplify the square root. For instance, entering 18 will return \( \sqrt{18} = 3\sqrt{2} \).
- Check for Perfect Squares: If the number is a perfect square, the calculator will identify it. For example, entering 36 will return \( \sqrt{36} = 6 \).
- View Decimal Approximations: For non-perfect squares, the calculator will provide a decimal approximation. For example, \( \sqrt{20} \approx 4.472 \).
Examples
| Number | Exact Square Root | Decimal Approximation |
|---|---|---|
| 16 | 4 | 4.000 |
| 20 | \( 2\sqrt{5} \) | 4.472 |
| 50 | \( 5\sqrt{2} \) | 7.071 |
| 100 | 10 | 10.000 |
By using these tools, you can quickly and accurately simplify square roots, solve radical equations, and explore the properties of square roots in both their exact and approximate forms.
Additional Resources and References
For further exploration and deeper understanding of square root simplification and related concepts, consider the following resources and tools:
- CalculatorSoup - Provides an online that can handle both positive and negative real numbers, as well as determine if the input is a perfect square.
- Mathway - Offers a comprehensive that delivers exact and decimal forms of square roots, with step-by-step solutions.
- MathCracker - Features a that simplifies radical expressions using basic algebraic rules and principles.
- Omni Calculator - A versatile tool for simplifying radicals, available at , which provides step-by-step explanations and handles complex radical expressions.
In addition to these tools, the following educational websites offer valuable information on square root simplification:
- - A user-friendly platform with comprehensive lessons on square roots and their properties.
- - Offers free courses and practice exercises on radicals and square roots, including video tutorials.
- - Provides detailed explanations and examples of simplifying radicals, tailored for different learning levels.
These resources should equip you with the necessary tools and knowledge to master square root simplification. Happy learning!
Hướng dẫn Sử dụng Máy tính ClassWiz - Đại số 4-1 Đơn giản hóa Căn thức
READ MORE:
Đơn giản hóa căn bậc hai với máy tính đồ thị