Topic simplify 45 square root: Unlock the secrets of simplifying the square root of 45 with our comprehensive guide. Learn the straightforward steps to break down 45 into prime factors and simplify its square root. Perfect for students and math enthusiasts, this article will enhance your understanding and improve your mathematical skills. Dive in and master the concept today!
Table of Content
- Simplifying the Square Root of 45
- Introduction to Square Roots
- Understanding the Square Root of 45
- Prime Factorization of 45
- Steps to Simplify the Square Root of 45
- Using Properties of Square Roots
- Simplification of √45
- Examples of Simplifying Other Square Roots
- Applications of Simplified Square Roots
- Common Mistakes to Avoid
- Practice Problems and Solutions
- Conclusion
- Additional Resources
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai của 45, giúp bạn nắm vững kiến thức toán học một cách dễ hiểu.
Simplifying the Square Root of 45
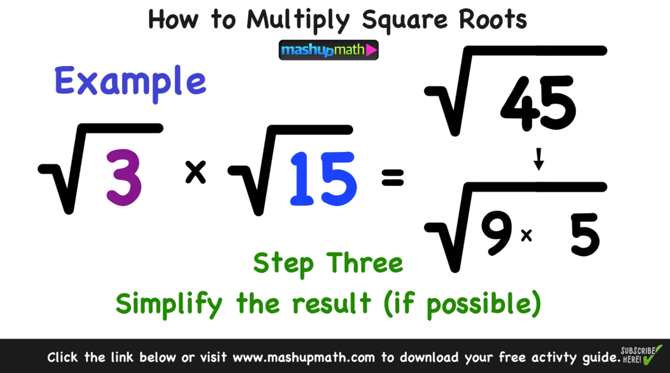
The square root of 45 can be simplified by factoring the number into its prime factors.
Steps to Simplify √45:
- Factor 45 into its prime factors: 45 = 32 × 5.
- Use the property of square roots that √(a × b) = √a × √b.
- Simplify the square root of the perfect square: √(32 × 5) = √32 × √5.
- Since √32 = 3, we get: 3√5.
Therefore, the simplified form of √45 is:
This simplification is useful in various mathematical contexts, making calculations more straightforward and elegant.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 × 3 = 9.
Square roots are denoted using the radical symbol √. For instance, √9 represents the square root of 9.
Understanding square roots involves several key aspects:
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because they are the squares of whole numbers.
- Non-Perfect Squares: Numbers that are not perfect squares, like 2, 3, 5, and 45, have square roots that are irrational numbers.
- Properties of Square Roots: Key properties include:
- √(a × b) = √a × √b
- √(a/b) = √a / √b
- (√a)2 = a
To simplify the square root of a number, you often need to factor the number into its prime factors and apply these properties. This makes calculations easier and helps in understanding the relationships between different numbers.
In this guide, we will focus on simplifying the square root of 45, demonstrating the step-by-step process and providing additional insights into the world of square roots.
Understanding the Square Root of 45
The square root of 45 can be simplified by expressing it in its simplest radical form. This involves breaking down the number into its prime factors and using the properties of square roots.
- First, identify the factors of 45: 1, 3, 5, 9, 15, 45.
- Next, find the perfect squares from these factors: 1, 9.
- Divide 45 by the largest perfect square: 45 / 9 = 5.
- Calculate the square root of the largest perfect square: √9 = 3.
- Combine these results: 3√5.
Thus, the simplified form of √45 is 3√5. This method uses the fundamental property of square roots that √ab = √a * √b to break down the original number into a simpler form.
By following these steps, we achieve a simplified radical expression that is easier to work with in various mathematical contexts.
Prime Factorization of 45
Prime factorization is the process of breaking down a number into its basic prime numbers. For the number 45, we can follow these steps:
- Start by dividing 45 by the smallest prime number, which is 2. Since 45 is odd, it is not divisible by 2.
- Next, try dividing by the next smallest prime number, 3. Since 45 is divisible by 3 (45 ÷ 3 = 15), we write:
45 = 3 × 15 - Continue factoring 15 by the smallest prime number, which is 3. Since 15 is divisible by 3 (15 ÷ 3 = 5), we write:
15 = 3 × 5 - Now, 5 is a prime number, so we cannot factor it further.
Combining all the factors, we get:
45 = 3 × 3 × 5 or 45 = 32 × 5
Thus, the prime factorization of 45 is 32 × 5.
| Step | Explanation |
|---|---|
| 1 | Start with the number 45. |
| 2 | Divide by the smallest prime number (3): 45 ÷ 3 = 15. |
| 3 | Continue dividing by 3: 15 ÷ 3 = 5. |
| 4 | Since 5 is a prime number, we stop here. |
The final prime factorization is: 45 = 32 × 5.
Steps to Simplify the Square Root of 45
To simplify the square root of 45, follow these detailed steps:
- Prime Factorization:
- Begin by expressing 45 as a product of its prime factors.
- 45 can be written as \( 9 \times 5 \).
- Next, factor 9 into \( 3^2 \), so 45 becomes \( 3^2 \times 5 \).
- Applying the Square Root Property:
- Use the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Rewrite \( \sqrt{45} \) as \( \sqrt{3^2 \times 5} \).
- Separate the square root into two parts: \( \sqrt{3^2} \times \sqrt{5} \).
- Simplify:
- The square root of \( 3^2 \) is 3, so \( \sqrt{3^2} = 3 \).
- Therefore, \( \sqrt{45} = 3 \times \sqrt{5} \).
Thus, the simplified form of \( \sqrt{45} \) is \( 3\sqrt{5} \).

Using Properties of Square Roots
When simplifying square roots, certain properties can be very useful. Here are some key properties and steps to use them effectively:
- Product Property: For any non-negative numbers \(a\) and \(b\), the square root of their product is the product of their square roots:
\[
\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}
\]
Example: To simplify \(\sqrt{45}\), we use the product property by expressing 45 as a product of its factors:
\(\sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5}\)
Since \(\sqrt{9} = 3\), we get:
\(\sqrt{45} = 3\sqrt{5}\)
- Quotient Property: For any non-negative numbers \(a\) and \(b\) (where \(b \neq 0\)), the square root of their quotient is the quotient of their square roots:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
Example: To simplify \(\sqrt{\frac{45}{5}}\), we use the quotient property:
\(\sqrt{\frac{45}{5}} = \frac{\sqrt{45}}{\sqrt{5}}\)
Using the product property and knowing that \(\sqrt{45} = 3\sqrt{5}\), we have:
\(\frac{3\sqrt{5}}{\sqrt{5}} = 3\)
By using these properties, we can simplify many square roots effectively. Practicing these techniques helps in recognizing patterns and simplifying complex expressions more quickly.
Simplification of √45
To simplify √45, we start by determining its prime factors.
The prime factorization of 45 is:
45 = 3 × 3 × 5
Using the property of square roots that allows us to separate the square root of a product into the product of square roots of each factor, we get:
√45 = √(3 × 3 × 5)
√45 = √(32 × 5)
√45 = 3√5
Therefore, the simplified form of √45 is 3√5.
Examples of Simplifying Other Square Roots
In this section, we'll explore various examples of simplifying square roots, providing a step-by-step approach to understanding the process. Simplifying square roots involves breaking down the radicand (the number inside the square root) into its prime factors and then simplifying the expression. Here are some examples:
Example 1: Simplifying √50
To simplify √50, we follow these steps:
- Find the prime factorization of 50: 50 = 2 × 5 × 5.
- Pair the prime factors: 50 = 2 × (52).
- Take the square root of each pair of factors: √50 = √(2 × 52) = 5√2.
Thus, √50 simplifies to 5√2.
Example 2: Simplifying √72
To simplify √72, follow these steps:
- Find the prime factorization of 72: 72 = 2 × 2 × 2 × 3 × 3.
- Pair the prime factors: 72 = (23 × 32).
- Take the square root of each pair of factors: √72 = √(23 × 32) = 3√(23) = 3√8 = 3 × 2√2 = 6√2.
Thus, √72 simplifies to 6√2.
Example 3: Simplifying √18
To simplify √18, follow these steps:
- Find the prime factorization of 18: 18 = 2 × 3 × 3.
- Pair the prime factors: 18 = 2 × (32).
- Take the square root of each pair of factors: √18 = √(2 × 32) = 3√2.
Thus, √18 simplifies to 3√2.
Example 4: Simplifying √200
To simplify √200, follow these steps:
- Find the prime factorization of 200: 200 = 2 × 2 × 2 × 5 × 5.
- Pair the prime factors: 200 = (23 × 52).
- Take the square root of each pair of factors: √200 = √(23 × 52) = 5√(23) = 5√8 = 5 × 2√2 = 10√2.
Thus, √200 simplifies to 10√2.
Example 5: Simplifying √32
To simplify √32, follow these steps:
- Find the prime factorization of 32: 32 = 2 × 2 × 2 × 2 × 2.
- Pair the prime factors: 32 = 25.
- Take the square root of each pair of factors: √32 = √(25) = 2√(23) = 2√8 = 2 × 2√2 = 4√2.
Thus, √32 simplifies to 4√2.
Applications of Simplified Square Roots
Simplified square roots have numerous applications in various fields. Here are some key examples:
-
Geometry and Measurement:
Square roots are essential in geometry, especially when dealing with the area of squares and other geometric shapes. For instance, if you know the area of a square, you can find the side length by taking the square root of the area. This is useful in real-world scenarios such as finding the dimensions of a garden, a room, or any square-shaped object. For example, if the area of a lawn is 225 square feet, the length of each side is \( \sqrt{225} = 15 \) feet.
-
Physics and Engineering:
In physics, square roots are used in formulas that describe natural phenomena. One common application is calculating the time it takes for an object to fall to the ground due to gravity. The formula is \( t = \frac{\sqrt{h}}{4} \), where \( h \) is the height in feet. For example, if an object is dropped from 64 feet, the time it takes to reach the ground is \( \frac{\sqrt{64}}{4} = 2 \) seconds.
-
Accident Investigation:
Law enforcement uses square roots to determine the speed of vehicles involved in accidents. By measuring the length of skid marks, they can estimate the speed of a vehicle before braking using the formula \( \text{speed} = \sqrt{24 \times d} \), where \( d \) is the skid mark length in feet. For instance, if the skid marks are 190 feet long, the estimated speed is \( \sqrt{24 \times 190} \approx 67.5 \) miles per hour.
-
Construction and Architecture:
Square roots help in calculating dimensions and ensuring structures are properly proportioned. For example, if a construction plan specifies a diagonal measurement of 50 feet for a square plot, the side length of the plot is \( \frac{50}{\sqrt{2}} \approx 35.4 \) feet, ensuring accurate layout and measurements.
-
Finance:
In finance, square roots are used to calculate volatility and standard deviation in investment portfolios. These metrics help investors understand the risk and variation in asset returns, aiding in better investment decisions.
Common Mistakes to Avoid
When simplifying square roots, there are several common mistakes that can lead to incorrect results. Being aware of these can help improve your accuracy:
-
Ignoring Prime Factorization:
One of the most common mistakes is not breaking down the number into its prime factors. For example, with √45, you must recognize that 45 = 3 × 3 × 5, allowing you to simplify √45 as 3√5.
-
Incorrect Pairing of Factors:
When simplifying, it's crucial to correctly pair factors under the square root. Missing a pair or incorrectly grouping numbers can lead to errors. For example, if you miss that 9 is a perfect square in √45, you may not simplify it correctly.
-
Not Using Perfect Squares:
Failing to identify and use perfect squares can complicate simplification. Recognizing that 9 is a perfect square in √45 helps to simplify the expression to 3√5.
-
Incorrect Application of Square Root Properties:
Misapplying properties such as the product and quotient rules for square roots can result in mistakes. For instance, √(a×b) = √a × √b should be used properly to avoid incorrect simplifications.
-
Leaving Radicals in Denominators:
In many cases, it's important to rationalize the denominator. For instance, instead of leaving an expression as 1/√2, it should be simplified to √2/2.
By avoiding these common mistakes and carefully applying the principles of simplification, you can achieve accurate results when working with square roots.
Practice Problems and Solutions
Below are some practice problems to help you master the simplification of square roots. Each problem is followed by a detailed solution to guide you through the process.
-
Simplify \( \sqrt{18} \)
Solution:
- Step 1: Factorize 18 into prime factors: \( 18 = 2 \times 3^2 \)
- Step 2: Rewrite the square root using the prime factors: \( \sqrt{18} = \sqrt{2 \times 3^2} \)
- Step 3: Simplify by taking the square root of the perfect square: \( \sqrt{2 \times 3^2} = 3\sqrt{2} \)
Final Answer: \( 3\sqrt{2} \)
-
Simplify \( \sqrt{50} \)
Solution:
- Step 1: Factorize 50 into prime factors: \( 50 = 2 \times 5^2 \)
- Step 2: Rewrite the square root using the prime factors: \( \sqrt{50} = \sqrt{2 \times 5^2} \)
- Step 3: Simplify by taking the square root of the perfect square: \( \sqrt{2 \times 5^2} = 5\sqrt{2} \)
Final Answer: \( 5\sqrt{2} \)
-
Simplify \( \sqrt{72} \)
Solution:
- Step 1: Factorize 72 into prime factors: \( 72 = 2^3 \times 3^2 \)
- Step 2: Rewrite the square root using the prime factors: \( \sqrt{72} = \sqrt{2^3 \times 3^2} \)
- Step 3: Simplify by taking the square root of the perfect squares: \( \sqrt{2^3 \times 3^2} = 3\sqrt{8} = 3 \times 2\sqrt{2} = 6\sqrt{2} \)
Final Answer: \( 6\sqrt{2} \)
-
Simplify \( \sqrt{98} \)
Solution:
- Step 1: Factorize 98 into prime factors: \( 98 = 2 \times 7^2 \)
- Step 2: Rewrite the square root using the prime factors: \( \sqrt{98} = \sqrt{2 \times 7^2} \)
- Step 3: Simplify by taking the square root of the perfect square: \( \sqrt{2 \times 7^2} = 7\sqrt{2} \)
Final Answer: \( 7\sqrt{2} \)
-
Simplify \( \sqrt{200} \)
Solution:
- Step 1: Factorize 200 into prime factors: \( 200 = 2^3 \times 5^2 \)
- Step 2: Rewrite the square root using the prime factors: \( \sqrt{200} = \sqrt{2^3 \times 5^2} \)
- Step 3: Simplify by taking the square root of the perfect squares: \( \sqrt{2^3 \times 5^2} = 5\sqrt{8} = 5 \times 2\sqrt{2} = 10\sqrt{2} \)
Final Answer: \( 10\sqrt{2} \)
Conclusion
Simplifying square roots is a fundamental mathematical skill that has numerous practical applications. Throughout this guide, we've explored the steps to simplify the square root of 45, along with various examples and common pitfalls. Understanding these concepts allows for greater accuracy and efficiency in both academic and real-world scenarios.
By breaking down the process into manageable steps, we demonstrated how to factorize 45 into its prime components and simplify it as \( 3 \sqrt{5} \). This method can be applied to other non-perfect squares, aiding in the simplification of more complex expressions.
Moreover, recognizing the properties of square roots and avoiding common mistakes ensures that your calculations are correct and reliable. Simplified square roots are not only easier to work with but also essential in various fields such as engineering, physics, and computer science.
Ultimately, mastering the simplification of square roots enhances your mathematical toolkit, preparing you for more advanced topics and practical problem-solving. We encourage you to continue practicing with different numbers to solidify your understanding and confidence in this essential skill.
Thank you for following along in this comprehensive guide on simplifying square roots. We hope you find these techniques useful and applicable in your mathematical journey.
Additional Resources
To further your understanding of simplifying square roots, especially \(\sqrt{45}\), here are some additional resources that can provide more in-depth explanations, examples, and practice problems:
- - This page offers step-by-step solutions and explanations for simplifying the square root of 45 and similar problems.
- - Use Symbolab to practice simplifying square roots and explore various algebraic problems with detailed solutions.
- - A series of videos and exercises on Khan Academy that cover simplifying square roots, including practical applications and deeper theoretical insights.
- - This video provides a comprehensive explanation of the process of simplifying square roots with worked examples.
- - A detailed tutorial on simplifying radical expressions, including square roots, with practice problems and solutions.
- - An easy-to-understand guide to simplifying square roots with interactive examples and exercises.
These resources should help you gain a deeper understanding and provide ample practice opportunities to master the concept of simplifying square roots.

Video hướng dẫn cách đơn giản hóa căn bậc hai của 45, giúp bạn nắm vững kiến thức toán học một cách dễ hiểu.
Cách Đơn Giản Hóa Căn Bậc Hai Của 45: sqrt(45)
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai của 45, giúp bạn hiểu rõ hơn về cách tính toán toán học một cách dễ dàng.
Cách Đơn Giản Hóa Căn Bậc Hai Của 45












