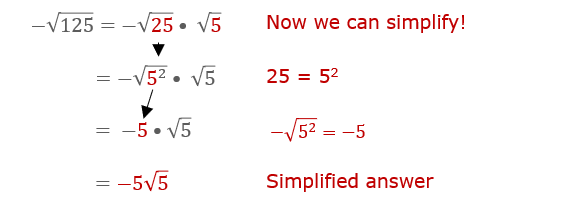Topic simplified square root calculator: Discover the ultimate guide to using a simplified square root calculator. Learn how to effortlessly simplify square roots, understand perfect squares, and apply properties of square roots to solve mathematical problems efficiently. Enhance your math skills with practical examples and step-by-step instructions for accurate and simplified calculations.
Table of Content
- Square Root Calculator
- Introduction to Simplified Square Root Calculators
- How to Use a Square Root Calculator
- Step-by-Step Guide to Simplifying Square Roots
- Understanding Perfect Squares and Factors
- Examples of Simplifying Square Roots
- Multiplying and Dividing Square Roots
- Simplifying Square Roots in Fractions
- Practical Applications of Square Roots
- Common Mistakes and How to Avoid Them
- Advanced Techniques for Simplifying Square Roots
- Using Technology to Simplify Square Roots
- Frequently Asked Questions
- Conclusion
- YOUTUBE:
Square Root Calculator
This square root calculator is designed to simplify square roots to their simplest radical form and also provide an approximation. It is a useful tool for both educational and practical applications, making it easier to handle square roots in various mathematical contexts.
How to Simplify Square Roots
To simplify a square root, follow these steps:
- Identify the factors of the number under the square root symbol.
- Check if any of these factors are perfect squares (e.g., 4, 9, 16, 25, etc.).
- If a perfect square is found, express the original number as a product of this perfect square and another number.
- Apply the property: \( \sqrt{x \cdot y} = \sqrt{x} \cdot \sqrt{y} \) to separate the square root into simpler parts.
- Simplify further if possible.
For example:
- To simplify \( \sqrt{27} \):
- Factors of 27 are 1, 3, 9, 27. Since 9 is a perfect square:
- \( \sqrt{27} = \sqrt{9 \cdot 3} = \sqrt{9} \cdot \sqrt{3} = 3\sqrt{3} \)
Additional Examples
- \( \sqrt{8} = \sqrt{4 \cdot 2} = \sqrt{4} \cdot \sqrt{2} = 2\sqrt{2} \)
- \( \sqrt{144} = \sqrt{12 \cdot 12} = 12 \) (since 144 is a perfect square)
Properties of Square Roots
| \( \sqrt{a^2} = a \) | For any positive real number \( a \) |
| \( (\sqrt{a})^2 = a \) | For any number \( a \) |
| \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) | For any numbers \( a \) and \( b \) |
| \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) | For any numbers \( a \) and \( b \) |
Adding and Subtracting Square Roots
Adding or subtracting square roots requires that the radicands (the numbers under the square root symbol) be the same. For example:
- \( \sqrt{2} + \sqrt{3} \neq \sqrt{5} \)
- \( \sqrt{2} + \sqrt{2} = 2\sqrt{2} \)
Square Root Calculator Usage
To use the calculator, simply enter a positive or negative number into the input field. The calculator will reduce the square root to its simplest radical form and also provide a decimal approximation if necessary. This is useful for both exact calculations and practical estimations.
Start simplifying your square roots and enhance your mathematical problem-solving skills with our efficient square root calculator!

READ MORE:
Introduction to Simplified Square Root Calculators
A simplified square root calculator is a tool designed to help users easily find the square root of a given number and simplify it if possible. These calculators are particularly useful for students and professionals who need to perform mathematical calculations quickly and accurately.
Simplifying square roots involves breaking down the number under the square root sign into its prime factors and then simplifying it using the properties of square roots. For instance, the square root of 45 can be simplified by recognizing that 45 = 9 x 5, thus √45 = √(9 x 5) = √9 x √5 = 3√5.
These calculators typically allow users to input any number, and the tool will automatically determine if the number can be simplified. If it can, the calculator will provide both the simplified radical form and the decimal form.
The primary benefits of using a simplified square root calculator include:
- Quickly finding the square root of both perfect and non-perfect squares.
- Understanding the step-by-step process of simplifying square roots.
- Performing additional operations such as adding, subtracting, multiplying, and dividing square roots.
- Handling more complex numbers, including those with higher-order roots and complex numbers.
Overall, a simplified square root calculator is an essential tool for anyone dealing with mathematical problems involving square roots, providing a fast and efficient way to simplify and calculate roots accurately.
How to Use a Square Root Calculator
Using a square root calculator is a straightforward process that allows you to find the square root of any number quickly. Here are the steps to follow:
- Open the square root calculator on your chosen platform.
- Enter the number you want to find the square root for into the input field.
- Click on the "Calculate" button to process the input.
- The calculator will display the square root of the entered number, both in its simplest radical form and as a decimal approximation.
Some calculators, like the one provided by Mathway, will give you the result in exact form if the number is a perfect square, and both exact and decimal forms if it is not a perfect square.
Additionally, calculators such as those on MathGoodies and BYJU's provide user-friendly interfaces with options to clear the input and start over if needed. This ensures accuracy and ease of use, especially for students and educators who frequently work with square roots.
These tools are designed to handle both simple and complex square root calculations, making them essential for anyone dealing with mathematics.
Step-by-Step Guide to Simplifying Square Roots
Simplifying square roots involves breaking down a number into its prime factors and pairing them to find perfect squares. Here is a step-by-step guide to help you through the process:
-
Identify the factors of the number. Break down the number into its prime factors.
For example, to simplify \( \sqrt{72} \):
\( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
-
Pair the prime factors. Group the factors into pairs of identical numbers.
In our example: \( 72 = (2 \times 2) \times (3 \times 3) \times 2 \)
-
Take the square root of each pair. Each pair of identical numbers can be taken out of the square root as a single number.
\( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} \)
-
Simplify the expression. Multiply the numbers outside the square root and leave the remaining factors inside the square root.
So, \( \sqrt{72} = 6\sqrt{2} \)
By following these steps, you can simplify any square root to its simplest radical form. This method helps in making calculations easier and more understandable.
Understanding Perfect Squares and Factors
Perfect squares and factors are essential concepts in simplifying square roots. Understanding these terms and their properties will help you work more effectively with square roots.
What is a Perfect Square?
A perfect square is a number that can be expressed as the product of an integer with itself. For example, the numbers 1, 4, 9, 16, and 25 are perfect squares because they are the squares of 1, 2, 3, 4, and 5, respectively. Mathematically, a number n is a perfect square if there exists an integer a such that n = a^2.
Examples of Perfect Squares
- \(1 = 1^2\)
- \(4 = 2^2\)
- \(9 = 3^2\)
- \(16 = 4^2\)
- \(25 = 5^2\)
- \(36 = 6^2\)
- \(49 = 7^2\)
- \(64 = 8^2\)
- \(81 = 9^2\)
- \(100 = 10^2\)
Prime Factorization
Prime factorization involves breaking down a number into its prime factors. This method is useful for simplifying square roots. To find the prime factorization of a number:
- Divide the number by the smallest prime number (2, 3, 5, 7, etc.).
- Continue dividing the quotient by the smallest prime number until you reach 1.
- The prime factors are the prime numbers you used to divide.
For example, the prime factorization of 144 is \(2^4 \times 3^2\). This means:
- \(144 \div 2 = 72\)
- \(72 \div 2 = 36\)
- \(36 \div 2 = 18\)
- \(18 \div 2 = 9\)
- \(9 \div 3 = 3\)
- \(3 \div 3 = 1\)
Finding Perfect Square Factors
To simplify a square root, identify the perfect square factors of the radicand (the number under the square root symbol). For instance, consider the square root of 72:
- Prime factorize 72: \(72 = 2^3 \times 3^2\)
- Identify pairs of prime factors: \(2^3\) contains one pair of 2's and one single 2, \(3^2\) contains one pair of 3's.
- Take one number from each pair outside the square root: \(\sqrt{72} = \sqrt{(2^2 \times 3^2) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
Steps to Simplify Square Roots
- Prime factorize the radicand.
- Group the prime factors into pairs.
- Move one factor from each pair outside the square root.
- Multiply the factors outside the square root.
- Leave any unpaired factors inside the square root.
Following these steps ensures that you simplify square roots correctly, making calculations easier and more accurate.

Examples of Simplifying Square Roots
Understanding how to simplify square roots can be greatly aided by working through several examples. Here, we will go through a few examples step-by-step to demonstrate the process.
Example 1: Simplifying \( \sqrt{27} \)
- Identify the factors of 27 that are perfect squares.
\( 27 = 9 \times 3 \)
- Express the square root as a product of square roots.
\( \sqrt{27} = \sqrt{9 \times 3} \)
- Simplify by taking the square root of the perfect square.
\( \sqrt{9 \times 3} = \sqrt{9} \times \sqrt{3} = 3\sqrt{3} \)
Example 2: Simplifying \( \sqrt{45} \)
- Identify the factors of 45 that are perfect squares.
\( 45 = 9 \times 5 \)
- Express the square root as a product of square roots.
\( \sqrt{45} = \sqrt{9 \times 5} \)
- Simplify by taking the square root of the perfect square.
\( \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \)
Example 3: Simplifying \( \sqrt{72} \)
- Identify the factors of 72 that are perfect squares.
\( 72 = 36 \times 2 \)
- Express the square root as a product of square roots.
\( \sqrt{72} = \sqrt{36 \times 2} \)
- Simplify by taking the square root of the perfect square.
\( \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2} \)
Example 4: Simplifying \( \sqrt{50} \)
- Identify the factors of 50 that are perfect squares.
\( 50 = 25 \times 2 \)
- Express the square root as a product of square roots.
\( \sqrt{50} = \sqrt{25 \times 2} \)
- Simplify by taking the square root of the perfect square.
\( \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \)
Example 5: Simplifying \( \sqrt{12} \)
- Identify the factors of 12 that are perfect squares.
\( 12 = 4 \times 3 \)
- Express the square root as a product of square roots.
\( \sqrt{12} = \sqrt{4 \times 3} \)
- Simplify by taking the square root of the perfect square.
\( \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \)
By practicing these examples, you'll become more comfortable with the process of simplifying square roots. Always remember to look for the largest perfect square factor to simplify the process.
Multiplying and Dividing Square Roots
Multiplying and dividing square roots involves operations that require careful consideration of the properties of radicals. Here’s how to approach these operations:
- Multiplication: To multiply square roots, multiply the numbers outside the radicals (coefficients) and multiply the numbers inside the radicals (radicands). For example, \( \sqrt{2} \times \sqrt{3} = \sqrt{6} \).
- Division: When dividing square roots, divide the numbers outside the radicals and divide the numbers inside the radicals. If the radicand of the divisor is a perfect square, simplify the division by rationalizing the denominator. For example, \( \frac{\sqrt{8}}{\sqrt{2}} = \sqrt{\frac{8}{2}} = \sqrt{4} = 2 \).
- Properties: Remember properties such as \( \sqrt{a} \times \sqrt{b} = \sqrt{ab} \) and \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \) when simplifying expressions involving multiple square roots.
- Simplification: Always simplify the resulting expression by factoring out any perfect squares from the radicand.
- Applications: These operations are fundamental in algebra, geometry, and calculus for solving equations and simplifying complex expressions involving square roots.
Simplifying Square Roots in Fractions
Simplifying square roots in fractions involves handling radicals within numerator and denominator. Here’s how to simplify such expressions:
- Rationalizing the Denominator: If the denominator contains a square root, multiply both numerator and denominator by the conjugate of the denominator to eliminate the radical in the denominator. For example, \( \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \).
- Combining Like Terms: Simplify the expression by combining and rationalizing terms whenever possible, ensuring the final fraction is in its simplest form.
- Applications: Understanding how to simplify square roots in fractions is crucial for solving equations in algebra, trigonometry, and calculus, where such forms frequently appear.
Practical Applications of Square Roots
Square roots have numerous practical applications across various fields. Here are some notable examples:
- Engineering: Calculating the magnitude of alternating current (AC) or alternating voltage (AC) in electrical engineering.
- Physics: Determining distances in geometric optics, such as focal lengths of lenses and mirrors.
- Finance: Estimating the standard deviation in statistical analysis and risk assessment.
- Geometry: Finding the lengths of sides of right triangles and other geometric figures.
- Computer Graphics: Calculating distances and coordinates in three-dimensional space for rendering.
- Navigation: Determining distances and locations using GPS systems and satellite positioning.
- Medicine: Assessing body mass index (BMI) and dosage calculations based on body weight.
- Astronomy: Measuring distances between stars and galaxies using the brightness and luminosity data.
Understanding and applying square roots enhances problem-solving skills and facilitates accurate calculations in various real-world scenarios.

Common Mistakes and How to Avoid Them
When dealing with square roots, it's easy to fall into common pitfalls. Here’s how to avoid them:
- Mixing Up Operations: Ensure you apply the correct operation (addition, subtraction, multiplication, division) to square roots and their coefficients.
- Forgetting Simplification: Always simplify square root expressions by factoring out any perfect squares from the radicand.
- Incorrect Use of Properties: Understand and apply properties of square roots correctly, such as \( \sqrt{a} \times \sqrt{b} = \sqrt{ab} \) and \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \).
- Rationalizing Improperly: When rationalizing denominators, ensure you multiply by the conjugate to eliminate the square root properly.
- Not Checking Answers: Always double-check your calculations, especially when dealing with complex expressions involving square roots.
By being aware of these common mistakes and following these guidelines, you can improve your proficiency in working with square roots and avoid errors in mathematical computations.
Advanced Techniques for Simplifying Square Roots
Mastering advanced techniques for simplifying square roots involves deeper understanding and practice. Here are some advanced methods:
- Factoring: Factor the radicand into its prime factors to simplify square roots.
- Using Perfect Squares: Utilize perfect square factors within the radicand to simplify expressions.
- Conjugate Method: For rationalizing denominators with square roots, multiply by the conjugate of the denominator to eliminate radicals.
- Binomial Expansion: Apply binomial expansion techniques to simplify complex square root expressions.
- Variable Substitution: Substitute variables to transform square root expressions into simpler forms, facilitating easier manipulation.
- Exponent Rules: Apply exponent rules to simplify square root expressions involving powers and radicals.
These advanced techniques are essential for tackling higher-level algebraic problems and ensuring accurate and efficient calculations involving square roots.
Using Technology to Simplify Square Roots
Technology offers efficient methods for simplifying square roots. Here’s how:
- Calculator Applications: Utilize online or handheld calculators capable of directly computing and simplifying square roots.
- Software Tools: Use mathematical software like Mathematica, MATLAB, or Wolfram Alpha to handle complex square root expressions.
- Graphing Calculators: Graphing calculators allow for visualization of square root functions and precise calculations.
- Online Resources: Access web-based tools and calculators that provide step-by-step solutions and explanations for simplifying square roots.
- Mobile Apps: Install educational apps on smartphones and tablets that include square root simplification as part of their functionality.
By leveraging technological resources, individuals can streamline the process of simplifying square roots and focus on understanding the underlying concepts of mathematics.
Frequently Asked Questions
-
What is a square root?
A square root of a number \( a \) is a value \( x \) such that \( x^2 = a \).
-
How do you simplify square roots?
To simplify a square root, factor the radicand into its prime factors and remove any perfect square factors from under the radical.
-
What are perfect squares?
Perfect squares are numbers that result from squaring integers, such as 1, 4, 9, 16, etc.
-
Can you add or subtract square roots?
Yes, you can add or subtract square roots if they have the same radicand (number under the square root symbol).
-
How do you multiply or divide square roots?
To multiply square roots, multiply the numbers outside and inside the radicals. To divide, divide the numbers outside and inside the radicals, and rationalize the denominator if necessary.
-
What are some practical applications of square roots?
Square roots are used in fields such as engineering, physics, finance, geometry, computer graphics, navigation, medicine, and astronomy.
-
How can technology help in simplifying square roots?
Technology aids in simplifying square roots through calculators, software tools, graphing calculators, online resources, and mobile apps designed for mathematical computations.

Conclusion
In conclusion, a simplified square root calculator is an invaluable tool for students, educators, and anyone working with mathematics. By breaking down complex square root expressions into simpler forms, these calculators help make mathematical computations more accessible and understandable. Utilizing such calculators can significantly enhance one's understanding of mathematical principles and improve problem-solving skills.
The journey of simplifying square roots involves recognizing perfect squares within the radicand, applying mathematical properties, and using rules that govern the manipulation of radicals. With practice, one can become proficient in simplifying even the most complicated square root expressions.
Additionally, modern technology has made these calculators easily accessible online, providing step-by-step solutions and explanations that further aid in learning. Whether you're working on basic arithmetic or tackling more advanced algebraic problems, a simplified square root calculator can be a powerful aid in your mathematical toolkit.
As you continue to explore the world of mathematics, remember that tools like these are designed to support your learning and help you achieve greater accuracy and efficiency in your calculations. Embrace the technology available to you, and enjoy the process of uncovering the beauty and logic of mathematical concepts.
Hướng Dẫn Sử Dụng Máy Tính ClassWiz - Đại Số 4-1 Đơn Giản Hoá Căn Thức
READ MORE:
Đơn Giản Hoá Căn Thức Bằng Máy Tính Đồ Thị