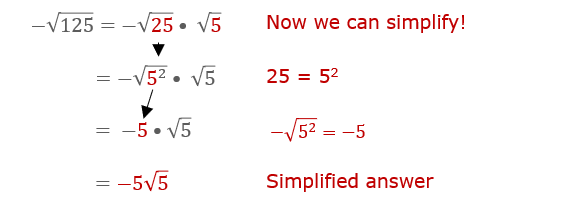How to Simplify Fractions with Square Roots in the Denominator

When simplifying fractions that have square roots in the denominator, the goal is to eliminate the square root from the denominator. This process is known as "rationalizing the denominator." Below is a step-by-step guide on how to do this:

Step-by-Step Guide

1. Identify the fraction you want to simplify. For example, consider the fraction:

   \[ \frac{1}{\sqrt{a}} \]

2. Multiply both the numerator and the denominator by the square root in the denominator. This is to make the denominator a rational number. For our example:

   \[ \frac{1 \cdot \sqrt{a}}{\sqrt{a} \cdot \sqrt{a}} = \frac{\sqrt{a}}{a} \]

3. Simplify the resulting fraction if possible. The simplified fraction for our example is:

   \[ \frac{\sqrt{a}}{a} \]

Examples

• Simplify the fraction \(\frac{3}{\sqrt{5}}\):

  Multiply numerator and denominator by \(\sqrt{5}\):

  \[ \frac{3}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5} \]

  The simplified fraction is \(\frac{3\sqrt{5}}{5}\).

• Simplify the fraction \(\frac{4}{\sqrt{2}}\):

  Multiply numerator and denominator by \(\sqrt{2}\):

  \[ \frac{4}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{4\sqrt{2}}{2} = 2\sqrt{2} \]

  The simplified fraction is \(2\sqrt{2}\).

Special Cases

When dealing with more complex denominators, such as those containing sums or differences of square roots, the process involves multiplying by the conjugate of the denominator.

Example

Simplify the fraction \(\frac{2}{1 + \sqrt{3}}\):

1. Multiply the numerator and the denominator by the conjugate of the denominator. The conjugate of \(1 + \sqrt{3}\) is \(1 - \sqrt{3}\):

   \[ \frac{2}{1 + \sqrt{3}} \cdot \frac{1 - \sqrt{3}}{1 - \sqrt{3}} \]

2. Apply the difference of squares formula to the denominator:

   \[ \frac{2(1 - \sqrt{3})}{(1 + \sqrt{3})(1 - \sqrt{3})} = \frac{2(1 - \sqrt{3})}{1 - (\sqrt{3})^2} = \frac{2(1 - \sqrt{3})}{1 - 3} = \frac{2(1 - \sqrt{3})}{-2} \]

3. Simplify the fraction:

   \[ \frac{2(1 - \sqrt{3})}{-2} = -(1 - \sqrt{3}) = \sqrt{3} - 1 \]

The simplified fraction is \(\sqrt{3} - 1\).

Simplifying fractions that have square roots in the denominator is an essential skill in algebra. This process, known as rationalizing the denominator, involves transforming the fraction so that the denominator becomes a rational number. Here, we'll explore the step-by-step methods to achieve this, ensuring your fractions are in their simplest form.

Rationalizing the denominator not only simplifies the expression but also makes further calculations easier. There are two primary techniques: multiplying by the conjugate and multiplying by the square root itself. Both methods are crucial for handling different types of denominators effectively.

Let's dive into the details and examples to illustrate these techniques:

• Understanding Rationalizing the Denominator
• Basic Method: Multiplying by the Square Root
• Advanced Method: Using the Conjugate
• Step-by-Step Examples

Understanding Rationalizing the Denominator

Rationalizing the denominator involves eliminating any irrational numbers (like square roots) from the denominator of a fraction. This process makes the fraction easier to understand and work with in further mathematical operations.

Basic Method: Multiplying by the Square Root

This method is used when the denominator is a single square root. Here’s how it works:

1. Identify the square root in the denominator.
2. Multiply both the numerator and the denominator by this square root.
3. Simplify the resulting fraction.

For example:

\(\frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3}\)

Advanced Method: Using the Conjugate

When the denominator is a binomial involving a square root, multiply both the numerator and the denominator by the conjugate of the denominator. The conjugate is formed by changing the sign between the two terms.

For example, to rationalize \(\frac{2}{3+\sqrt{3}}\):

\(\frac{2}{3+\sqrt{3}} \times \frac{3-\sqrt{3}}{3-\sqrt{3}} = \frac{2(3-\sqrt{3})}{(3+\sqrt{3})(3-\sqrt{3})} = \frac{6-2\sqrt{3}}{9-3} = \frac{6-2\sqrt{3}}{6} = 1 - \frac{\sqrt{3}}{3}\)

Step-by-Step Examples

Let’s look at some detailed examples to clarify these methods:

1. Simplify \(\frac{\sqrt{18}}{3}\):
   • Step 1: Simplify the square root: \(\sqrt{18} = 3\sqrt{2}\)
   • Step 2: Simplify the fraction: \(\frac{3\sqrt{2}}{3} = \sqrt{2}\)
2. Simplify \(\frac{2}{\sqrt{12}}\):
   • Step 1: Simplify the square root: \(\sqrt{12} = 2\sqrt{3}\)
   • Step 2: Rationalize the denominator: \(\frac{2}{\sqrt{12}} \times \frac{\sqrt{12}}{\sqrt{12}} = \frac{2\sqrt{12}}{12} = \frac{2 \cdot 2\sqrt{3}}{12} = \frac{4\sqrt{3}}{12} = \frac{\sqrt{3}}{3}\)
3. Simplify \(\frac{\sqrt{6}}{\sqrt{2}}\):
   • Step 1: Simplify the fraction: \(\frac{\sqrt{6}}{\sqrt{2}} = \frac{\sqrt{6}}{\sqrt{2}} = \sqrt{\frac{6}{2}} = \sqrt{3}\)

Through practice and application of these methods, simplifying fractions with square roots in the denominator becomes intuitive and straightforward.

Square roots are fundamental in algebra and mathematics. The square root of a number \( x \) is a value that, when multiplied by itself, gives the original number \( x \). It is denoted as \( \sqrt{x} \).

• The square root of a perfect square is always an integer. For example, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
• The square root of a non-perfect square is an irrational number, which cannot be expressed as a simple fraction. For instance, \( \sqrt{2} \approx 1.414 \).

Square roots are commonly used in various mathematical operations, including solving quadratic equations and simplifying algebraic expressions. Understanding how to manipulate and simplify expressions involving square roots is crucial for progressing in math.

When simplifying fractions with square roots in the denominator, the process often involves rationalizing the denominator to eliminate the radical. This is achieved by multiplying the numerator and the denominator by a suitable value that makes the denominator a rational number.

Basic Properties of Square Roots

• Product Property: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \)
• Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)

Rationalizing the Denominator

To rationalize a denominator containing a square root, follow these steps:

1. Identify the radical in the denominator.
2. Multiply the numerator and the denominator by a value that will eliminate the radical in the denominator.
3. Simplify the resulting expression.

For example, to simplify \( \frac{1}{\sqrt{2}} \), multiply both the numerator and the denominator by \( \sqrt{2} \):

In cases where the denominator is a binomial involving square roots, use the conjugate to rationalize it. For instance, to simplify \( \frac{1}{1+\sqrt{3}} \), multiply by the conjugate \( 1-\sqrt{3} \):

When simplifying fractions with square roots in the denominator, the goal is to eliminate the square root from the denominator. This process is called rationalizing the denominator. Follow these detailed steps to simplify such fractions:

1. Simplify the Square Root: Simplify any square roots in the numerator and denominator. For example, \( \sqrt{50} \) can be simplified to \( \sqrt{25 \times 2} = 5\sqrt{2} \).

2. Rationalize the Denominator: Multiply the numerator and the denominator by the square root in the denominator. This step removes the square root from the denominator. For example, to simplify \( \frac{3}{\sqrt{2}} \), multiply both the numerator and denominator by \( \sqrt{2} \) to get:

   \[ \frac{3}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{3\sqrt{2}}{2} \]

3. Simplify the Fraction: After rationalizing the denominator, simplify the fraction if possible. For instance, if the fraction is \( \frac{6\sqrt{5}}{15} \), divide both the numerator and the denominator by their greatest common divisor:

   \[ \frac{6\sqrt{5}}{15} = \frac{2\sqrt{5}}{5} \]

Following these steps will help you simplify fractions with square roots in the denominator effectively.

Rationalizing the denominator is a process used to eliminate square roots or other irrational numbers from the denominator of a fraction. This is achieved by multiplying both the numerator and the denominator by an appropriate value that will make the denominator a rational number.

Steps to Rationalize the Denominator

1. Identify the irrational denominator: If the denominator contains a square root or another irrational number, it needs to be rationalized.

   Example: \(\frac{1}{\sqrt{2}}\)

2. Multiply by the conjugate: If the denominator is a binomial (e.g., \(a + b\sqrt{c}\)), multiply both the numerator and the denominator by the conjugate of the denominator. The conjugate is the same binomial with the opposite sign between the terms.

   Example: For \(\frac{1}{3 + \sqrt{2}}\), the conjugate is \(3 - \sqrt{2}\). Multiply both parts of the fraction by the conjugate:

   \(\frac{1}{3 + \sqrt{2}} \times \frac{3 - \sqrt{2}}{3 - \sqrt{2}} = \frac{3 - \sqrt{2}}{(3 + \sqrt{2})(3 - \sqrt{2})}\)

3. Simplify the expression: Use the difference of squares formula to simplify the denominator. The difference of squares formula states \((a + b)(a - b) = a^2 - b^2\).

   Example: \((3 + \sqrt{2})(3 - \sqrt{2}) = 3^2 - (\sqrt{2})^2 = 9 - 2 = 7\)

   So, \(\frac{3 - \sqrt{2}}{7}\)

4. Finalize the simplified form: Ensure that both the numerator and the denominator are in their simplest forms.

   Example: The final rationalized form of \(\frac{1}{3 + \sqrt{2}}\) is \(\frac{3 - \sqrt{2}}{7}\).

Examples

• Rationalize \(\frac{5}{\sqrt{3}}\):

  Multiply the numerator and denominator by \(\sqrt{3}\):

  \(\frac{5 \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \frac{5\sqrt{3}}{3}\)

• Rationalize \(\frac{4}{1 - \sqrt{5}}\):

  Multiply the numerator and denominator by the conjugate \(1 + \sqrt{5}\):

  \(\frac{4 \cdot (1 + \sqrt{5})}{(1 - \sqrt{5})(1 + \sqrt{5})} = \frac{4 + 4\sqrt{5}}{1 - 5} = \frac{4 + 4\sqrt{5}}{-4} = -1 - \sqrt{5}\)

By following these steps, you can successfully rationalize the denominator of any fraction that contains an irrational number.

Here are several examples of how to simplify fractions with square roots in the denominator:

Example 1: Simple Square Root

Simplify the fraction \(\frac{3}{\sqrt{5}}\).

1. Multiply the numerator and denominator by \(\sqrt{5}\) to rationalize the denominator: \[ \frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5} \]

Example 2: Square Roots in Both Numerator and Denominator

Simplify the fraction \(\frac{\sqrt{3}}{\sqrt{7}}\).

1. Multiply the numerator and denominator by \(\sqrt{7}\) to rationalize the denominator: \[ \frac{\sqrt{3}}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}} = \frac{\sqrt{21}}{7} \]

Example 3: Binomial Denominator

Simplify the fraction \(\frac{2}{3 + \sqrt{3}}\).

1. Multiply the numerator and denominator by the conjugate of the denominator, \(3 - \sqrt{3}\): \[ \frac{2}{3 + \sqrt{3}} \times \frac{3 - \sqrt{3}}{3 - \sqrt{3}} = \frac{2(3 - \sqrt{3})}{(3 + \sqrt{3})(3 - \sqrt{3})} \]
2. Distribute and simplify: \[ \frac{2(3 - \sqrt{3})}{3^2 - (\sqrt{3})^2} = \frac{6 - 2\sqrt{3}}{9 - 3} = \frac{6 - 2\sqrt{3}}{6} = 1 - \frac{\sqrt{3}}{3} \]

Example 4: Higher Power Roots

Simplify the fraction \(\frac{3\sqrt[4]{11}}{\sqrt[4]{2}}\).

1. Multiply the numerator and denominator by \(\sqrt[4]{8}\) to make the denominator a perfect fourth power: \[ \frac{3\sqrt[4]{11}}{\sqrt[4]{2}} \times \frac{\sqrt[4]{8}}{\sqrt[4]{8}} = \frac{3\sqrt[4]{88}}{\sqrt[4]{16}} = \frac{3\sqrt[4]{88}}{2} \]

Example 5: Combination of Square Roots and Integers

Simplify the fraction \(\frac{3 - \sqrt{5}}{2 - \sqrt{3}}\).

1. Multiply the numerator and denominator by the conjugate of the denominator, \(2 + \sqrt{3}\): \[ \frac{3 - \sqrt{5}}{2 - \sqrt{3}} \times \frac{2 + \sqrt{3}}{2 + \sqrt{3}} = \frac{(3 - \sqrt{5})(2 + \sqrt{3})}{(2 - \sqrt{3})(2 + \sqrt{3})} \]
2. Distribute and simplify: \[ \frac{6 + 3\sqrt{3} - 2\sqrt{5} - \sqrt{15}}{4 - 3} = \frac{6 + 3\sqrt{3} - 2\sqrt{5} - \sqrt{15}}{1} = 6 + 3\sqrt{3} - 2\sqrt{5} - \sqrt{15} \]

When dealing with fractions containing square roots in the denominator, special attention is required for cases involving binomials, which are expressions containing two terms. These scenarios often necessitate a slightly different approach compared to fractions with single square roots.

Here’s a structured approach to handle special cases involving binomials:

1. Difference of Squares: If the denominator is a difference of squares like \( a^2 - b^2 \), use the formula \( a^2 - b^2 = (a - b)(a + b) \) to simplify the fraction.
2. Conjugate Method: For denominators that are sums or differences involving square roots, multiply both the numerator and the denominator by the conjugate of the denominator. This process eliminates the square root from the denominator.
3. Binomial Factorization: If the binomial in the denominator can be factored into linear terms, factor it and simplify accordingly.

These methods leverage algebraic identities and properties to transform the fraction into a simpler form, ensuring ease of computation and clarity in the final result.

Practice problems are essential for mastering the art of simplifying fractions with square roots in the denominator. Here are some curated problems along with their solutions:

1. Simplify the fraction \( \frac{3}{\sqrt{5}} \).

   Solution:

   To simplify \( \frac{3}{\sqrt{5}} \), multiply both numerator and denominator by \( \sqrt{5} \) to rationalize the denominator:

   \[
   \frac{3}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5}
   \]

   Therefore, \( \frac{3}{\sqrt{5}} \) simplifies to \( \frac{3\sqrt{5}}{5} \).

2. Simplify the expression \( \frac{2}{\sqrt{3} + 1} \).

   Solution:

   To simplify \( \frac{2}{\sqrt{3} + 1} \), multiply both the numerator and the denominator by the conjugate of the denominator, \( \sqrt{3} - 1 \):

   \[
   \frac{2}{\sqrt{3} + 1} \cdot \frac{\sqrt{3} - 1}{\sqrt{3} - 1} = \frac{2(\sqrt{3} - 1)}{(\sqrt{3})^2 - 1^2}
   \]

   \[
   = \frac{2(\sqrt{3} - 1)}{3 - 1} = \frac{2(\sqrt{3} - 1)}{2} = \sqrt{3} - 1
   \]

   Thus, \( \frac{2}{\sqrt{3} + 1} \) simplifies to \( \sqrt{3} - 1 \).

3. Simplify the fraction \( \frac{4}{\sqrt{2} + \sqrt{3}} \).

   Solution:

   To simplify \( \frac{4}{\sqrt{2} + \sqrt{3}} \), multiply both numerator and denominator by \( \sqrt{2} - \sqrt{3} \) to rationalize the denominator:

   \[
   \frac{4}{\sqrt{2} + \sqrt{3}} \cdot \frac{\sqrt{2} - \sqrt{3}}{\sqrt{2} - \sqrt{3}} = \frac{4(\sqrt{2} - \sqrt{3})}{(\sqrt{2})^2 - (\sqrt{3})^2}
   \]

   \[
   = \frac{4(\sqrt{2} - \sqrt{3})}{2 - 3} = \frac{4(\sqrt{2} - \sqrt{3})}{-1} = -4(\sqrt{3} - \sqrt{2})
   \]

   Hence, \( \frac{4}{\sqrt{2} + \sqrt{3}} \) simplifies to \( -4(\sqrt{3} - \sqrt{2}) \).

When simplifying fractions with square roots in the denominator, avoid these common mistakes and follow these helpful tips for smoother calculations:

1. Forgetting to Rationalize the Denominator: Always remember to rationalize the denominator by multiplying both numerator and denominator by the conjugate of the denominator to eliminate the square root.
2. Misapplying Rules: Understand the specific rules for simplifying fractions with different types of square roots (single term, binomials) to avoid incorrect simplifications.
3. Skipping Steps: Take each step carefully and don’t skip rationalization or other necessary steps in the simplification process.
4. Ignoring Common Factors: Look for common factors that can be simplified before applying more complex methods.
5. Not Verifying Solutions: Always verify your final solution by re-checking calculations to ensure accuracy.

By being aware of these mistakes and following these tips, you can effectively simplify fractions with square roots in the denominator with confidence and accuracy.

In conclusion, mastering the art of simplifying fractions with square roots in the denominator is an essential skill in mathematics. By understanding the methods of rationalizing the denominator, applying algebraic identities, and practicing with various examples, you can confidently simplify even the most complex fractions.

Further resources and practice materials can greatly aid in reinforcing your understanding:

• Online tutorials and videos provide step-by-step guidance on different techniques.
• Mathematics textbooks often have sections dedicated to fraction simplification and algebraic manipulations.
• Practice problems and worksheets offer hands-on experience to sharpen your skills.
• Engaging with peers and educators through forums and study groups can provide additional insights and support.

Continued practice and exploration of these resources will solidify your proficiency in simplifying fractions with square roots in the denominator, making mathematics both manageable and rewarding.