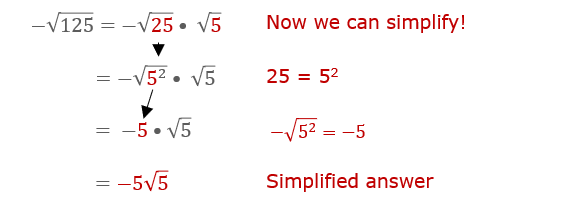Topic how to simplify square roots with variables and exponents: Learn how to simplify square roots that contain variables and exponents with our comprehensive guide. This article will help you master the techniques and rules needed to tackle these complex expressions, making your algebra skills stronger and more efficient.
Table of Content
- How to Simplify Square Roots with Variables and Exponents
- Introduction
- Understanding Square Roots
- Basic Rules of Exponents
- Factoring Under the Square Root
- Using the Product Property of Square Roots
- Simplifying Square Roots of Perfect Squares
- Combining Simplified Terms
- Examples and Step-by-Step Solutions
- Special Cases and Tips
- Common Mistakes to Avoid
- Practice Problems
- Conclusion
- YOUTUBE:
How to Simplify Square Roots with Variables and Exponents
Simplifying square roots that contain variables and exponents can seem complex at first, but by following a few simple steps, you can make the process straightforward. The goal is to express the square root in its simplest form.
Steps to Simplify Square Roots with Variables and Exponents
-
Factor the expression under the square root: Break down the expression into its prime factors. This includes both the numerical part and the variables with exponents.
Example: \( \sqrt{50x^4} \) can be factored as \( \sqrt{2 \cdot 5^2 \cdot x^4} \).
-
Apply the product property of square roots: The square root of a product is equal to the product of the square roots of each factor.
Example: \( \sqrt{2 \cdot 5^2 \cdot x^4} = \sqrt{2} \cdot \sqrt{5^2} \cdot \sqrt{x^4} \).
-
Simplify the square roots of perfect squares: Any factor that is a perfect square can be simplified by taking its square root.
Example: \( \sqrt{5^2} = 5 \) and \( \sqrt{x^4} = x^2 \).
-
Combine the simplified terms: Multiply the simplified factors together to get the simplified form of the original square root.
Example: \( 5x^2 \sqrt{2} \).
Example Problems
Let's look at some example problems to better understand the process:
-
Example 1: Simplify \( \sqrt{72x^6} \).
- Factor: \( \sqrt{72x^6} = \sqrt{2^3 \cdot 3^2 \cdot x^6} \).
- Product Property: \( \sqrt{2^3 \cdot 3^2 \cdot x^6} = \sqrt{2^3} \cdot \sqrt{3^2} \cdot \sqrt{x^6} \).
- Simplify: \( \sqrt{2^3} = 2 \sqrt{2} \), \( \sqrt{3^2} = 3 \), \( \sqrt{x^6} = x^3 \).
- Combine: \( 2 \cdot 3 \cdot x^3 \cdot \sqrt{2} = 6x^3 \sqrt{2} \).
-
Example 2: Simplify \( \sqrt{98y^8} \).
- Factor: \( \sqrt{98y^8} = \sqrt{2 \cdot 7^2 \cdot y^8} \).
- Product Property: \( \sqrt{2 \cdot 7^2 \cdot y^8} = \sqrt{2} \cdot \sqrt{7^2} \cdot \sqrt{y^8} \).
- Simplify: \( \sqrt{7^2} = 7 \) and \( \sqrt{y^8} = y^4 \).
- Combine: \( 7y^4 \sqrt{2} \).
By following these steps, you can simplify square roots that contain variables and exponents, making the expressions easier to work with and understand.

READ MORE:
Introduction
Simplifying square roots that include variables and exponents is a fundamental skill in algebra that can make solving equations and understanding higher-level mathematics much easier. This process involves breaking down complex square root expressions into their simplest form by using the properties of exponents and the rules of radicals.
Understanding how to simplify square roots is crucial because it helps in various mathematical problems, including solving equations, simplifying expressions, and working with polynomial functions. In this guide, we will explore step-by-step methods to simplify square roots with variables and exponents, ensuring you have a solid grasp of these essential concepts.
Before we dive into the methods, let's review some key concepts:
- Square Roots: The square root of a number or expression is a value that, when multiplied by itself, gives the original number or expression. For example, the square root of \( x^2 \) is \( x \).
- Exponents: Exponents represent the number of times a base is multiplied by itself. For instance, \( x^3 \) means \( x \cdot x \cdot x \).
- Product Property of Square Roots: This property states that the square root of a product is equal to the product of the square roots of each factor: \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Power Rule for Exponents: This rule is used to simplify expressions involving powers: \( (x^a)^b = x^{a \cdot b} \).
In the following sections, we will break down the process of simplifying square roots that contain variables and exponents into manageable steps. By understanding these steps, you will be able to tackle even the most complex expressions with confidence.
Understanding Square Roots
Square roots are fundamental concepts in algebra that allow us to determine a number which, when multiplied by itself, yields the original number. The symbol for the square root is √, and the number inside this symbol is called the radicand.
When dealing with square roots, it's important to understand the following key points:
- Perfect Squares: These are numbers like 1, 4, 9, 16, 25, etc., which are the squares of whole numbers. For example, √25 = 5 because 52 = 25.
- Non-Perfect Squares: These are numbers that do not yield an integer when taking their square root. For example, √20 is not an integer.
- Variables and Exponents: When variables are included under the square root, such as √(x2), the simplification involves understanding the exponent rules.
Simplifying Square Roots
To simplify square roots, especially when they include variables, follow these steps:
- Factor the Radicand: Break down the number or expression inside the square root into its prime factors or simplest form.
- For example, √72 can be factored into √(36 × 2).
- Similarly, for variables, √(x4y2) can be factored into √((x2)2y2).
- Separate the Factors: Use the property √(a × b) = √a × √b to separate the factors under the square root.
- For √72, this becomes √36 × √2 = 6√2.
- For √(x4y2), this becomes √(x2)2 × √y2 = x2y.
- Simplify the Factors: Take the square root of the perfect squares and simplify the expression.
- In our example, √72 simplifies to 6√2.
- √(x4y2) simplifies to x2y.
Examples
Let's look at a few examples to illustrate these steps:
- Simplify √(50x2):
- Factor the radicand: √(25 × 2 × x2).
- Separate the factors: √25 × √2 × √(x2).
- Simplify: 5√2 × x = 5x√2.
- Simplify √(18y3):
- Factor the radicand: √(9 × 2 × y2 × y).
- Separate the factors: √9 × √2 × √(y2) × √y.
- Simplify: 3√2 × y × √y = 3y√(2y).
Understanding these steps will help you simplify any square root, including those involving variables and exponents.
Basic Rules of Exponents
Understanding the basic rules of exponents is crucial for simplifying square roots involving variables and exponents. Here are the key rules:
-
Product of Powers:
When multiplying two exponents with the same base, you add the exponents. For example:
\(a^m \cdot a^n = a^{m+n}\)
Example: \((x^3) \cdot (x^4) = x^{3+4} = x^7\)
-
Quotient of Powers:
When dividing two exponents with the same base, you subtract the exponent of the denominator from the exponent of the numerator. For example:
\(\frac{a^m}{a^n} = a^{m-n}\)
Example: \(\frac{x^5}{x^2} = x^{5-2} = x^3\)
-
Power of a Power:
When raising an exponent to another exponent, you multiply the exponents. For example:
\((a^m)^n = a^{mn}\)
Example: \((x^2)^3 = x^{2 \cdot 3} = x^6\)
-
Power of a Product:
When raising a product to an exponent, you raise each factor to the exponent. For example:
\((ab)^m = a^m \cdot b^m\)
Example: \((2x^3y^2)^2 = 2^2 \cdot (x^3)^2 \cdot (y^2)^2 = 4x^6y^4\)
-
Power of a Quotient:
When raising a quotient to an exponent, you raise both the numerator and the denominator to the exponent. For example:
\(\left(\frac{a}{b}\right)^m = \frac{a^m}{b^m}\)
Example: \(\left(\frac{x^2}{y^3}\right)^2 = \frac{(x^2)^2}{(y^3)^2} = \frac{x^4}{y^6}\)
-
Negative Exponent:
A negative exponent represents the reciprocal of the base raised to the opposite positive exponent. For example:
\(a^{-m} = \frac{1}{a^m}\)
Example: \(x^{-3} = \frac{1}{x^3}\)
-
Zero Exponent:
Any base raised to the zero power is equal to one. For example:
\(a^0 = 1\) (assuming \(a \neq 0\))
Example: \(5^0 = 1\)
-
Fractional Exponent:
A fractional exponent represents a root of the base. For example:
\(a^{m/n} = \sqrt[n]{a^m} = \left(\sqrt[n]{a}\right)^m\)
Example: \(x^{1/2} = \sqrt{x}\)
Factoring Under the Square Root
Simplifying square roots often involves factoring the number or expression under the square root (the radicand) into its prime factors or perfect squares. This process makes it easier to identify and extract the square roots of these factors. Here’s a step-by-step guide on how to factor under the square root:
- Identify Perfect Squares:
Look for perfect square factors within the radicand. A perfect square is a number that can be expressed as the square of an integer. For example, 4, 9, 16, 25, and so on are perfect squares because they can be written as 22, 32, 42, 52, etc.
- Factor the Radicand:
Break down the radicand into its prime factors or perfect squares. For instance, if the radicand is 72, you can factor it into 36 and 2, where 36 is a perfect square.
\[\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2}\]
- Extract the Square Root of Perfect Squares:
Take the square root of the perfect square factors. Continuing with the example above:
\[\sqrt{36} = 6 \Rightarrow \sqrt{72} = 6\sqrt{2}\]
- Simplify Expressions with Variables:
When dealing with variables, factor them similarly. For example, for \(\sqrt{x^6}\):
\[\sqrt{x^6} = \sqrt{(x^3)^2} = x^3\]
For mixed expressions like \(\sqrt{9x^6}\):
\[\sqrt{9x^6} = \sqrt{9} \cdot \sqrt{x^6} = 3 \cdot x^3 = 3x^3\]
- Combining Terms:
Combine the simplified terms to get the final result. For example:
\[\sqrt{50x^4y^2} = \sqrt{25 \cdot 2 \cdot x^4 \cdot y^2} = \sqrt{25} \cdot \sqrt{2} \cdot \sqrt{x^4} \cdot \sqrt{y^2} = 5 \cdot \sqrt{2} \cdot x^2 \cdot y = 5x^2y\sqrt{2}\]
By systematically breaking down the radicand into its factors and extracting the square roots of perfect squares, you can simplify square root expressions efficiently.

Using the Product Property of Square Roots
The product property of square roots is a valuable tool when simplifying radical expressions. This property allows you to take the square root of a product of numbers and split it into the product of separate square roots. This can make complex calculations much simpler.
Here's how the product property of square roots works:
- Identify the product inside the square root. For example, consider the expression \( \sqrt{a \cdot b} \).
- Apply the product property: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \).
- Simplify each square root separately, if possible.
Let's look at an example:
Example: Simplify \( \sqrt{50} \)
- Factor 50 into its prime factors: \( 50 = 2 \cdot 5^2 \).
- Apply the product property: \( \sqrt{50} = \sqrt{2 \cdot 5^2} = \sqrt{2} \cdot \sqrt{5^2} \).
- Simplify the square root of the perfect square: \( \sqrt{5^2} = 5 \).
- Combine the results: \( \sqrt{50} = \sqrt{2} \cdot 5 \), or \( 5\sqrt{2} \).
Here's another example involving variables:
Example: Simplify \( \sqrt{18x^2} \)
- Factor 18 and the variable: \( 18x^2 = 2 \cdot 3^2 \cdot x^2 \).
- Apply the product property: \( \sqrt{18x^2} = \sqrt{2 \cdot 3^2 \cdot x^2} = \sqrt{2} \cdot \sqrt{3^2} \cdot \sqrt{x^2} \).
- Simplify the square roots: \( \sqrt{3^2} = 3 \) and \( \sqrt{x^2} = x \).
- Combine the results: \( \sqrt{18x^2} = \sqrt{2} \cdot 3 \cdot x \), or \( 3x\sqrt{2} \).
By using the product property, you can simplify square roots effectively and make calculations more manageable. Practice this method with different numbers and variables to become more comfortable with the process.
Simplifying Square Roots of Perfect Squares
Simplifying square roots of perfect squares involves identifying and factoring out perfect square factors from the radicand. Here's a step-by-step guide to help you understand the process:
- Identify the perfect square factors within the radicand.
- Rewrite the radicand as a product of perfect squares and any remaining factors.
- Apply the square root to the perfect square factors.
- Multiply the results to obtain the simplified form.
Let's look at some examples to illustrate these steps:
Example 1: Simplifying √36
- Identify the perfect square: 36 is a perfect square since
6 * 6 = 36. - Apply the square root:
√36 = 6.
√36 = 6Example 2: Simplifying √72
- Identify the perfect square factors: 72 can be factored as
36 * 2, where 36 is a perfect square. - Rewrite the expression:
√72 = √(36 * 2). - Apply the square root to the perfect square:
√(36 * 2) = √36 * √2 = 6√2.
√72 = 6√2Example 3: Simplifying √x6
- Rewrite the exponent as a power of 2:
x6 = (x3)2. - Apply the square root:
√(x3)2 = x3.
√x6 = x3Example 4: Simplifying √(49x10y8)
- Identify the perfect square factors:
49,x10, andy8are all perfect squares. - Rewrite the expression:
√(49x10y8) = √49 * √(x10) * √(y8). - Apply the square root to each factor:
√49 = 7,√(x10) = x5, and√(y8) = y4. - Combine the results:
7x5y4.
√(49x10y8) = 7x5y4By following these steps, you can simplify any square root of a perfect square efficiently. Remember to always look for perfect square factors to make the simplification process easier.
Combining Simplified Terms
Once you've simplified individual square root terms, the next step is to combine them when possible. This involves adding or subtracting like terms under the radical.
Here’s a step-by-step guide:
- Simplify each square root term individually.
- Identify like terms. Like terms under a square root must have the same radicand (the number or expression inside the square root).
- Add or subtract the coefficients of the like terms.
Let's look at an example:
Example 1:
Simplify .
Step 1: Simplify each square root term:
Step 2: Combine like terms:
Therefore, simplifies to .
By following these steps, you can simplify and combine square root terms efficiently. Remember that the key is to look for like terms and simplify each part separately before combining them.
Examples and Step-by-Step Solutions
Simplifying square roots with variables and exponents can seem challenging at first, but by following a step-by-step approach, it becomes manageable. Let's look at some examples:
Example 1
Simplify \( \sqrt{9x^6} \)
- Factor the expression under the square root to find pairs:
- Rewrite the pairs as squares:
- Separate the pairs into individual square roots:
- Simplify each square root:
- Combine the simplified terms:
\( \sqrt{3 \cdot 3 \cdot x^3 \cdot x^3} \)
\( \sqrt{3^2 \cdot (x^3)^2} \)
\( \sqrt{3^2} \cdot \sqrt{(x^3)^2} \)
\( 3 \cdot |x^3| \)
\( \sqrt{9x^6} = 3|x^3| \)
Example 2
Simplify \( \sqrt{100x^2y^4} \)
- Factor the expression under the square root to identify squared numbers and variables:
- Separate the factors into individual square roots:
- Simplify each square root:
- Combine the simplified terms:
\( \sqrt{10 \cdot 10 \cdot x^2 \cdot (y^2)^2} \)
\( \sqrt{10^2} \cdot \sqrt{x^2} \cdot \sqrt{(y^2)^2} \)
\( 10 \cdot |x| \cdot y^2 \)
\( \sqrt{100x^2y^4} = 10|x|y^2 \)
Example 3
Simplify \( \sqrt{49x^{10}y^8} \)
- Factor the expression under the square root to find pairs:
- Rewrite the pairs as squares:
- Separate the factors into individual square roots:
- Simplify each square root:
- Combine the simplified terms:
\( \sqrt{7 \cdot 7 \cdot x^5 \cdot x^5 \cdot y^4 \cdot y^4} \)
\( \sqrt{7^2 \cdot (x^5)^2 \cdot (y^4)^2} \)
\( \sqrt{7^2} \cdot \sqrt{(x^5)^2} \cdot \sqrt{(y^4)^2} \)
\( 7 \cdot |x^5| \cdot y^4 \)
\( \sqrt{49x^{10}y^8} = 7|x^5|y^4 \)
These examples illustrate the process of simplifying square roots involving variables and exponents. By factoring the expression, identifying pairs, and applying square root properties, you can simplify complex expressions step-by-step.

Special Cases and Tips
When simplifying square roots that contain variables and exponents, there are some special cases and useful tips to consider for more efficient problem-solving.
Special Cases
- Even Exponents: When a variable under the square root has an even exponent, simplify it by halving the exponent. For example, \( \sqrt{x^6} = x^3 \).
- Odd Exponents: For variables with odd exponents, split the exponent into the sum of the largest even number and one. For example, \( \sqrt{x^7} \) can be rewritten as \( \sqrt{x^6 \cdot x} = x^3 \sqrt{x} \).
- Multiple Variables: Apply the same rules to each variable separately. For instance, \( \sqrt{x^4 y^9} = x^2 y^4 \sqrt{y} \).
Tips
- Prime Factorization: Break down the number and variable parts of the radicand into their prime factors. This helps identify perfect squares more easily.
- Group Factors: Pair identical factors under the square root to simplify. For example, \( \sqrt{50x^8} = \sqrt{25 \cdot 2 \cdot x^8} = 5x^4 \sqrt{2} \).
- Check for Common Factors: Before simplifying, see if you can factor out a common factor from all terms under the square root. For example, \( \sqrt{18x^2 + 8x} = \sqrt{2x(9x + 4)} \).
By using these special cases and tips, you can simplify complex square roots involving variables and exponents more efficiently, making the process quicker and reducing the potential for errors.
Common Mistakes to Avoid
When simplifying square roots with variables and exponents, it's important to be aware of common mistakes that can lead to incorrect results. Here are some key errors to watch out for and tips on how to avoid them:
- Ignoring the Principal Square Root: Always remember that the square root symbol (√) denotes the principal (non-negative) square root. For example, √(x²) = |x|, not x, because x could be negative.
- Forgetting to Simplify Completely: Ensure that you factor out and simplify all possible perfect squares from under the square root. For example, √(72) should be simplified to 6√(2), not left as is.
- Incorrectly Simplifying Variables: When dealing with variables under the square root, remember that √(x⁴) = x², because x⁴ is a perfect square. Make sure to halve the exponents correctly when simplifying.
- Combining Terms Incorrectly: Do not combine terms under the square root unless they are like terms. For example, √(x² + y²) ≠ x + y. The square root of a sum is not the sum of the square roots.
- Mishandling Negative Radicands: The square root of a negative number involves imaginary numbers (i). For example, √(-9) = 3i, not 3. Always be aware of the context in which you are working, especially in real number solutions.
- Applying Properties Incorrectly: Ensure proper use of properties like the product and quotient properties. For instance, √(ab) = √(a) * √(b) and √(a/b) = √(a) / √(b), where both a and b are non-negative.
By keeping these common mistakes in mind and practicing careful simplification, you can avoid errors and simplify square roots with variables and exponents more effectively.
Practice Problems
Practice simplifying the following square roots involving variables and exponents. Use the steps outlined in the previous sections to break down each expression and simplify it completely.
-
Simplify the square root of \( 50x^4y^2 \):
\[
\sqrt{50x^4y^2} = \sqrt{25 \cdot 2 \cdot x^4 \cdot y^2} = \sqrt{25} \cdot \sqrt{2} \cdot \sqrt{x^4} \cdot \sqrt{y^2}
\]
\[
= 5 \cdot \sqrt{2} \cdot x^2 \cdot y = 5x^2y\sqrt{2}
\] -
Simplify the square root of \( 18x^6y^3 \):
\[
\sqrt{18x^6y^3} = \sqrt{9 \cdot 2 \cdot x^6 \cdot y^3} = \sqrt{9} \cdot \sqrt{2} \cdot \sqrt{x^6} \cdot \sqrt{y^3}
\]
\[
= 3 \cdot \sqrt{2} \cdot x^3 \cdot y^{3/2} = 3x^3y^{3/2}\sqrt{2}
\] -
Simplify the square root of \( 72x^5y \):
\[
\sqrt{72x^5y} = \sqrt{36 \cdot 2 \cdot x^4 \cdot x \cdot y} = \sqrt{36} \cdot \sqrt{2} \cdot \sqrt{x^4} \cdot \sqrt{x} \cdot \sqrt{y}
\]
\[
= 6 \cdot \sqrt{2} \cdot x^2 \cdot \sqrt{x} \cdot \sqrt{y} = 6x^2\sqrt{2xy}
\] -
Simplify the square root of \( 98x^7y^2 \):
\[
\sqrt{98x^7y^2} = \sqrt{49 \cdot 2 \cdot x^6 \cdot x \cdot y^2} = \sqrt{49} \cdot \sqrt{2} \cdot \sqrt{x^6} \cdot \sqrt{x} \cdot \sqrt{y^2}
\]
\[
= 7 \cdot \sqrt{2} \cdot x^3 \cdot \sqrt{x} \cdot y = 7x^3y\sqrt{2x}
\] -
Simplify the square root of \( 200x^8y^6 \):
\[
\sqrt{200x^8y^6} = \sqrt{100 \cdot 2 \cdot x^8 \cdot y^6} = \sqrt{100} \cdot \sqrt{2} \cdot \sqrt{x^8} \cdot \sqrt{y^6}
\]
\[
= 10 \cdot \sqrt{2} \cdot x^4 \cdot y^3 = 10x^4y^3\sqrt{2}
\]
These practice problems should help solidify your understanding of how to simplify square roots that contain variables and exponents. Ensure to follow each step carefully and verify your answers by squaring them to check if they match the original expressions.
Conclusion
Simplifying square roots with variables and exponents can initially seem daunting, but by following systematic steps, the process becomes much more manageable. Here are the key takeaways to remember:
- Always begin by factoring the expression under the square root into prime factors or perfect squares.
- Use the property that the square root of a product is the product of the square roots:
$$\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}$$ . - When dealing with variables, break them down into their even and odd power components. For example,
$$x^6 = (x^3)^2$$ . - Separate the perfect squares and simplify each part individually. For instance,
$$\sqrt{x^6} = \sqrt{(x^3)^2} = |x^3|$$ . - Always include absolute value symbols for variables with even exponents to ensure the result is non-negative.
- Combine the simplified terms to get your final expression.
Let’s consolidate this with an example:
| Example: | Simplify |
| Step 1: | Factor inside the square root: |
| Step 2: | Rewrite the expression: |
| Step 3: | Separate into individual square roots: |
| Step 4: | Simplify each square root: |
| Final Answer: |
By understanding and applying these principles, simplifying square roots with variables and exponents becomes a straightforward process. Practice consistently with different types of expressions to build confidence and mastery over time.
Remember, the key is to break down the problem into manageable steps and apply the rules systematically. Happy simplifying!

Simplifying Radicals With Variables, Exponents, Fractions, Cube Roots - Algebra
READ MORE:
Đơn giản hóa biểu thức căn bậc với biến