Mastering the Square Root of 45 in Simplest Radical Form

Understanding how to simplify the square root of 45 involves breaking it down into its prime factors and simplifying the radical expression. Here’s a comprehensive guide to achieve that:

Prime Factorization

The first step is to express 45 as a product of its prime factors:

\[
45 = 3 \times 3 \times 5 = 3^2 \times 5
\]

Simplifying the Radical

Next, we use the property of square roots that states \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) to simplify the square root of 45:

\[
\sqrt{45} = \sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5} = 3\sqrt{5}
\]

Final Simplified Form

Therefore, the simplest radical form of the square root of 45 is:

\[
\sqrt{45} = 3\sqrt{5}
\]

Step-by-Step Simplification Process

1. Start with the number 45.
2. Find the prime factorization: \(45 = 3 \times 3 \times 5\).
3. Group the prime factors into pairs: \(45 = 3^2 \times 5\).
4. Apply the square root to each pair: \(\sqrt{45} = \sqrt{3^2 \times 5}\).
5. Simplify the square root of the pair: \(\sqrt{3^2} = 3\).
6. Multiply the simplified square root by the remaining factor: \(3\sqrt{5}\).

Verification

To verify, we can square the simplified form and check if it equals the original number:

\[
(3\sqrt{5})^2 = 3^2 \times (\sqrt{5})^2 = 9 \times 5 = 45
\]

Since the squared result is 45, the simplification is verified to be correct.

Conclusion

Simplifying the square root of 45 involves prime factorization and the application of square root properties. The simplest radical form of \(\sqrt{45}\) is \(3\sqrt{5}\), as demonstrated above.

Square roots are fundamental in mathematics, representing a value that, when multiplied by itself, gives the original number. Understanding square roots is essential for solving various mathematical problems and equations.

Key points about square roots:

• The square root of a number \( x \) is written as \( \sqrt{x} \).
• Square roots can be positive or negative since both \((\sqrt{x})^2\) and \((- \sqrt{x})^2\) equal \( x \).
• Square roots of perfect squares are integers (e.g., \( \sqrt{16} = 4 \) or \( \sqrt{25} = 5 \)).
• Non-perfect squares result in irrational numbers (e.g., \( \sqrt{2} \approx 1.414 \)).

Steps to understand square roots:

1. Identify the number for which you want to find the square root.
2. Determine if the number is a perfect square. If so, the square root will be an integer.
3. If the number is not a perfect square, estimate the square root or simplify it to its radical form.
4. Use prime factorization to simplify the square root, if necessary.

For example, to find the square root of 45, we can use the prime factorization method:

• First, express 45 as a product of its prime factors: \( 45 = 3 \times 3 \times 5 = 3^2 \times 5 \).
• Next, apply the square root to each factor: \( \sqrt{45} = \sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5} = 3\sqrt{5} \).

Thus, the square root of 45 in its simplest radical form is \( 3\sqrt{5} \). Understanding how to simplify square roots helps in various mathematical applications, making complex calculations more manageable.

The simplest radical form of a square root is achieved by expressing the number under the square root as a product of its prime factors and then simplifying. This form is beneficial for making calculations easier and for providing a clear, concise representation of the number.

Key concepts for understanding simplest radical form:

• Prime Factorization: Breaking down a number into its prime factors helps in simplifying the square root.
• Perfect Squares: Identifying perfect squares within the factorization allows for simplification.
• Properties of Square Roots: Using the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) to separate factors.

Steps to simplify a square root to its simplest radical form:

1. Find the Prime Factors: Determine the prime factors of the number. For 45, the prime factors are \( 3 \times 3 \times 5 \) or \( 3^2 \times 5 \).
2. Group the Factors: Group the prime factors into pairs of identical factors. Here, \( 3^2 \) forms a pair.
3. Apply the Square Root: Apply the square root to each group of factors:

   
   \[
   \sqrt{45} = \sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5} = 3\sqrt{5}
   \]

4. Simplify: Simplify the expression by taking the square root of the perfect squares and multiplying any remaining factors under the square root.

Therefore, the simplest radical form of \(\sqrt{45}\) is \(3\sqrt{5}\). Simplifying to this form involves identifying and extracting perfect squares from under the radical, resulting in a more streamlined and manageable expression.

The prime factorization method is a systematic approach to simplifying the square root of a number by expressing it as a product of its prime factors. This method makes it easier to identify and extract perfect squares, leading to a simplified radical form.

Steps to simplify the square root of 45 using the prime factorization method:

1. Find the Prime Factors: Determine the prime factors of 45.

   Prime factorization of 45:

   
   \[
   45 = 3 \times 3 \times 5 = 3^2 \times 5
   \]

2. Group the Factors: Group the prime factors into pairs of identical factors.

   In this case, \( 3^2 \) forms a pair, and 5 remains unpaired.

3. Apply the Square Root: Apply the square root to each group of factors.

   Using the property of square roots \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):

   
   \[
   \sqrt{45} = \sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5}
   \]

4. Simplify: Simplify the expression by taking the square root of the perfect squares and leaving any remaining factors under the square root.

   Since \(\sqrt{3^2} = 3\), we have:

   
   \[
   \sqrt{45} = 3 \times \sqrt{5} = 3\sqrt{5}
   \]

By following these steps, we find that the square root of 45 simplifies to \( 3\sqrt{5} \). This method highlights the importance of prime factorization in simplifying radicals and demonstrates how perfect squares can be extracted to achieve the simplest form.

Simplifying the square root of 45 involves breaking it down into its prime factors and then simplifying the expression step by step. Here is a detailed guide to simplify \(\sqrt{45}\) to its simplest radical form:

1. Identify the Number:

   We begin with the number 45, which we want to simplify.

2. Prime Factorization:

   Break down 45 into its prime factors:

   
   \[
   45 = 3 \times 3 \times 5 = 3^2 \times 5
   \]

3. Group the Factors:

   Group the prime factors into pairs of identical factors. In this case, we have a pair of 3s and a single 5:

   
   \[
   3^2 \times 5
   \]

4. Apply the Square Root:

   Apply the square root to each group of factors using the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):

   
   \[
   \sqrt{45} = \sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5}
   \]

5. Simplify:

   Simplify the expression by taking the square root of the perfect squares. Since \(\sqrt{3^2} = 3\), we get:

   
   \[
   \sqrt{3^2} \times \sqrt{5} = 3 \times \sqrt{5}
   \]

6. Result:

   Thus, the simplified form of \(\sqrt{45}\) is:

   
   \[
   \sqrt{45} = 3\sqrt{5}
   \]

By following these steps, we have successfully simplified the square root of 45 to its simplest radical form, \(3\sqrt{5}\). This method demonstrates the importance of prime factorization and the properties of square roots in simplifying radical expressions.

Verifying the simplified form of a square root ensures the accuracy of the simplification process. For the square root of 45, we simplified it to \(3\sqrt{5}\). To verify this, we can square the simplified form and check if it equals the original number.

Steps to verify the simplified form:

1. Start with the Simplified Form:

   The simplified form of \(\sqrt{45}\) is \(3\sqrt{5}\).

2. Square the Simplified Form:

   Square \(3\sqrt{5}\) to check if it equals 45:

   
   \[
   (3\sqrt{5})^2
   \]

3. Apply the Exponent:

   Apply the exponent to both the coefficient and the radical part:

   
   \[
   (3\sqrt{5})^2 = 3^2 \times (\sqrt{5})^2
   \]

4. Calculate the Squares:

   Calculate the square of 3 and the square of \(\sqrt{5}\):

   
   \[
   3^2 = 9 \quad \text{and} \quad (\sqrt{5})^2 = 5
   \]

5. Multiply the Results:

   Multiply the squared values together:

   
   \[
   9 \times 5 = 45
   \]

6. Conclusion:

   Since squaring \(3\sqrt{5}\) results in 45, our simplified form is verified to be correct.

This verification process confirms that the simplest radical form of \(\sqrt{45}\) is indeed \(3\sqrt{5}\). Ensuring the accuracy of our simplification helps in maintaining mathematical precision and reliability.

Besides the prime factorization method, there are alternative methods to simplify the square root of 45. These methods offer different perspectives and can be useful depending on the context.

Method 1: Estimation and Refinement

One way to simplify a square root is to use estimation and then refine the estimate to get a more accurate result.

1. Estimate the Square Root:

   Identify the two perfect squares between which 45 lies. In this case, \(36\) (which is \(6^2\)) and \(49\) (which is \(7^2\)). Thus, \(\sqrt{45}\) is between 6 and 7.

2. Refine the Estimate:

   Since 45 is closer to 49 than to 36, refine the estimate to be closer to 7. Through iterative approximation, you can get a more precise value.

Method 2: Using the Properties of Square Roots

Leverage the properties of square roots to simplify \(\sqrt{45}\).

1. Break Down the Number:

   Express 45 as a product of a perfect square and another number:

   
   \[
   45 = 9 \times 5
   \]

2. Apply the Square Root Property:

   Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):

   
   \[
   \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5}
   \]

3. Simplify the Expression:

   Simplify the square root of the perfect square:

   
   \[
   \sqrt{9} = 3
   \]

   Thus:

   
   \[
   \sqrt{45} = 3\sqrt{5}
   \]

Method 3: Visual Representation

Visual methods can also help in understanding the simplification process. Consider using geometric representations or number line diagrams to visualize the simplification of square roots.

1. Geometric Representation:

   Draw a square with an area of 45 square units and then decompose it into smaller squares to identify perfect squares within.

2. Number Line Diagram:

   Place the square root of 45 on a number line between the square roots of 36 and 49 to visually estimate and then refine its value.

These alternative methods provide additional tools to simplify the square root of 45, each with its unique advantages. Understanding and applying different approaches can enhance mathematical flexibility and problem-solving skills.

Simplifying the square root of 45 to its simplest radical form can be straightforward, but there are common mistakes students make. Here are some of those mistakes and how to avoid them:

• Incorrect Prime Factorization:

  A common mistake is not breaking down the number correctly into its prime factors. For example, the correct factorization of 45 is 3 × 3 × 5. Ensure to double-check your factorization before proceeding.

• Ignoring Perfect Squares:

  Students often miss identifying the largest perfect square factor. For 45, the largest perfect square factor is 9 (since 45 = 9 × 5). Recognize and extract these perfect squares to simplify the radical correctly.

• Forgetting to Simplify Fully:

  After breaking down the factors, students might stop too soon. For example, they may stop at √(9 × 5) but not simplify further to 3√5. Always ensure that your final expression is in its simplest form.

• Incorrect Multiplication:

  When simplifying, ensure accurate multiplication and factorization. Errors in basic arithmetic can lead to incorrect results. Verify your calculations at each step.

• Improper Handling of Variables:

  If variables are involved, make sure to handle their exponents correctly, especially when they are under a radical. Simplify the variables along with the numerical part of the radical.

Steps to Avoid These Mistakes:

1. Always start with the prime factorization of the number.
2. Identify and extract the largest perfect square factor.
3. Simplify the square root of the perfect square factor.
4. Multiply the simplified root with any remaining factors under the radical.
5. Double-check each step for arithmetic accuracy.

By following these steps and being aware of these common mistakes, you can ensure that you simplify square roots correctly every time.

Simplifying radicals, such as the square root of 45, has practical applications across various fields. Understanding these applications helps in appreciating the importance of mastering radical simplification.

Here are some common practical applications:

• Geometry:

  In geometry, simplifying radicals is essential for calculating lengths, areas, and volumes. For instance, if a square room has an area of 45 square feet, the side length can be found using the square root of 45, which simplifies to \(3\sqrt{5}\) feet.

• Engineering:

  Engineers often encounter radicals when working with physical dimensions and forces. Simplifying these radicals can make calculations more manageable and results easier to interpret.

• Physics:

  In physics, many formulas involve square roots, such as those for calculating velocities, accelerations, and other quantities. Simplifying the square roots can help in simplifying the overall equations.

• Computer Science:

  Algorithms in computer graphics and machine learning sometimes involve square roots. Simplifying these values can optimize computations and improve performance.

• Real-life Scenarios:

  In everyday life, simplified radicals can be used for practical problem-solving, such as determining the dimensions of materials needed for construction projects or understanding the scale of models.

By recognizing these practical applications, the relevance of simplifying radicals extends beyond theoretical mathematics into tangible, real-world scenarios.

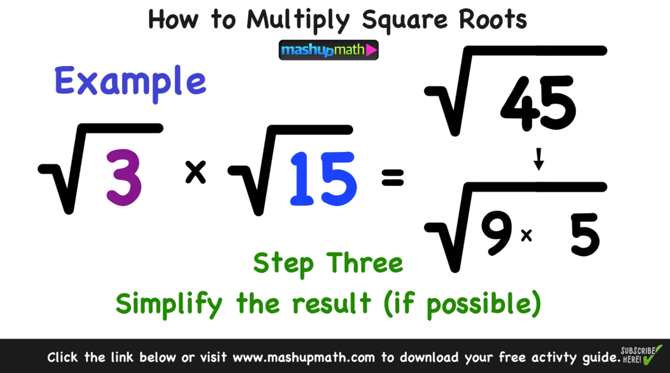
The process of simplifying the square root of 45 has highlighted several important mathematical concepts. By using prime factorization, we broke down 45 into its prime components and discovered that it can be expressed as the product of 9 and 5. This allowed us to simplify the square root of 45 into its simplest radical form: \( 3\sqrt{5} \).

Understanding that 45 is not a perfect square is crucial, as it reinforces the notion that its square root remains an irrational number. This means that \( \sqrt{45} \) cannot be expressed as a simple fraction, but rather as an infinite, non-repeating decimal, approximately equal to 6.708.

Through this exercise, we have not only learned the specific steps to simplify the square root of 45, but also gained insight into the broader applications of simplifying radicals in various mathematical contexts. This knowledge is foundational for more advanced topics in algebra and beyond.

In summary, the key takeaways are:

• The prime factorization method helps in breaking down composite numbers into their prime factors.
• Simplifying square roots involves identifying and extracting perfect squares from under the radical.
• The simplified form of \( \sqrt{45} \) is \( 3\sqrt{5} \), which is an irrational number.
• Simplifying radicals is an essential skill for solving more complex mathematical problems and for practical applications in various fields.

By mastering these concepts, one can confidently approach and solve problems involving radicals and square roots, thereby enhancing their mathematical proficiency.