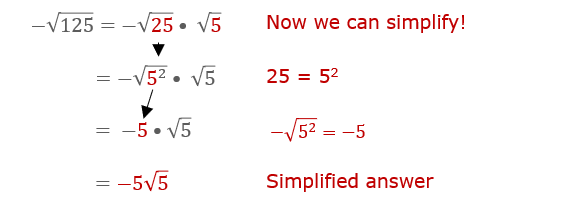Topic decimal to square root calculator: Discover the ease of converting decimals to square roots with our comprehensive guide. Learn how to use a decimal to square root calculator, understand the underlying concepts, and explore practical examples. Whether you're a student or a math enthusiast, this guide simplifies complex calculations and enhances your mathematical skills.
Table of Content
- Decimal to Square Root Calculator
- Introduction to Decimal to Square Root Calculators
- How to Use a Decimal to Square Root Calculator
- Steps to Calculate Square Roots
- Examples of Square Root Calculations
- Perfect Squares and Their Roots
- Calculating Square Roots of Non-Perfect Squares
- Square Roots of Negative Numbers
- Square Root Properties and Formulas
- Common Square Root Errors
- Advanced Square Root Calculations
- Alternative Methods to Calculate Square Roots
- Applications of Square Roots in Real Life
- Related Calculators and Tools
- FAQs About Square Root Calculators
- YOUTUBE: Tìm hiểu cách chuyển đổi số thập phân thành dạng căn bậc hai với video hướng dẫn chi tiết. Thu hút người xem bằng các bước dễ hiểu và chính xác.
Decimal to Square Root Calculator
Use the Decimal to Square Root Calculator to find the square root of any decimal number. This tool simplifies the process of determining the square root, whether the number is a perfect square or not. Below is a detailed guide on how to use the calculator and some example calculations.
Steps to Use the Calculator
- Enter the decimal number for which you want to calculate the square root.
- Click the "Calculate" button to get the result.
- The calculator will provide the square root in both exact form (if applicable) and decimal form.
Example Calculations
| Input Number | Square Root |
|---|---|
| 0.25 | \(\sqrt{0.25} = 0.5\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 10 | \(\sqrt{10} \approx 3.162\) |
Understanding Square Roots
The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). For example, the square root of 25 is 5 because \(5^2 = 25\). When dealing with non-perfect squares, the result will be an irrational number (a non-repeating, non-terminating decimal).
Simplifying Square Roots
- Identify any perfect square factors of the number.
- Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) to simplify.
- For example, \(\sqrt{27} = \sqrt{9 \times 3} = \sqrt{9} \times \sqrt{3} = 3\sqrt{3}\).
Additional Features
This calculator also provides the principal square root (positive root) and, where applicable, the negative root. For instance, the square roots of 9 are 3 and -3, as both satisfy the equation \(y^2 = 9\).
Explore more advanced calculations such as cube roots and n-th roots using similar methods.
Use the Decimal to Square Root Calculator to quickly find the square roots of decimal numbers with ease!

READ MORE:
Introduction to Decimal to Square Root Calculators
Decimal to square root calculators are essential tools for students, mathematicians, and anyone dealing with numerical computations. These calculators simplify the process of finding the square root of a given decimal number, providing quick and accurate results. Whether you are working with perfect squares or non-perfect squares, these calculators can handle various scenarios, offering both exact and approximate values. They are invaluable in educational settings, helping to demystify complex mathematical concepts and making problem-solving more efficient.
How to Use a Decimal to Square Root Calculator
A decimal to square root calculator is a handy tool for quickly finding the square root of decimal numbers. Here's a step-by-step guide on how to use such a calculator effectively:
-
Enter the Decimal Number:
Start by inputting the decimal number you wish to find the square root of. Most calculators have a dedicated input field for this purpose.
-
Select or Confirm Square Root Operation:
Ensure that the calculator is set to perform the square root operation. Some calculators might have multiple functions, so you may need to select the square root (√) option.
-
Initiate the Calculation:
Press the 'Calculate' button (often labeled with '=' or '√'). The calculator will process the input and display the square root of the decimal number.
-
View the Result:
The result will appear on the screen. For most decimal numbers, the output will be a decimal approximation. For example, the square root of 0.25 will display as 0.5.
-
Check for Additional Information:
Some calculators provide additional information, such as whether the number is a perfect square or offer detailed steps on how the calculation was performed.
-
Explore Advanced Options:
Advanced calculators may allow you to see the result in different forms, such as simplified radicals or exact values. Utilize these features if needed for your calculations.
Using a decimal to square root calculator is straightforward, but knowing these steps can help you get the most accurate and useful results.
| Step | Action | Example |
|---|---|---|
| 1 | Enter the Decimal Number | 0.64 |
| 2 | Select Square Root Operation | √ |
| 3 | Initiate Calculation | Calculate |
| 4 | View Result | 0.8 |
For practical usage, you might also want to understand how the calculator handles non-perfect squares and how it approximates the square roots of irrational numbers. This knowledge can be particularly helpful in fields that require precise calculations.
Additionally, if you're interested in manual calculations or understanding the mathematical principles behind square roots, explore the other sections of this guide.
Steps to Calculate Square Roots
Calculating the square root of a number can be done through various methods. One traditional and manual approach is the long division method. Here is a step-by-step guide to calculate square roots using this method:
-
Start with the number:
Write the number for which you want to find the square root. If it's a whole number, add decimal points and pairs of zeros if needed.
For example, to find the square root of 7921, write it as 79 21.
-
Pair the digits:
Separate the number into pairs of digits starting from the decimal point towards the left and right. If the number of digits is odd, the first digit stands alone.
For 7921, the pairs are (79) (21).
-
Find the largest integer:
Find the largest integer whose square is less than or equal to the first pair. Write this integer above the pair and its square below the pair. Subtract to find the remainder.
For the pair 79, the largest integer is 8, because \(8^2 = 64\). Subtract 64 from 79 to get 15.
-
Bring down the next pair:
Bring down the next pair of digits next to the remainder to form a new number. For example, bring down 21 to get 1521.
-
Double the current quotient:
Double the quotient obtained so far (8) to get 16. Place it as the new divisor, leaving a blank for the next digit. Find a digit to place in both the blank spots such that the product is less than or equal to the new number.
For 16_, find the largest digit x such that \(16x \times x \leq 1521\). The digit is 9, since \(169 \times 9 = 1521\).
-
Repeat the process:
Continue the process by bringing down pairs of zeros, finding new digits, and subtracting until you achieve the desired accuracy. If you are working with decimals, continue until you reach the desired number of decimal places.
In this case, the square root of 7921 is 89.
The steps above can also be used to find the square root of decimal numbers. Simply extend the number with pairs of zeros and follow the same process.
Here is a simplified example of finding the square root of a smaller number:
- Find the square root of 6.25.
- Write it as \(6.25 = 625/100\).
- Calculate the square roots of the numerator and the denominator separately: \(√625 = 25\) and \(√100 = 10\).
- Thus, \(√6.25 = 25/10 = 2.5\).
Using the long division method allows you to find square roots manually and is especially useful when a calculator is not available. It also provides a deeper understanding of the concept and process behind square roots.
Examples of Square Root Calculations
Understanding square roots is easier with practical examples. Here are detailed calculations for both perfect squares and non-perfect squares, including decimal numbers and how to handle negative numbers:
1. Perfect Squares
Perfect squares are numbers whose square roots are whole numbers. For example:
- Square Root of 36:
Since \(36 = 6 \times 6\), the square root of 36 is 6.
\( \sqrt{36} = 6 \)
- Square Root of 81:
Since \(81 = 9 \times 9\), the square root of 81 is 9.
\( \sqrt{81} = 9 \)
2. Non-Perfect Squares
For non-perfect squares, the square root is not an integer and often involves decimals or irrational numbers. For example:
- Square Root of 20:
20 is not a perfect square. Using a calculator or approximation methods, we find:
\( \sqrt{20} \approx 4.472 \)
- Square Root of 50:
50 is also not a perfect square. Using a calculator, we get:
\( \sqrt{50} \approx 7.071 \)
3. Decimal Numbers
Calculating the square root of decimal numbers follows the same principle. Here are a few examples:
- Square Root of 0.25:
Since \(0.25 = (0.5)^2\), the square root of 0.25 is 0.5.
\( \sqrt{0.25} = 0.5 \)
- Square Root of 2.25:
2.25 is not a perfect square, but its square root can be calculated as:
\( \sqrt{2.25} = 1.5 \)
4. Negative Numbers
The square root of negative numbers involves imaginary numbers since a real number squared cannot be negative. For example:
- Square Root of -9:
The square root of -9 is expressed using the imaginary unit \(i\), where \(i = \sqrt{-1}\). Therefore:
\( \sqrt{-9} = 3i \)
- Square Root of -16:
Similarly, the square root of -16 is:
\( \sqrt{-16} = 4i \)
5. Using a Decimal to Square Root Calculator
To find the square root of a decimal or any number using a calculator, follow these steps:
- Enter the decimal number into the calculator.
- Select the square root function (often represented by the √ symbol).
- Press the calculate or equals button.
- View the result, which will often be a decimal or a fraction.
Below is a table summarizing some examples:
| Number | Square Root | Type |
|---|---|---|
| 49 | 7 | Perfect Square |
| 45 | \( \approx 6.708 \) | Non-Perfect Square |
| 0.64 | 0.8 | Decimal |
| -25 | 5i | Imaginary |
These examples illustrate how to calculate square roots across different types of numbers. Practice with a variety of examples to become more familiar with the process.

Perfect Squares and Their Roots
Perfect squares are numbers that can be expressed as the product of an integer with itself. In other words, a perfect square is a number that is the square of an integer. For example, 9 is a perfect square because it can be written as \(3 \times 3\) or \(3^2\).
Here is a list of perfect squares from 1 to 100, along with their square roots:
| Number | Square Root | Square |
|---|---|---|
| 1 | \(\sqrt{1} = 1\) | 1 = \(1 \times 1\) |
| 4 | \(\sqrt{4} = 2\) | 4 = \(2 \times 2\) |
| 9 | \(\sqrt{9} = 3\) | 9 = \(3 \times 3\) |
| 16 | \(\sqrt{16} = 4\) | 16 = \(4 \times 4\) |
| 25 | \(\sqrt{25} = 5\) | 25 = \(5 \times 5\) |
| 36 | \(\sqrt{36} = 6\) | 36 = \(6 \times 6\) |
| 49 | \(\sqrt{49} = 7\) | 49 = \(7 \times 7\) |
| 64 | \(\sqrt{64} = 8\) | 64 = \(8 \times 8\) |
| 81 | \(\sqrt{81} = 9\) | 81 = \(9 \times 9\) |
| 100 | \(\sqrt{100} = 10\) | 100 = \(10 \times 10\) |
Perfect squares have interesting properties:
- The square of an even number is always even, and the square of an odd number is always odd.
- The last digit of a perfect square is predictable:
- If a number ends in 1 or 9, its square ends in 1.
- If a number ends in 4 or 6, its square ends in 6.
- If a number ends in 5, its square ends in 5.
- If a number ends in 0, its square ends in 0.
- The sum of the first \(n\) odd numbers is always a perfect square.
- The difference between the squares of two consecutive integers is always an odd number.
Perfect squares play a crucial role in algebra and number theory, helping to simplify expressions and solve equations involving quadratic forms.
Calculating Square Roots of Non-Perfect Squares
Calculating the square root of a non-perfect square involves several steps and methods. Here's a detailed guide to help you understand the process:
-
Estimation: Start by estimating the square root. This can be done by finding the closest perfect squares between which your number lies. For example, if you want to find the square root of 20, you know it lies between the square roots of 16 (4) and 25 (5).
-
Long Division Method: This method involves dividing the number into pairs of digits starting from the decimal point and applying a process similar to long division.
- Divide the number into pairs of digits from the decimal point.
- Estimate the largest integer whose square is less than or equal to the leftmost pair. Subtract its square from the leftmost pair and bring down the next pair of digits.
- Double the quotient obtained and use it as a new divisor. Find the largest digit to append to the quotient so that the new product is less than or equal to the current dividend.
- Repeat the process for the required number of decimal places.
-
Using a Calculator: Many online calculators can compute the square roots of non-perfect squares efficiently. Simply input the number and choose the "Square Root" function to get both the exact and decimal forms of the root.
For example, let's find the square root of 27:
| Step | Calculation |
| 1 | Estimate: between 5 and 6 |
| 2 | 5.2 * 5.2 = 27.04 (too high), 5.1 * 5.1 = 26.01 (too low) |
| 3 | 5.15 * 5.15 = 26.5225 (too low), 5.16 * 5.16 = 26.6256 (too low) |
| 4 | 5.17 * 5.17 = 26.729 (too low), 5.18 * 5.18 = 26.8324 (too low) |
| 5 | Continue until the desired precision is achieved. |
By refining the estimation step-by-step, you can approximate the square root of non-perfect squares to your desired precision. Alternatively, using an online square root calculator can save time and provide quick, accurate results.
Calculating square roots of non-perfect squares might seem challenging, but with practice and the right tools, it becomes much easier. Happy calculating!
Square Roots of Negative Numbers
Calculating the square root of negative numbers involves dealing with imaginary numbers. When you take the square root of a negative number, the result is not a real number but an imaginary number, represented by the symbol i, where i is defined as the square root of -1.
Here are the steps to calculate the square root of a negative number:
- Identify the negative number you want to find the square root of. For example, let's consider the number -25.
- Express the negative number in terms of i. Since i is the square root of -1, we can write -25 as 25 × (-1).
- Separate the square root operation. This gives us:
\[ \sqrt{-25} = \sqrt{25 \times (-1)} = \sqrt{25} \times \sqrt{-1} \] - Calculate the square root of the positive part of the number. In this case, \(\sqrt{25} = 5\).
- Multiply the result by i. Thus, the square root of -25 is: \[ 5i \]
Let's look at another example:
- Example: Find the square root of -81.
- Step 1: Express -81 as 81 × (-1).
- Step 2: Separate the square root operation: \[ \sqrt{-81} = \sqrt{81 \times (-1)} = \sqrt{81} \times \sqrt{-1} \]
- Step 3: Calculate the square root of 81: \[ \sqrt{81} = 9 \]
- Step 4: Multiply by i: \[ 9i \]
- Therefore, the square root of -81 is \(9i\).
For more complex numbers, the process involves additional steps, but the core concept remains the same: separating the real and imaginary parts and then combining them. This can be represented as:
\[
\sqrt{a + bi} = c + di
\]
Where \( c \) and \( d \) are calculated using specific formulas:
\[
c = \frac{1}{\sqrt{2}} \times \sqrt{\sqrt{a^2 + b^2} + a}
\]
\[
d = \frac{\text{sign}(b)}{\sqrt{2}} \times \sqrt{\sqrt{a^2 + b^2} - a}
\]
Square Root Properties and Formulas
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol (√). Here are some key properties and formulas related to square roots:
Properties of Square Roots
- Product Property: The square root of a product is equal to the product of the square roots of each factor.
\[
\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}
\] - Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator.
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\] - Square of a Square Root: The square of a square root returns the original number.
\[
(\sqrt{a})^2 = a
\] - Square Root of a Power: The square root of a number raised to a power is the same as the number raised to half the power.
\[
\sqrt{a^n} = a^{n/2}
\]
Formulas Involving Square Roots
| Formula | Description |
| \[ \sqrt{a^2} = a \] | The square root of a squared number is the absolute value of the original number. |
| \[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \] | The square root of a product is equal to the product of the square roots. |
| \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \] | The square root of a quotient is the quotient of the square roots. |
| \[ (\sqrt{a})^2 = a \] | The square of a square root returns the original number. |
Special Cases
- Square Root of Zero: The square root of zero is zero.
\[
\sqrt{0} = 0
\] - Square Root of One: The square root of one is one.
\[
\sqrt{1} = 1
\]
Understanding these properties and formulas is crucial for solving equations involving square roots and for various applications in geometry and algebra.

Common Square Root Errors
Understanding common errors in square root calculations is crucial for accuracy. Here are some frequent mistakes and how to avoid them:
- Incorrectly Adding Square Roots: It's a common misconception that √a + √b = √(a + b). In reality, the sum of square roots should be left in their simplified form, such as √2 + √3.
- Misplacing Decimal Points: When dealing with decimals, always ensure the decimal point is correctly placed. For instance, the square root of 2.56 is 1.6, not 0.16 or 16.
- Ignoring Negative Solutions: While square roots of positive numbers are straightforward, remember that square roots of negative numbers involve imaginary numbers. For example, √(-4) = 2i.
- Forgetting to Simplify: Always simplify the square roots of non-perfect squares. For example, √45 can be simplified to 3√5.
- Errors in Long Division Method: When using the long division method for square roots, mistakes often occur in the iterative steps. Ensure each step is followed meticulously.
Let's delve into an example to understand these errors better:
Example: Simplifying Square Roots
Consider the square root of 50:
- Find the factors of 50: 1, 2, 5, 10, 25, 50.
- Identify the perfect square among the factors: 25.
- Rewrite 50 as a product of its factors: 50 = 25 x 2.
- Simplify using the property √(a x b) = √a x √b: √50 = √25 x √2 = 5√2.
By avoiding these common errors and following systematic steps, the accuracy of square root calculations can be significantly improved.
Advanced Square Root Calculations
Advanced square root calculations involve a variety of techniques and principles to handle more complex scenarios. Below are detailed explanations and step-by-step instructions on these methods.
Estimating Square Roots Manually
When a precise value is not necessary, estimation can be useful. Here’s how to estimate square roots manually:
- Identify two perfect squares between which the number lies. For example, to estimate √50, note that 49 (7²) and 64 (8²) are close.
- Determine that the square root will be between 7 and 8.
- Refine your estimate by averaging 7 and 8: (7 + 8) / 2 = 7.5.
- Square 7.5 to check how close it is to 50: 7.5² = 56.25. Since 56.25 is greater than 50, try a lower value like 7.1.
- Continue this process iteratively until the estimate is sufficiently close to the actual square root.
Newton's Method for Finding Square Roots
Newton's method (also known as the Newton-Raphson method) is an efficient algorithm for finding approximations of roots. Here’s how it works:
- Start with an initial guess \( x_0 \). For example, for √50, let’s start with \( x_0 = 7 \).
- Apply the formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \) where S is the number whose square root is being calculated. So, \( x_1 = \frac{1}{2} \left( 7 + \frac{50}{7} \right) = 7.071 \).
- Repeat the process with \( x_1 \): \( x_2 = \frac{1}{2} \left( 7.071 + \frac{50}{7.071} \right) \approx 7.071 \).
- Continue iterating until \( x_{n+1} \) is close enough to \( x_n \). After several iterations, the value will converge to the square root of 50.
Using Decimal Calculators for Square Roots
When precision is crucial, using a calculator is the most reliable method. Here’s how to calculate square roots using a decimal calculator:
- Input the number (e.g., 50) into the calculator.
- Select the square root function, often labeled as \( \sqrt{} \) or with a radical symbol.
- Read the result displayed. Most scientific calculators will show several decimal places for higher accuracy.
- For very precise calculations, use calculators that support high-precision decimal operations or software designed for mathematical computations.
Special Cases: Square Roots of Negative Numbers
Square roots of negative numbers are not real numbers. Instead, they are expressed in terms of imaginary units. Here’s how to handle them:
- Understand that \( \sqrt{-1} = i \), where \( i \) is the imaginary unit.
- To find the square root of a negative number, separate the negative sign and use the imaginary unit. For example, \( \sqrt{-16} = \sqrt{16} \cdot \sqrt{-1} = 4i \).
Square Roots and Algebraic Properties
Square roots follow several important algebraic properties:
- Multiplication: \( \sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b} \)
- Division: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- Addition/Subtraction: Square roots can only be directly added or subtracted if they have the same radicand (e.g., \( \sqrt{a} + \sqrt{a} = 2\sqrt{a} \)).
- Rationalizing the Denominator: To remove a square root from the denominator, multiply the numerator and denominator by the conjugate of the denominator.
Applications of Advanced Square Root Calculations
Advanced square root calculations are used in various fields, including:
- Engineering and Physics: For solving equations involving quadratic forms and wave functions.
- Finance: For calculating compound interest and financial modeling.
- Computer Science: In algorithms for data analysis and machine learning.
Alternative Methods to Calculate Square Roots
Calculating square roots can be done using several methods beyond the basic calculator function. Here, we explore some alternative methods for finding square roots:
1. Long Division Method
The long division method is a manual technique to find square roots and is particularly useful when a calculator is not available.
- Group the digits of the number in pairs, starting from the decimal point.
- Find the largest integer whose square is less than or equal to the first pair or single digit.
- Subtract this square from the first pair and bring down the next pair of digits.
- Double the result obtained so far and use it as the new divisor.
- Repeat the process until you reach the desired precision.
2. Babylonian Method (Heron’s Method)
This iterative method uses an initial guess to approximate the square root and refines it through successive iterations.
- Start with an initial guess, \( x_0 \), for the square root of the number \( a \).
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{a}{x_n} \right) \) to find a better approximation.
- Repeat the iteration until the difference between successive approximations is within a desired tolerance.
For example, to find \( \sqrt{16} \):
- Initial guess, \( x_0 = 4 \)
- First iteration, \( x_1 = \frac{1}{2} \left( 4 + \frac{16}{4} \right) = 4 \)
- Since \( x_1 = x_0 \), the approximation stops here with \( \sqrt{16} = 4 \).
3. Estimation and Refinement
This method involves estimating the square root and then refining the estimate.
- Find two perfect squares between which the number lies.
- Estimate a value between these two square roots.
- Refine the estimate by averaging it with the division of the original number by the estimate.
- Repeat until the estimate is sufficiently accurate.
For example, to estimate \( \sqrt{20} \):
- \( 4^2 = 16 \) and \( 5^2 = 25 \), so \( \sqrt{20} \) is between 4 and 5.
- Initial estimate, \( x_0 = 4.5 \).
- Refinement, \( x_1 = \frac{1}{2} \left( 4.5 + \frac{20}{4.5} \right) \approx 4.47 \).
4. Using Exponentiation
On calculators without a dedicated square root function, use exponentiation:
- Enter the number you want the square root of.
- Raise it to the power of 0.5 (i.e., \( \sqrt{a} = a^{0.5} \)).
5. Continued Fractions
Continued fractions can provide an exact representation of square roots, though this method is more advanced and less practical for quick calculations.
These methods offer various ways to calculate square roots depending on the tools and precision required. Practicing these techniques can enhance your numerical proficiency and understanding of mathematical concepts.
Applications of Square Roots in Real Life
Square roots are a fundamental mathematical concept with a wide array of practical applications across various fields. Here are some of the key areas where square roots are utilized:
- Finance: In finance, square roots are used to calculate stock market volatility, which helps investors assess the risk of an investment. The standard deviation, a measure of market volatility, is derived from the square root of the variance of stock returns.
- Architecture and Engineering: Engineers use square roots to determine the natural frequency of structures, which is crucial for predicting how buildings and bridges will react to various forces such as wind and traffic. This ensures structural stability and safety.
- Physics: Square roots appear in many physical formulas, such as those calculating the velocity of an object, the intensity of sound waves, or the energy levels in quantum mechanics. These calculations help scientists understand and predict natural phenomena.
- Statistics: In statistics, the standard deviation, which measures data variability, is calculated using the square root of the variance. This helps statisticians analyze data sets and make informed decisions based on their findings.
- Geometry: The Pythagorean theorem, which involves square roots, is used to determine distances between points in space. This theorem is essential in fields such as navigation, surveying, and computer graphics.
- Computer Science: Square roots are used in algorithms for encryption, image processing, and game physics. For example, calculating the distance between points in a 3D space often involves square roots.
- Cryptography: Square roots play a role in cryptographic algorithms used for secure data transmission, digital signatures, and key exchange systems, ensuring the security and authenticity of communications.
- Navigation: Pilots and navigators use square roots to calculate the shortest distance between points on the earth's surface, aiding in accurate course plotting and efficient travel routes.
- Electrical Engineering: Calculations of power, voltage, and current in electrical circuits often involve square roots. These computations are critical for designing and maintaining efficient and safe electrical systems.
- Photography: The f-number, or aperture setting of a camera lens, is related to the square root of the lens's focal length. Adjusting the aperture affects the amount of light entering the camera, which is crucial for achieving the desired exposure in photographs.
These examples illustrate how square roots are not just abstract mathematical concepts but vital tools that help solve real-world problems in diverse disciplines.

Related Calculators and Tools
When working with square roots, especially in the context of a decimal to square root calculator, there are several related calculators and tools that can be incredibly helpful. These tools not only assist in calculating square roots but also provide solutions to various mathematical problems that are closely related to square roots.
1. Square Root Calculators
-
Mathway Square Root Calculator:
This calculator finds the square root of any given number, providing both exact and decimal forms for perfect and non-perfect squares respectively.
-
Omni Calculator:
Allows you to simplify square roots by breaking them into their prime factors, offering step-by-step solutions for better understanding.
-
Calculator Soup Square Root Calculator:
Offers functionality for finding both positive and negative square roots, and is useful for identifying perfect squares.
2. Perfect Square Calculators
-
Perfect Square Calculator by Calculator.net:
This tool determines whether a given number is a perfect square and provides both positive and negative square roots.
-
Good Calculators:
Includes a perfect square calculator that helps identify perfect squares and their corresponding roots efficiently.
3. Root and Radical Calculators
-
Easy Calculation Root Calculator:
Finds square roots of both integers and decimals, and offers a detailed step-by-step process for better comprehension.
-
Symbolab Root Calculator:
Calculates square roots along with other types of roots like cube roots, providing a versatile tool for various mathematical calculations.
4. Fractional Exponent Calculators
-
Calculator.net Fractional Exponents:
Helps in converting between radicals and fractional exponents, which is essential for advanced mathematical operations involving roots.
5. Practical Tools for Engineers and Scientists
-
Good Calculators Engineering Tools:
Includes various calculators such as the Resistor Color Code Calculator, Voltage Divider Calculator, and RMS Voltage Calculator, which are useful in practical applications involving square roots and other mathematical operations.
These calculators and tools provide comprehensive support for mathematical calculations involving square roots and related concepts, making complex problems easier to solve.
FAQs About Square Root Calculators
-
What is a square root calculator?
A square root calculator is a tool that finds the square root of any given non-negative number. It helps users quickly determine the square root of both perfect and non-perfect squares.
-
How does a square root calculator work?
The calculator uses the mathematical square root operation to calculate the root of a given number. This involves algorithms that approximate the square root to a high degree of accuracy.
-
Can a square root calculator handle decimals and fractions?
Yes, most square root calculators can handle both decimals and fractions. They can provide accurate results for square roots of non-integer values.
-
What is the square root of a negative number?
The square root of a negative number is an imaginary number. Square root calculators will typically display these roots using the imaginary unit \(i\), where \(i = \sqrt{-1}\).
-
How accurate are online square root calculators?
Online square root calculators are generally very accurate, providing results to several decimal places. However, the precision can vary depending on the specific calculator used.
-
Are there different methods for calculating square roots?
Yes, square roots can be calculated using several methods including prime factorization, estimation, and the long division method. Online calculators often use a combination of these techniques for accuracy.
-
What are the applications of square root calculators?
Square root calculators are used in various fields such as education, scientific research, engineering, and architecture. They are essential tools for solving problems involving quadratic equations, area calculations, and more.
-
Can square root calculators help with understanding mathematical concepts?
Absolutely! These calculators are great educational tools that help students grasp the concept of square roots and their properties, making learning math more interactive and enjoyable.
Tìm hiểu cách chuyển đổi số thập phân thành dạng căn bậc hai với video hướng dẫn chi tiết. Thu hút người xem bằng các bước dễ hiểu và chính xác.
Cách Chuyển Đổi Số Thập Phân Thành Dạng Căn Bậc Hai : Các Số Căn
READ MORE:
Khám phá cách tìm căn bậc hai của số thập phân với video được hơn một triệu lượt xem. Video hướng dẫn chi tiết và dễ hiểu giúp thu hút người xem.
Tìm Căn Bậc Hai Của Số Thập Phân - Hơn Một Triệu Lượt Xem