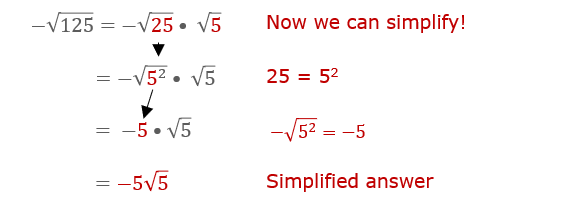Square Root Factoring Calculator: Simplify Your Math Problems Easily

A square root factoring calculator helps you find the factors of square roots and simplifies them for easier understanding and usage. Below are some functionalities and examples to illustrate its usage.

Calculator Use

This calculator can find the principal square root and roots of real numbers, both positive and negative. It can determine if a number is a perfect square and show the complex or imaginary solutions for square roots of negative numbers.

How to Use the Calculator

1. Enter the number you want to factor or find the square root of.
2. Press "Calculate" to get the factors and the simplified form of the square root.

Examples of Square Roots

• Square root of 81: \( \sqrt{81} = \pm 9 \)
• Square root of 25: \( \sqrt{25} = \pm 5 \)
• Square root of 100: \( \sqrt{100} = \pm 10 \)
• Square root of 10: \( \sqrt{10} = \pm 3.162278 \)

Factoring Square Roots

Here are some examples of factoring square roots:

• Factors of square root of 108: 2, 3, 3, 3
• Factors of square root of 64: 2, 2, 2, 2
• Factors of square root of 32: 2, 2, 2, 2, 2

Perfect Squares

A perfect square is a number that has an integer as its square root. For example:

• 4, because \( \sqrt{4} = 2 \)
• 9, because \( \sqrt{9} = 3 \)
• 16, because \( \sqrt{16} = 4 \)

Additional Resources

Square root factoring calculators are powerful tools used to simplify and solve mathematical expressions involving square roots. These calculators can handle a variety of calculations, from determining the square root of a number to factoring complex expressions into simpler components. They are designed to assist students, educators, and professionals in quickly finding accurate results without manual computation.

The primary function of a square root factoring calculator is to find the square root of a given number. For example, to find the square root of 81, the calculator will provide both positive and negative roots, \( \pm 9 \), since \( (-9)^2 = 81 \) and \( 9^2 = 81 \).

These calculators also help in identifying perfect squares and simplifying radical expressions. For instance, the square root of 25 is simplified to \( \pm 5 \), while the square root of 10 is approximately \( \pm 3.162 \). This is particularly useful in algebra and higher-level mathematics, where simplifying expressions can make solving equations more straightforward.

Additionally, square root factoring calculators can break down complex expressions into their factors. For example, the square root of 108 can be factored and simplified to \( 6\sqrt{3} \), making it easier to handle in further calculations.

Overall, square root factoring calculators are essential tools for anyone dealing with mathematical problems involving square roots, offering precise and quick solutions while simplifying complex expressions.

The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). This is represented as \( \sqrt{x} \). For example, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).

Square roots have several important properties:

• Every positive number has two square roots: one positive and one negative. For example, the square roots of 25 are 5 and -5.
• The principal square root of a number is the non-negative root, denoted as \( \sqrt{x} \).
• Square roots of negative numbers are complex and involve imaginary numbers. For instance, \( \sqrt{-1} = i \), where \( i \) is the imaginary unit.

Here are some key steps to understanding and working with square roots:

1. Identify Perfect Squares: Numbers like 4, 9, 16, and 25 are perfect squares because their square roots are integers. For instance, \( \sqrt{9} = 3 \).
2. Simplify Non-Perfect Squares: To simplify a square root, factor the number into a product of prime factors and group them into pairs. For example, to simplify \( \sqrt{18} \):
   1. Factor 18 into 9 and 2 (since \( 18 = 9 \times 2 \)).
   2. Simplify the square root of the perfect square: \( \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \).
3. Use of Square Root Calculators: These calculators can automatically simplify square roots and handle complex calculations involving roots. They are especially useful for large numbers or when dealing with imaginary roots.

Understanding square roots is fundamental in various areas of mathematics and practical applications, including geometry, algebra, and calculus.

Factoring is a fundamental concept in mathematics, used to simplify expressions and solve equations. It involves breaking down a complex expression into simpler components, or factors, that when multiplied together give the original expression. Here are the key concepts:

• Greatest Common Factor (GCF): The largest factor that two or more numbers have in common.
• Factoring by Grouping: A method used when an expression has four or more terms. The terms are grouped in pairs, and the GCF is factored out from each pair.
• Factoring Trinomials: Used for expressions of the form \(ax^2 + bx + c\). This can involve splitting the middle term or using the quadratic formula to find factors.
• Difference of Squares: Applies to expressions like \(a^2 - b^2\), which can be factored into \((a + b)(a - b)\).
• Perfect Square Trinomials: Forms like \(a^2 + 2ab + b^2\) that factor into \((a + b)^2\).
• Sum and Difference of Cubes: For expressions like \(a^3 + b^3\) or \(a^3 - b^3\), which factor into \((a + b)(a^2 - ab + b^2)\) and \((a - b)(a^2 + ab + b^2)\), respectively.

Understanding these basic concepts is essential for mastering more advanced mathematical topics and solving complex problems efficiently.

Square root calculators are essential tools for quickly determining the square root of a given number. These calculators are widely available online and can handle both positive and negative inputs. Here's a step-by-step guide on how to use them:

1. Input the Number: Enter the number for which you want to find the square root into the calculator. This can typically be done through a text box or a specific input field.
2. Submit the Input: Click the 'Calculate' or 'Submit' button. The calculator will process the input and provide the square root.
3. Review the Results: The results will show the principal square root. If the input is a perfect square, the answer will be an integer. For non-perfect squares, the calculator will display the result in both exact form (radical) and decimal approximation.
4. Additional Features: Many calculators offer additional functionalities, such as simplifying the radical form or providing complex roots for negative inputs.

Square root calculators are invaluable for students, engineers, and anyone needing to perform quick square root calculations. They save time and reduce the risk of manual errors.

Factoring techniques are essential for simplifying algebraic expressions and solving equations. Here are some common methods used in factoring:

• Trial Division
• Prime Factorization
• Greatest Common Factor (GCF)
• Factoring by Grouping
• Factoring Trinomials
• Difference of Squares
• Perfect Square Trinomials
• Sum and Difference of Cubes

Below is a detailed step-by-step guide for some of these techniques:

1. Trial Division:
   1. Find the square root of the integer number \( n \) and round down to the closest whole number. Let's call this number \( s \).
   2. Start with the number 1 and find the corresponding factor pair: \( n \div 1 = n \). So, 1 and \( n \) are a factor pair.
   3. Test all integers up through the square root \( s \) (i.e., \( n \div 2, n \div 3, \ldots, n \div s \)) to find other factor pairs where the division results in whole numbers with zero remainders.
   4. Record all factor pairs discovered in the previous step. These are the factors of \( n \).
2. Prime Factorization:
   1. Divide the number by the smallest prime number (2, 3, 5, etc.) until it no longer divides evenly.
   2. Continue the process with the quotient from the previous division, using the smallest prime numbers.
   3. Repeat until the quotient is 1. The prime factors are the divisors used in this process.
3. Greatest Common Factor (GCF):
   1. List the factors of each number.
   2. Identify the common factors between the numbers.
   3. The greatest common factor is the largest factor shared by the numbers.
4. Factoring by Grouping:
   1. Group terms in pairs that have a common factor.
   2. Factor out the common factor from each pair.
   3. If the remaining expressions share a common factor, factor that out as well.
5. Factoring Trinomials:
   1. For trinomials of the form \( ax^2 + bx + c \), find two numbers that multiply to \( ac \) and add to \( b \).
   2. Rewrite the middle term using these two numbers and factor by grouping.

Each of these techniques has specific applications and is useful in different scenarios for simplifying and solving algebraic problems.

In this section, we will explore several advanced techniques for factoring expressions, which are crucial for solving complex mathematical problems. These methods include factoring trinomials, the difference of squares, and factoring by grouping.

Factoring Trinomials

Factoring trinomials of the form \(ax^2 + bx + c\) involves finding two binomials that multiply to give the original trinomial. The steps are:

1. Identify the coefficients \(a\), \(b\), and \(c\).
2. Find two numbers that multiply to \(ac\) and add to \(b\).
3. Rewrite the middle term using the two numbers found.
4. Factor by grouping.

For example, to factor \(2x^2 + 5x + 3\), we look for two numbers that multiply to \(2 \cdot 3 = 6\) and add to 5. These numbers are 2 and 3. Rewrite as \(2x^2 + 2x + 3x + 3\), then factor by grouping: \(2x(x + 1) + 3(x + 1)\), resulting in \((2x + 3)(x + 1)\).

Difference of Squares

The difference of squares method is used for expressions of the form \(a^2 - b^2\). This can be factored into \((a + b)(a - b)\). For example:

\(x^2 - 9\) can be written as \(x^2 - 3^2\), which factors to \((x + 3)(x - 3)\).

Factoring by Grouping

Factoring by grouping is useful for polynomials with four or more terms. The steps are:

1. Group the terms into pairs.
2. Factor out the greatest common factor (GCF) from each pair.
3. Look for a common binomial factor.

For example, to factor \(x^3 + x^2 + x + 1\), group as \((x^3 + x^2) + (x + 1)\). Factor out the GCF: \(x^2(x + 1) + 1(x + 1)\). The common factor is \((x + 1)\), resulting in \((x^2 + 1)(x + 1)\).

Using these advanced factoring techniques, you can simplify complex expressions and solve a wide range of mathematical problems more efficiently.

Square root factoring is a valuable mathematical tool used in various fields. Below are some key applications:

1. Simplifying Radicals

Square root factoring is essential in simplifying radical expressions. By identifying the factors of a number and simplifying the square root, we can reduce complex expressions to their simplest form. This process is crucial in solving algebraic equations efficiently.

2. Solving Quadratic Equations

One common application is solving quadratic equations. By factoring the quadratic expression and applying the square root principle, we can find the solutions of the equation. This method is often more straightforward and quicker than using the quadratic formula.

3. Geometry and Measurement

In geometry, square root factoring is used to determine lengths and distances. For instance, in the Pythagorean theorem, the square root of the sum of the squares of the sides of a right triangle gives the length of the hypotenuse. Simplifying these square roots can make calculations more manageable.

4. Engineering and Physics

In engineering and physics, square root factoring is used to solve problems involving waves, oscillations, and other phenomena described by quadratic equations. For example, the natural frequency of a system can be found using square root factoring, which is crucial in designing stable structures and systems.

5. Computer Science

Algorithms often use square root factoring to optimize computations. For example, prime factorization algorithms leverage square root factoring to break down numbers efficiently. Additionally, it is used in graphics and cryptography for various calculations and transformations.

6. Financial Calculations

In finance, square root factoring is used to simplify calculations involving interest rates, annuities, and other financial instruments. By factoring out the square root, complex financial models can be simplified, making them easier to analyze and interpret.

Example Problems and Solutions

• Perfect Square Examples: Simplifying the square root of perfect squares such as 64, 81, and 100.
• Non-Perfect Square Examples: Approximating the square root of non-perfect squares like 50, 72, and 120.
• Complex Square Root Factoring: Simplifying expressions involving multiple radical terms.

Conclusion

Square root factoring is a fundamental tool with broad applications across various disciplines. Mastering this technique can greatly enhance problem-solving skills in mathematics, science, engineering, and beyond.

Understanding how to solve square root factoring problems requires practice with various types of equations. Below are some example problems and detailed solutions to illustrate the process.

Perfect Square Examples

• Example 1: Solve \( x^2 = 9 \).

  1. Recognize that this is a perfect square equation.
  2. Apply the square root property: \( x = \pm \sqrt{9} \).
  3. Simplify: \( x = \pm 3 \).
  4. So, the solutions are \( x = 3 \) and \( x = -3 \).

Non-Perfect Square Examples

• Example 2: Solve \( x^2 = 7 \).

  1. Recognize that this is not a perfect square equation.
  2. Apply the square root property: \( x = \pm \sqrt{7} \).
  3. Since \( \sqrt{7} \) cannot be simplified further, the solutions are \( x = \sqrt{7} \) and \( x = -\sqrt{7} \).

Complex Square Root Factoring

• Example 3: Solve \( x^2 - 4 = 0 \).

  1. Rewrite the equation: \( x^2 = 4 \).
  2. Apply the square root property: \( x = \pm \sqrt{4} \).
  3. Simplify: \( x = \pm 2 \).
  4. So, the solutions are \( x = 2 \) and \( x = -2 \).

• Example 4: Solve \( x^2 - 50 = 0 \).

  1. Isolate the quadratic term: \( x^2 = 50 \).
  2. Apply the square root property: \( x = \pm \sqrt{50} \).
  3. Simplify the radical: \( x = \pm 5\sqrt{2} \).
  4. So, the solutions are \( x = 5\sqrt{2} \) and \( x = -5\sqrt{2} \).

These examples highlight the step-by-step approach needed to solve various square root factoring problems. By practicing these techniques, you will improve your ability to tackle similar problems with confidence.

When working with square root factoring, having access to reliable calculator tools can greatly enhance efficiency and accuracy. Here are some of the most useful tools and resources available online:

• Symbolab Factoring Calculator:

  This tool allows you to factor complex expressions into simpler components. It supports a wide range of algebraic expressions including trinomials, polynomials, and more.

• Mathway Factoring Calculator:

  Mathway offers a comprehensive factoring calculator that can handle various types of expressions. It provides step-by-step solutions and is useful for learning and verifying your work.

• MathWarehouse Square Root Calculator:

  This calculator simplifies any square root to its simplest radical form and calculates the approximation of the root. It is particularly useful for checking your square root factoring work.

How to Use These Calculators

1. Enter the Expression: Input the algebraic expression or number into the calculator.
2. Select the Operation: Choose the appropriate operation such as factoring or square root calculation.
3. View the Results: The calculator will display the simplified form of the expression along with step-by-step explanations.

Additional Resources

• Worksheets and Practice Problems: Many of these calculators provide additional worksheets and problems to practice your skills.
• Tutorial Videos: Websites like Mathway and MathWarehouse often include tutorial videos that explain the concepts in detail.
• Mobile Apps: Downloadable apps for on-the-go calculations and learning. Both Symbolab and Mathway offer mobile versions of their calculators.

Here are some commonly asked questions about square root factoring calculators, along with detailed answers to help you understand their use and applications:

• What is a square root factoring calculator?

  A square root factoring calculator is a tool that helps you find the factors of a given number, especially those that are perfect squares. It simplifies the process of finding square roots and their factors, making complex calculations easier and faster.

• How do I use a square root factoring calculator?

  To use a square root factoring calculator, enter the number you want to factor into the input field. The calculator will then compute and display the square root along with its factors. Some advanced calculators may also provide step-by-step solutions.

• Can a square root factoring calculator handle non-perfect squares?

  Yes, many square root factoring calculators can handle non-perfect squares. They provide both the exact form and the decimal form of the square root, and list factors that are not whole numbers if necessary.

• What are the benefits of using a square root factoring calculator?

  Using a square root factoring calculator saves time and reduces the potential for errors in manual calculations. It is particularly useful for students, educators, and professionals who frequently work with square roots and factorizations in mathematics.

• Are there any online resources for learning more about square root factoring?

  Yes, there are numerous online resources available. Websites like Mathway, Symbolab, and Calculator Soup offer comprehensive guides, tutorials, and calculators to help you learn more about square root factoring and other mathematical concepts.

In this comprehensive guide, we have explored the fundamentals and applications of square root factoring calculators. These tools are invaluable for solving a variety of mathematical problems, from basic arithmetic to complex algebraic equations.

Square root factoring calculators simplify the process of finding square roots and factoring expressions, making it easier for students and professionals alike to perform accurate calculations quickly. Whether you are dealing with perfect squares or non-perfect squares, these calculators provide step-by-step solutions that enhance understanding and accuracy.

We have also discussed advanced factoring methods, including factoring trinomials, the difference of squares, and factoring by grouping. These techniques are crucial for solving higher-level mathematical problems and are greatly aided by the use of a reliable square root factoring calculator.

Additionally, we looked at various applications of square root factoring, demonstrating how these calculators can be used in real-world scenarios, from engineering to finance. The example problems and solutions provided in this guide serve as practical demonstrations of the calculator’s capabilities.

Numerous calculator tools and resources are available online, offering a wide range of functionalities. These resources are designed to cater to different needs, whether you are a beginner looking to understand the basics or an advanced user seeking sophisticated calculations.

Finally, the frequently asked questions section addressed common concerns and provided clear, concise answers to help users navigate the functionalities of square root factoring calculators. This ensures that users can maximize the potential of these tools in their mathematical endeavors.

In conclusion, square root factoring calculators are essential tools that streamline the calculation process, provide accurate results, and enhance overall mathematical comprehension. By leveraging these tools, users can tackle mathematical challenges with confidence and ease.