Topic simplified square root of 45: Welcome to our comprehensive guide on simplifying the square root of 45. Here, you will learn how to break down this non-perfect square into its simplest radical form, 3√5. We will explore prime factorization, mathematical steps, and real-life applications to deepen your understanding of this fundamental mathematical concept.
Table of Content
- Simplified Square Root of 45
- Understanding Square Roots
- Introduction to Square Root Simplification
- Prime Factorization Method
- Steps to Simplify the Square Root of 45
- Mathematical Explanation and Calculation
- Visual Representation of the Simplification Process
- Applications of Simplified Square Roots in Real Life
- Common Mistakes and How to Avoid Them
- Frequently Asked Questions (FAQs)
- Advanced Techniques for Simplifying Square Roots
- Conclusion and Summary
- YOUTUBE: Xem video 'Cách Đơn Giản Hóa Căn Thức của 45' để học cách đơn giản hóa căn bậc hai của 45 một cách dễ dàng và chính xác.
Simplified Square Root of 45
The square root of 45 can be simplified by finding its prime factorization and then grouping the prime factors in pairs. Here is the step-by-step process to simplify the square root of 45:
Prime Factorization
First, we find the prime factors of 45:
- 45 = 3 × 3 × 5
This means we can express 45 as \( 3^2 \times 5 \).
Simplifying the Square Root
We can simplify the square root of 45 using the prime factorization:
Since \( \sqrt{45} = \sqrt{3^2 \times 5} \), we can separate the square root into two parts:
\[
\sqrt{45} = \sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5}
\]
Now, we simplify the square root of \( 3^2 \):
\[
\sqrt{3^2} = 3
\]
Therefore, we have:
\[
\sqrt{45} = 3 \times \sqrt{5}
\]
So, the simplified form of \( \sqrt{45} \) is \( 3 \sqrt{5} \).
Final Simplified Form
The final simplified form of the square root of 45 is:
\[
\sqrt{45} = 3 \sqrt{5}
\]
Thus, when simplified, the square root of 45 is \( 3 \sqrt{5} \).

READ MORE:
Understanding Square Roots
Square roots are mathematical functions that determine a value which, when multiplied by itself, yields the original number. For instance, the square root of 9 is 3 because 3 multiplied by 3 equals 9. This concept can be expressed as √9 = 3.
Mathematically, square roots are represented by the radical symbol (√). The number under the radical is called the radicand. For example, in √45, the radicand is 45.
Square roots can be categorized into two types:
- Perfect Square Roots: These are square roots of perfect squares, such as 4, 9, 16, etc. For example, √16 = 4 because 4 × 4 = 16.
- Non-Perfect Square Roots: These are square roots of numbers that are not perfect squares, like 2, 3, 5, etc. Their square roots are often irrational numbers, meaning their decimal forms are non-repeating and non-terminating. For example, √2 ≈ 1.414.
The process of finding square roots can involve methods such as prime factorization, estimation, and using calculators for more complex numbers. Understanding square roots is fundamental for various mathematical concepts and real-life applications, such as geometry, physics, and engineering.
Using prime factorization, we can simplify square roots to their simplest form. For example, to simplify √45, we find its prime factors:
- 45 = 9 × 5
- √45 = √(9 × 5)
- √45 = √9 × √5
- Since √9 = 3, we get 3√5
Thus, the simplified form of √45 is 3√5.
Understanding these basics helps in further exploration of algebraic expressions and advanced mathematics.
Introduction to Square Root Simplification
Square root simplification is a process used to make a square root expression as simple as possible. Simplifying square roots involves breaking down the number inside the square root into its prime factors and then reducing the expression by taking out any perfect squares. This makes the expression easier to work with and understand.
Let's explore how to simplify the square root of 45 using a step-by-step approach:
Steps to Simplify the Square Root of 45
- Prime Factorization: Find the prime factors of 45. The prime factors of 45 are 3 and 5, since 45 can be written as 32 × 5.
- Rewrite the Expression: Express 45 under the square root as the product of its prime factors:
\[\sqrt{45} = \sqrt{3^2 \times 5}\]
- Separate the Square Root: Use the property of square roots that \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):
\[\sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5}\]
- Simplify the Perfect Square: The square root of 32 is 3:
\[\sqrt{3^2} = 3\]
- Combine the Results: Multiply the simplified square root of the perfect square by the remaining square root:
\[3 \times \sqrt{5} = 3\sqrt{5}\]
Therefore, the simplified form of the square root of 45 is 3√5.
Why Simplify Square Roots?
- Simplification: Simplified square roots are easier to work with in mathematical calculations and algebraic expressions.
- Clarity: Simplified expressions are often clearer and more concise, making it easier to understand the underlying mathematics.
- Applications: Simplified square roots are frequently used in geometry, physics, engineering, and other fields where precise calculations are necessary.
Prime Factorization Method
The prime factorization method is a systematic way of finding the square root of a number by breaking it down into its prime factors. Here is a step-by-step guide on how to simplify the square root of 45 using this method:
- Find the Prime Factors:
First, identify the prime factors of 45. Prime factors are the prime numbers that multiply together to give the original number. For 45, the prime factors are:
\[
45 = 3 \times 3 \times 5 = 3^2 \times 5
\] - Group the Factors:
Next, group the prime factors into pairs of the same number. For 45, we have one pair of 3's:
\[
45 = 3^2 \times 5
\] - Take One Factor from Each Pair:
For each pair of identical factors, take one factor out of the square root. For the factor 3, since it appears twice, we take one 3 out of the square root:
\[
\sqrt{45} = \sqrt{3^2 \times 5} = 3 \sqrt{5}
\] - Simplify the Expression:
The simplified form of the square root of 45 is:
\[
\sqrt{45} = 3 \sqrt{5}
\]
By using the prime factorization method, we have successfully simplified the square root of 45 to \(3 \sqrt{5}\). This method is efficient and helps in understanding the fundamental process of breaking down numbers into their prime factors and simplifying square roots.
Steps to Simplify the Square Root of 45
Simplifying the square root of 45 involves breaking it down into its prime factors and then applying the rules of square roots. Follow these steps:
-
Factorize 45 into its prime factors:
45 = 3 × 3 × 5
-
Rewrite the square root of 45 using these prime factors:
\[\sqrt{45} = \sqrt{3 \times 3 \times 5}\]
-
Group the pairs of prime factors under the square root:
\[\sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5}\]
-
Simplify the square roots of the pairs:
\[\sqrt{3^2} = 3\]
-
Combine the simplified square roots:
\[\sqrt{45} = 3\sqrt{5}\]
Thus, the simplified form of the square root of 45 is:
\[\sqrt{45} = 3\sqrt{5}\]
Breaking down the steps:
- Prime Factorization: Identify the prime factors of 45 which are 3 and 5. 45 can be written as \(3^2 \times 5\).
- Applying Square Root Rules: Use the rule \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) to separate the factors under the square root.
- Extracting Perfect Squares: The perfect square \(3^2\) can be taken out of the square root as 3.
Through these steps, you can see how the square root of 45 is simplified to \(3\sqrt{5}\), which is the most reduced form.
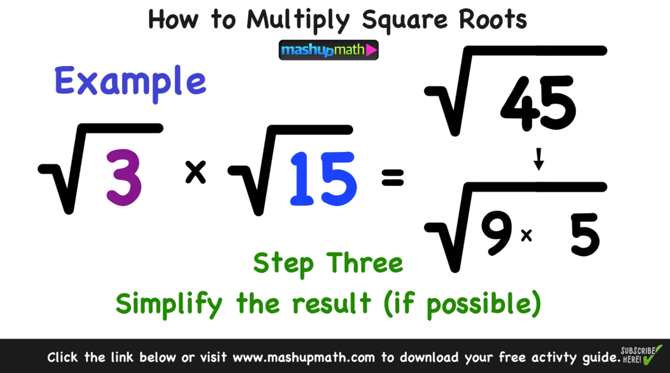
Mathematical Explanation and Calculation
To understand the mathematical explanation and calculation for simplifying the square root of 45, we will break it down step by step using the prime factorization method.
-
First, let's write the number 45 as a product of its prime factors:
45 = 3 × 3 × 5
-
Next, express the prime factors under the square root:
\(\sqrt{45} = \sqrt{3^2 \times 5}\)
-
According to the properties of square roots, we can separate the factors inside the square root:
\(\sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5}\)
-
Simplify \(\sqrt{3^2}\), which is 3, since the square root of a square number is the number itself:
\(\sqrt{3^2} = 3\)
-
Therefore, we get:
\(\sqrt{45} = 3 \times \sqrt{5}\)
So, the simplified form of \(\sqrt{45}\) is \(3\sqrt{5}\).
For a deeper understanding, let's consider the decimal approximation of the square root of 45:
Using a calculator, \(\sqrt{45} \approx 6.708\). This approximation can be useful in practical applications where an exact square root is not required.
Finally, it's important to note that \(\sqrt{45}\) is an irrational number. An irrational number is one that cannot be expressed as a fraction of two integers, and its decimal representation is non-repeating and non-terminating.
Visual Representation of the Simplification Process
Simplifying the square root of 45 can be visually represented step-by-step, illustrating the transformation of the expression into its simplest form.
Let's start by breaking down the number inside the square root into its prime factors:
- The number 45 can be expressed as the product of 9 and 5: \(45 = 9 \times 5\).
- Using the property of square roots, we can separate the factors: \(\sqrt{45} = \sqrt{9 \times 5}\).
- Next, we apply the rule \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\): \(\sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5}\).
- Since the square root of 9 is 3, we simplify the expression: \(\sqrt{9} \times \sqrt{5} = 3\sqrt{5}\).
Therefore, the simplified form of \(\sqrt{45}\) is \(3\sqrt{5}\).
Step-by-Step Visual Explanation
-
Prime Factorization:
\(45\) = \(9 \times 5\) -
Applying the Square Root Property:
\(\sqrt{45}\) = \(\sqrt{9 \times 5}\) -
Separating the Factors:
\(\sqrt{9 \times 5}\) = \(\sqrt{9} \times \sqrt{5}\) -
Simplifying the Square Root of 9:
\(\sqrt{9}\) = 3 -
Final Simplified Form:
\(\sqrt{45}\) = \(3\sqrt{5}\)
To further illustrate the simplification process, here's a visual diagram:
| \(45\) | \(\rightarrow\) | \(9 \times 5\) | \(\rightarrow\) | \(\sqrt{9 \times 5}\) | \(\rightarrow\) | \(\sqrt{9} \times \sqrt{5}\) | \(\rightarrow\) | \(3\sqrt{5}\) |
This table summarizes the steps from the original number to its simplest square root form.
By understanding and visualizing each step, the simplification of square roots becomes a more intuitive and manageable process.
Applications of Simplified Square Roots in Real Life
Simplified square roots have various practical applications in real-life situations across different fields. Here are some key examples:
-
Finance:
In finance, square roots are used to calculate stock market volatility, which measures how much a stock’s price fluctuates over time. This is crucial for assessing the risk of investments. The formula for calculating the standard deviation, a measure of volatility, involves the square root of the variance of stock returns.
-
Architecture and Engineering:
Square roots are used to determine the natural frequencies of structures like buildings and bridges. This helps in designing structures that can withstand different loads and stresses. For example, the Pythagorean theorem, which involves square roots, is used to calculate distances and dimensions in construction projects.
-
Science and Physics:
In science, square roots are used in various calculations, such as determining the intensity of sound waves, the amount of radiation absorbed by materials, and the velocity of moving objects. These calculations are essential for scientific research and technological development.
-
Statistics:
Square roots are fundamental in statistics for calculating standard deviation and variance. These measures are crucial for data analysis, helping statisticians understand the spread and distribution of data sets.
-
Geometry:
In geometry, square roots are used to calculate the area and perimeter of shapes, particularly when dealing with right triangles. The Pythagorean theorem, which uses square roots, helps find the lengths of sides in right triangles, aiding in various geometric calculations.
-
Computer Science:
In computer science, square roots are used in algorithms for encryption, image processing, and game physics. For instance, encryption algorithms often use square roots to generate keys for securing data.
-
Navigation:
In navigation, square roots are used to compute distances between points on maps. This is essential for planning routes and estimating travel times. The distance formula, which involves square roots, helps in calculating the shortest path between two points.
-
Electrical Engineering:
Square roots are used in electrical engineering to calculate power, voltage, and current in circuits. These calculations are crucial for designing and optimizing electrical systems and devices.
-
Cooking:
In cooking, square roots can be used to adjust recipe quantities. For example, when scaling a recipe up or down, using the square root of the scaling factor helps maintain the correct proportions of ingredients, ensuring the desired taste and texture.
Overall, the use of simplified square roots in these applications highlights their importance in solving real-world problems efficiently and accurately.
Common Mistakes and How to Avoid Them
When simplifying square roots, it's easy to make mistakes. Here are some common errors and tips on how to avoid them:
-
Incorrect Factorization:
One common mistake is to incorrectly factorize the number under the square root. Ensure you break down the number into its correct prime factors.
- Example: For \( \sqrt{45} \), correctly factorize 45 as \( 9 \times 5 \).
- Check: Verify the factorization by multiplying the factors back together to get the original number.
-
Forgetting to Simplify Completely:
Sometimes, people stop simplifying too early. Make sure to simplify until all possible factors are out of the square root.
- Example: \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \).
-
Incorrect Application of Square Root Properties:
Applying properties of square roots incorrectly can lead to errors. Remember the rule \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Example: Simplify \( \sqrt{50} \) correctly by recognizing that \( 50 = 25 \times 2 \).
- Correct Calculation: \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \).
-
Confusing Addition and Multiplication:
Remember that you cannot add square roots directly unless they are like terms.
- Example: \( \sqrt{45} + \sqrt{20} \) is not equal to \( \sqrt{65} \). Simplify each term separately: \( 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5} \).
-
Not Checking Your Work:
Always recheck your steps to ensure accuracy.
- Tip: Substitute your simplified result back to see if it matches the original square root's decimal value.
By avoiding these common mistakes, you can ensure that your process of simplifying square roots is accurate and efficient.

Frequently Asked Questions (FAQs)
-
What is the square root of 45?
The square root of 45 is approximately 6.708. In its simplified radical form, it is expressed as \(3\sqrt{5}\).
-
How do you simplify the square root of 45?
To simplify \(\sqrt{45}\), follow these steps:
- Express 45 as a product of its prime factors: \(45 = 3 \times 3 \times 5\).
- Rewrite the expression as \(\sqrt{3 \times 3 \times 5}\).
- Since \(\sqrt{3 \times 3} = 3\), pull this term out of the square root: \(3\sqrt{5}\).
Thus, the simplified form of \(\sqrt{45}\) is \(3\sqrt{5}\).
-
Is the square root of 45 a rational number?
No, the square root of 45 is not a rational number. It is an irrational number because it cannot be expressed as a simple fraction.
-
How is the square root of 45 used in real life?
The square root of 45, like other square roots, can be used in various fields such as engineering, physics, and architecture, where precise measurements and calculations are necessary. For example, it can be used to calculate distances, areas, and in solving quadratic equations.
-
Can you find the square root of 45 using the long division method?
Yes, the square root of 45 can be found using the long division method, which provides a way to calculate it to several decimal places. The process involves dividing 45 into successive pairs of digits, determining an approximate quotient, and iteratively refining this quotient until the desired precision is achieved.
-
Why is 45 not a perfect square?
A number is a perfect square if its square root is an integer. Since the square root of 45 is approximately 6.708 and not an integer, 45 is not a perfect square.
Advanced Techniques for Simplifying Square Roots
Simplifying square roots can often involve more advanced techniques that go beyond basic factorization. Here are some methods to enhance your skills in this area:
- Using the Quotient Property: This property states that the square root of a quotient is equal to the quotient of the square roots. For example:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
This method is particularly useful when dealing with fractions under the radical.
- Product Property: This property helps in breaking down complex radicands into simpler parts. It states:
\(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\)
Using this, you can simplify expressions like \(\sqrt{50}\) into \(\sqrt{25 \times 2} = 5\sqrt{2}\).
- Prime Factorization: Breaking down the radicand into its prime factors can significantly simplify the process. For instance:
\(\sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{2^2 \times 2 \times 3^2} = 6\sqrt{2}\)
- Simplifying with Variables: When simplifying square roots that include variables, apply the same principles:
For example, \(\sqrt{x^4 y^2} = x^2 y\), since both \(x^4\) and \(y^2\) are perfect squares.
- Combining Like Terms: In some cases, after simplification, like terms can be combined. For example:
\(\sqrt{45} + \sqrt{20} = 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5}\)
- Rationalizing the Denominator: When a square root appears in the denominator, it is often rationalized:
For example, \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\).
By mastering these techniques, you can handle a wide variety of square root problems with greater ease and confidence.
Conclusion and Summary
The square root of 45, simplified as \( \sqrt{45} = 3\sqrt{5} \), illustrates an important aspect of irrational numbers. Since 45 is not a perfect square, its square root cannot be expressed as a simple fraction, making it an irrational number. This results in a non-repeating, non-terminating decimal expansion of approximately 6.708.
Throughout this guide, we have explored various methods to simplify square roots, specifically focusing on the prime factorization method to simplify \( \sqrt{45} \) as \( 3\sqrt{5} \). We also touched upon the long division method to find its decimal approximation.
The simplified form \( 3\sqrt{5} \) is not just a mathematical curiosity but has practical applications in solving real-life problems, such as calculating dimensions in geometric problems and converting measurements in various fields. Understanding the properties and simplification of square roots can significantly enhance problem-solving skills and mathematical reasoning.
In summary, the key takeaways are:
- The square root of 45 can be simplified to \( 3\sqrt{5} \).
- This simplified form helps in making complex calculations more manageable.
- The decimal approximation of \( \sqrt{45} \) is approximately 6.708, reflecting its nature as an irrational number.
By mastering these concepts, you can handle a variety of mathematical challenges with greater ease and confidence.
Xem video 'Cách Đơn Giản Hóa Căn Thức của 45' để học cách đơn giản hóa căn bậc hai của 45 một cách dễ dàng và chính xác.
Cách Đơn Giản Hóa Căn Thức của 45
READ MORE:
Xem video 'Đơn Giản Hóa Căn Bậc Hai của 45' để học cách đơn giản hóa căn bậc hai của 45 một cách dễ dàng và chính xác.
Đơn Giản Hóa Căn Bậc Hai của 45











