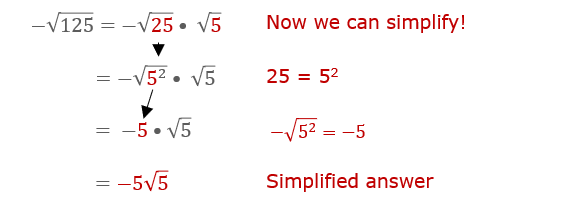Topic simplify a square root calculator: Discover the easiest way to simplify square roots using our comprehensive calculator. This guide will walk you through step-by-step instructions, helpful tips, and practical examples to ensure you master the art of simplifying square roots effortlessly. Whether you're a student or just brushing up on your math skills, this tool is designed to make your life easier.
Table of Content
- Simplify a Square Root Calculator
- Introduction to Simplifying Square Roots
- Understanding Square Roots
- Basic Properties of Square Roots
- Step-by-Step Guide to Simplifying Square Roots
- Prime Factorization Method
- Examples of Simplifying Square Roots
- Simplifying Square Roots in Fractions
- Using Square Root Calculators
- Common Mistakes and How to Avoid Them
- Advanced Techniques for Simplifying Square Roots
- Applications of Square Roots in Various Fields
- Conclusion and Further Resources
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai bằng máy tính đồ thị, phù hợp cho người học toán.
Simplify a Square Root Calculator
This calculator helps you to simplify square roots to their simplest form. It provides step-by-step instructions for breaking down a square root into its prime factors, extracting perfect squares, and simplifying the expression.
How to Use the Square Root Simplifier
- Enter the radicand (the number under the square root) into the input box.
- Click the "Simplify" button to see the step-by-step solution and the simplified form of the square root.
- The calculator will display whether the number is a perfect square or not, and provide the simplified form in exact and decimal formats if applicable.
Example Calculations
- The square root of 8: $$ \sqrt{8} = \sqrt{4 \times 2} = \sqrt{2^2 \times 2} = 2\sqrt{2} \approx 2.828 $$
- The square root of 12: $$ \sqrt{12} = \sqrt{4 \times 3} = \sqrt{2^2 \times 3} = 2\sqrt{3} \approx 3.464 $$
- The square root of 20: $$ \sqrt{20} = \sqrt{4 \times 5} = \sqrt{2^2 \times 5} = 2\sqrt{5} \approx 4.472 $$
Properties of Square Roots
- Product Property: $$ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} $$
- Quotient Property: $$ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} $$
- Simplifying a Square Root: $$ \sqrt{n} = \sqrt{a^2 \times b} = a\sqrt{b} $$
Why Calculate Square Roots?
Square roots are essential in various areas of mathematics, including algebra, geometry, and solving polynomial equations. They are also used to simplify expressions involving radicals and to solve problems related to the Pythagorean theorem.
Steps for Simplifying Square Roots
- Identify the radicand and check for perfect square factors.
- Factorize the radicand into its prime factors.
- Extract the square root of any perfect square factors.
- Simplify the remaining expression under the square root.

READ MORE:
Introduction to Simplifying Square Roots
Understanding how to simplify square roots is a fundamental skill in mathematics. Simplifying a square root involves breaking down the radicand (the number under the square root) into its prime factors and then simplifying those factors. This process can make complex calculations easier and more intuitive. Let's explore the step-by-step method to simplify square roots effectively.
- Step 1: Prime Factorization
Begin by finding the prime factorization of the radicand. For example, the number 18 can be factorized into 2 x 3 x 3.
- Step 2: Grouping Factors
Group the prime factors into pairs. Each pair of identical factors can be taken out of the square root. For example, √18 = √(2 x 3 x 3) = √(3 x 3) x √2 = 3√2.
- Step 3: Simplifying the Expression
Multiply the numbers outside the square root and simplify the expression. Using the previous example, the simplified form of √18 is 3√2.
- Special Cases
Some square roots may involve more complex numbers, including fractions or larger numbers, requiring additional steps but following the same principles of factorization and pairing.
By mastering these steps, you can simplify any square root, making your calculations more straightforward and efficient.
Understanding Square Roots
Square roots are fundamental in mathematics, representing a value that, when multiplied by itself, yields the original number. Simplifying square roots can make complex calculations easier and more intuitive. Let's delve into the basics and understand the properties and methods used to simplify square roots.
- Definition of Square Root: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \).
- Properties of Square Roots:
- \( \sqrt{x \cdot y} = \sqrt{x} \cdot \sqrt{y} \)
- \( \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}} \)
- \( (\sqrt{x})^2 = x \)
- Prime Factorization Method:
- Identify the prime factors of the number under the square root (radicand).
- Group the prime factors into pairs.
- Move one factor of each pair outside the square root.
- Multiply the factors outside the square root to get the simplified form.
Example: Simplify \( \sqrt{72} \)
- Prime factors of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Group into pairs: \( (2 \times 2) \) and \( (3 \times 3) \)
- Move one factor outside: \( 2 \times 3 = 6 \)
- Result: \( \sqrt{72} = 6\sqrt{2} \)
- Using Calculator:
Many online calculators can simplify square roots by following the steps mentioned. Enter the radicand and the calculator will provide the simplified form along with the step-by-step solution.
Basic Properties of Square Roots
Square roots are fundamental mathematical operations with several essential properties. Understanding these properties can help simplify expressions and solve equations involving square roots. Below are the basic properties and rules:
-
Definition:
The square root of a number \(x\) is a number \(a\) such that \(a^2 = x\). This is denoted as \(\sqrt{x}\).
-
Principal Square Root:
The principal square root is the non-negative square root of a non-negative number. For example, the principal square root of 9 is 3, denoted as \(\sqrt{9} = 3\).
-
Properties:
-
Product Property:
\(\sqrt{x \cdot y} = \sqrt{x} \cdot \sqrt{y}\)
-
Quotient Property:
\(\sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}}\)
-
Power of a Square Root:
\(\sqrt{x^2} = |x|\)
-
Product Property:
-
Perfect Squares:
If \(x\) is a perfect square, then \(\sqrt{x}\) is an integer. For example, \( \sqrt{16} = 4 \) because \( 4^2 = 16 \).
-
Simplifying Square Roots:
To simplify a square root, factor the radicand (the number under the square root) into its prime factors and then apply the product property. For example:
\(\sqrt{72} = \sqrt{2^3 \cdot 3^2} = \sqrt{2^2 \cdot 2 \cdot 3^2} = 2 \cdot 3 \cdot \sqrt{2} = 6\sqrt{2}\)
Step-by-Step Guide to Simplifying Square Roots
Simplifying square roots involves breaking down the radicand into its prime factors and then grouping and extracting perfect squares. Follow these detailed steps to simplify any square root:
- Identify the radicand and factorize it into its prime factors.
- Group the prime factors into pairs of identical factors.
- Extract each pair of identical factors from under the square root.
- Multiply the numbers extracted from the square root.
- Combine the extracted numbers with the remaining factors under the square root.
Example: To simplify √72, start by factorizing 72 into prime factors: 72 = 2 × 2 × 2 × 3 × 3.
In the example, group the factors: 72 = (2 × 2) × (2) × (3 × 3).
For each pair, one number comes out of the square root. Example: √(2 × 2) × (2) × √(3 × 3) becomes 2 × 3 × √2.
Continuing the example: 2 × 3 = 6.
Final result: √72 = 6√2.
This method ensures that the square root is simplified to its simplest form, making it easier to work with in further calculations.

Prime Factorization Method
The prime factorization method is a systematic approach to simplifying square roots by breaking down the radicand into its prime factors. Here’s how to do it step-by-step:
- Identify the radicand (the number under the square root symbol).
- Find the prime factorization of the radicand. This means expressing the number as a product of its prime factors.
- Group the prime factors in pairs. Each pair of identical factors can be taken out of the square root.
- Multiply the factors outside the square root together. The remaining factors inside the square root are multiplied together as well.
Let's go through an example to understand this better:
Example: Simplify √72.
- Step 1: Identify the radicand: 72.
- Step 2: Find the prime factorization of 72: 72 = 2 × 2 × 2 × 3 × 3.
- Step 3: Group the prime factors in pairs: (2 × 2) × (3 × 3) × 2.
- Step 4: Take one factor from each pair outside the square root: 2 × 3.
- Step 5: Multiply the factors outside the square root: 2 × 3 = 6.
- Step 6: The remaining factor inside the square root is 2. So, √72 = 6√2.
Using this method helps in simplifying complex square roots efficiently and accurately.
Examples of Simplifying Square Roots
Understanding how to simplify square roots involves recognizing perfect squares and their factors. Below are detailed examples that illustrate the step-by-step process of simplifying square roots.
Example 1: Simplify √12
To simplify √12, follow these steps:
- Identify factors of 12: \( 12 = 4 \times 3 \).
- Rewrite the square root: \( \sqrt{12} = \sqrt{4 \times 3} \).
- Separate the square root: \( \sqrt{4} \times \sqrt{3} \).
- Simplify the square root of 4: \( 2 \sqrt{3} \).
Example 2: Simplify √45
To simplify √45, follow these steps:
- Identify factors of 45: \( 45 = 9 \times 5 \).
- Rewrite the square root: \( \sqrt{45} = \sqrt{9 \times 5} \).
- Separate the square root: \( \sqrt{9} \times \sqrt{5} \).
- Simplify the square root of 9: \( 3 \sqrt{5} \).
Example 3: Simplify √18
To simplify √18, follow these steps:
- Identify factors of 18: \( 18 = 9 \times 2 \).
- Rewrite the square root: \( \sqrt{18} = \sqrt{9 \times 2} \).
- Separate the square root: \( \sqrt{9} \times \sqrt{2} \).
- Simplify the square root of 9: \( 3 \sqrt{2} \).
Example 4: Simplify √8
To simplify √8, follow these steps:
- Identify factors of 8: \( 8 = 4 \times 2 \).
- Rewrite the square root: \( \sqrt{8} = \sqrt{4 \times 2} \).
- Separate the square root: \( \sqrt{4} \times \sqrt{2} \).
- Simplify the square root of 4: \( 2 \sqrt{2} \).
Example 5: Simplify 2√12 + 9√3
To simplify 2√12 + 9√3, follow these steps:
- Simplify \( 2 \sqrt{12} \): \( 2 \times 2 \sqrt{3} = 4 \sqrt{3} \).
- Combine like terms: \( 4 \sqrt{3} + 9 \sqrt{3} = (4 + 9) \sqrt{3} = 13 \sqrt{3} \).
Example 6: Simplify √20 × √5√2
To simplify √20 × √5√2, follow these steps:
- Combine the radicals: \( \sqrt{20} \times \sqrt{5} \times \sqrt{2} \).
- Simplify inside the square root: \( \sqrt{20 \times 5 \times 2} = \sqrt{200} \).
- Factorize 200: \( 200 = 100 \times 2 \).
- Simplify the square root: \( \sqrt{100 \times 2} = 10 \sqrt{2} \).
These examples demonstrate the process of simplifying square roots by breaking down the radicand into its prime factors, identifying perfect squares, and pulling them out of the square root for a simplified expression.
Simplifying Square Roots in Fractions
Simplifying square roots in fractions can be a bit challenging, but with a step-by-step approach, it becomes manageable. Here's how you can simplify square roots in fractions:
-
Identify the Fraction: Start with a fraction where both the numerator and the denominator are square roots. For example,
\(\frac{\sqrt{a}}{\sqrt{b}}\). -
Combine the Radicals: Use the property of square roots that allows you to combine them under a single radical. This property states that
\(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\).For example,
\(\frac{\sqrt{8}}{\sqrt{2}} = \sqrt{\frac{8}{2}} = \sqrt{4}\). -
Simplify the Radicand: Simplify the expression inside the square root if possible. In the example above,
\(\sqrt{4}\)simplifies to 2. -
Rationalize the Denominator (if necessary): If the fraction has a square root in the denominator, multiply the numerator and the denominator by the same square root to eliminate the square root from the denominator. For example,
\(\frac{1}{\sqrt{2}}\)can be rationalized by multiplying by\(\frac{\sqrt{2}}{\sqrt{2}}\)to get\(\frac{\sqrt{2}}{2}\). -
Final Simplification: Ensure the final expression is in its simplest form. Combine any like terms or further simplify if necessary.
Here are a few examples to illustrate these steps:
- Example 1: Simplify
\(\frac{\sqrt{50}}{\sqrt{2}}\)- Combine the radicals:
\(\frac{\sqrt{50}}{\sqrt{2}} = \sqrt{\frac{50}{2}} = \sqrt{25}\) - Simplify the radicand:
\(\sqrt{25} = 5\) - Final result: 5
- Combine the radicals:
- Example 2: Simplify
\(\frac{3}{\sqrt{5}}\)- Rationalize the denominator:
\(\frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5}\) - Final result:
\(\frac{3\sqrt{5}}{5}\)
- Rationalize the denominator:
- Example 3: Simplify
\(\frac{\sqrt{18}}{\sqrt{2}}\)- Combine the radicals:
\(\frac{\sqrt{18}}{\sqrt{2}} = \sqrt{\frac{18}{2}} = \sqrt{9}\) - Simplify the radicand:
\(\sqrt{9} = 3\) - Final result: 3
- Combine the radicals:
By following these steps, you can simplify square roots in fractions effectively and accurately. Practice with different examples to become more comfortable with the process.
Using Square Root Calculators
Square root calculators are valuable tools that help simplify the process of finding the square root of a number, especially when dealing with complex or large numbers. Here's a step-by-step guide on how to use these calculators effectively:
- Access the Calculator:
Visit a reliable square root calculator online. Some popular options include Mathway, Symbolab, and MathCracker.
- Enter the Radicand:
Input the number or expression under the square root (the radicand) into the provided input field. For instance, if you need to simplify √24, you would enter 24.
- Choose the Operation:
Select the appropriate operation if required. Some calculators might offer additional functions like simplifying, calculating, or showing steps. For simplification, ensure you select the 'Simplify' or equivalent option.
- Calculate:
Click the 'Calculate' or 'Simplify' button. The calculator will process the input and display the result.
- Review the Steps:
Most advanced calculators will provide a step-by-step breakdown of the simplification process. This can help you understand the method and learn how to perform similar calculations manually.
Here's an example to illustrate:
- Example: Simplifying √24
- Input 24 into the calculator.
- The calculator identifies the prime factorization of 24, which is 23 * 3.
- It then simplifies the expression: √24 = √(23 * 3) = √(22 * 2 * 3) = 2√6.
- The result, 2√6, is displayed along with the steps.
Square root calculators can also handle more complex expressions, including fractions and decimals, providing both exact and decimal forms of the results.
Some additional features of advanced square root calculators include:
- Handling fractional radicands and providing simplified forms.
- Offering detailed explanations and steps for each calculation.
- Allowing for the input of complex expressions involving multiple square roots and arithmetic operations.
By using these calculators, you can save time and ensure accuracy in your calculations, making them an essential tool for students, teachers, and anyone dealing with mathematical problems involving square roots.

Common Mistakes and How to Avoid Them
Simplifying square roots can be challenging, and students often make common mistakes. Here are some frequent errors and tips to avoid them:
- Forgetting to Check for Perfect Squares:
One common mistake is not identifying perfect squares within the radicand (the number inside the square root). Always look for factors that are perfect squares.
- Incorrectly Applying Properties of Exponents and Radicals:
Students may forget to distribute exponents correctly or mix up rules for multiplying and dividing square roots. It’s essential to review and understand these properties.
- (Correct)
- (Correct)
- Rushing the Simplification Process:
Hurrying through simplification can lead to errors. Take your time to work through each step methodically.
- Failing to Recognize Remaining Factors:
After an initial simplification, there may still be factors that can be simplified further. Double-check your work to ensure all possible simplifications are made.
- Misapplying Rules to Complex Expressions:
When dealing with complex expressions involving square roots, carefully apply appropriate simplification techniques and avoid making errors while manipulating the expressions.
To avoid these mistakes, consider the following strategies:
- Practice Regularly: Consistent practice helps reinforce correct techniques and builds confidence.
- Seek Help When Needed: Utilize online resources, math tutors, or teachers to get assistance and different perspectives on challenging concepts.
- Double-Check Calculations: Always review your steps and final answers to catch any errors.
By being aware of these common mistakes and implementing strategies to avoid them, students can improve their skills in simplifying square roots.
Advanced Techniques for Simplifying Square Roots
Simplifying square roots can go beyond basic methods. Here are some advanced techniques to help you master the process:
-
Prime Factorization
Start by expressing the radicand as a product of its prime factors. For example, to simplify √72, first find its prime factors:
\[72 = 2^3 \times 3^2\]
Group the prime factors into pairs:
\[√72 = √(2^3 \times 3^2) = √(2^2 \times 3^2 \times 2) = 2 \times 3 \times √2 = 6√2\]
-
Using Exponent Rules
Another method involves using exponent rules. Recall that:
\[√x = x^{1/2}\]
This can help simplify expressions involving roots and exponents:
\[√(a \times b) = √a \times √b\]
For example:
\[√50 = √(25 \times 2) = √25 \times √2 = 5√2\]
-
Rationalizing the Denominator
When dealing with fractions, it's often necessary to rationalize the denominator. This means eliminating any square roots from the denominator:
For example:
\[\frac{1}{√2}\]
Multiply the numerator and the denominator by √2:
\[\frac{1}{√2} \times \frac{√2}{√2} = \frac{√2}{2}\]
-
Higher Order Roots
Simplifying higher-order roots (like cube roots) involves finding perfect cube factors:
For example, to simplify ∛54:
\[54 = 2 \times 3^3\]
So:
\[∛54 = ∛(3^3 \times 2) = 3∛2\]
-
Combining Radicals
For expressions involving multiple radicals, use the properties of radicals to combine them:
\[\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}\]
For example:
\[\sqrt{3} \times \sqrt{12} = \sqrt{3 \times 12} = \sqrt{36} = 6\]
These advanced techniques will help you simplify even the most complex square roots with ease.
Applications of Square Roots in Various Fields
Square roots play a crucial role in various fields, providing fundamental tools for solving complex problems. Here are some key applications:
1. Mathematics and Geometry
Square roots are essential in solving quadratic equations, which are fundamental in algebra. In geometry, square roots are used to determine the lengths of sides in right triangles through the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} \]
where \( c \) is the hypotenuse, and \( a \) and \( b \) are the other two sides of the triangle.
2. Physics
Square roots are used in various physics equations. For example, in mechanics, the formula for the period \( T \) of a pendulum involves the square root:
\[ T = 2\pi \sqrt{\frac{L}{g}} \]
where \( L \) is the length of the pendulum and \( g \) is the acceleration due to gravity.
3. Engineering
Engineers use square roots in numerous calculations, including stress and strain analysis in materials, signal processing, and electrical engineering. For instance, in AC circuit analysis, the root mean square (RMS) value of an alternating current is given by:
\[ I_{\text{RMS}} = \sqrt{\frac{1}{T} \int_0^T [i(t)]^2 \, dt} \]
where \( i(t) \) is the instantaneous current and \( T \) is the period.
4. Statistics
In statistics, the standard deviation, which measures the dispersion of a data set, is derived using the square root of the variance:
\[ \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2} \]
where \( \sigma \) is the standard deviation, \( N \) is the number of observations, \( x_i \) is each individual observation, and \( \mu \) is the mean.
5. Computer Graphics
In computer graphics, square roots are used in algorithms for rendering images, calculating distances, and normalizing vectors. For instance, to calculate the Euclidean distance between two points in a 2D space:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
where \( (x_1, y_1) \) and \( (x_2, y_2) \) are the coordinates of the two points.
6. Finance
In finance, square roots are used to model the volatility of stock prices through the standard deviation. Additionally, the formula for calculating compound interest involves the square root in certain contexts:
\[ FV = PV \left(1 + \frac{r}{n}\right)^{nt} \]
where \( FV \) is the future value, \( PV \) is the present value, \( r \) is the annual interest rate, \( n \) is the number of times interest is compounded per year, and \( t \) is the time in years.
7. Medicine
In medical research, square roots are used in pharmacokinetics to describe the rates at which drugs are absorbed, distributed, metabolized, and excreted. The half-life of a drug, which is the time required for its concentration to reduce to half, is often calculated using square root functions.
These examples highlight the versatility and importance of square roots across different disciplines, illustrating their wide-ranging applications and significance.
Conclusion and Further Resources
Simplifying square roots can be a valuable skill in various mathematical contexts, from solving algebraic equations to practical applications in science and engineering. By understanding the properties and methods for simplifying square roots, you can enhance your problem-solving abilities and gain a deeper appreciation for the elegance of mathematics.
Throughout this guide, we've explored the fundamental concepts and techniques needed to simplify square roots effectively. From basic properties and prime factorization to advanced methods, these tools will help you tackle a wide range of problems with confidence.
For those seeking further resources and practice, consider the following:
- - An online tool that helps you calculate and understand square roots.
- - Provides step-by-step solutions for square root calculations and more.
- - Simplifies square roots to their simplest radical form and offers additional mathematical tools.
- - A comprehensive calculator that explains the process of simplifying square roots.
By utilizing these resources, you can continue to refine your skills and apply square root simplification techniques to a variety of mathematical challenges. Remember, practice is key to mastering these concepts, so take advantage of the tools and examples provided to further your understanding.
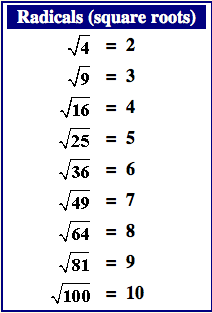
Hướng dẫn cách đơn giản hóa căn bậc hai bằng máy tính đồ thị, phù hợp cho người học toán.
Đơn Giản Hóa Căn Bậc Hai Với Máy Tính Đồ Thị
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai một cách dễ hiểu, phù hợp cho người học toán.
Cách Đơn Giản Hóa Căn Bậc Hai