Topic simplify square root of 44: Understanding how to simplify the square root of 44 can help in various mathematical problems. This guide breaks down the process step-by-step, using prime factorization and the product rule for radicals. Learn how to simplify √44 effectively and explore practical examples and common mistakes to avoid.
Table of Content
- Simplifying the Square Root of 44
- Introduction
- Understanding Square Roots
- Prime Factorization Method
- Step-by-Step Simplification Process
- Applying the Product Rule for Radicals
- Examples of Simplified Square Roots
- Common Mistakes and How to Avoid Them
- Practice Problems
- Advanced Concepts and Related Topics
- FAQs about Simplifying Square Roots
- Conclusion
- YOUTUBE: Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 44. Video này giải thích từng bước cách thực hiện và giúp bạn hiểu rõ hơn về việc đơn giản hóa căn bậc hai.
Simplifying the Square Root of 44
To simplify the square root of 44, we can use the prime factorization method. The number 44 can be factored into prime numbers. Here is a step-by-step explanation:
- Factor 44 into its prime factors:
- 44 = 2 × 22
- 22 = 2 × 11
- Rewrite the square root of 44 using these factors:
\[\sqrt{44} = \sqrt{2^2 \times 11}\]
- Apply the product rule for radicals:
\[\sqrt{44} = \sqrt{2^2} \times \sqrt{11}\]
- Simplify the expression by taking the square root of the perfect square (22):
\[\sqrt{2^2} = 2\]
- Combine the simplified terms:
\[\sqrt{44} = 2\sqrt{11}\]
Thus, the simplified form of the square root of 44 is \(2\sqrt{11}\).
Examples and Practice Problems
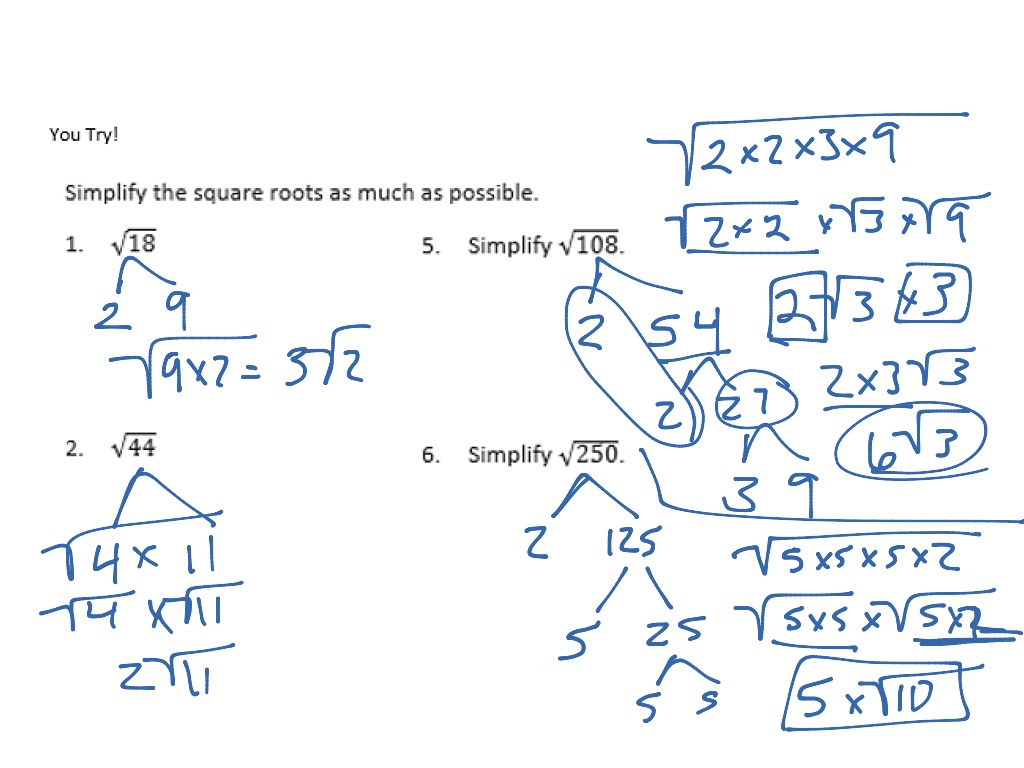
- Simplify \(\sqrt{18}\):
\(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\)
- Simplify \(\sqrt{50}\):
\(\sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2}\)
- Simplify \(\sqrt{72}\):
\(\sqrt{72} = \sqrt{2^3 \times 3^2} = 6\sqrt{2}\)
- Simplify \(\sqrt{88}\):
\(\sqrt{88} = \sqrt{2^3 \times 11} = 2\sqrt{22}\)
| Number | Simplified Form |
|---|---|
| \(\sqrt{44}\) | 2\(\sqrt{11}\) |
| \(\sqrt{18}\) | 3\(\sqrt{2}\) |
| \(\sqrt{50}\) | 5\(\sqrt{2}\) |
| \(\sqrt{72}\) | 6\(\sqrt{2}\) |
| \(\sqrt{88}\) | 2\(\sqrt{22}\) |

READ MORE:
Introduction
Understanding the process of simplifying the square root of 44 can greatly aid in solving various mathematical problems. Simplifying square roots involves breaking down the number inside the radical into its prime factors and then applying the product rule for radicals. This comprehensive guide will take you through the step-by-step process, providing clear explanations and practical examples to ensure you grasp the concept thoroughly.
We start by factoring 44 into its prime components:
- 44 can be expressed as \(2^2 \times 11\).
- This means we can rewrite \(\sqrt{44}\) as \(\sqrt{2^2 \times 11}\).
Using the product rule for radicals, which states \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\), we simplify further:
- \(\sqrt{2^2 \times 11} = \sqrt{2^2} \times \sqrt{11}\).
- Since \(\sqrt{2^2} = 2\), we get \(2 \sqrt{11}\).
Thus, the simplified form of \(\sqrt{44}\) is \(2 \sqrt{11}\). This method not only simplifies the calculation but also makes it easier to work with the number in further mathematical operations.
Understanding Square Roots
Square roots are a fundamental concept in mathematics, representing a number that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because 4 × 4 = 16. In general, for any positive number \( a \), the square root of \( a \) is denoted as \( \sqrt{a} \).
To simplify square roots, especially when dealing with non-perfect squares, we often break them down into their prime factors. This involves expressing the number inside the square root as a product of its factors and then simplifying where possible.
Let's take the example of simplifying \( \sqrt{44} \):
- First, factor 44 into its prime factors: \( 44 = 2^2 \times 11 \).
- Rewrite the square root using these factors: \( \sqrt{44} = \sqrt{2^2 \times 11} \).
- Separate the factors inside the square root: \( \sqrt{2^2} \times \sqrt{11} \).
- Simplify the square root of the perfect square: \( \sqrt{2^2} = 2 \).
Therefore, \( \sqrt{44} = 2\sqrt{11} \).
Understanding this process helps in dealing with more complex square root problems and is a fundamental skill in algebra. By practicing these steps, one can quickly simplify square roots and solve related mathematical problems more efficiently.
Prime Factorization Method
The prime factorization method is a systematic way to simplify the square root of a number by breaking it down into its prime factors. Here’s how to simplify the square root of 44 using this method:
- First, find the prime factors of 44. The prime factors of 44 are 2 and 11, so we can write:
\(44 = 2 \times 2 \times 11\)
- Next, group the prime factors in pairs. In this case, we have one pair of 2s and one 11:
\(44 = (2 \times 2) \times 11\)
- Take one factor from each pair. For the pair of 2s, take one 2:
\(\sqrt{44} = \sqrt{(2^2) \times 11} = 2 \sqrt{11}\)
- Therefore, the simplified form of the square root of 44 is:
\(\sqrt{44} = 2\sqrt{11}\)
This method helps to express the square root in its simplest radical form, making it easier to understand and use in further calculations.
Step-by-Step Simplification Process
To simplify the square root of 44, follow these detailed steps:
-
Find the prime factorization of 44:
- 44 can be factored into 2 and 22.
- 22 can be further factored into 2 and 11.
- Thus, the prime factorization of 44 is \( 2^2 \times 11 \).
-
Express the square root of 44 using its prime factors:
\(\sqrt{44} = \sqrt{2^2 \times 11}\)
-
Apply the property of square roots that states \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):
\(\sqrt{2^2 \times 11} = \sqrt{2^2} \times \sqrt{11}\)
-
Simplify the square root of the perfect square (2 squared):
\(\sqrt{2^2} = 2\)
-
Combine the simplified square root with the remaining factor:
\(2 \times \sqrt{11}\)
-
Thus, the simplified form of the square root of 44 is:
\(\sqrt{44} = 2\sqrt{11}\)
By following these steps, you can easily simplify the square root of 44 to its simplest form, \(2\sqrt{11}\).

Applying the Product Rule for Radicals
The Product Rule for Radicals is a fundamental principle that simplifies the multiplication of radicals. According to this rule, the square root of a product is equal to the product of the square roots of the factors. This means that for any non-negative numbers \(a\) and \(b\), the following equation holds true:
\(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\)
Let's apply this rule to simplify the square root of 44 step-by-step.
- Identify the factors of 44 that include a perfect square. The factors of 44 are 1, 2, 4, 11, 22, and 44. The largest perfect square factor is 4.
- Rewrite 44 as the product of its factors: \(44 = 4 \times 11\).
- Apply the Product Rule: \(\sqrt{44} = \sqrt{4 \times 11} = \sqrt{4} \cdot \sqrt{11}\).
- Simplify the square roots: \(\sqrt{4} = 2\), so the expression becomes \(2 \cdot \sqrt{11}\).
Therefore, the simplified form of \(\sqrt{44}\) is \(2\sqrt{11}\). This method can be used to simplify any square root by breaking down the radicand into its factors, applying the Product Rule, and simplifying the resulting expressions.
Examples of Simplified Square Roots
Simplifying square roots involves breaking down the number under the radical into its prime factors and using the product rule to separate the perfect squares. Here are some examples that demonstrate this process in a detailed, step-by-step manner.
-
Example 1: Simplify \( \sqrt{72} \)
- Factor 72 into prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Group the pairs: \( 72 = (2 \times 2 \times 3 \times 3) \times 2 = 36 \times 2 \).
- Separate the square root: \( \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} \).
- Simplify: \( \sqrt{36} = 6 \), so \( \sqrt{72} = 6\sqrt{2} \).
-
Example 2: Simplify \( \sqrt{288} \)
- Factor 288 into prime factors: \( 288 = 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 2 \).
- Group the pairs: \( 288 = (2 \times 2 \times 2 \times 2 \times 3 \times 3) \times 2 = 144 \times 2 \).
- Separate the square root: \( \sqrt{288} = \sqrt{144 \times 2} = \sqrt{144} \times \sqrt{2} \).
- Simplify: \( \sqrt{144} = 12 \), so \( \sqrt{288} = 12\sqrt{2} \).
-
Example 3: Simplify \( \sqrt{108} \)
- Factor 108 into prime factors: \( 108 = 2 \times 2 \times 3 \times 3 \times 3 \).
- Group the pairs: \( 108 = (2 \times 3 \times 3) \times 3 = 9 \times 12 \).
- Separate the square root: \( \sqrt{108} = \sqrt{36 \times 3} = \sqrt{36} \times \sqrt{3} \).
- Simplify: \( \sqrt{36} = 6 \), so \( \sqrt{108} = 6\sqrt{3} \).
These examples illustrate the process of simplifying square roots by breaking down the number into prime factors and using the product rule for radicals to simplify the expression. By practicing these steps, you can become proficient in simplifying any square root.
Common Mistakes and How to Avoid Them
Simplifying square roots can be challenging, and many learners often make similar mistakes. Here are some common errors and tips on how to avoid them:
-
Forgetting to Check for Perfect Squares
One of the most common mistakes is not checking for perfect squares within the number under the square root. Always factorize the number completely to see if there are any perfect square factors.
Example: Instead of simplifying , check if 44 has any perfect square factors. 44 can be written as 4 × 11, and since 4 is a perfect square, we can simplify .
-
Incorrectly Applying the Product Rule
The product rule states that . Misapplying this rule can lead to errors.
Example: To simplify , recognize that 12 is 4 × 3, so .
-
Leaving Square Roots in the Denominator
Square roots should be rationalized in the denominator to simplify the expression. Multiply the numerator and denominator by the square root in the denominator.
Example: To simplify , multiply by to get .
-
Overlooking Simplification of Radicals with Variables
When dealing with variables, remember to simplify the numerical part and the variable part separately, and always look for pairs of variables.
Example: For , write it as .
-
Not Practicing Enough
Practice is crucial for mastering square roots. Work through various problems to become comfortable with different types of simplifications.
Engage in regular practice and seek help from resources like online tutorials or math tutors to strengthen your understanding.
Practice Problems
Here are some practice problems to help you master simplifying square roots, especially focusing on the square root of 44. Each problem is followed by a step-by-step solution to guide you.
-
Simplify
Solution:
- Rewrite 44 as 4 × 11:
- Use the product rule:
- Simplify the perfect square:
- Combine the results:
-
Simplify
Solution:
- Rewrite 72 as 36 × 2:
- Use the product rule:
- Simplify the perfect square:
- Combine the results:
-
Simplify
Solution:
- Rewrite 50 as 25 × 2:
- Use the product rule:
- Simplify the perfect square:
- Combine the results:
-
Simplify
Solution:
- Rewrite 98 as 49 × 2:
- Use the product rule:
- Simplify the perfect square:
- Combine the results:
These practice problems will help reinforce your understanding of simplifying square roots. Make sure to follow each step carefully and practice regularly to improve your skills.
Advanced Concepts and Related Topics
In this section, we will explore advanced concepts related to simplifying square roots, particularly focusing on the square root of 44, and other related topics in mathematics.
1. Rationalizing the Denominator
Rationalizing the denominator involves rewriting a fraction so that the denominator no longer contains a radical. For example, to rationalize \( \frac{1}{\sqrt{44}} \), multiply the numerator and the denominator by \( \sqrt{44} \):
\[
\frac{1}{\sqrt{44}} \times \frac{\sqrt{44}}{\sqrt{44}} = \frac{\sqrt{44}}{44} = \frac{2\sqrt{11}}{44} = \frac{\sqrt{11}}{22}
\]
2. Operations with Radicals
Understanding how to perform operations with radicals is crucial. Here are a few examples:
- Adding and Subtracting Radicals: Only like radicals can be added or subtracted. For example, \( 2\sqrt{11} + 3\sqrt{11} = 5\sqrt{11} \).
- Multiplying Radicals: Multiply the coefficients and the radicands separately. For example, \( \sqrt{44} \times \sqrt{11} = \sqrt{44 \times 11} = \sqrt{484} = 22 \).
- Dividing Radicals: Divide the coefficients and the radicands separately. For example, \( \frac{\sqrt{44}}{\sqrt{11}} = \sqrt{\frac{44}{11}} = \sqrt{4} = 2 \).
3. Simplifying Higher-Order Roots
While we often deal with square roots, higher-order roots, such as cube roots, also follow similar principles. For instance, the cube root of a product can be broken down:
\[
\sqrt[3]{a \times b} = \sqrt[3]{a} \times \sqrt[3]{b}
\]
4. Complex Numbers
Sometimes, simplifying square roots involves complex numbers, especially when dealing with negative radicands. The imaginary unit \( i \) is defined as \( i = \sqrt{-1} \). For example:
\[
\sqrt{-44} = \sqrt{-1 \times 44} = \sqrt{-1} \times \sqrt{44} = i \times 2\sqrt{11} = 2i\sqrt{11}
\]
5. Applications in Geometry
Square roots are often used in geometry, particularly in calculating distances and areas. The distance formula, derived from the Pythagorean theorem, involves square roots:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
Similarly, the area of a right triangle can be found using the lengths of the legs \( a \) and \( b \):
\[
\text{Area} = \frac{1}{2}ab
\]
6. Related Mathematical Topics
- Exponents and Radicals: The relationship between exponents and radicals is fundamental. For example, \( \sqrt{x} = x^{1/2} \).
- Logarithms: Understanding logarithms can provide deeper insights into the properties of exponents and radicals.
- Polynomials: Simplifying polynomials often involves factoring and using the properties of radicals.
By mastering these advanced concepts and related topics, you'll gain a deeper understanding of how to work with square roots and other mathematical operations.
FAQs about Simplifying Square Roots
Here are some frequently asked questions about simplifying square roots, along with detailed answers to help you understand the concepts better.
1. What is the simplest form of the square root of 44?
The simplest form of the square root of 44 is \(2\sqrt{11}\). This is obtained by factoring 44 into \(4 \times 11\) and then taking the square root of 4, which is 2.
\[
\sqrt{44} = \sqrt{4 \times 11} = \sqrt{4} \times \sqrt{11} = 2\sqrt{11}
\]
2. How do you simplify square roots in general?
To simplify a square root:
- Factor the number into its prime factors.
- Identify and pair the factors that are perfect squares.
- Take the square root of the perfect squares and multiply the results outside the radical sign.
For example, to simplify \(\sqrt{72}\):
\[
\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}
\]
3. Can square roots always be simplified?
No, not all square roots can be simplified. When the number inside the square root does not have any perfect square factors (other than 1), the square root cannot be simplified further. Such square roots are called "surd". For example, \(\sqrt{3}\) is a surd because it cannot be simplified further.
4. What are common mistakes to avoid when simplifying square roots?
- Forgetting to factor the number completely. Ensure you find all prime factors to identify perfect squares correctly.
- Not pairing the factors correctly. Remember to pair the factors under the square root before simplifying.
- Incorrectly simplifying non-perfect square factors. Only perfect square factors should be simplified outside the radical sign.
5. How do you handle square roots in the denominator?
When you have a square root in the denominator, you should rationalize the denominator by multiplying the numerator and the denominator by the same square root to eliminate the radical from the denominator.
For example, to rationalize \(\frac{1}{\sqrt{44}}\):
\[
\frac{1}{\sqrt{44}} \times \frac{\sqrt{44}}{\sqrt{44}} = \frac{\sqrt{44}}{44} = \frac{2\sqrt{11}}{44} = \frac{\sqrt{11}}{22}
\]
6. Are there any tools to help simplify square roots?
Yes, there are several online calculators and tools that can help you simplify square roots. These tools can factor the number for you and provide the simplified form. Some popular ones include Mathway and Symbolab.
By understanding these common questions and their answers, you can improve your skills in simplifying square roots and avoid common mistakes.
Conclusion
Simplifying the square root of 44 demonstrates the importance of understanding prime factorization and the product rule for radicals. By breaking down the number into its prime factors, we can effectively simplify square roots and make complex mathematical problems more manageable.
To summarize, the key steps in simplifying the square root of 44 are:
- Identify the largest perfect square factor of 44, which is 4.
- Express 44 as the product of 4 and 11.
- Apply the product rule for radicals: .
- Simplify: , so .
By following these steps, we find that
Understanding these principles not only helps with simplifying square roots but also provides a foundation for more advanced mathematical concepts. With practice and application of these techniques, you can confidently approach and solve a variety of problems involving square roots.
Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 44. Video này giải thích từng bước cách thực hiện và giúp bạn hiểu rõ hơn về việc đơn giản hóa căn bậc hai.
Làm Thế Nào Để Đơn Giản Hóa Căn Bậc Hai Của 44: Sqrt(44)
READ MORE:
Hướng dẫn cách đơn giản hóa căn bậc hai của 44 một cách dễ hiểu và chi tiết. Video này sẽ giúp bạn nắm vững các bước đơn giản hóa căn bậc hai của số 44.
Làm Thế Nào Để Đơn Giản Hóa Căn Bậc Hai Của 44











