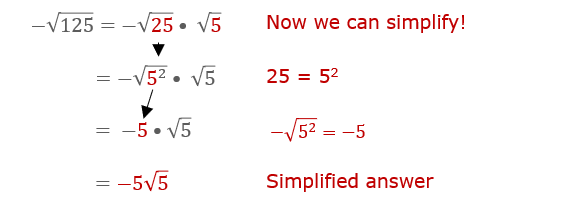Topic simplify square roots: Simplifying square roots doesn't have to be daunting. In this comprehensive guide, we'll break down easy and effective techniques to help you master the art of simplifying square roots. Whether you're dealing with perfect squares, non-perfect squares, or variables, you'll find clear steps and examples to make the process straightforward and manageable.
Table of Content
- Simplifying Square Roots
- Introduction to Square Roots
- What Are Square Roots?
- Importance of Simplifying Square Roots
- Basic Principles of Square Roots
- Step-by-Step Guide to Simplifying Square Roots
- Simplifying Square Roots of Perfect Squares
- Finding the Largest Perfect Square Factor
- Dealing with Square Roots and Fractions
- Common Patterns in Square Root Simplification
- Square Root Simplification Examples
- Handling Complex Square Root Expressions
- Square Roots in Radical Form
- Using Prime Factorization for Simplification
- Practical Applications of Simplified Square Roots
- Common Mistakes to Avoid
- Advanced Techniques for Simplifying Square Roots
- Practice Problems for Simplifying Square Roots
- Conclusion and Tips for Mastery
- YOUTUBE: Xem video này để học cách rút gọn căn bậc hai một cách hiệu quả. Có phù hợp với bài viết về đơn giản hóa căn bậc hai không?
Simplifying Square Roots
Simplifying square roots is a fundamental skill in algebra that involves reducing a square root to its simplest form. The process typically includes factoring the number under the square root (the radicand) to identify perfect squares.
Basic Steps to Simplify Square Roots
- Identify the largest perfect square factor of the radicand.
- Rewrite the radicand as a product of the perfect square and another number.
- Take the square root of the perfect square outside the square root sign.
- Multiply the result by the square root of the remaining factor.
For example, to simplify \( \sqrt{72} \):
- Factor 72 to find its largest perfect square factor: \( 72 = 36 \times 2 \).
- Rewrite the square root as \( \sqrt{36 \times 2} \).
- Separate the product into two square roots: \( \sqrt{36} \times \sqrt{2} \).
- Simplify \( \sqrt{36} \) to 6, resulting in \( 6\sqrt{2} \).
Simplifying Square Roots of Non-Perfect Squares
When the radicand is not a perfect square, we look for the largest perfect square factor:
- For \( \sqrt{50} \), factor as \( 50 = 25 \times 2 \).
- Rewrite \( \sqrt{50} \) as \( \sqrt{25 \times 2} \).
- Simplify to \( \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \).
Simplifying Square Roots with Variables
When variables are involved, apply the same principles while treating the variables as factors:
- For \( \sqrt{50x^4} \), factor into \( \sqrt{25 \times 2 \times x^4} \).
- Simplify to \( \sqrt{25} \times \sqrt{2} \times \sqrt{x^4} = 5 \times \sqrt{2} \times x^2 \).
- The result is \( 5x^2\sqrt{2} \).
Common Simplification Patterns
- \( \sqrt{a^2b} = a\sqrt{b} \)
- \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
Example Problems
| Expression | Simplified Form |
|---|---|
| \( \sqrt{32} \) | \( 4\sqrt{2} \) |
| \( \sqrt{18} \) | \( 3\sqrt{2} \) |
| \( \sqrt{48x^2} \) | \( 4x\sqrt{3} \) |
| \( \sqrt{75y^6} \) | \( 5y^3\sqrt{3} \) |
Practice Problems
Try simplifying these square roots:
- \( \sqrt{98} \)
- \( \sqrt{200} \)
- \( \sqrt{72x^3} \)
- \( \sqrt{45y^2} \)
Use the steps and patterns provided above to simplify these expressions. Practice will help reinforce these techniques and make simplifying square roots easier over time.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 x 3 = 9. Square roots are fundamental in various areas of mathematics and are often represented using the radical symbol (√).
Understanding square roots involves recognizing both perfect squares and non-perfect squares. A perfect square is a number that has an integer as its square root, such as 1, 4, 9, 16, and so on. For non-perfect squares, the square root is an irrational number, which cannot be expressed as a simple fraction and has an infinite, non-repeating decimal expansion.
Below are some key properties and examples to help grasp the concept of square roots:
- Property 1:
- Property 2:
- Property 3:
Here are a few examples of simplifying square roots:
| Expression | Simplified Form |
|---|---|
Understanding and simplifying square roots is a crucial skill that simplifies calculations and helps in solving various mathematical problems. By mastering the basic principles and properties of square roots, you can efficiently handle more complex mathematical tasks involving radicals.
What Are Square Roots?
A square root of a number is a value that, when multiplied by itself, gives the original number. The symbol for the square root is \(\sqrt{}\), called the radical sign.
For example:
- The square root of 9 is 3 because \(3 \times 3 = 9\).
- The square root of 16 is 4 because \(4 \times 4 = 16\).
Mathematically, if \(x\) is the square root of \(y\), then \(x^2 = y\). This means that if we take the square of the square root of a number, we get the original number back.
Positive and Negative Square Roots
Every positive number has two square roots: one positive and one negative. For example:
- The square roots of 25 are 5 and -5 because \(5 \times 5 = 25\) and \((-5) \times (-5) = 25\).
By convention, the symbol \(\sqrt{}\) refers to the principal (positive) square root. So, \(\sqrt{25} = 5\).
Square Roots of Perfect Squares
A perfect square is a number that is the square of an integer. Here are some examples:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Square Roots of Non-Perfect Squares
For numbers that are not perfect squares, their square roots are irrational numbers. This means their decimal form is non-terminating and non-repeating. For example:
- \(\sqrt{2} \approx 1.414\)
- \(\sqrt{3} \approx 1.732\)
Using Square Roots in Equations
Square roots are often used in equations. For instance, to solve \(x^2 = 36\), we take the square root of both sides to get \(x = \pm 6\).
Importance of Simplifying Square Roots
Simplifying square roots is a crucial mathematical skill with wide-ranging applications. Here are some reasons why it is important:
-
Ease of Calculation:
Simplified square roots make complex calculations more manageable. By reducing a square root to its simplest form, you can more easily perform arithmetic operations and solve equations. For example, simplifying \( \sqrt{72} \) to \( 6\sqrt{2} \) makes subsequent calculations straightforward.
-
Mathematical Clarity:
Simplified expressions are often easier to understand and work with. This clarity is particularly important when dealing with algebraic expressions, where simplified square roots can help in identifying patterns and relationships.
-
Practical Applications:
In real-world scenarios, simplified square roots are used in various fields such as engineering, physics, and finance. For instance, in construction, the length of diagonals or the hypotenuse in right-angled triangles can be simplified for more precise measurements.
-
Advanced Mathematics:
Understanding and simplifying square roots lays the groundwork for more advanced topics in mathematics, such as calculus and higher-level algebra. Mastering this skill can help in solving more complex problems efficiently.
-
Error Reduction:
Working with simplified square roots can reduce errors in calculations. Simplified forms are less prone to arithmetic mistakes, ensuring more accurate results in both academic and professional settings.
In summary, the importance of simplifying square roots cannot be overstated. It enhances computational efficiency, provides mathematical clarity, and has numerous practical applications in everyday life.
Basic Principles of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5, because 5 * 5 = 25. In mathematical notation, this is written as √25 = 5.
Here are the basic principles to understand square roots:
- Positive and Negative Roots: Every positive number has two square roots, one positive and one negative. For example, both 3 and -3 are square roots of 9 because 3 * 3 = 9 and (-3) * (-3) = 9. However, in most cases, the term "square root" generally refers to the positive root.
- Product Property: The square root of a product is equal to the product of the square roots of each factor. In mathematical terms, this is written as:
- √(a * b) = √a * √b
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator:
- √(a / b) = √a / √b
- Simplifying Square Roots: To simplify a square root, factor the number into its prime factors and then apply the product property. If any factors are perfect squares, take their square roots out of the radical:
- For example, to simplify √72:
- Factor 72 into 36 * 2.
- Since 36 is a perfect square, √72 = √(36 * 2) = √36 * √2 = 6√2.
- For example, to simplify √72:
- Perfect Squares: A perfect square is an integer that is the square of another integer. For example, 1, 4, 9, 16, 25, etc., are perfect squares. The square root of a perfect square is always an integer.
- For example, √16 = 4 and √81 = 9.
Understanding these basic principles is essential for simplifying square roots and solving more complex mathematical problems involving radicals.
Step-by-Step Guide to Simplifying Square Roots
Simplifying square roots involves breaking down the number inside the radical to its simplest form. Follow these steps for a structured approach:
-
Factor the Number:
Break down the number inside the square root into its prime factors. This helps in identifying pairs of factors.
- Example: Simplify \( \sqrt{72} \)
- Prime factorization: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
-
Identify and Separate Perfect Squares:
Group the prime factors into pairs and separate them under the square root.
- Using \( \sqrt{72} \) as an example:
- Pairs: \( 72 = (2 \times 2) \times (3 \times 3) \times 2 \)
- Separate: \( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} \)
-
Simplify:
Take one number from each pair out of the square root and multiply them. Multiply the remaining factors inside the radical.
- Example: \( \sqrt{72} = \sqrt{4 \times 9 \times 2} = \sqrt{4} \times \sqrt{9} \times \sqrt{2} \)
- Simplify further: \( 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \)
Additional Examples
Here are more examples to illustrate the process:
- \( \sqrt{45} \)
- Prime factorization: \( 45 = 3 \times 3 \times 5 \)
- Simplify: \( \sqrt{45} = \sqrt{(3 \times 3) \times 5} = 3\sqrt{5} \)
- \( \sqrt{50} \)
- Prime factorization: \( 50 = 2 \times 5 \times 5 \)
- Simplify: \( \sqrt{50} = \sqrt{2 \times (5 \times 5)} = 5\sqrt{2} \)
Simplifying Square Roots with Fractions
The same principles apply when simplifying square roots involving fractions:
- Combine the square roots of the numerator and denominator.
- Example: \( \sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}} = \frac{5}{3} \)
Using Prime Factorization
An alternative method to simplify square roots is through prime factorization:
- Factor the number into primes.
- Identify pairs of prime factors.
- Take one number out of each pair and multiply.
- Example: \( \sqrt{18} \)
- Prime factorization: \( 18 = 2 \times 3 \times 3 \)
- Simplify: \( \sqrt{18} = \sqrt{2 \times (3 \times 3)} = 3\sqrt{2} \)
Simplifying Square Roots of Perfect Squares
Simplifying square roots of perfect squares is a fundamental concept in mathematics. Perfect squares are numbers that are the square of an integer. Here’s how you can simplify the square roots of perfect squares step by step:
-
Identify the Perfect Square:
First, recognize that a perfect square is a number that can be expressed as \( n^2 \), where \( n \) is an integer. For example, 4, 9, 16, 25, and 36 are perfect squares because they are \( 2^2 \), \( 3^2 \), \( 4^2 \), \( 5^2 \), and \( 6^2 \) respectively.
-
Apply the Square Root:
When you take the square root of a perfect square, you get the integer that was squared to produce that number. For example:
- \(\sqrt{4} = 2\) because \( 2^2 = 4 \)
- \(\sqrt{9} = 3\) because \( 3^2 = 9 \)
- \(\sqrt{16} = 4\) because \( 4^2 = 16 \)
- \(\sqrt{25} = 5\) because \( 5^2 = 25 \)
- \(\sqrt{36} = 6\) because \( 6^2 = 36 \)
-
Simplification:
The square root of a perfect square simplifies directly to an integer. This makes calculations involving perfect squares straightforward and simple. For example:
- \(\sqrt{49} = 7\)
- \(\sqrt{64} = 8\)
- \(\sqrt{81} = 9\)
- \(\sqrt{100} = 10\)
To further illustrate, consider the following example:
Example: Simplify \(\sqrt{144}\)
Since 144 is a perfect square (as \( 12^2 = 144 \)), the simplification is:
\(\sqrt{144} = 12\)
This method of simplification can be applied to any perfect square. It is especially useful in solving algebraic equations and in simplifying expressions that involve square roots.
Finding the Largest Perfect Square Factor
To simplify square roots effectively, it is essential to find the largest perfect square factor of the given number. Here is a step-by-step guide to help you identify and utilize the largest perfect square factor:
- Understand Perfect Squares:
A perfect square is a number that can be expressed as the product of an integer with itself. For example, \(1, 4, 9, 16, 25\), and so on are perfect squares.
- List the Perfect Squares:
Before you start finding the perfect square factors, it is helpful to have a list of perfect squares handy. Here are the first few:
- \(1 = 1 \times 1\)
- \(4 = 2 \times 2\)
- \(9 = 3 \times 3\)
- \(16 = 4 \times 4\)
- \(25 = 5 \times 5\)
- \(36 = 6 \times 6\)
- \(49 = 7 \times 7\)
- \(64 = 8 \times 8\)
- \(81 = 9 \times 9\)
- \(100 = 10 \times 10\)
- Prime Factorization:
To find the largest perfect square factor, first perform the prime factorization of the given number. For example, let's take \(48\):
\(48 = 2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3\)
- Identify Pairs of Factors:
Group the prime factors into pairs. Each pair of the same number represents a perfect square. In our example:
\(48 = 2^4 \times 3 = (2 \times 2) \times (2 \times 2) \times 3 = 4 \times 4 \times 3\)
- Determine the Largest Perfect Square Factor:
The largest perfect square factor is obtained by multiplying the largest set of pairs. For \(48\), the largest perfect square factor is:
\(2^4 = (2 \times 2) \times (2 \times 2) = 16\)
- Verification:
Verify by dividing the original number by the largest perfect square factor:
\( \frac{48}{16} = 3\)
Thus, \(48\) can be expressed as \(16 \times 3\).
- Simplify the Square Root:
Finally, simplify the square root using the largest perfect square factor:
\(\sqrt{48} = \sqrt{16 \times 3} = \sqrt{16} \times \sqrt{3} = 4\sqrt{3}\)
Using this method, you can efficiently find and utilize the largest perfect square factor to simplify any square root expression.
Dealing with Square Roots and Fractions
Simplifying square roots in fractions involves a few key steps. These steps help in making the fraction easier to work with by eliminating the square roots from the denominator. Here’s a detailed guide:
-
Simplify the Square Roots:
Start by simplifying any square roots present in the fraction. This involves breaking down the square root into its prime factors and simplifying where possible.
- Example:
\( \frac{\sqrt{50}}{2} \) becomes \( \frac{\sqrt{25 \cdot 2}}{2} = \frac{5\sqrt{2}}{2} \)
- Example:
-
Rationalize the Denominator:
If there is a square root in the denominator, multiply the numerator and the denominator by the conjugate or the square root present in the denominator to eliminate it.
- Example:
\( \frac{5}{\sqrt{3}} \)
Multiply by \( \frac{\sqrt{3}}{\sqrt{3}} \) to get \( \frac{5\sqrt{3}}{3} \)
- Example:
-
Combine Like Terms:
Once the denominators are rationalized, simplify the fraction by combining any like terms and reducing it to its simplest form if possible.
- Example:
\( \frac{3\sqrt{5}}{\sqrt{10}} \)
Simplify to \( \frac{3\sqrt{5}}{\sqrt{2 \cdot 5}} = \frac{3\sqrt{5}}{\sqrt{2}\sqrt{5}} = \frac{3}{\sqrt{2}} \)
Rationalize to get \( \frac{3}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{3\sqrt{2}}{2} \)
- Example:
Examples
-
Simplify \( \frac{2}{\sqrt{12}} \):
Simplify the square root: \( \sqrt{12} = 2\sqrt{3} \)
The fraction becomes \( \frac{2}{2\sqrt{3}} = \frac{1}{\sqrt{3}} \)
Rationalize the denominator: \( \frac{1}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3} \) -
Simplify \( \frac{\sqrt{18}}{3} \):
Simplify the square root: \( \sqrt{18} = 3\sqrt{2} \)
The fraction becomes \( \frac{3\sqrt{2}}{3} = \sqrt{2} \)
By following these steps, you can simplify fractions involving square roots effectively, making them easier to handle in mathematical calculations.

Common Patterns in Square Root Simplification
Simplifying square roots often involves recognizing and applying common patterns. These patterns can help you quickly and accurately simplify radical expressions. Here are some of the most common patterns to look for:
-
Perfect Square Factors:
Identify the largest perfect square factor of the number under the square root (radicand). For example, for , the largest perfect square factor is 36.
Example:
-
Prime Factorization:
Break down the radicand into its prime factors and look for pairs of prime factors.
Example:
-
Product Rule:
Use the product rule for square roots, which states that
Example:
-
Quotient Rule:
Apply the quotient rule for square roots, which states that
Example:
-
Recognizing Patterns with Variables:
When simplifying square roots that include variables, look for patterns such as even powers of variables.
Example:
These common patterns help streamline the process of simplifying square roots, making it easier and more efficient. Practice recognizing these patterns to enhance your simplification skills.
Square Root Simplification Examples
Below are detailed examples illustrating how to simplify square roots step-by-step.
Example 1: Simplify \( \sqrt{12} \)
- Factorize 12 into its prime factors: \( 12 = 4 \times 3 \).
- Write the square root as the product of square roots: \( \sqrt{12} = \sqrt{4 \times 3} \).
- Separate the square roots: \( \sqrt{4} \times \sqrt{3} \).
- Simplify the square root of 4: \( 2 \times \sqrt{3} \).
- Final simplified form: \( \sqrt{12} = 2\sqrt{3} \).
Example 2: Simplify \( \sqrt{45} \)
- Factorize 45 into its prime factors: \( 45 = 9 \times 5 \).
- Write the square root as the product of square roots: \( \sqrt{45} = \sqrt{9 \times 5} \).
- Separate the square roots: \( \sqrt{9} \times \sqrt{5} \).
- Simplify the square root of 9: \( 3 \times \sqrt{5} \).
- Final simplified form: \( \sqrt{45} = 3\sqrt{5} \).
Example 3: Simplify \( \sqrt{72} \)
- Factorize 72 into its prime factors: \( 72 = 36 \times 2 \).
- Write the square root as the product of square roots: \( \sqrt{72} = \sqrt{36 \times 2} \).
- Separate the square roots: \( \sqrt{36} \times \sqrt{2} \).
- Simplify the square root of 36: \( 6 \times \sqrt{2} \).
- Final simplified form: \( \sqrt{72} = 6\sqrt{2} \).
Example 4: Simplify \( \sqrt{50} \)
- Factorize 50 into its prime factors: \( 50 = 25 \times 2 \).
- Write the square root as the product of square roots: \( \sqrt{50} = \sqrt{25 \times 2} \).
- Separate the square roots: \( \sqrt{25} \times \sqrt{2} \).
- Simplify the square root of 25: \( 5 \times \sqrt{2} \).
- Final simplified form: \( \sqrt{50} = 5\sqrt{2} \).
Example 5: Simplify \( \sqrt{18} \)
- Factorize 18 into its prime factors: \( 18 = 9 \times 2 \).
- Write the square root as the product of square roots: \( \sqrt{18} = \sqrt{9 \times 2} \).
- Separate the square roots: \( \sqrt{9} \times \sqrt{2} \).
- Simplify the square root of 9: \( 3 \times \sqrt{2} \).
- Final simplified form: \( \sqrt{18} = 3\sqrt{2} \).
Example 6: Simplify \( \sqrt{32} \)
- Factorize 32 into its prime factors: \( 32 = 16 \times 2 \).
- Write the square root as the product of square roots: \( \sqrt{32} = \sqrt{16 \times 2} \).
- Separate the square roots: \( \sqrt{16} \times \sqrt{2} \).
- Simplify the square root of 16: \( 4 \times \sqrt{2} \).
- Final simplified form: \( \sqrt{32} = 4\sqrt{2} \).
Example 7: Simplify \( \sqrt{\frac{72z^{12}}{2z^{10}}} \)
- Simplify the fraction inside the square root: \( \frac{72z^{12}}{2z^{10}} = 36z^2 \).
- Write the square root of the simplified expression: \( \sqrt{36z^2} \).
- Simplify the square root: \( 6z \).
- Final simplified form: \( \sqrt{\frac{72z^{12}}{2z^{10}}} = 6z \).
Example 8: Simplify \( \sqrt{\frac{27m^3}{196}} \)
- Simplify the fraction inside the square root: \( \frac{27m^3}{196} \) cannot be simplified further.
- Use the quotient property to separate the square root: \( \frac{\sqrt{27m^3}}{\sqrt{196}} \).
- Simplify the numerator and the denominator: \( \frac{3m\sqrt{3m}}{14} \).
- Final simplified form: \( \sqrt{\frac{27m^3}{196}} = \frac{3m\sqrt{3m}}{14} \).
Handling Complex Square Root Expressions
When dealing with complex square root expressions, the following steps can help simplify them:
- Identify the parts of the expression that can be simplified separately.
- Use properties of square roots, such as the product property: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\), and the quotient property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- Break down the expression into manageable parts.
- Combine and simplify the parts.
Here are some examples to illustrate the process:
Example 1: Simplifying \(\sqrt{50}\)
- First, factorize 50 into prime factors: \(50 = 2 \times 5^2\).
- Use the product property of square roots: \(\sqrt{50} = \sqrt{2 \times 25} = \sqrt{2} \times \sqrt{25}\).
- Simplify: \(\sqrt{25} = 5\), so \(\sqrt{50} = 5\sqrt{2}\).
Example 2: Simplifying \(\sqrt{\frac{45}{5}}\)
- First, simplify the fraction: \(\frac{45}{5} = 9\).
- Apply the square root: \(\sqrt{9} = 3\).
Example 3: Simplifying \(\sqrt{a^4 \cdot b^2}\)
- Separate the variables: \(\sqrt{a^4 \cdot b^2} = \sqrt{a^4} \cdot \sqrt{b^2}\).
- Simplify each part: \(\sqrt{a^4} = a^2\) and \(\sqrt{b^2} = b\).
- Combine the simplified parts: \(a^2 \cdot b\).
Example 4: Simplifying Complex Expressions with Variables
- Consider the expression: \(\sqrt{50x^2y}\).
- Factorize inside the square root: \(50x^2y = 2 \cdot 5^2 \cdot x^2 \cdot y\).
- Use the product property: \(\sqrt{50x^2y} = \sqrt{2 \cdot 25 \cdot x^2 \cdot y} = \sqrt{2} \cdot \sqrt{25} \cdot \sqrt{x^2} \cdot \sqrt{y}\).
- Simplify: \(\sqrt{25} = 5\) and \(\sqrt{x^2} = x\), so \(\sqrt{50x^2y} = 5x\sqrt{2y}\).
These examples show the importance of breaking down complex square root expressions into simpler parts and using fundamental properties of square roots to simplify them step-by-step.
Square Roots in Radical Form
The square root symbol (√) is known as a radical, and the number under the radical sign is called the radicand. Simplifying square roots often involves expressing the radicand in a more manageable form.
To simplify square roots, follow these steps:
-
Identify the largest perfect square factor of the radicand.
- For example, in √72, the largest perfect square factor is 36 because 36 × 2 = 72.
-
Rewrite the radicand as a product of the perfect square and another factor.
- √72 = √(36 × 2)
-
Use the property of square roots that √(a × b) = √a × √b to separate the factors.
- √(36 × 2) = √36 × √2
-
Simplify the square root of the perfect square.
- √36 = 6
-
Combine the simplified square root with the remaining factor.
- √72 = 6√2
Here are more examples to illustrate the process:
| Radicand | Simplified Form |
|---|---|
| √50 | √(25 × 2) = 5√2 |
| √98 | √(49 × 2) = 7√2 |
| √200 | √(100 × 2) = 10√2 |
Simplifying square roots makes it easier to work with radical expressions in algebra and calculus, allowing for cleaner and more manageable solutions.

Using Prime Factorization for Simplification
The prime factorization method is a systematic way to simplify square roots by breaking down the number into its prime factors. Here’s a step-by-step guide:
-
Factorize the Number:
Begin by dividing the number by the smallest prime number (usually 2) that can exactly divide it without leaving a remainder. Continue this process with the quotient until you reach a prime number. This will give you the prime factors of the number.
Example: To factorize 72:
- 72 ÷ 2 = 36
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
The prime factors of 72 are: \(2^3 \times 3^2\)
-
Organize the Prime Factors into Pairs:
Arrange the prime factors in a visible format (like a list) and pair identical factors. If a factor does not have a pair, it remains single.
Example: From the prime factors \(2^3 \times 3^2\):
- Pairs are: (2, 2), (2), (3, 3)
- Unpaired factor: 2
-
Multiply One Element from Each Pair:
For each pair of identical primes, select one prime from the pair and multiply them. If a prime remains unpaired, it stays under the square root.
Example: From the pairs (2, 2) and (3, 3):
- Multiply one element from each pair: 2 × 3 = 6
-
Calculate the Square Root:
Multiply the results of the previous step together, and multiply this product by the square root of any leftover unpaired primes to find the square root of the original number.
Example: The paired result is 6, and the unpaired prime is 2:
- The square root of 72 is \(6 \sqrt{2}\)
Examples
Example 1: Simplify the square root of 144.
- Prime factorize 144: \(144 = 2^4 \times 3^2\)
- Pair the factors: (2, 2), (2, 2), (3, 3)
- Multiply one from each pair: \(2 \times 2 \times 3 = 12\)
- The square root of 144 is \(12\).
Example 2: Simplify the square root of 200.
- Prime factorize 200: \(200 = 2^3 \times 5^2\)
- Pair the factors: (2, 2), (5, 5)
- Multiply one from each pair: \(2 \times 5 = 10\)
- The square root of 200 is \(10 \sqrt{2}\).
Using prime factorization is a reliable method to simplify square roots, making it easier to handle larger numbers and ensure accurate results.
Practical Applications of Simplified Square Roots
Simplified square roots are not just a theoretical concept but have numerous practical applications across various fields. Here are some examples:
- Finance: Square roots are used in calculating stock market volatility, which helps investors assess the risk of investments by taking the square root of the return variance.
- Architecture: Engineers use square roots to determine the natural frequency of structures such as bridges and buildings to predict their response to different loads, such as wind or traffic.
- Science: In physics, square roots are used to calculate the velocity of moving objects, the amount of radiation absorbed by materials, and the intensity of sound waves.
- Statistics: Square roots are used to find the standard deviation, a measure of data dispersion. The standard deviation is the square root of the variance.
- Geometry: Calculating the area and perimeter of shapes often involves square roots. For example, the Pythagorean theorem uses square roots to find the lengths of sides in right triangles.
- Computer Science: In programming, square roots are used in encryption algorithms, image processing, and game physics to ensure data security and graphical accuracy.
- Cryptography: Square roots are essential in generating digital signatures and secure communication channels by using properties of prime numbers and modular arithmetic.
- Navigation: Pilots and navigators use square roots to calculate distances between points on a map or globe, crucial for plotting accurate flight paths.
- Electrical Engineering: Square roots help in calculating power, voltage, and current in circuits, as well as in designing filters and signal-processing devices.
- Photography: The f-number in camera lenses, which controls the light entering the camera, is proportional to the square root of the aperture area, affecting exposure and depth of field.
- Computer Graphics: Square roots are used to compute distances and lengths in 2D and 3D graphics, essential for rendering realistic images and animations.
Understanding and applying square roots in these contexts enhances problem-solving abilities and leads to innovations and advancements in technology, finance, science, and engineering.
Common Mistakes to Avoid
When simplifying square roots, it is important to be mindful of common pitfalls that can lead to errors. Here are some frequent mistakes and tips to avoid them:
- Not Checking for Perfect Squares: Always check if the number inside the square root is a perfect square. Simplify it first to avoid unnecessary complications.
- Incorrect Factorization: Ensure you factorize the number inside the square root correctly. Mistakes in prime factorization can lead to incorrect simplification.
- Forgetting to Simplify Completely: After initial simplification, recheck to see if further simplification is possible. This ensures the simplest form.
- Misapplying Properties: Be careful when applying properties of square roots, especially with addition and subtraction. Remember that √(a + b) ≠ √a + √b.
- Ignoring Negative Signs: Remember that square roots can be both positive and negative. When solving equations, consider both solutions.
- Confusing Variables: When variables are involved, apply exponent rules correctly. For example, √(x^2) = |x|, not just x.
- Rushing the Process: Take your time to carefully work through each step. Rushing can lead to oversight and errors.
By being aware of these common mistakes and practicing regularly, you can improve your accuracy and confidence in simplifying square roots.
Advanced Techniques for Simplifying Square Roots
While basic techniques for simplifying square roots often suffice for straightforward problems, advanced techniques can help tackle more complex expressions and ensure efficiency. Below are some advanced methods and tips:
1. Rationalizing the Denominator
Rationalizing the denominator involves removing radicals from the denominator of a fraction. This is done by multiplying both the numerator and denominator by a suitable radical expression:
- For monomial denominators (e.g., ), multiply by the radical to make the denominator a perfect square: .
- For binomial denominators (e.g., ), multiply by the conjugate: .
2. Using Prime Factorization
Prime factorization involves breaking down the radicand into its prime factors to simplify the square root:
- Factor the number under the radical into its prime components.
- Pair up identical factors to move them outside the radical.
- Example: becomes .
3. Simplifying Radicals with Variables
When dealing with variables inside the radical, apply similar principles as with numbers:
- Simplify the coefficient and the variable separately.
- Use the property: .
- Example: .
4. Advanced Multiplication and Division of Radicals
When multiplying and dividing radical expressions, combine the radicands first and then simplify:
- Multiplication: .
- Division: .
5. Simplifying Nested Radicals
Nested radicals are expressions with radicals within radicals. Simplify them by working from the innermost radical outward:
- Example: .
- Rationalize the inner radical first and then proceed to the outer radical.
Practice Problems
- Simplify .
- Rationalize the denominator: .
- Simplify the nested radical: .

Practice Problems for Simplifying Square Roots
Here are some practice problems to help you master simplifying square roots. Try to follow each step carefully and verify your answers:
- Simplify \(\sqrt{50}\)
- Factor 50 into prime factors: \(50 = 2 \times 5 \times 5\)
- Group the pairs of prime factors: \(50 = (5 \times 5) \times 2\)
- Take the square root of the pair and simplify: \(\sqrt{50} = \sqrt{5^2 \times 2} = 5\sqrt{2}\)
- Simplify \(\sqrt{72}\)
- Factor 72 into prime factors: \(72 = 2 \times 2 \times 2 \times 3 \times 3\)
- Group the pairs of prime factors: \(72 = (2 \times 2) \times (3 \times 3) \times 2\)
- Take the square root of the pairs and simplify: \(\sqrt{72} = \sqrt{4 \times 9 \times 2} = 2 \times 3 \sqrt{2} = 6\sqrt{2}\)
- Simplify \(\sqrt{180}\)
- Factor 180 into prime factors: \(180 = 2 \times 2 \times 3 \times 3 \times 5\)
- Group the pairs of prime factors: \(180 = (2 \times 2) \times (3 \times 3) \times 5\)
- Take the square root of the pairs and simplify: \(\sqrt{180} = \sqrt{4 \times 9 \times 5} = 2 \times 3 \sqrt{5} = 6\sqrt{5}\)
- Simplify \(\sqrt{200}\)
- Factor 200 into prime factors: \(200 = 2 \times 2 \times 2 \times 5 \times 5\)
- Group the pairs of prime factors: \(200 = (2 \times 2) \times (5 \times 5) \times 2\)
- Take the square root of the pairs and simplify: \(\sqrt{200} = \sqrt{4 \times 25 \times 2} = 2 \times 5 \sqrt{2} = 10\sqrt{2}\)
- Simplify \(\sqrt{98}\)
- Factor 98 into prime factors: \(98 = 2 \times 7 \times 7\)
- Group the pairs of prime factors: \(98 = (7 \times 7) \times 2\)
- Take the square root of the pairs and simplify: \(\sqrt{98} = \sqrt{49 \times 2} = 7\sqrt{2}\)
Additional Practice Problems:
- Simplify \(\sqrt{32}\)
- Simplify \(\sqrt{75}\)
- Simplify \(\sqrt{150}\)
- Simplify \(\sqrt{24}\)
- Simplify \(\sqrt{48}\)
Remember to check each step of your simplification process to ensure accuracy. Practice makes perfect!
Conclusion and Tips for Mastery
Mastering the art of simplifying square roots can greatly enhance your mathematical skills and problem-solving abilities. Here are some key takeaways and tips to help you achieve proficiency:
- Understand the Basics: Ensure you have a solid understanding of what square roots are and why simplifying them is important.
- Learn the Methods: Familiarize yourself with various methods such as finding perfect square factors, prime factorization, and handling variables.
- Practice Regularly: Practice simplifying square roots regularly to reinforce your understanding and improve your speed.
- Memorize Perfect Squares: Memorizing common perfect squares up to a certain number can expedite the simplification process.
- Use Mathjax: Utilize Mathjax for writing and presenting mathematical expressions neatly and clearly.
- Review Examples: Study examples of both simple and complex square root simplifications to grasp different scenarios.
- Stay Organized: Maintain clarity and organization in your work, especially when dealing with fractions and variables.
- Seek Help When Needed: Don’t hesitate to seek help from teachers, peers, or online resources if you encounter challenging concepts.
- Apply in Real Life: Understand practical applications of simplified square roots in fields like engineering, physics, and finance.
- Avoid Common Mistakes: Be mindful of common errors such as misidentifying perfect squares or mishandling fractions.
By following these tips and consistently practicing, you will build confidence in handling square roots effectively and efficiently in various mathematical contexts.
Xem video này để học cách rút gọn căn bậc hai một cách hiệu quả. Có phù hợp với bài viết về đơn giản hóa căn bậc hai không?
Video Hướng Dẫn Cách Rút Gọn Căn Bậc Hai
READ MORE:
Xem video này để học cách rút gọn căn bậc hai cùng với Thầy J. Có phù hợp với bài viết về đơn giản hóa căn bậc hai không?
Rút Gọn Căn Bậc Hai | Toán với Thầy J