Topic square root of 45 simplified: Discover how to simplify the square root of 45 with our easy-to-follow, step-by-step guide. Uncover the prime factorization method and learn why simplifying square roots is useful in various practical applications. Avoid common mistakes and gain a deeper understanding of square roots to enhance your mathematical skills effortlessly.
Table of Content
- Square Root of 45 Simplified
- Introduction
- Understanding Square Roots
- Prime Factorization Method
- Simplifying Square Roots
- Step-by-Step Guide to Simplifying \(\sqrt{45}\)
- Why Simplify Square Roots?
- Common Mistakes to Avoid
- Practical Applications of Simplified Square Roots
- Frequently Asked Questions
- YOUTUBE: How to Simplify the Square Root of 45: sqrt(45)
Square Root of 45 Simplified
To simplify the square root of 45, we need to factor it into its prime factors and identify any perfect squares.
Step-by-Step Simplification
- First, find the prime factorization of 45:
- 45 ÷ 3 = 15
- 15 ÷ 3 = 5
- 5 is a prime number
So, the prime factorization of 45 is \(3^2 \times 5\).
- Next, express the square root of 45 in terms of its prime factors:
\(\sqrt{45} = \sqrt{3^2 \times 5}\)
- Then, separate the factors under the square root:
\(\sqrt{3^2 \times 5} = \sqrt{3^2} \times \sqrt{5}\)
- Simplify the square root of the perfect square:
\(\sqrt{3^2} = 3\)
Therefore, \(\sqrt{45} = 3\sqrt{5}\).
Conclusion
So, the simplified form of \(\sqrt{45}\) is \(3\sqrt{5}\).
| Expression | Simplified Form |
| \(\sqrt{45}\) | \(3\sqrt{5}\) |

READ MORE:
Introduction
The square root of 45 can be simplified to make calculations easier and more intuitive. This process involves expressing the square root in its simplest radical form. The square root of 45 is not a perfect square, which means it remains in its simplest form within a radical expression. Here, we will explore the steps to simplify the square root of 45 using prime factorization and other methods.
- Step 1: Factorize the number 45 into its prime factors. The prime factors of 45 are 3, 3, and 5.
- Step 2: Group the factors in pairs of identical numbers. In this case, we have a pair of 3s.
- Step 3: Simplify the expression by taking the square root of the paired factors. The square root of \(3^2\) is 3.
- Step 4: Multiply the simplified factors outside the radical with the remaining factors inside the radical. This gives us \(3\sqrt{5}\).
Thus, the simplified form of the square root of 45 is \(3\sqrt{5}\). This representation is useful in various mathematical computations and provides a clearer understanding of the number's properties.
Understanding Square Roots
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\). This concept is fundamental in mathematics and appears frequently in various applications, from geometry to algebra.
To understand square roots, it is essential to grasp a few key points:
- Radical Sign: The symbol for the square root is √, known as the radical sign. For example, the square root of 45 is written as \(\sqrt{45}\).
- Perfect Squares: A perfect square is a number that has an integer as its square root. Examples include 1, 4, 9, 16, and 25. For instance, 16 is a perfect square because its square root is 4 (\(4 \times 4 = 16\)).
- Non-Perfect Squares: Numbers that are not perfect squares have square roots that are irrational numbers (numbers that cannot be expressed as a simple fraction). For example, \(\sqrt{45}\) is an irrational number.
Square roots can be simplified by expressing the number inside the radical as a product of prime factors. Simplifying a square root means to make the number inside the radical as small as possible while still keeping it as a whole number.
Example of Simplifying a Square Root
Consider the square root of 45. To simplify \(\sqrt{45}\), follow these steps:
- Prime Factorization: Start by finding the prime factors of 45. The prime factors of 45 are 3, 3, and 5. So, \(45 = 3^2 \times 5\).
- Group the Factors: Group the prime factors into pairs. In this case, \(3^2\) forms a pair.
- Simplify: Take the square root of each pair of prime factors. The square root of \(3^2\) is 3. Therefore, \(\sqrt{45} = \sqrt{3^2 \times 5} = 3\sqrt{5}\).
Thus, the simplified form of \(\sqrt{45}\) is \(3\sqrt{5}\). This process helps in making complex calculations more manageable and is particularly useful in solving algebraic equations.
Understanding and simplifying square roots is a vital skill in mathematics, enabling more straightforward calculations and a deeper comprehension of numerical relationships.
Prime Factorization Method
The prime factorization method is a systematic way of simplifying square roots by breaking down the number into its prime factors. Here is a detailed step-by-step guide to understanding and applying the prime factorization method to simplify square roots:
- Prime Factorization:
Start by finding the prime factors of the number whose square root you want to simplify. Prime factors are the prime numbers that multiply together to give the original number.
For example, to find the prime factors of 45:
- 45 can be divided by 3 (the smallest prime number that can divide 45).
- \(45 \div 3 = 15\)
- 15 can also be divided by 3.
- \(15 \div 3 = 5\)
- 5 is a prime number.
Therefore, the prime factorization of 45 is:
\(45 = 3 \times 3 \times 5\)
- Pairing the Prime Factors:
Next, pair the same prime factors together. Each pair of identical prime factors represents a perfect square.
For 45, we have:
\(45 = 3 \times 3 \times 5\)
The pair of 3s forms a perfect square.
- Taking the Square Root of Each Pair:
Take one number from each pair of prime factors. This represents the square root of the perfect square formed by the pair.
From our example, the pair of 3s gives us a single 3:
\(\sqrt{3 \times 3} = 3\)
- Multiplying the Results:
Multiply the results from each pair of prime factors together. If there are any unpaired prime factors left, they remain under the square root symbol.
For 45, we have one 3 from the pair and one 5 left unpaired:
\(\sqrt{45} = 3 \times \sqrt{5}\)
Therefore, the simplified form of \(\sqrt{45}\) is:
\(\sqrt{45} = 3\sqrt{5}\)
Simplifying Square Roots
Simplifying square roots involves expressing the square root in its simplest radical form. This process helps to make complex square roots easier to work with. To simplify a square root, follow these steps:
- Prime Factorization:
Break down the number inside the square root into its prime factors. For example, for √45, we find the prime factors of 45, which are 3, 3, and 5. Thus, 45 = 3 × 3 × 5.
- Pairing Factors:
Group the prime factors into pairs. In the case of 45, we have a pair of 3s (3²) and a single 5. Therefore, √45 can be expressed as √(3² × 5).
- Simplifying the Radical:
Take the square root of the pairs and move them outside the radical. Since the square root of 3² is 3, we can simplify √(3² × 5) to 3√5. Thus, the simplified form of √45 is 3√5.
This method can be applied to any number to simplify its square root. Here are additional examples:
- Example 1: Simplify √12
12 can be factored into 4 and 3. Therefore, √12 = √(4 × 3) = √4 × √3 = 2√3.
- Example 2: Simplify √18
18 can be factored into 9 and 2. Therefore, √18 = √(9 × 2) = √9 × √2 = 3√2.
By following these steps, you can simplify any square root, making it easier to work with in mathematical equations and applications.

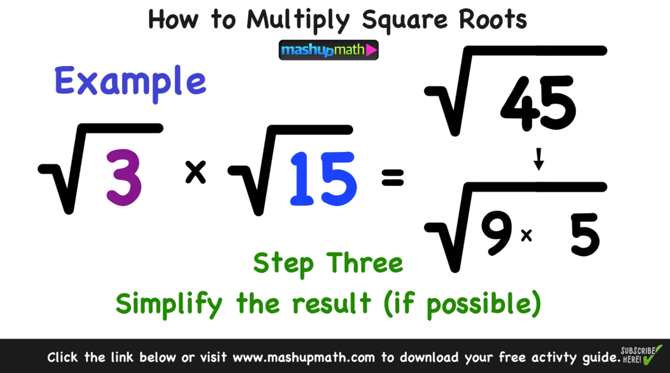
Step-by-Step Guide to Simplifying \(\sqrt{45}\)
In this section, we will go through a detailed, step-by-step guide on how to simplify the square root of 45. The goal is to express \(\sqrt{45}\) in its simplest radical form.
-
List the factors of 45:
The factors of 45 are: 1, 3, 5, 9, 15, and 45.
-
Identify the perfect squares:
From the list of factors, the perfect squares are: 1 and 9.
-
Divide by the largest perfect square:
Divide 45 by the largest perfect square from the previous step:
\[
\frac{45}{9} = 5
\] -
Calculate the square root of the largest perfect square:
The square root of 9 is 3:
\[
\sqrt{9} = 3
\] -
Combine the results:
Put steps 3 and 4 together to get the simplified form of the square root:
\[
\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}
\]
Thus, the simplified form of \(\sqrt{45}\) is \(3\sqrt{5}\).
Why Simplify Square Roots?
Simplifying square roots is a crucial skill in mathematics that offers several benefits:
- Ease of Calculation: Simplified square roots make it easier to perform arithmetic operations. For example, dealing with \(3\sqrt{5}\) is often simpler than working with \(\sqrt{45}\).
- Improved Understanding: Simplifying square roots helps in understanding the properties and behaviors of numbers. Recognizing patterns in factorization enhances mathematical intuition.
- Standard Form: Many mathematical problems and solutions are presented in their simplest form. This standardization helps in comparing and contrasting results effectively.
- Accuracy: Working with simplified square roots reduces the chance of errors in calculations, especially when dealing with irrational numbers.
- Application in Formulas: Simplified square roots are often required in various formulas and equations in algebra, geometry, and calculus. This simplification aids in the practical application of these formulas.
- Educational Importance: Learning to simplify square roots reinforces fundamental concepts such as prime factorization, properties of exponents, and the nature of irrational numbers.
In summary, simplifying square roots is not just about making numbers look neater; it plays a significant role in enhancing mathematical comprehension and accuracy.
Common Mistakes to Avoid
Simplifying square roots can be straightforward, but certain mistakes are common. Here are some pitfalls to watch out for:
- Incorrect Prime Factorization:
Ensure the number is broken down correctly into its prime factors. For example, 45 should be factored as \(3^2 \times 5\). Errors in this step lead to incorrect simplification.
- Forgetting to Simplify Completely:
Make sure to simplify as much as possible. For \( \sqrt{45} \), simplifying to \( 3\sqrt{5} \) is necessary rather than leaving it as \( \sqrt{9 \times 5} \).
- Mistaking Multiplication for Addition:
When dealing with square roots, remember that multiplication inside the radical is different from addition. For instance, \( \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5} \), not \( \sqrt{9 + 5} \).
- Not Checking for Perfect Squares:
Always look for perfect squares in the factorization. In \( \sqrt{45} \), recognizing that 9 is a perfect square allows simplification to \( 3\sqrt{5} \).
- Incorrectly Handling Negative Radicals:
Square roots of negative numbers require the use of imaginary numbers. For example, \( \sqrt{-45} = 3i\sqrt{5} \), not \( 3\sqrt{-5} \).
- Improper Simplification of Radical Expressions:
Ensure the correct steps are followed for each term under the radical. Missteps can lead to incorrect answers. Always double-check your work for accuracy.
Avoiding these common mistakes will help ensure you simplify square roots accurately and effectively.
Practical Applications of Simplified Square Roots
Simplifying square roots is not just an abstract mathematical exercise; it has practical applications in various fields. Here are some key areas where simplified square roots are useful:
-
Geometry and Area Calculations
In geometry, square roots are used to find the side length of a square when its area is known. For example, if a square has an area of 45 square units, the length of each side is \(\sqrt{45}\), which simplifies to \(3\sqrt{5}\).
-
Physics and Engineering
Square roots appear frequently in physics, particularly in formulas involving gravitational force, electrical fields, and sound waves. For instance, the inverse-square law, which states that the intensity of a physical quantity (like light or sound) diminishes with the square of the distance from the source, involves square roots.
-
Statistics and Probability
In statistics, the standard deviation, which measures the amount of variation or dispersion in a set of values, is calculated using square roots. Simplifying these calculations can make it easier to understand and apply statistical data.
-
Everyday Problem Solving
Simplified square roots are also useful in everyday situations. For example, when figuring out the dimensions of materials needed for a project, or when working out the correct proportions in a recipe, understanding how to simplify square roots can provide quick and accurate answers.
By mastering the simplification of square roots, you can enhance your problem-solving skills and apply mathematical principles more effectively in real-world scenarios.
Frequently Asked Questions
-
What is the square root of 45?
The square root of 45 is approximately 6.708, which is an irrational number.
-
What is the square root of 45 in its simplest form?
The square root of 45 in its simplest radical form is \(3\sqrt{5}\).
-
Is the square root of 45 a rational or irrational number?
The square root of 45 is an irrational number because it cannot be expressed as a simple fraction.
-
How do you simplify the square root of 45?
To simplify \(\sqrt{45}\), you can use prime factorization:
- Find the prime factors of 45: \(45 = 3 \times 3 \times 5\).
- Group the factors into pairs: \(45 = 3^2 \times 5\).
- Simplify the expression by taking the square root of the pairs: \(\sqrt{45} = \sqrt{3^2 \times 5} = 3\sqrt{5}\).
Can the value of a square root be negative?
Yes, square roots can be both positive and negative because both \((+6.708)^2\) and \((-6.708)^2\) equal 45. However, the principal (default) square root is positive.
-
Is \(\sqrt{-45}\) a real number?
No, \(\sqrt{-45}\) is not a real number because the square root of a negative number results in an imaginary number. In this case, \(\sqrt{-45} = 3i\sqrt{5}\), where \(i\) is the imaginary unit.










