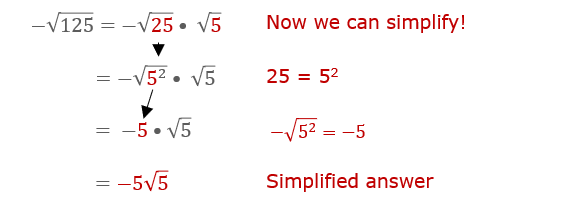Topic square root of 48 in simplest radical form: Discover the steps to simplify the square root of 48 into its simplest radical form. This article covers methods like prime factorization, long division, and the Babylonian method, offering a thorough understanding of how to handle this common mathematical problem.
Table of Content
- Square Root of 48 in Simplest Radical Form
- Introduction
- Understanding Square Roots
- Definition and Properties of Square Roots
- Prime Factorization Method
- Step-by-Step Process to Simplify Square Roots
- Grouping and Pairing Factors
- Simplifying the Radical Expression
- Final Simplified Form
- Applications and Examples
- Practice Problems
- Common Mistakes to Avoid
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Tìm hiểu cách đơn giản hóa căn bậc hai của 48 với hướng dẫn chi tiết và dễ hiểu. Video hướng dẫn từng bước giúp bạn nắm vững kiến thức.
Square Root of 48 in Simplest Radical Form
The square root of 48 can be simplified by breaking it down into its prime factors.
Steps to Simplify
- Find the prime factorization of 48.
- Group the prime factors into pairs.
- Simplify the expression by taking out pairs of prime factors from under the radical sign.
Prime Factorization of 48
The prime factorization of 48 is:
\[ 48 = 2 \times 24 \]
\[ 48 = 2 \times 2 \times 12 \]
\[ 48 = 2 \times 2 \times 2 \times 6 \]
\[ 48 = 2 \times 2 \times 2 \times 2 \times 3 \]
Grouping the Factors
We can group the prime factors into pairs:
\[ 48 = (2 \times 2) \times (2 \times 2) \times 3 \]
\]
\[ 48 = 2^2 \times 2^2 \times 3 \]
\]
Simplifying the Radical
Take out the pairs of 2s from under the radical sign:
\[ \sqrt{48} = \sqrt{2^2 \times 2^2 \times 3} \]
\[ \sqrt{48} = 2 \times 2 \times \sqrt{3} \]
\[ \sqrt{48} = 4 \sqrt{3} \]
Therefore, the square root of 48 in simplest radical form is \(4 \sqrt{3}\).

READ MORE:
Introduction
In this guide, we will explore how to simplify the square root of 48 to its simplest radical form. Simplifying square roots is a fundamental skill in algebra that allows us to express roots in a more manageable and interpretable format. Understanding the process and the steps involved will help you tackle more complex mathematical problems with confidence.
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\). However, not all square roots result in whole numbers. When we encounter such cases, we use the radical form to express the square root. The goal is to simplify the expression under the radical sign as much as possible.
In this document, we will:
- Define and discuss the properties of square roots
- Introduce the prime factorization method as a tool for simplification
- Provide a step-by-step process to simplify the square root of 48
- Demonstrate the application of these steps through examples
- Offer practice problems for further learning
- Highlight common mistakes and how to avoid them
By the end of this guide, you will have a solid understanding of how to simplify the square root of 48 and apply these techniques to other square roots.
Understanding Square Roots
The concept of square roots is fundamental in mathematics and has a wide range of applications. A square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). In other words, \(y\) is the number that, when multiplied by itself, results in \(x\).
For example, the square root of 16 is 4, because \(4 \times 4 = 16\). Not all numbers are perfect squares, meaning their square roots are not whole numbers. For instance, the square root of 48 is not an integer.
Square roots can be represented using the radical symbol \(\sqrt{}\). The number under the radical symbol is called the radicand. For example, in \(\sqrt{48}\), 48 is the radicand.
Here are some important properties of square roots:
- Non-negative: The principal square root of a non-negative number is also non-negative. For any real number \(x \geq 0\), \(\sqrt{x} \geq 0\).
- Product Property: The square root of a product is the product of the square roots. \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\).
- Quotient Property: The square root of a quotient is the quotient of the square roots. \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), where \(b \neq 0\).
- Perfect Squares: If a number is a perfect square, its square root is an integer. For example, \(\sqrt{25} = 5\) because \(25 = 5 \times 5\).
- Irrational Roots: The square roots of non-perfect squares are irrational numbers, meaning they cannot be expressed as simple fractions. For example, \(\sqrt{48}\) is irrational.
Understanding these properties helps in simplifying expressions involving square roots and in solving equations that include them. In the context of our topic, simplifying the square root of 48, we'll use these properties to break down the problem into manageable steps.
Definition and Properties of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol (√). For example, the square root of 48 is written as √48.
Square roots have several important properties:
- Non-negative Results: The principal square root of a non-negative number is non-negative. This means that for any non-negative number \(a\), the square root √\(a\) is also non-negative.
- Product Property: The square root of a product is equal to the product of the square roots of the factors. Mathematically, √\(ab\) = √\(a\) * √\(b\).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and denominator. Mathematically, √\(\frac{a}{b}\) = \(\frac{√a}{√b}\) for any non-negative numbers \(a\) and \(b\) (where \(b ≠ 0\)).
- Power Property: The square root of a number raised to a power is equal to the number raised to half that power. For example, √\(a^2\) = \(a^{\frac{1}{2}}\).
When simplifying square roots, the goal is to express the radical in its simplest form. This often involves factoring the number under the radical into its prime factors and then simplifying by pairing identical factors.
Let's illustrate these properties with an example:
- Prime Factorization: To simplify √48, we first find the prime factorization of 48: 48 = 2 × 2 × 2 × 2 × 3 = \(2^4 \times 3\).
- Grouping Factors: We group the prime factors into pairs: \((2 \times 2) \times (2 \times 2) \times 3\).
- Extracting Pairs: Each pair of 2's can be taken out of the radical: √(2 × 2 × 2 × 2 × 3) = 2 × 2 √3 = 4√3.
Thus, the square root of 48 simplified is 4√3.
Prime Factorization Method
The prime factorization method is a useful technique to simplify square roots. This method involves breaking down the number into its prime factors and then simplifying the radical expression. Let's apply this method to simplify the square root of 48.
-
List the Prime Factors of 48:
First, we need to find the prime factors of 48. The prime factorization of 48 is:
\[
48 = 2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3
\] -
Pair the Prime Factors:
Next, we pair the identical prime factors. In this case, we have four 2's, which can be paired as:
\[
48 = (2 \times 2) \times (2 \times 2) \times 3
\] -
Simplify the Expression:
Each pair of prime factors can be taken out of the radical as a single number. Thus, we take the pairs of 2's out:
\[
\sqrt{48} = \sqrt{(2 \times 2) \times (2 \times 2) \times 3} = 2 \times 2 \times \sqrt{3} = 4\sqrt{3}
\]
Therefore, the simplest radical form of the square root of 48 is \( 4\sqrt{3} \).
This method of using prime factorization helps us break down the number and easily identify the factors that can be simplified out of the radical.
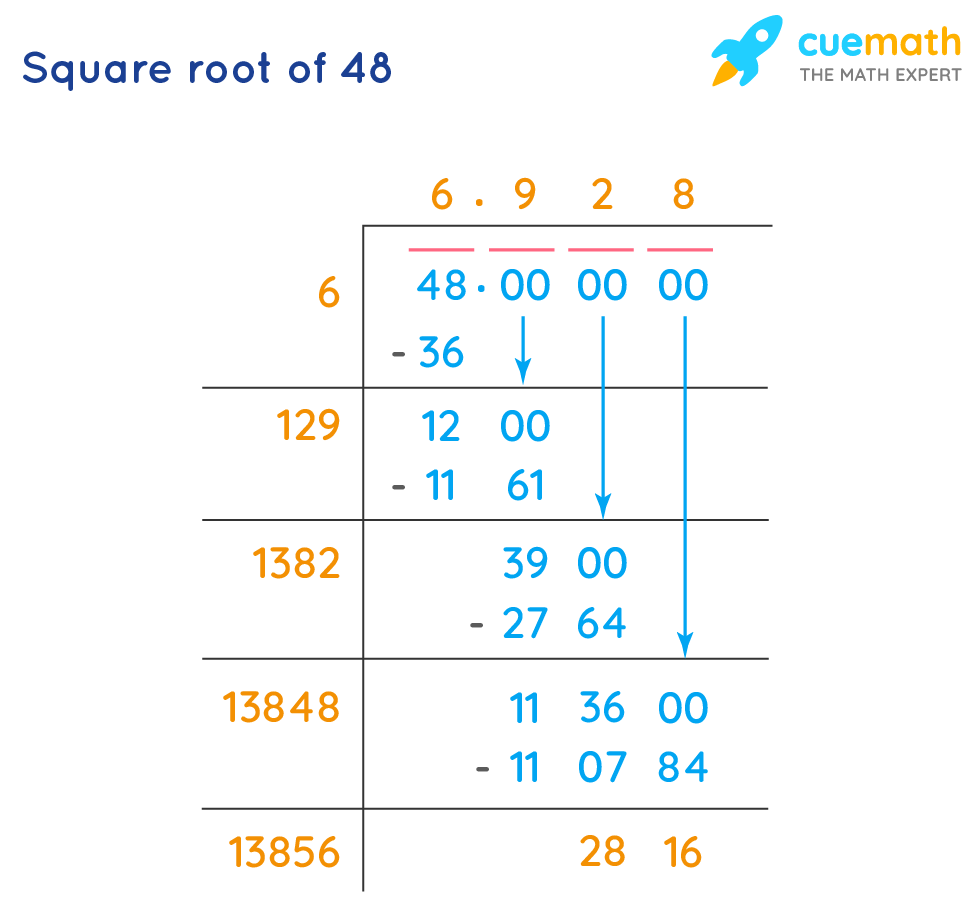
Step-by-Step Process to Simplify Square Roots
Simplifying square roots involves a few straightforward steps. Here, we'll demonstrate this process using the square root of 48.
-
Prime Factorization: First, find the prime factors of the number under the square root. For 48, the prime factors are:
48 = 2 × 2 × 2 × 2 × 3
-
Group the Prime Factors: Group the prime factors in pairs:
(2 × 2) × (2 × 2) × 3
-
Take Out the Pairs: For each pair of identical factors, take one factor out of the square root:
√(2 × 2) × √(2 × 2) × √3 = 2 × 2 × √3
-
Simplify the Expression: Multiply the numbers outside the radical:
2 × 2 × √3 = 4√3
-
Final Simplified Form: Therefore, the simplified form of √48 is:
√48 = 4√3
This process can be applied to any number to simplify its square root. By following these steps, you can break down the problem and make it more manageable.
Grouping and Pairing Factors
To simplify the square root of 48, we need to group and pair its prime factors. Here's how we do it step by step:
First, write down the prime factorization of 48:
\[ 48 = 2 \times 2 \times 2 \times 2 \times 3 \]
Next, we group the identical prime factors into pairs:
\[ 48 = (2 \times 2) \times (2 \times 2) \times 3 \]
Each pair of identical factors can be taken out from under the square root:
\[ \sqrt{48} = \sqrt{(2 \times 2) \times (2 \times 2) \times 3} \]
Simplify the expression by taking each pair of identical factors out of the radical:
\[ \sqrt{(2 \times 2) \times (2 \times 2) \times 3} = 2 \times 2 \times \sqrt{3} \]
Multiply the numbers outside the radical to get the final simplified form:
\[ 2 \times 2 \times \sqrt{3} = 4\sqrt{3} \]
So, the square root of 48 in simplest radical form is \(4\sqrt{3}\).
Simplifying the Radical Expression
To simplify the square root of 48, we can use the prime factorization method. This involves expressing the number under the square root as a product of its prime factors and then simplifying. Here are the steps:
- First, perform the prime factorization of 48:
- 48 can be factored as \(48 = 2 \times 24\)
- 24 can be factored as \(24 = 2 \times 12\)
- 12 can be factored as \(12 = 2 \times 6\)
- 6 can be factored as \(6 = 2 \times 3\)
Thus, the prime factorization of 48 is \(48 = 2^4 \times 3\).
- Next, group the prime factors into pairs:
- The prime factors of 48 are \(2 \times 2 \times 2 \times 2 \times 3\).
- We can group these as \((2 \times 2) \times (2 \times 2) \times 3\).
- This simplifies to \((2^2) \times (2^2) \times 3\).
- Then, simplify the square root by taking one number from each pair of identical factors:
- \(\sqrt{(2^2) \times (2^2) \times 3} = 2 \times 2 \times \sqrt{3}\).
- Finally, multiply the numbers outside the radical:
- This gives us \(4 \sqrt{3}\).
Thus, the square root of 48 in simplest radical form is \(4 \sqrt{3}\).
Final Simplified Form
To simplify the square root of 48, we follow the prime factorization method and identify the simplest radical form. Here's a detailed breakdown of the process:
-
First, we factorize 48 into its prime factors:
\( 48 = 2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3 \)
-
Next, we group the factors into pairs:
\( 48 = (2 \times 2) \times (2 \times 2) \times 3 = 4 \times 4 \times 3 \)
-
Now, we take the square root of each group of pairs:
\( \sqrt{48} = \sqrt{4 \times 4 \times 3} = 4\sqrt{3} \)
Thus, the final simplified form of the square root of 48 is:
\[ \sqrt{48} = 4\sqrt{3} \]
This form is the simplest radical form, where 4 is the integer outside the radical, and 3 remains inside the radical.

Applications and Examples
The simplified form of the square root of 48, which is \(4\sqrt{3}\), can be applied in various real-world scenarios and mathematical contexts. Here are some examples:
Applications
- Geometry: In geometry, the square root of 48 can be used to find the length of the diagonal of a rectangle with sides 4 units and 8 units using the Pythagorean theorem.
- Engineering: Engineers might use the square root of 48 in calculations involving square roots and radical expressions when designing structures or mechanical components.
- Physics: The square root of 48 can be involved in physical calculations, such as determining the magnitude of a vector in a coordinate system.
Examples
Here are some practical examples that demonstrate the use of the square root of 48:
- Diagonal of a Rectangle: Consider a rectangle with sides of 4 units and 8 units. The length of the diagonal \(d\) can be found using the Pythagorean theorem: \[ d = \sqrt{4^2 + 8^2} = \sqrt{16 + 64} = \sqrt{80} = 4\sqrt{5} \] Here, we simplified \(\sqrt{80}\) to \(4\sqrt{5}\), showing the practical use of simplifying radicals.
- Scaling Factors: In scaling models or drawings, if a scale factor involves \(\sqrt{48}\), it simplifies to \(4\sqrt{3}\). This simplification makes calculations easier and more intuitive.
Practice Problems
To solidify your understanding, try solving these practice problems:
- Simplify \(\sqrt{75}\) and use it in a geometry problem to find the length of the diagonal of a square with side length 5 units.
- Use the simplified form of \(\sqrt{48}\) to solve for the hypotenuse of a right triangle with legs measuring 6 units and 8 units.
By practicing these applications and examples, you can gain a deeper understanding of how to use simplified radical forms in various mathematical and real-world contexts.
Practice Problems
Practice simplifying square roots by working through the following problems. Each problem will help reinforce your understanding of the process and ensure you can apply the methods correctly.
-
Simplify \( \sqrt{72} \).
Solution:
- Prime factorization of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Group pairs of the same factors: \( (2 \times 2) \times 2 \times (3 \times 3) \).
- Take one number from each pair outside the radical: \( 2 \times 3 \sqrt{2} = 6\sqrt{2} \).
-
Simplify \( \sqrt{50} \).
Solution:
- Prime factorization of 50: \( 50 = 2 \times 5 \times 5 \).
- Group pairs of the same factors: \( 2 \times (5 \times 5) \).
- Take one number from each pair outside the radical: \( 5 \sqrt{2} \).
-
Simplify \( \sqrt{98} \).
Solution:
- Prime factorization of 98: \( 98 = 2 \times 7 \times 7 \).
- Group pairs of the same factors: \( 2 \times (7 \times 7) \).
- Take one number from each pair outside the radical: \( 7 \sqrt{2} \).
-
Simplify \( \sqrt{200} \).
Solution:
- Prime factorization of 200: \( 200 = 2 \times 2 \times 2 \times 5 \times 5 \).
- Group pairs of the same factors: \( (2 \times 2) \times 2 \times (5 \times 5) \).
- Take one number from each pair outside the radical: \( 2 \times 5 \sqrt{2} = 10\sqrt{2} \).
-
Simplify \( \sqrt{128} \).
Solution:
- Prime factorization of 128: \( 128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \).
- Group pairs of the same factors: \( (2 \times 2) \times (2 \times 2) \times (2 \times 2) \times 2 \).
- Take one number from each pair outside the radical: \( 2 \times 2 \times 2 \sqrt{2} = 8\sqrt{2} \).
Common Mistakes to Avoid
When simplifying the square root of 48, it's important to be aware of common mistakes to avoid. Here are some key points to keep in mind:
- Incorrect Factorization: Ensure you correctly factorize the number. The prime factorization of 48 is \(2^4 \times 3\). Any error in this step will lead to an incorrect simplified form.
- Ignoring Pairs of Factors: When simplifying, always group the factors into pairs. For example, with 48, you have \(2 \times 2\) and another \(2 \times 2\). Don't miss out on pairing correctly.
- Incorrectly Simplifying the Radical: Make sure to take the square root of each pair. For \( \sqrt{48} \), the pairs are \( (2 \times 2) \) and \( (2 \times 2) \), which simplifies to \( 2 \times 2 = 4 \). So, \( \sqrt{48} = 4\sqrt{3} \).
- Forgetting the Remaining Factors: After taking the pairs out of the square root, don't forget any remaining factors. In \( \sqrt{48} \), after extracting pairs of 2s, the factor 3 remains under the square root.
- Mathematical Errors: Double-check your calculations at each step. A small arithmetic error can lead to an incorrect final result.
By being mindful of these common mistakes, you can ensure that you correctly simplify the square root of 48 to its simplest radical form, which is \( 4\sqrt{3} \).
Frequently Asked Questions
-
What is the square root of 48?
The square root of 48 is approximately 6.928. In its simplest radical form, it is expressed as \(4\sqrt{3}\).
-
Can we find the square root of 48 by the approximation method?
Yes, you can estimate the square root of 48 using the approximation method. This method involves finding the two consecutive perfect squares between which 48 lies, and then estimating the value.
-
How do you find the square root of 48?
You can find the square root of 48 using the prime factorization method, the repeated subtraction method, or the long division method.
-
Is the square root of 48 an irrational number?
Yes, the square root of 48 is an irrational number because it cannot be expressed as a simple fraction.
-
What is the square root of 48 in simplified form?
The square root of 48 in simplified form is \(4\sqrt{3}\).
-
How do you simplify the square root of 48?
To simplify the square root of 48, find the prime factorization of 48, which is \(2^4 \times 3\). Group the prime factors into pairs: \( (2 \times 2) \times (2 \times 2) \times 3 \). Simplify by taking one factor out of each pair: \( 2 \times 2 \times \sqrt{3} = 4\sqrt{3} \).

Conclusion
Understanding and simplifying the square root of 48 into its simplest radical form, \(4\sqrt{3}\), provides a solid foundation for further mathematical learning and application. This process not only reinforces essential algebraic concepts but also enhances problem-solving skills, which are critical in various real-world scenarios and advanced mathematical studies.
Throughout this guide, we have explored the step-by-step methods for simplifying square roots, including prime factorization and the identification of perfect squares within the radicand. By mastering these techniques, you can approach similar problems with confidence and precision.
Remember, simplifying radicals is a fundamental skill in algebra that paves the way for more complex mathematical operations. Whether you are a student seeking to excel in your coursework or an enthusiast aiming to deepen your mathematical knowledge, practicing these concepts will undoubtedly contribute to your success.
We hope this comprehensive guide on the square root of 48 has been informative and helpful. Continue to practice and explore other mathematical challenges to further enhance your skills and understanding. Happy learning!
Tìm hiểu cách đơn giản hóa căn bậc hai của 48 với hướng dẫn chi tiết và dễ hiểu. Video hướng dẫn từng bước giúp bạn nắm vững kiến thức.
Học Cách Đơn Giản Hóa Căn Bậc Hai Của 48
READ MORE:
Tìm hiểu cách đơn giản hóa căn bậc hai của 48: Sqrt(48) với hướng dẫn chi tiết và dễ hiểu. Video hướng dẫn từng bước giúp bạn nắm vững kiến thức.
Cách Đơn Giản Hóa Căn Bậc Hai Của 48: Sqrt(48)