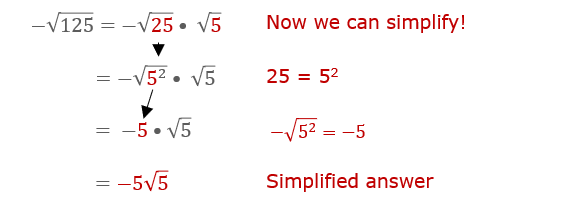Topic square root calculator radical form: Discover the power of a square root calculator for simplifying radical expressions! This handy tool helps you find exact square roots in radical form, making complex calculations straightforward and easy to understand. Perfect for students and math enthusiasts, this calculator is an essential resource for mastering square root operations and enhancing your mathematical skills.
Table of Content
- Square Root Calculator - Radical Form
- Introduction to Square Root Calculators
- How to Use a Square Root Calculator
- Step-by-Step Instructions
- Simplifying Square Roots
- Square Root Simplification Rules
- Examples of Square Root Calculations
- Perfect Squares and Their Roots
- Complex and Imaginary Square Roots
- Fractional Exponents and Square Roots
- Advanced Square Root Operations
- Applications of Square Root Calculators
- Frequently Asked Questions
- Additional Resources
- YOUTUBE: Simplifying square roots with a graphing calculator
Square Root Calculator - Radical Form
Below is a square root calculator that provides results in radical form:
| Number | Square Root (Radical Form) |
| √2 | 1.414 |
| √3 | 1.732 |
| √5 | 2.236 |
| √6 | 2.449 |
This calculator provides approximate values for commonly used square roots. For more precise calculations, consider using a scientific calculator or software.

READ MORE:
Introduction to Square Root Calculators
Square root calculators are essential tools for simplifying and understanding the square roots of both positive and negative numbers. They can reduce square roots to their simplest radical form and also provide approximate decimal values. Whether dealing with whole numbers, fractions, or complex numbers, these calculators help in breaking down and simplifying the expressions under the radical sign.
Understanding the rules and steps involved in simplifying square roots is crucial. Typically, the simplification process involves finding factors of the radicand (the number under the square root) and identifying any perfect square factors. This method can be applied to both simple and complex numbers, making square root calculators versatile tools in both basic and advanced mathematical computations.
- Step 1: Identify the radicand and check if it has any perfect square factors.
- Step 2: Use the property \( \sqrt{x \times y} = \sqrt{x} \times \sqrt{y} \) to separate the radicand into two factors, one of which is a perfect square.
- Step 3: Simplify the square root of the perfect square factor.
- Step 4: Multiply the simplified square root by the square root of the remaining factor.
For example, to simplify \( \sqrt{27} \):
- Identify factors: 27 can be factored into 9 and 3, where 9 is a perfect square.
- Apply the property: \( \sqrt{27} = \sqrt{9 \times 3} = \sqrt{9} \times \sqrt{3} \).
- Simplify: \( \sqrt{9} = 3 \), so \( \sqrt{27} = 3\sqrt{3} \).
Square root calculators not only simplify the radical form but also handle operations such as addition, subtraction, multiplication, and division of square roots. This functionality makes them indispensable for students, teachers, and professionals dealing with algebraic expressions and complex numbers.
How to Use a Square Root Calculator
A square root calculator simplifies the process of finding the square root of a given number. Here's a step-by-step guide on how to use a square root calculator:
- Enter the Number:
Input the number for which you want to find the square root into the calculator. This number can be positive or negative.
- Select the Operation:
Choose the "Calculate the Square Root" option. This ensures the calculator understands that you need the square root and not another operation.
- Submit the Input:
Click the "Calculate" button or the equivalent to process the entered number. The calculator will then compute the square root.
- View the Results:
The calculator will display the square root in two forms:
- Exact Form: This form shows the simplified radical expression. For instance, the square root of 50 will be displayed as \( \sqrt{50} = 5\sqrt{2} \).
- Decimal Form: This form provides the decimal approximation of the square root, which is useful for practical calculations.
- Check for Perfect Squares:
If the entered number is a perfect square, the result will be a whole number. For example, the square root of 49 will be shown as \( \sqrt{49} = 7 \).
- Complex Numbers:
If the input is a negative number, the calculator will display the result as a complex number. For instance, the square root of -25 will be shown as \( \sqrt{-25} = 5i \).
Using a square root calculator simplifies the process of finding square roots, ensuring both accurate and quick results. This tool is essential for students, engineers, and anyone dealing with mathematical computations.
Step-by-Step Instructions
Using a square root calculator is a straightforward process that involves entering the number you want to find the square root of and interpreting the results. Here are the detailed steps:
- Open the square root calculator on your chosen platform, such as Mathway, CalculatorSoup, or Symbolab.
- Enter the number you want to find the square root of in the provided input field.
- Click the "Calculate" or equivalent button to submit the number.
- The calculator will display the square root of the number. If the number is a perfect square, the result will be in exact form. Otherwise, it will show both an exact form and a decimal approximation.
- For more complex calculations, some calculators allow additional functions such as simplifying radicals or finding imaginary roots for negative numbers.
Here's a quick reference table for some common inputs and outputs:
| Input | Exact Form | Decimal Approximation |
|---|---|---|
| 4 | \(\sqrt{4} = 2\) | 2.0 |
| 9 | \(\sqrt{9} = 3\) | 3.0 |
| 10 | \(\sqrt{10} = \sqrt{10}\) | 3.162 |
| -16 | \(\sqrt{-16} = 4i\) | N/A |
Follow these steps to efficiently use any square root calculator and interpret the results accurately for both real and complex numbers.
Simplifying Square Roots
Simplifying square roots involves reducing the expression under the square root (the radicand) to its simplest form. Here is a step-by-step guide to help you simplify square roots effectively.
-
Find the prime factors of the radicand:
Break down the number inside the square root into its prime factors. For example, for √50, you would find that 50 = 2 × 5 × 5.
-
Pair the prime factors:
Group the prime factors into pairs. For √50, the prime factors are 2 and 5². Since 5² forms a pair, it can be simplified.
-
Simplify the pairs:
Move each pair of prime factors outside the square root as a single number. For √50, 5² becomes 5 outside the square root, leaving √2 inside. Thus, √50 simplifies to 5√2.
-
Combine the simplified factors:
Write the simplified expression by combining the numbers outside the square root with the remaining radicand. For example, 5√2 is the simplified form of √50.
By following these steps, you can simplify any square root to its radical form. This process is useful for making calculations easier and for recognizing patterns in algebraic expressions.
Square Root Simplification Rules
Understanding the rules for simplifying square roots is essential for efficient calculation. Here are the key rules to follow:
- Identify and extract perfect squares: Determine the largest perfect square factor of the radicand (the number under the square root) and rewrite the square root as the product of the square root of this factor and the square root of the remaining factor.
- Use the product rule for square roots: The square root of a product is equal to the product of the square roots of the factors. For example, \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Use the quotient rule for square roots: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. For example, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Simplify square roots of fractions: Apply the quotient rule and simplify the square root of both the numerator and the denominator.
By following these rules, you can simplify square roots efficiently and accurately, making complex calculations more manageable.
Examples of Square Root Calculations
Square root calculations can range from simple to complex, depending on the numbers involved. Here are a few examples to illustrate different scenarios:
-
Example 1: Simple Square Root
Calculate the square root of 25.
\[
\sqrt{25} = 5
\] -
Example 2: Square Root of a Fraction
Calculate the square root of \(\frac{1}{4}\).
\[
\sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2}
\] -
Example 3: Square Root of a Negative Number
Calculate the square root of -9.
\[
\sqrt{-9} = 3i
\]Note: \(i\) is the imaginary unit where \(i^2 = -1\).
-
Example 4: Square Root of a Non-Perfect Square
Calculate the square root of 20.
\[
\sqrt{20} = \sqrt{4 \times 5} = \sqrt{4} \times \sqrt{5} = 2\sqrt{5}
\] -
Example 5: Simplifying Radicals
Simplify \(\sqrt{72}\).
\[
\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}
\] -
Example 6: Product of Square Roots
Calculate \(\sqrt{2} \times \sqrt{8}\).
\[
\sqrt{2} \times \sqrt{8} = \sqrt{2 \times 8} = \sqrt{16} = 4
\]
Perfect Squares and Their Roots
Perfect squares are numbers that have integer square roots. This means that when you take the square root of a perfect square, you get a whole number without any decimal or fractional part. Understanding perfect squares can make working with square roots much easier.
Below is a list of some common perfect squares and their roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
To find the square root of a perfect square, you can use the property that if \( a^2 = b \), then \( a \) is the square root of \( b \). For example, since \( 3^2 = 9 \), the square root of 9 is 3.
Using a square root calculator, you can easily determine whether a number is a perfect square and find its square root. Simply enter the number, and the calculator will provide the square root if it is a perfect square.
Complex and Imaginary Square Roots
Understanding complex and imaginary square roots is crucial when dealing with negative radicands. This section will guide you through the process of finding and simplifying these roots.
Complex numbers are of the form \( a + bi \), where \( i \) is the imaginary unit defined as \( \sqrt{-1} \). Here are the steps to calculate complex and imaginary square roots:
- Identify the negative radicand. For example, consider \( \sqrt{-9} \).
- Rewrite the negative radicand using the imaginary unit \( i \). For \( \sqrt{-9} \), we rewrite it as \( \sqrt{9 \cdot -1} \).
- Separate the square roots: \( \sqrt{9} \cdot \sqrt{-1} \).
- Simplify the square roots: \( 3 \cdot i \).
- Thus, \( \sqrt{-9} = 3i \).
Here's another example for a better understanding:
- Consider \( \sqrt{-16} \).
- Rewrite as \( \sqrt{16 \cdot -1} \).
- Separate: \( \sqrt{16} \cdot \sqrt{-1} \).
- Simplify: \( 4 \cdot i \).
- So, \( \sqrt{-16} = 4i \).
For more complex numbers, consider the general form \( a + bi \). For instance:
- Calculate \( \sqrt{-25} \):
- Rewrite as \( \sqrt{25 \cdot -1} \).
- Separate: \( \sqrt{25} \cdot \sqrt{-1} \).
- Simplify: \( 5 \cdot i \).
- Thus, \( \sqrt{-25} = 5i \).
Complex roots can also appear in quadratic equations where the discriminant is negative. For example:
- Consider the equation \( x^2 + 4 = 0 \).
- Solve for \( x^2 = -4 \).
- Take the square root: \( x = \pm \sqrt{-4} \).
- Simplify: \( x = \pm 2i \).
Understanding these steps helps in simplifying complex and imaginary square roots, making complex mathematical problems more manageable.

Fractional Exponents and Square Roots
Understanding the relationship between fractional exponents and square roots is essential in mathematics. Fractional exponents provide an alternative way of expressing roots, which can simplify many algebraic expressions and calculations.
The general form of a fractional exponent is:
\(a^{\frac{m}{n}} = \sqrt[n]{a^m} = (\sqrt[n]{a})^m\)
For example:
- \(a^{\frac{1}{2}} = \sqrt{a}\)
- \(a^{\frac{1}{3}} = \sqrt[3]{a}\) (cube root of a)
- \(a^{\frac{2}{3}} = (\sqrt[3]{a})^2 = \sqrt[3]{a^2}\)
Let's go through the steps to simplify expressions with fractional exponents:
1. Converting Radicals to Fractional Exponents
To convert a radical to a fractional exponent, use the following formula:
\(\sqrt[n]{a^m} = a^{\frac{m}{n}}\)
Examples:
- \(\sqrt{a} = a^{\frac{1}{2}}\)
- \(\sqrt[3]{a^2} = a^{\frac{2}{3}}\)
2. Simplifying Expressions
To simplify expressions involving fractional exponents, apply the rules of exponents:
- Product Rule: \(a^{m/n} \cdot a^{p/q} = a^{(mq+np)/nq}\)
- Quotient Rule: \(\frac{a^{m/n}}{a^{p/q}} = a^{(mq-np)/nq}\)
- Power Rule: \((a^{m/n})^p = a^{mp/n}\)
3. Examples of Simplification
- Simplify \(a^{\frac{3}{4}} \cdot a^{\frac{1}{4}}\):
- Using the product rule: \(a^{\frac{3}{4} + \frac{1}{4}} = a^{\frac{4}{4}} = a^1 = a\)
- Simplify \(\frac{a^{\frac{5}{6}}}{a^{\frac{1}{3}}}\):
- Using the quotient rule: \(a^{\frac{5}{6} - \frac{1}{3}} = a^{\frac{5}{6} - \frac{2}{6}} = a^{\frac{3}{6}} = a^{\frac{1}{2}} = \sqrt{a}\)
- Simplify \((a^{\frac{2}{5}})^3\):
- Using the power rule: \(a^{\frac{2 \cdot 3}{5}} = a^{\frac{6}{5}}\)
4. Converting Back to Radicals
To convert a fractional exponent back to a radical, use the reverse of the initial conversion:
\(a^{\frac{m}{n}} = \sqrt[n]{a^m} = (\sqrt[n]{a})^m\)
Examples:
- \(a^{\frac{3}{2}} = \sqrt{a^3} = (\sqrt{a})^3\)
- \(a^{\frac{5}{3}} = \sqrt[3]{a^5} = (\sqrt[3]{a})^5\)
By mastering the conversion between radicals and fractional exponents, and understanding the rules for simplifying these expressions, you can handle a wide variety of algebraic problems more efficiently.
Advanced Square Root Operations
Square root operations can extend beyond basic simplification and can be used in various advanced mathematical contexts. Here are some advanced techniques and operations involving square roots:
Addition and Subtraction of Square Roots
To add or subtract square roots, the radicands (the numbers under the square root) must be the same. If they are, you can add or subtract the coefficients (the numbers in front of the square root).
\( \sqrt{a} + \sqrt{a} = 2\sqrt{a} \)
\( \sqrt{a} - \sqrt{a} = 0 \)
If the radicands are different, you cannot directly add or subtract the square roots. However, sometimes you can simplify the radicals first to make them the same.
Multiplication of Square Roots
Multiplying square roots is straightforward: multiply the radicands and then take the square root of the product.
\( \sqrt{a} \times \sqrt{b} = \sqrt{a \times b} \)
For example:
\( \sqrt{2} \times \sqrt{8} = \sqrt{16} = 4 \)
Division of Square Roots
Similar to multiplication, you divide the radicands and then take the square root of the quotient.
\( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \)
For example:
\( \frac{\sqrt{18}}{\sqrt{2}} = \sqrt{\frac{18}{2}} = \sqrt{9} = 3 \)
Rationalizing the Denominator
Rationalizing the denominator involves rewriting a fraction so that the denominator is a rational number. This is done by multiplying the numerator and the denominator by a suitable radical that will eliminate the square root in the denominator.
For example:
\( \frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2} \)
Higher-Order Roots and Radical Expressions
Advanced square root operations also include handling higher-order roots, such as cube roots. The principles remain the same, but you work with cube roots or fourth roots instead of square roots.
For example, to simplify \( \sqrt[3]{54} \):
- Find a perfect cube factor: \( 54 = 27 \times 2 \)
- Rewrite the expression: \( \sqrt[3]{54} = \sqrt[3]{27 \times 2} = \sqrt[3]{27} \times \sqrt[3]{2} = 3\sqrt[3]{2} \)
Combining Radical Expressions
When dealing with expressions that combine different types of radicals, you can use the properties of exponents and roots to simplify them. For instance, combining square roots and fourth roots can involve finding a common root, such as the least common multiple of the roots.
For example:
\( \sqrt{a} \times \sqrt[4]{b} = \sqrt[4]{a^2 \times b} \)
By mastering these advanced square root operations, you can handle more complex mathematical problems and simplify expressions in various contexts.
Applications of Square Root Calculators
Square root calculators are invaluable tools for various applications in mathematics, science, engineering, and everyday problem-solving. Here are some key applications:
- Mathematical Problem Solving: Square root calculators help solve equations involving square roots, simplify radical expressions, and verify solutions. They are particularly useful in algebra, where finding the square root is often a step in solving quadratic equations.
- Geometry: In geometry, square root calculators are used to calculate the lengths of sides in right-angled triangles using the Pythagorean theorem, find the diagonal of rectangles, and solve other geometric problems involving distances and areas.
- Physics and Engineering: Square root calculations are essential in physics and engineering for solving problems related to wave propagation, electrical circuits, and material stress analysis. These fields often require precise square root calculations to determine root mean square (RMS) values, signal processing, and more.
- Statistics: In statistics, square root calculators are used to compute standard deviations and variances, which are crucial for data analysis and interpretation. These calculators help statisticians understand data distribution and variability.
- Financial Calculations: In finance, square root calculators assist in determining the volatility of stocks, calculating compound interest, and evaluating risk. They are used to compute the standard deviation of investment returns, which is a key measure of financial risk.
- Computer Science: Algorithms often require square root calculations for optimization and performance analysis. For example, they are used in search algorithms, graphics rendering, and machine learning models to normalize data and compute distances.
- Everyday Use: Square root calculators are handy for everyday problems such as resizing images, determining the correct dimensions for construction projects, and converting units. They help in finding the square footage of areas and volumes of objects, ensuring accuracy in practical applications.
Overall, square root calculators simplify complex calculations, making them accessible and manageable for students, professionals, and anyone needing precise square root computations in their daily activities.
Frequently Asked Questions
Here are some common questions about using a square root calculator in radical form:
-
What is a square root?
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9. The square root is denoted by the radical symbol (√).
-
How do I use a square root calculator?
To use a square root calculator, enter the number you wish to find the square root of into the input field and press the "Calculate" button. The calculator will display the square root of the given number.
-
Can I calculate square roots without a calculator?
Yes, square roots can be calculated manually using methods such as prime factorization or the long division method. However, a calculator simplifies the process and provides quick and accurate results.
-
Are there online tools for square root calculation?
Yes, there are many online tools and apps that can calculate square roots. Ensure you use a reliable source for accurate results.
-
What if I get an "error" message?
An error message may indicate an incorrect input or a limitation of the calculator. Double-check your input for any mistakes or consult the calculator's manual for troubleshooting tips.
-
How does the square root relate to other mathematical concepts?
The square root is foundational in many areas of mathematics, including algebra, geometry, and calculus. It is used to solve equations, understand geometric shapes, and explore advanced mathematical theories.
-
Can I find square roots of negative numbers?
The square root of a negative number is an imaginary number. For example, the square root of -1 is denoted as \(i\), where \(i\) is the imaginary unit. Calculators that handle complex numbers can calculate these roots.
-
What are perfect squares?
Perfect squares are numbers that are the squares of integers. For example, 1, 4, 9, 16, and 25 are perfect squares because they can be written as \(1^2\), \(2^2\), \(3^2\), \(4^2\), and \(5^2\) respectively.
-
How can I simplify square roots?
Square roots can be simplified by finding the prime factors of the number and pairing them. For instance, \( \sqrt{50} \) can be simplified to \( 5\sqrt{2} \) because \( 50 = 2 \times 5^2 \).

Additional Resources
For further learning and tools to assist with square root calculations and simplifications, you may find the following resources helpful:
- : This online calculator allows you to find the square root of any number and provides step-by-step explanations.
- : Offers a comprehensive tool for simplifying radicals and solving radical equations.
- : Simplifies square roots and provides detailed steps and explanations on how to perform these calculations.
- : A free tool that simplifies any square root to its simplest radical form and provides approximations for roots.
- : Offers a simple and easy-to-use calculator for finding the principal square root of any nonnegative number.
These resources are excellent for students, educators, and anyone looking to deepen their understanding of square roots and radical expressions. They offer practical tools and detailed explanations to help you master these concepts.
Simplifying square roots with a graphing calculator
ClassWiz Calculator Tutorial - Algebra 4-1 Simplifying Radicals
Simplifying Radicals
TI 84 Plus CE Simplifying Square Roots and Other Radicals
How to Convert a Decimal Into a Radical : Radical Numbers
Calculator Tutorial 9: Square roots on a scientific calculator
READ MORE: