Topic simplify square root of 200: Understanding how to simplify the square root of 200 can make complex math problems more manageable. In this article, we break down the process into simple steps, making it easy for anyone to grasp and apply. Whether you're a student or just love math, you'll find this guide helpful and engaging.
Table of Content
- Simplifying the Square Root of 200
- Introduction to Square Roots
- Understanding the Concept of Simplifying Square Roots
- Prime Factorization Method
- Steps to Simplify Square Root of 200
- Example Problems and Solutions
- Common Mistakes to Avoid
- Practice Exercises
- Applications in Real Life
- Conclusion and Key Takeaways
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai của 200. Khám phá các bước và kỹ thuật để tính toán một cách chính xác và dễ dàng.
Simplifying the Square Root of 200
The process of simplifying the square root of a number involves finding the prime factorization of the number and then simplifying the expression by grouping the prime factors into pairs.
Steps to Simplify √200
- Find the prime factorization of 200.
- Rewrite the square root using the prime factors.
- Simplify by grouping the prime factors into pairs.
Let's go through these steps in detail:
Step 1: Prime Factorization of 200
The prime factorization of 200 is:
\[ 200 = 2^3 \times 5^2 \]
Step 2: Rewrite the Square Root
Rewrite the square root of 200 using its prime factors:
\[ \sqrt{200} = \sqrt{2^3 \times 5^2} \]
Step 3: Simplify by Grouping
Group the prime factors into pairs:
\[ \sqrt{2^3 \times 5^2} = \sqrt{(2^2 \times 5^2) \times 2} \]
Take the square root of the pairs and simplify:
\[ \sqrt{(2^2 \times 5^2) \times 2} = 2 \times 5 \times \sqrt{2} \]
Therefore, the simplified form of √200 is:
\[ \sqrt{200} = 10\sqrt{2} \]
So, the simplified square root of 200 is \( 10\sqrt{2} \).

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is a fundamental concept in mathematics, particularly in algebra and geometry.
For example, the square root of 25 is 5, because \(5 \times 5 = 25\). The square root symbol is \( \sqrt{} \), and it is used to denote the square root of a number.
Key points to understand about square roots include:
- Every positive number has two square roots: a positive root and a negative root. For instance, the square roots of 16 are 4 and -4, because \(4 \times 4 = 16\) and \((-4) \times (-4) = 16\).
- The square root of 0 is 0.
- Negative numbers do not have real square roots because a real number squared always gives a non-negative result.
When simplifying square roots, the goal is to express the number in its simplest radical form. This often involves breaking down the number into its prime factors and pairing them to move them outside the radical sign.
For example, to simplify \(\sqrt{200}\), you would find the prime factors of 200, which are \(2^3 \times 5^2\), and then simplify to get \(10\sqrt{2}\). This process helps in solving equations more easily and understanding the properties of numbers more deeply.
Square roots are used in various applications, from solving quadratic equations to determining distances in geometry. Mastering this concept is essential for progressing in higher levels of math.
Understanding the Concept of Simplifying Square Roots
Simplifying square roots involves expressing a square root in its simplest form. This process can make mathematical expressions easier to work with and understand.
To simplify a square root, follow these steps:
- Identify the Prime Factors: Break down the number inside the square root into its prime factors. For example, for 200, the prime factorization is \(2^3 \times 5^2\).
- Group the Factors: Pair the prime factors into groups of two. Each pair of the same number can be moved outside the square root. For 200, we have:
- \(2^3\) can be written as \(2^2 \times 2\)
- \(5^2\) is already a pair
- Simplify the Expression: Move each pair of prime factors outside the square root, and multiply them together. Leave any unpaired factors inside the square root. For 200, this gives us:
\[ \sqrt{200} = \sqrt{2^2 \times 5^2 \times 2} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2} \]
Through these steps, we see that \(\sqrt{200}\) simplifies to \(10\sqrt{2}\). This means that the original square root has been expressed in a simpler, more manageable form.
By understanding and applying the concept of simplifying square roots, you can solve mathematical problems more efficiently and develop a deeper comprehension of number properties.
Prime Factorization Method
The prime factorization method is a systematic way to simplify square roots by breaking down a number into its prime factors and then pairing them. This method makes it easier to find the square root of a number, especially if it is not a perfect square.
To simplify the square root of 200 using the prime factorization method, follow these steps:
- First, find the prime factors of 200.
- 200 can be divided by 2 (the smallest prime number):
- 200 ÷ 2 = 100
- 100 ÷ 2 = 50
- 50 ÷ 2 = 25
- 25 is not divisible by 2, so we move to the next prime number, which is 5:
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
- Write 200 as a product of its prime factors:
- 200 = 2 × 2 × 2 × 5 × 5
- This can also be written as: 200 = 23 × 52
- Pair the prime factors:
- Group the pairs of prime factors: (2 × 2) and (5 × 5)
- We have one 2 left unpaired: 200 = (2 × 2) × (5 × 5) × 2
- Take one number from each pair outside the square root:
- √200 = √((2 × 2) × (5 × 5) × 2)
- √200 = 2 × 5 × √2
- √200 = 10√2
Thus, the simplified form of √200 is 10√2.
Here's a table for a quick reference of the steps:
| Step | Description | Result |
|---|---|---|
| 1 | Prime Factorization | 200 = 2 × 2 × 2 × 5 × 5 |
| 2 | Write as Exponents | 200 = 23 × 52 |
| 3 | Pair the Factors | (2 × 2) and (5 × 5), with one 2 left |
| 4 | Simplify | 10√2 |
By following these steps, you can simplify the square root of any number using the prime factorization method.
Steps to Simplify Square Root of 200
The process of simplifying the square root of 200 involves a few straightforward steps using prime factorization. Here's a detailed, step-by-step guide:
-
Prime Factorization: Begin by finding the prime factors of 200. The number 200 can be broken down as follows:
\( 200 = 2 \times 100 \)
\( 100 = 2 \times 50 \)
\( 50 = 2 \times 25 \)
\( 25 = 5 \times 5 \)
Thus, the prime factorization of 200 is:
\( 200 = 2 \times 2 \times 2 \times 5 \times 5 \) or \( 200 = 2^3 \times 5^2 \)
-
Group the Factors: Group the prime factors into pairs of the same number under the radical:
\( \sqrt{200} = \sqrt{2^3 \times 5^2} \)
This can be expressed as:
\( \sqrt{200} = \sqrt{(2^2 \times 5^2) \times 2} \)
-
Simplify Inside the Radical: Take one factor from each pair outside the radical:
\( \sqrt{200} = \sqrt{(2^2) \times (5^2) \times 2} \)
\( \sqrt{200} = \sqrt{2^2} \times \sqrt{5^2} \times \sqrt{2} \)
\( \sqrt{200} = 2 \times 5 \times \sqrt{2} \)
-
Combine the Factors: Multiply the numbers outside the radical:
\( \sqrt{200} = 10 \sqrt{2} \)
-
Result: Therefore, the simplified form of the square root of 200 is:
\( \sqrt{200} = 10 \sqrt{2} \)
Using this method, you can simplify the square root of any number by breaking it down into its prime factors and then simplifying the radical expression step by step.
Example Problems and Solutions
In this section, we will work through some example problems to solidify our understanding of simplifying square roots, specifically the square root of 200.
Example 1: Simplifying Square Root of 200
Let's simplify \(\sqrt{200}\) using the prime factorization method.
- First, find the prime factorization of 200:
- \(200 = 2 \times 2 \times 2 \times 5 \times 5\)
- Next, pair the prime factors:
- \(200 = (2 \times 2) \times (5 \times 5) \times 2\)
- Take one number from each pair outside the square root:
- \(\sqrt{200} = \sqrt{(2 \times 2) \times (5 \times 5) \times 2} = 2 \times 5 \times \sqrt{2}\)
- Simplify the expression:
- \(\sqrt{200} = 10\sqrt{2}\)
Example 2: Simplifying 25 + \(\sqrt{200}\)
Given the expression \(25 + \sqrt{200}\), simplify it.
- We know from the previous example that \(\sqrt{200} = 10\sqrt{2}\).
- Substitute this value into the expression:
- \(25 + \sqrt{200} = 25 + 10\sqrt{2}\)
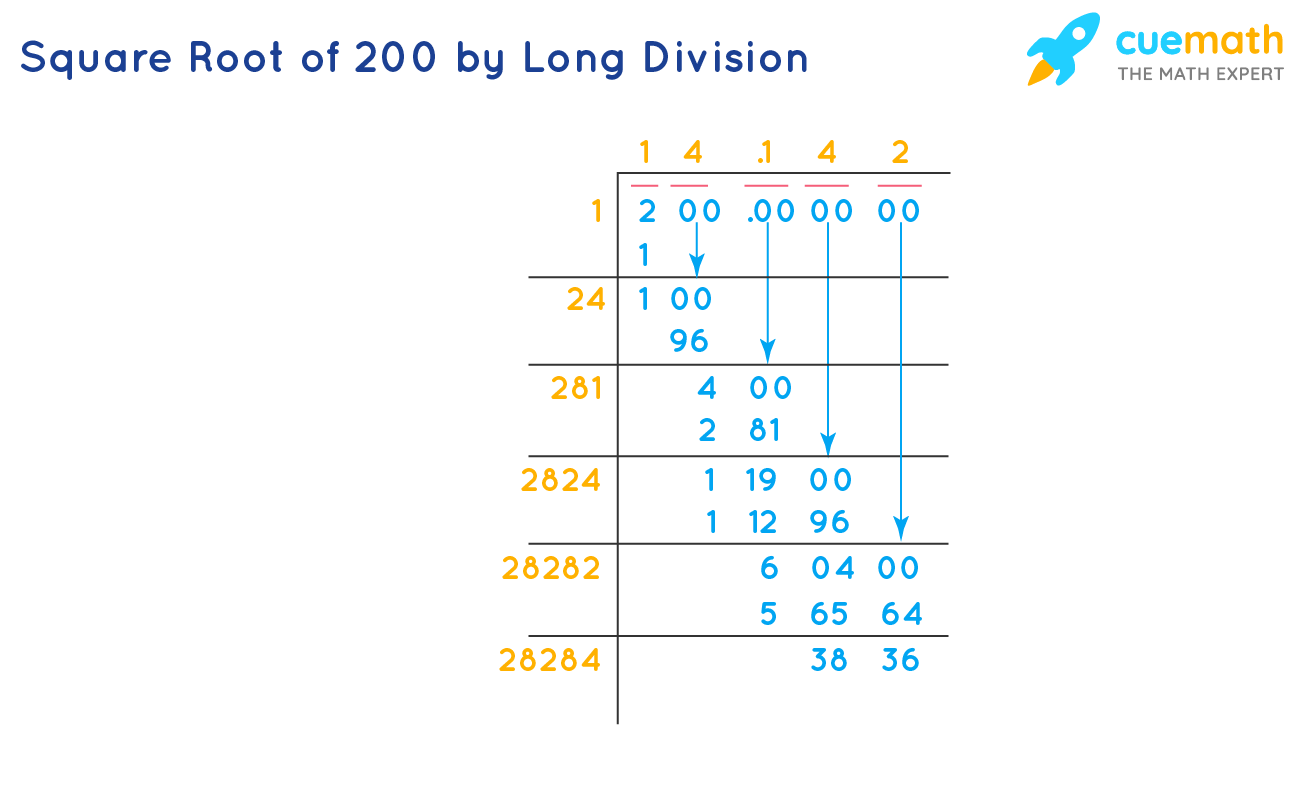
Example 3: Solving for \(m\) in \(\sqrt{200m} = 28.284\)
Solve for \(m\) if \(\sqrt{200m} = 28.284\).
- We know that \(\sqrt{200} = 14.142\).
- Set up the equation:
- \(\sqrt{200m} = 28.284\)
- Square both sides to eliminate the square root:
- \(200m = 28.284^2\)
- Calculate the square of 28.284:
- \(28.284^2 = 800\)
- Solve for \(m\):
- \(200m = 800\)
- \(m = \frac{800}{200} = 4\)
Example 4: Simplifying \((5\sqrt{200} \times 10\sqrt{2}) + 12\)
Simplify the expression \((5\sqrt{200} \times 10\sqrt{2}) + 12\).
- We know that \(\sqrt{200} = 10\sqrt{2}\).
- Substitute this value into the expression:
- \(5\sqrt{200} = 5 \times 10\sqrt{2} = 50\sqrt{2}\)
- Multiply the simplified terms:
- \(50\sqrt{2} \times 10\sqrt{2} = 50 \times 10 \times (\sqrt{2} \times \sqrt{2})\)
- \(50 \times 10 \times 2 = 1000\)
- Add the constant term:
- \(1000 + 12 = 1012\)
Common Mistakes to Avoid
Simplifying square roots can sometimes lead to common mistakes that students frequently encounter. Here are some of the most common errors and how to avoid them:
- Forgetting to Check for Perfect Squares: Always ensure to check if the number under the square root is a perfect square before attempting any other simplification. For example, failing to recognize that \(\sqrt{100}\) simplifies directly to 10 can lead to unnecessary steps.
- Incorrect Prime Factorization: Ensure that the prime factorization of the number is done correctly. Mistakes in factorizing can lead to incorrect simplification of the square root. For example, factorizing 200 correctly as \(2^3 \times 5^2\) is crucial.
- Rushing Through the Simplification Process: Simplifying square roots requires careful step-by-step work. Rushing through the process can lead to mistakes. Take your time to write down each step clearly.
- Ignoring the Need to Simplify Completely: Sometimes, students stop the simplification process too early. Make sure to simplify the square root as much as possible. For example, \(\sqrt{72}\) should be simplified to \(6\sqrt{2}\), not left as \(\sqrt{36 \times 2}\).
- Misinterpreting the Properties of Square Roots: Remember that \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) and not \(\sqrt{a} + \sqrt{b}\). Mixing these properties can lead to incorrect results.
- Not Considering Both Positive and Negative Roots: When solving equations involving square roots, remember that both positive and negative roots should be considered. For example, solving \(x^2 = 9\) gives \(x = 3\) and \(x = -3\).
- Improper Use of the Equals Sign: Ensure that each step of the simplification maintains the balance of the equation. Misuse of the equals sign can lead to incorrect solutions.
- Neglecting to Rationalize the Denominator: When a square root appears in the denominator, it should be rationalized. For example, \(\frac{1}{\sqrt{2}}\) should be simplified to \(\frac{\sqrt{2}}{2}\).
Avoiding these common mistakes will help ensure that your simplification of square roots is accurate and effective. Practice regularly and take your time with each problem to build confidence and proficiency.
Practice Exercises
Here are some practice exercises to help you master simplifying square roots:
- Simplify \(\sqrt{50}\).
- Simplify \(\sqrt{72}\).
- Simplify \(\sqrt{128}\).
- Simplify \(\sqrt{180}\).
- Simplify \(\sqrt{225}\).
For more advanced practice, try simplifying expressions involving variables:
- Simplify \(\sqrt{x^2}\).
- Simplify \(\sqrt{49y^2}\).
- Simplify \(\sqrt{144z^4}\).
- Simplify \(\sqrt{25a^{10}}\).
- Simplify \(\sqrt{36b^{6}}\).
Finally, test your skills with these mixed problems:
- Simplify \(\sqrt{9} + \sqrt{16}\).
- Simplify \(\sqrt{4 \cdot 25}\).
- Simplify \(\sqrt{100} \cdot \sqrt{4}\).
- Simplify \(\sqrt{49x^2} + \sqrt{64}\).
- Simplify \(\sqrt{16y^4} - \sqrt{81}\).
Make sure to work through these exercises step-by-step, breaking down each problem into its prime factors before simplifying. Practice makes perfect!
Applications in Real Life
Simplifying square roots has various practical applications in real life. Understanding these applications can make the concept more relatable and highlight its importance. Here are a few key areas where simplified square roots are commonly used:
1. Architecture and Construction
In architecture and construction, precise measurements are crucial. For instance, if you know the area of a square space, you can find the length of its sides by taking the square root of the area. For example:
- Problem: If a square patio has an area of 200 square feet, what is the length of each side?
- Solution: The length of each side is \(\sqrt{200}\), which simplifies to approximately 14.1 feet.
2. Physics and Engineering
Simplified square roots are often used in physics and engineering to solve problems related to motion, forces, and energy. For example:
- Problem: If an object is dropped from a height of 400 feet, how long will it take to reach the ground?
- Solution: The time \( t \) in seconds is given by the formula \( t = \frac{\sqrt{h}}{4} \). Substituting \( h = 400 \) gives \( t = \frac{\sqrt{400}}{4} = 5 \) seconds.
3. Accident Investigations
Police officers use square roots to determine the speed of a car before it braked, based on the length of the skid marks. For example:
- Problem: A car leaves skid marks measuring 190 feet. What was the speed of the car before braking?
- Solution: The speed \( v \) in mph can be found using the formula \( v = \sqrt{24d} \), where \( d \) is the length of the skid marks. Substituting \( d = 190 \) gives \( v = \sqrt{24 \times 190} \approx 67.5 \) mph.
4. Everyday Problem Solving
Square roots are also useful in everyday problem-solving situations, such as determining the dimensions of a room, estimating distances, or calculating material requirements.
Overall, understanding how to simplify square roots and apply them in real life can make mathematical concepts more tangible and useful, highlighting their importance beyond the classroom.

Conclusion and Key Takeaways
Simplifying square roots is a valuable mathematical skill that can be applied in various contexts. By understanding and mastering the methods for simplifying square roots, such as prime factorization and the use of perfect squares, you can make complex calculations more manageable.
Here are the key takeaways from our discussion on simplifying the square root of 200:
- Prime Factorization Method: Breaking down the number into its prime factors helps in identifying perfect square factors, making the simplification process straightforward.
- Perfect Square Factors: Recognizing perfect squares within a number allows you to simplify the square root by extracting these factors. For example, 200 can be expressed as \( 100 \times 2 \), leading to \( \sqrt{200} = 10\sqrt{2} \).
- Application of the Product Rule for Radicals: This rule helps in simplifying expressions by separating the square root of a product into the product of square roots.
- Common Mistakes to Avoid: Ensuring correct factorization and proper application of rules is essential to avoid errors in simplification.
- Practice and Application: Regular practice with varied examples and exercises solidifies understanding and helps in applying these concepts effectively in real-life scenarios, such as geometry and physics problems.
By consistently practicing these techniques, you will develop a strong foundation in simplifying square roots, enhancing your overall mathematical proficiency. Remember, the key is to break down the problem into manageable parts and apply the rules methodically.
Happy simplifying!
Video hướng dẫn cách đơn giản hóa căn bậc hai của 200. Khám phá các bước và kỹ thuật để tính toán một cách chính xác và dễ dàng.
sqrt(200), căn bậc hai của 200 đơn giản hóa
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai của 200. Khám phá các bước và phương pháp để tính toán một cách chính xác và dễ dàng.
Đơn giản hóa căn bậc hai của 200







