Topic 4 square root calculator: Unlock the full potential of the 4 Square Root Calculator with our ultimate guide. Learn the ins and outs of calculating square roots, simplify your math problems, and master complex calculations with ease. Perfect for students, educators, and math enthusiasts looking to enhance their mathematical skills.
Table of Content
- Square Root Calculator
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- How to Use a Square Root Calculator
- Step-by-Step Instructions
- Examples of Calculations
- Simplifying Square Roots
- Square Roots of Perfect Squares
- Dealing with Non-Perfect Squares
- Complex and Imaginary Square Roots
- Applications of Square Roots
- Common Problems and Solutions
- Advanced Topics in Square Roots
- Conclusion
- YOUTUBE:
Square Root Calculator
Here's a summary of the search results for a 4 square root calculator:
- Calculator.net provides a simple interface to calculate the square root of 4, displaying the result as 2.
- RapidTables offers a tool where entering 4 yields a square root of 2, also showing the result in decimal form.
- MathPortal.org features a square root calculator that confirms the square root of 4 is 2.
- OnlineCalculator.guru calculates the square root of 4 as 2 with a clear step-by-step explanation.
These calculators demonstrate that the square root of 4 is consistently calculated as 2 across different platforms.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol “√”. For example, the square root of 9 is 3, because 3 × 3 = 9. Square roots are essential in various areas of mathematics and practical applications.
Here are some key points to understand about square roots:
- Principal Square Root: This is the nonnegative square root of a number. For example, the principal square root of 25 is 5, denoted as √25 = 5.
- Perfect Squares: These are numbers whose square roots are integers. Examples include 1, 4, 9, 16, 25, etc.
- Non-Perfect Squares: These are numbers whose square roots are not integers, often resulting in an irrational number. For example, √2 is approximately 1.414, and it is an irrational number.
Using a square root calculator simplifies the process of finding square roots, especially for non-perfect squares. A typical square root calculator requires you to:
- Enter the number you want to find the square root of in the designated input field.
- Click the "Calculate" button to get the result.
- View the square root result, which is displayed in both exact form (if applicable) and decimal form.
Understanding square roots is crucial for solving quadratic equations, working with geometric shapes, and performing various mathematical operations.
Understanding the Concept of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square roots of 9 are 3 and -3 because 3 × 3 = 9 and (-3) × (-3) = 9. Every positive number has two square roots: one positive (principal square root) and one negative.
To denote the principal square root, we use the radical symbol (√). For instance, the square root of 16 is written as √16, which equals 4. The principal square root is the non-negative root and is typically the one referred to in most contexts.
Properties of Square Roots
- For any positive real number \( a \), \( \sqrt{a^2} = a \) and \( (\sqrt{a})^2 = a \).
- For any numbers \( a \) and \( b \), \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \) and \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- The square root of a fraction \( \frac{a}{b} \) is \( \frac{\sqrt{a}}{\sqrt{b}} \).
Examples of Calculations
Let's explore some examples:
- \(\sqrt{25} = 5\) because \(5 \times 5 = 25\).
- \(\sqrt{49} = 7\) because \(7 \times 7 = 49\).
- \(\sqrt{0.25} = 0.5\) because \(0.5 \times 0.5 = 0.25\).
Square Roots of Negative Numbers
Square roots of negative numbers are not real numbers because no real number squared gives a negative result. However, in the context of complex numbers, the square root of a negative number involves the imaginary unit \( i \), where \( i = \sqrt{-1} \). For example, \( \sqrt{-4} = 2i \).
Applications of Square Roots
Square roots are used in various fields of mathematics and science, including solving quadratic equations, calculating areas and volumes in geometry, and analyzing scientific data. Understanding square roots is fundamental to many areas of study and practical applications.
How to Use a Square Root Calculator
Using a square root calculator is straightforward and can be a great help in solving mathematical problems involving square roots. Here is a step-by-step guide on how to use a square root calculator effectively:
-
Input the Number:
Enter the number for which you want to find the square root into the calculator. This number can be a positive number or, in some advanced calculators, a negative number.
-
Select the Calculation:
Choose the square root function on the calculator. This is usually represented by the radical symbol (√). Some calculators might require you to press a specific button to activate the square root function.
-
Calculate:
Press the "Calculate" or "Enter" button to get the result. The calculator will display the principal square root of the number. For example, the square root of 16 will be shown as 4.
-
Interpret the Result:
Understand the result provided by the calculator. If the input number is a perfect square, the result will be an integer. For example, √25 = 5. If the input number is not a perfect square, the result will be a decimal. For example, √10 ≈ 3.16228.
-
Check for Negative Numbers:
If you input a negative number, some calculators will provide an error, while others will give the imaginary result. For example, √-4 = 2i, where 'i' is the imaginary unit.
Using these steps, you can easily find the square root of any number using a square root calculator, making your calculations quicker and more accurate.
Step-by-Step Instructions
Using a square root calculator can simplify the process of finding the square root of any number. Follow these detailed steps to use a square root calculator effectively:
- Access the Calculator:
Open the square root calculator on your preferred device. Ensure you have a stable internet connection if you're using an online calculator.
- Enter the Number:
Input the number for which you want to find the square root into the calculator's input field. This number is called the radicand.
- Initiate the Calculation:
Click the button labeled "Calculate" or "Find Square Root" to start the calculation process. The calculator will process your input and display the square root.
- Review the Result:
The square root of the entered number will be displayed. For example, if you entered 16, the calculator will show 4, because \(\sqrt{16} = 4\).
- Use the Result:
You can now use this result for your mathematical computations or problem-solving tasks.
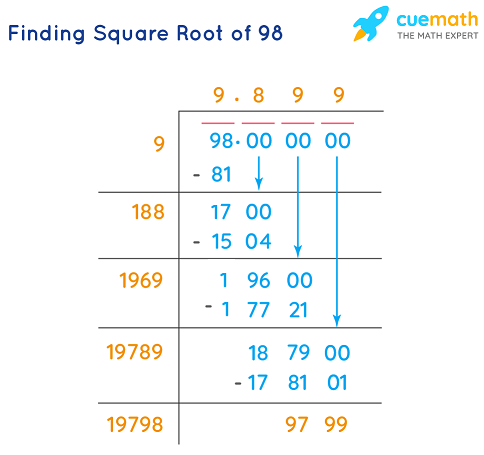
In addition to finding the square root of a number, some advanced calculators provide step-by-step solutions, including:
- Separation of Digits:
For example, separating the number 5836.36 into 58 and 36.36 for easier computation.
- Finding the Nearest Perfect Square:
Identifying the closest perfect square to each segment of the number.
- Subtraction and Carry-Over:
Subtracting and carrying over digits as you continue to compute the square root.
- Iteration:
Repeating the steps until the desired precision is achieved.
Using these steps, you can manually compute the square root of any number, which can be especially useful for understanding the underlying process.
Examples of Calculations
Using a square root calculator can make the process of finding square roots much easier. Below are some examples to illustrate how to use the calculator for various calculations:
Example 1: Square Root of a Perfect Square
To find the square root of a perfect square such as 64, you can simply input the number into the calculator and get the result:
- Input:
64 - Output:
\(\sqrt{64} = 8\)
Example 2: Square Root of a Non-Perfect Square
For non-perfect squares, the calculator provides a decimal approximation:
- Input:
50 - Output:
\(\sqrt{50} \approx 7.071\)
Example 3: Simplifying a Square Root
The calculator can also help simplify square roots by factoring out perfect squares:
- Input:
72 - Simplification Steps:
- Factor 72:
72 = 36 \times 2 - Simplify:
\(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\)
- Factor 72:
- Output:
\(6\sqrt{2}\)
Example 4: Complex Square Root
The calculator can handle complex numbers as well:
- Input:
-25 - Output:
\(\sqrt{-25} = 5i\)
Example 5: Square Root of a Fraction
You can find the square root of a fraction by applying the square root to both the numerator and the denominator:
- Input:
\(\frac{9}{16}\) - Output:
\(\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}\)
Example 6: Using the Property of Square Roots
Using properties such as \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\), you can simplify calculations:
- Input:
45 - Simplification Steps:
- Factor 45:
45 = 9 \times 5 - Simplify:
\(\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}\)
- Factor 45:
- Output:
\(3\sqrt{5}\)
These examples demonstrate how versatile and powerful a square root calculator can be for solving a wide range of problems involving square roots.
Simplifying Square Roots
Simplifying square roots involves expressing the square root of a number in its simplest form. This often requires identifying factors of the number that are perfect squares. Here is a detailed step-by-step guide to simplify square roots:
- Identify the factors of the number under the square root (radicand).
- Look for the largest perfect square factor of the radicand.
- Use the property
\(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) to separate the perfect square from the other factor. - Simplify the square root of the perfect square.
- Combine the simplified square root with the remaining square root factor.
Let's look at some examples to understand the process:
- Simplifying √72:
- Identify factors: 72 = 36 × 2
- Largest perfect square factor: 36
- Apply the property:
\(\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2}\) - Simplify the perfect square:
\(\sqrt{36} = 6\) - Combine the results:
\(\sqrt{72} = 6\sqrt{2}\) - Simplifying √50:
- Identify factors: 50 = 25 × 2
- Largest perfect square factor: 25
- Apply the property:
\(\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2}\) - Simplify the perfect square:
\(\sqrt{25} = 5\) - Combine the results:
\(\sqrt{50} = 5\sqrt{2}\) - Simplifying √18:
- Identify factors: 18 = 9 × 2
- Largest perfect square factor: 9
- Apply the property:
\(\sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt{2}\) - Simplify the perfect square:
\(\sqrt{9} = 3\) - Combine the results:
\(\sqrt{18} = 3\sqrt{2}\)
By following these steps, you can simplify most square roots efficiently. Practice with different numbers to become more comfortable with the process.
Square Roots of Perfect Squares
Perfect squares are numbers that are the square of an integer. For example, 1, 4, 9, 16, 25, and so on, are all perfect squares. The square root of a perfect square is always an integer. Here are some examples to illustrate:
- The square root of \(1\) is \( \sqrt{1} = 1 \).
- The square root of \(4\) is \( \sqrt{4} = 2 \).
- The square root of \(9\) is \( \sqrt{9} = 3 \).
- The square root of \(16\) is \( \sqrt{16} = 4 \).
- The square root of \(25\) is \( \sqrt{25} = 5 \).
- The square root of \(36\) is \( \sqrt{36} = 6 \).
- The square root of \(49\) is \( \sqrt{49} = 7 \).
- The square root of \(64\) is \( \sqrt{64} = 8 \).
- The square root of \(81\) is \( \sqrt{81} = 9 \).
- The square root of \(100\) is \( \sqrt{100} = 10 \).
Notice how each of these perfect squares results in an integer when their square roots are calculated. This makes perfect squares easy to work with and recognize. Here's a more structured look at perfect squares up to \(12\):
| Number | Square |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
To further understand perfect squares, let's consider some properties:
- A perfect square always ends in 0, 1, 4, 5, 6, or 9 in base 10.
- The square root of a perfect square is always a whole number.
Knowing the perfect squares can greatly simplify solving square root problems, especially when using a calculator or when doing mental math.
Dealing with Non-Perfect Squares
Non-perfect squares are numbers that do not have an integer as their square root. Calculating the square root of such numbers involves approximations or simplifications to their simplest radical form. Here’s a step-by-step guide on how to deal with non-perfect squares:
1. Simplifying the Square Root
To simplify the square root of a non-perfect square, follow these steps:
- Identify the prime factors of the number under the square root.
- Pair the prime factors in groups of two.
- Move one factor from each pair outside the square root.
- Multiply the factors outside the square root.
- If there are any unpaired factors, leave them inside the square root.
For example, to simplify :
- Prime factorization of 50: 50 = 2 × 5 × 5
- Pair the 5s: 50 = (5 × 5) × 2
- Move one 5 outside the square root:
2. Approximating the Square Root
For a decimal approximation of a non-perfect square root, use a calculator or follow these steps manually:
- Make an initial guess for the square root.
- Divide the number by your guess.
- Averaging the result with your guess gives a new guess.
- Repeat steps 2 and 3 until the guess is accurate enough.
For example, to approximate :
- Initial guess: 5
- Divide: 30 / 5 = 6
- Average: (5 + 6) / 2 = 5.5
- Repeat: 30 / 5.5 ≈ 5.454, (5.5 + 5.454) / 2 ≈ 5.477
So, .
3. Example Calculations
Here are a few more examples of dealing with non-perfect squares:
- : Prime factors are 2 × 3 × 3, so
- : Prime factors are 3 × 3 × 5, so
By following these methods, you can effectively handle and simplify square roots of non-perfect squares.

Complex and Imaginary Square Roots
When dealing with square roots of negative numbers, we enter the realm of complex and imaginary numbers. The square root of a negative number is not a real number but an imaginary number. The concept of imaginary numbers is based on the imaginary unit \( i \), where \( i \) is defined as \( \sqrt{-1} \).
Here are the steps to find the square root of a negative number:
- Identify the negative number for which you want to find the square root. For example, let's take \(-25\).
- Separate the negative sign from the number and express it in terms of \( i \). For instance, \(\sqrt{-25} = \sqrt{25 \cdot (-1)} = \sqrt{25} \cdot \sqrt{-1}\).
- Simplify the square root of the positive number and multiply it by \( i \). In our example, \(\sqrt{25} = 5\), so \(\sqrt{-25} = 5i\).
Here's another example with a negative number:
- \(\sqrt{-64}\)
- \(\sqrt{-64} = \sqrt{64 \cdot (-1)} = \sqrt{64} \cdot \sqrt{-1}\)
- \(\sqrt{64} = 8\), so \(\sqrt{-64} = 8i\)
Imaginary numbers are a part of complex numbers, which have both a real part and an imaginary part. A complex number is generally represented as \( a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit.
For instance:
| Expression | Simplified Form |
|---|---|
| \(\sqrt{-1}\) | \(i\) |
| \(\sqrt{-4}\) | \(2i\) |
| \(\sqrt{-9}\) | \(3i\) |
| \(\sqrt{-16}\) | \(4i\) |
By understanding and using the imaginary unit \( i \), we can simplify the square roots of negative numbers and work with complex numbers in various mathematical and engineering fields.
Applications of Square Roots
Square roots have a wide range of applications in various fields, from mathematics and physics to engineering and finance. Understanding these applications can help you appreciate the importance of mastering square root calculations.
- Mathematics:
- Solving Quadratic Equations: Square roots are essential in solving quadratic equations of the form \( ax^2 + bx + c = 0 \) using the quadratic formula: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
- Geometry: Square roots are used to calculate distances between points in coordinate geometry, as well as in determining the side lengths of right triangles using the Pythagorean theorem: \[ c = \sqrt{a^2 + b^2} \]
- Physics:
- Wave Mechanics: The square root function is used in the equations describing wave speed and intensity. For example, the speed of a wave on a string is given by: \[ v = \sqrt{\frac{T}{\mu}} \] where \( T \) is the tension in the string and \( \mu \) is the mass per unit length.
- Relativity: In special relativity, the Lorentz factor involves square roots: \[ \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \] where \( v \) is the velocity of the object and \( c \) is the speed of light.
- Engineering:
- Signal Processing: Square roots are used in algorithms for processing signals, including calculating root mean square (RMS) values of signals, which represent their effective power.
- Structural Analysis: Engineers use square roots to determine stresses and strains in materials, which involve calculations using the square root of the sum of squares of forces and moments.
- Finance:
- Risk Assessment: In finance, the standard deviation, which measures the volatility of an investment, is calculated using the square root of the variance: \[ \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2} \] where \( N \) is the number of observations, \( x_i \) are the data points, and \( \mu \) is the mean.
- Compound Interest: Square roots can be used in compound interest formulas, particularly when dealing with continuous compounding and finding effective interest rates.
Understanding these applications can enhance your ability to use square roots effectively in various practical scenarios.
Common Problems and Solutions
Using a 4 square root calculator can sometimes present challenges. Here are some common problems users might encounter and their solutions:
Problem 1: Incorrect Input Format
One of the most frequent issues is entering the number in an incorrect format. Ensure the number is entered correctly to get accurate results.
- Solution: Check the format of your input. The calculator typically requires a numerical input without any additional characters or spaces.
Problem 2: Complex or Imaginary Results
When dealing with negative numbers, the calculator might return complex or imaginary numbers, which can be confusing for some users.
- Solution: Understand that the square root of a negative number involves imaginary numbers. For example, the square root of -16 is \(4i\), where \(i\) is the imaginary unit.
Example:
Input: \(\sqrt{-16}\)
Output: \(4i\)
Problem 3: Large Numbers
Calculating the square root of very large numbers can be challenging and may result in very large or very small decimal numbers.
- Solution: Use the calculator's precision settings to manage large numbers. If the result is too complex, consider using scientific notation.
Example:
Input: \(\sqrt{123456789}\)
Output: \(11111.11106\)
Problem 4: Simplifying Square Roots
Users may struggle with simplifying square roots into their simplest radical form.
- Solution: Factorize the number under the square root to its prime factors and then simplify.
Example:
Input: \(\sqrt{72}\)
Steps: \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\)
Problem 5: Rounding Errors
Rounding errors can occur when the calculator provides a result to a limited number of decimal places.
- Solution: Check the number of decimal places your calculator is set to display. Adjust the settings to ensure the accuracy you need.
Example:
Input: \(\sqrt{50}\)
Output: \(7.071\) (rounded to three decimal places)
Problem 6: Misinterpretation of Results
Users may misinterpret the results, especially when dealing with approximate values.
- Solution: Always double-check your results and understand the context in which you're using the square root. If necessary, consult additional resources or perform manual calculations to verify.
Example:
Input: \(\sqrt{20}\)
Output: \(4.472\), but note that \(\sqrt{20} \approx 4.472\)
By addressing these common problems, users can effectively use a 4 square root calculator and achieve accurate results.
Advanced Topics in Square Roots
Understanding advanced topics in square roots requires a deeper dive into mathematical concepts beyond basic calculations. Here, we explore some of these topics in detail.
1. Square Roots of Complex Numbers
While square roots of positive real numbers are straightforward, finding the square roots of negative numbers introduces us to complex numbers. A complex number is of the form \(a + bi\), where \(i\) is the imaginary unit with the property that \(i^2 = -1\). The square root of a negative number can be expressed as:
\[\sqrt{-x} = \sqrt{x} \cdot i\]
For example:
\[\sqrt{-16} = \sqrt{16} \cdot i = 4i\]
2. Higher Order Roots
Square roots are a specific case of nth roots. The cube root of a number \(x\), denoted as \(\sqrt[3]{x}\), is a number \(a\) such that \(a^3 = x\). Higher order roots can be calculated similarly to square roots but require identifying factors that are perfect cubes:
- Example: \(\sqrt[3]{27} = 3\) because \(3^3 = 27\).
- Example: \(\sqrt[3]{64} = 4\) because \(4^3 = 64\).
3. Fractional Exponents and Roots
Fractional exponents provide an alternative way to represent roots. The nth root of \(x\) can be written as \(x^{1/n}\). For square roots, this is represented as \(x^{1/2}\):
\[ \sqrt{x} = x^{1/2} \]
This notation is particularly useful in algebra and calculus when manipulating expressions involving roots.
4. Simplifying Radical Expressions
To simplify radical expressions, use properties of radicals to combine and reduce terms:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\)
For example, to simplify \(\sqrt{50}\):
\[\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\]
5. Rationalizing the Denominator
Rationalizing the denominator involves rewriting expressions to eliminate radicals from the denominator:
Example: \(\frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
6. Applications of Square Roots
Square roots have various applications in different fields such as physics, engineering, and statistics. For instance:
- Calculating standard deviation in statistics.
- Solving quadratic equations in algebra.
- Determining distances in geometry using the Pythagorean theorem.
7. Square Roots in Calculus
In calculus, square roots are often encountered in limits, derivatives, and integrals. For example, the derivative of \(f(x) = \sqrt{x}\) is found using the chain rule:
\[ f'(x) = \frac{1}{2}x^{-1/2} = \frac{1}{2\sqrt{x}} \]

Conclusion
In conclusion, using a 4 square root calculator can greatly simplify the process of finding the square roots of both perfect and non-perfect squares. By leveraging the advanced capabilities of such calculators, you can ensure accurate and quick calculations, whether you are dealing with simple square roots or more complex expressions.
Throughout this guide, we have covered various aspects of square roots, including understanding the basic concept, using a calculator effectively, simplifying square roots, and tackling common problems. We also explored advanced topics such as the application of square roots in different fields and the handling of complex and imaginary square roots.
Here are some key takeaways:
- Square roots represent the value that, when multiplied by itself, gives the original number.
- Square root calculators are valuable tools for students, educators, and professionals dealing with mathematical problems.
- Simplifying square roots involves breaking down the number under the radical into its prime factors.
- Advanced calculators can handle complex numbers and provide results in both exact and decimal forms.
- Understanding and applying the properties of square roots can simplify many mathematical problems.
By incorporating these insights and techniques into your mathematical toolkit, you can approach square root calculations with confidence and ease. Whether for academic purposes, professional applications, or personal curiosity, mastering the use of a 4 square root calculator will enhance your mathematical skills and efficiency.
Thank you for exploring this comprehensive guide. We hope it has provided you with valuable knowledge and practical strategies for using square root calculators effectively.
Cách Làm Căn Bậc 4 và Căn Bậc 5 Trên Máy Tính Casio (Các Căn Bậc Cao Hơn)
READ MORE:
Cách sử dụng máy tính fx-570ms để tính căn bậc hai của 4?