Simplify the Square Root Calculator: Your Ultimate Guide to Mastering Square Root Simplification

The process of simplifying a square root involves finding the prime factors of the number inside the square root and then applying the rule \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).

Steps to Simplify a Square Root

1. Factorize the number inside the square root into its prime factors.
2. Pair the prime factors in groups of two.
3. Move each pair of prime factors outside the square root as a single number.
4. Multiply the numbers outside the square root together.
5. If there are any prime factors left inside the square root, multiply them together and keep them under the square root.

Example: Simplify \( \sqrt{72} \)

Let's simplify \( \sqrt{72} \) step-by-step:

1. Factorize 72 into its prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
2. Group the prime factors into pairs: \( (2 \times 2), (3 \times 3), 2 \).
3. Move the pairs outside the square root: \( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} \).
4. Multiply the numbers outside the square root: \( 2 \times 3 = 6 \).
5. The simplified form is \( 6 \sqrt{2} \).

Key Points to Remember

• Only pairs of prime factors can be moved outside the square root.
• The simplified form should have no pairs of prime factors left inside the square root.
• Simplifying square roots makes them easier to handle in further calculations.

Useful Calculator for Simplifying Square Roots

To simplify square roots quickly and accurately, you can use online calculators that perform these steps automatically. Simply enter the number, and the calculator will provide the simplified form.

Practice Problems

Try simplifying the following square roots:

1. \( \sqrt{50} \)
2. \( \sqrt{98} \)
3. \( \sqrt{150} \)
4. \( \sqrt{200} \)

Simplifying square roots is a fundamental skill in mathematics that makes working with square roots easier and more intuitive. When we simplify a square root, we aim to rewrite it in its simplest form. This process involves breaking down the number inside the square root into its prime factors and then simplifying the expression by removing pairs of factors from under the square root.

Let's explore the steps to simplify square roots:

1. Factorize the number under the square root into its prime factors. For example, \( \sqrt{72} \) can be expressed as \( \sqrt{2 \times 2 \times 2 \times 3 \times 3} \).
2. Identify and group pairs of the same prime factors. In our example, the pairs are \( 2 \times 2 \) and \( 3 \times 3 \).
3. Bring each pair out of the square root. Each pair of factors becomes a single factor outside the square root. Thus, \( \sqrt{2 \times 2 \times 2 \times 3 \times 3} = 2 \times 3 \times \sqrt{2} \).
4. Multiply the numbers outside the square root. For \( \sqrt{72} \), this gives us \( 2 \times 3 = 6 \), resulting in \( 6 \sqrt{2} \).
5. If there are any remaining factors under the square root that cannot be paired, they stay under the square root. In our example, \( \sqrt{2} \) remains inside the square root.

By following these steps, you can simplify any square root. Understanding this process is crucial for solving various mathematical problems more efficiently. Additionally, using a "simplify the square root calculator" can assist in quickly finding the simplified form of more complex square roots, saving time and reducing errors.

In the next sections, we will delve deeper into specific techniques and examples to further illustrate how to simplify square roots effectively.

The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 × 3 = 9.

Square roots can be both positive and negative. For instance, both 3 and -3 are square roots of 9, because (3 × 3) = 9 and (-3 × -3) = 9. However, by convention, the principal square root refers to the non-negative root.

Properties of Square Roots

• Multiplication Property: The square root of a product is equal to the product of the square roots of each factor. For any non-negative numbers a and b:
  \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
• Division Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. For any non-negative numbers a and b (where b is not zero):
  \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)

Perfect Squares

A perfect square is a number that has an integer as its square root. For example, 4, 9, and 16 are perfect squares because their square roots (2, 3, and 4, respectively) are integers. Simplifying square roots often involves recognizing and extracting perfect square factors.

Examples

Here are a few examples to illustrate how to simplify square roots:

• To simplify \(\sqrt{12}\):
  12 can be factored into 4 × 3. Using the multiplication property of square roots:
  \(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\)
• To simplify \(\sqrt{45}\):
  45 can be factored into 9 × 5. Using the multiplication property of square roots:
  \(\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}\)
• To simplify \(\sqrt{18}\):
  18 can be factored into 9 × 2. Using the multiplication property of square roots:
  \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)

Special Cases

When dealing with square roots of fractions or negative numbers, the following rules apply:

• Fractions: Simplify the square root of a fraction by taking the square root of the numerator and the denominator separately. For example:
  \(\sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2}\)
• Negative Numbers: The square root of a negative number involves imaginary numbers. For example:
  \(\sqrt{-1} = i\), where \(i\) is the imaginary unit.

Understanding these basic properties and techniques is essential for simplifying square roots and will be useful in solving more complex mathematical problems involving radicals.

Prime factorization is a method used to simplify square roots by breaking down the number inside the square root into its prime factors. Here are the steps to simplify a square root using prime factorization:

1. Factorize the Number into Prime Factors:

   Begin by dividing the number by the smallest prime number (usually 2) that can exactly divide it without leaving a remainder. Continue this process with the quotient until you reach a prime number. This will give you the prime factors of the number.

   For example, to factorize 72:

   • 72 ÷ 2 = 36
   • 36 ÷ 2 = 18
   • 18 ÷ 2 = 9
   • 9 ÷ 3 = 3
   • 3 ÷ 3 = 1

   So, the prime factors of 72 are: 2³ × 3².

2. Organize the Prime Factors into Pairs:

   Arrange the prime factors and pair identical factors. If a factor does not have a pair, it remains single.

   From the prime factors 2³ × 3²:

   • Pairs: (2, 2), (2), (3, 3)
3. Multiply One Element from Each Pair:

   For each pair of identical primes, select one prime from the pair and multiply them. If a prime remains unpaired, it stays under the square root.

   From the pairs (2, 2) and (3, 3):

   • Multiply one element from each pair: 2 × 3 = 6
4. Calculate the Square Root:

   Multiply the results of the previous step together, and multiply this product by the square root of any leftover unpaired primes to find the square root of the original number.

   The square root of 72 is 6√2.

Here are some more examples:

• Square Root of 144:
  1. Prime Factorization: 144 = 2⁴ × 3²
  2. Pairs: (2, 2), (2, 2), (3, 3)
  3. Multiply one from each pair: 2 × 2 × 3 = 12
  4. √144 = 12
• Square Root of 200:
  1. Prime Factorization: 200 = 2³ × 5²
  2. Pairs: (2, 2), (5, 5)
  3. Multiply one from each pair: 2 × 5 = 10
  4. Since there is an unpaired factor 2, the square root is 10√2

When simplifying square roots, one of the key steps involves identifying and bringing pairs of factors outside the square root. This process makes the expression simpler and easier to work with. Here's a detailed, step-by-step guide on how to do this:

1. Identify the Factors: Start by factorizing the number under the square root into its prime factors.

   Example: To simplify √72, we factorize 72 as follows:

   72 = 2 × 2 × 2 × 3 × 3

2. Pair the Factors: Group the prime factors into pairs.

   In our example: 72 = (2 × 2) × (3 × 3) × 2

3. Bring Pairs Outside the Root: For each pair of factors, take one factor out of the square root.

   Here, we can take one 2 and one 3 out of the square root:

   √72 = √[(2 × 2) × (3 × 3) × 2] = 2 × 3 × √2

   So, √72 simplifies to 6√2.

Let's consider another example to further illustrate this process:

• Example: Simplify √50

  Step 1: Factorize 50 into prime factors: 50 = 2 × 5 × 5

  Step 2: Identify pairs: 50 = 2 × (5 × 5)

  Step 3: Bring the pair of 5s outside the root: √50 = √[2 × (5 × 5)] = 5√2

This method also applies to square roots involving variables:

• Example: Simplify √(18x^2)

  Step 1: Factorize 18 and x^2: 18x^2 = 2 × 3 × 3 × x × x

  Step 2: Identify pairs: 18x^2 = (3 × 3) × (x × x) × 2

  Step 3: Bring the pairs outside: √(18x^2) = 3x√2

By following these steps, you can simplify square roots efficiently, making complex expressions much easier to handle.

When simplifying square roots that contain variables, the same principles used for numerical square roots apply. Here is a detailed, step-by-step guide to help you simplify square roots with variables:

1. Identify the Square Root Expression:

   First, look at the expression inside the square root. For example, consider the expression \( \sqrt{50x^2} \).

2. Factorize the Expression:

   Break down the number and the variable inside the square root into their prime factors. For \( \sqrt{50x^2} \), we have:

   \( 50 = 2 \times 5^2 \) and \( x^2 = (x)^2 \)

   So, \( \sqrt{50x^2} = \sqrt{2 \times 5^2 \times x^2} \).

3. Separate the Factors:

   Use the property of square roots that \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \):

   \( \sqrt{50x^2} = \sqrt{2 \times 5^2 \times x^2} = \sqrt{2} \times \sqrt{5^2} \times \sqrt{x^2} \).

4. Bring Out the Pairs:

   Since \( \sqrt{5^2} = 5 \) and \( \sqrt{x^2} = x \), you can simplify the expression to:

   \( \sqrt{50x^2} = 5x \sqrt{2} \).

Let's look at more examples to solidify the concept:

• Example 1: \( \sqrt{18y^4} \)

  Step 1: Factorize inside the square root:

  \( 18 = 2 \times 3^2 \) and \( y^4 = (y^2)^2 \)

  So, \( \sqrt{18y^4} = \sqrt{2 \times 3^2 \times (y^2)^2} \)

  Step 2: Separate the factors:

  \( \sqrt{18y^4} = \sqrt{2} \times \sqrt{3^2} \times \sqrt{(y^2)^2} \)

  Step 3: Bring out the pairs:

  \( \sqrt{18y^4} = 3y^2 \sqrt{2} \)

• Example 2: \( \sqrt{45a^2b^6} \)

  Step 1: Factorize inside the square root:

  \( 45 = 3^2 \times 5 \), \( a^2 = (a)^2 \), and \( b^6 = (b^3)^2 \)

  So, \( \sqrt{45a^2b^6} = \sqrt{3^2 \times 5 \times (a)^2 \times (b^3)^2} \)

  Step 2: Separate the factors:

  \( \sqrt{45a^2b^6} = \sqrt{3^2} \times \sqrt{5} \times \sqrt{a^2} \times \sqrt{(b^3)^2} \)

  Step 3: Bring out the pairs:

  \( \sqrt{45a^2b^6} = 3ab^3 \sqrt{5} \)

By following these steps, you can simplify any square root expression that contains variables. Practicing with different expressions will help you become more proficient in this process.

Simplifying square roots involves breaking down the number inside the root into its prime factors and pulling out pairs of factors to simplify the expression. Here are detailed examples to illustrate the process:

Example 1: Simplifying \( \sqrt{12} \)

1. Prime factorize the number inside the square root: \( 12 = 2 \times 2 \times 3 \).
2. Group the factors into pairs: \( \sqrt{12} = \sqrt{2^2 \times 3} \).
3. Pull out pairs of factors: \( \sqrt{2^2 \times 3} = 2\sqrt{3} \).

So, \( \sqrt{12} \) simplifies to \( 2\sqrt{3} \).

Example 2: Simplifying \( \sqrt{45} \)

1. Prime factorize the number inside the square root: \( 45 = 3 \times 3 \times 5 \).
2. Group the factors into pairs: \( \sqrt{45} = \sqrt{3^2 \times 5} \).
3. Pull out pairs of factors: \( \sqrt{3^2 \times 5} = 3\sqrt{5} \).

So, \( \sqrt{45} \) simplifies to \( 3\sqrt{5} \).

Example 3: Simplifying \( \sqrt{18} \)

1. Prime factorize the number inside the square root: \( 18 = 2 \times 3 \times 3 \).
2. Group the factors into pairs: \( \sqrt{18} = \sqrt{2 \times 3^2} \).
3. Pull out pairs of factors: \( \sqrt{2 \times 3^2} = 3\sqrt{2} \).

So, \( \sqrt{18} \) simplifies to \( 3\sqrt{2} \).

Example 4: Simplifying \( \sqrt{20} \)

1. Prime factorize the number inside the square root: \( 20 = 2 \times 2 \times 5 \).
2. Group the factors into pairs: \( \sqrt{20} = \sqrt{2^2 \times 5} \).
3. Pull out pairs of factors: \( \sqrt{2^2 \times 5} = 2\sqrt{5} \).

So, \( \sqrt{20} \) simplifies to \( 2\sqrt{5} \).

Example 5: Simplifying \( \sqrt{72} \)

1. Prime factorize the number inside the square root: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
2. Group the factors into pairs: \( \sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{2^2 \times 2 \times 3^2} \).
3. Pull out pairs of factors: \( \sqrt{2^2 \times 2 \times 3^2} = 2 \times 3 \sqrt{2} = 6\sqrt{2} \).

So, \( \sqrt{72} \) simplifies to \( 6\sqrt{2} \).

Example 6: Simplifying \( 2\sqrt{12} + 9\sqrt{3} \)

1. Simplify \( 2\sqrt{12} \):
• Prime factorize \( 12 \): \( 12 = 2 \times 2 \times 3 \).
• Simplify \( \sqrt{12} \): \( \sqrt{12} = 2\sqrt{3} \).
• Combine: \( 2\sqrt{12} = 2 \times 2\sqrt{3} = 4\sqrt{3} \).
2. Add \( 4\sqrt{3} + 9\sqrt{3} \):
• Combine like terms: \( 4\sqrt{3} + 9\sqrt{3} = (4 + 9)\sqrt{3} = 13\sqrt{3} \).

So, \( 2\sqrt{12} + 9\sqrt{3} \) simplifies to \( 13\sqrt{3} \).

Simplifying square roots can sometimes present unique challenges, especially when dealing with special cases. Here, we will discuss several such special cases and the methods to handle them effectively.

1. Square Roots of Perfect Squares

When the radicand (the number inside the square root) is a perfect square, simplifying is straightforward. For example:

• \(\sqrt{16} = 4\) because \(16 = 4^2\).
• \(\sqrt{81} = 9\) because \(81 = 9^2\).

2. Simplifying Square Roots of Fractions

For fractions under a square root, you can simplify by separating the numerator and the denominator:

Example:

• \(\sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2}\)

3. Square Roots of Negative Numbers

Square roots of negative numbers are not real numbers. Instead, they involve imaginary numbers. The imaginary unit \(i\) is defined as \(\sqrt{-1}\). For example:

• \(\sqrt{-9} = 3i\) because \(9 = 3^2\) and \(\sqrt{-1} = i\).

4. Radicals in Denominators

To simplify expressions with square roots in the denominator, rationalize the denominator by multiplying both the numerator and the denominator by the conjugate if necessary:

Example:

• \(\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}\)

5. Nested Radicals

When dealing with nested radicals, where one square root is inside another, simplify the innermost radical first:

Example:

• \(\sqrt{1 + \sqrt{4}} = \sqrt{1 + 2} = \sqrt{3}\)

6. Prime Factorization Method

Sometimes, simplifying involves breaking down the number inside the square root into its prime factors and then simplifying each part:

Example:

• \(\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\)

7. Surds

A surd is an irrational number that cannot be simplified to remove the square root. Examples include:

• \(\sqrt{2}\), \(\sqrt{3}\), \(\sqrt{5}\), etc.

By understanding these special cases, you can approach simplifying square roots with greater confidence and accuracy.

Using a square root calculator can simplify the process of finding square roots, especially for more complex numbers. Here's a detailed guide on how to use a square root calculator effectively:

1. Access the Calculator:

   First, navigate to a reliable online square root calculator. Some popular options include Mathway, Math Warehouse, and Cuemath.

2. Enter the Number:

   Input the number you want to find the square root of into the designated input field. Ensure that the number is correctly entered to avoid errors.

3. Calculate the Square Root:

   Click on the "Calculate" button to process the input. The calculator will display the square root of the number. Most calculators provide both the exact form (simplest radical form) and the decimal approximation.

4. Reset if Needed:

   If you need to calculate another square root, use the "Clear" or "Reset" button to clear the input field and start fresh.

Example Calculations

Here are some example calculations to illustrate how to use a square root calculator:

• Example 1:

  Find the square root of 80.

  Input: 80

  Output: \(\sqrt{80} = 4\sqrt{5} \approx 8.944\)

• Example 2:

  Find the square root of 121.

  Input: 121

  Output: \(\sqrt{121} = 11\)

• Example 3:

  Find the square root of 140.

  Input: 140

  Output: \(\sqrt{140} = 2\sqrt{35} \approx 11.83\)

Tips for Using Square Root Calculators

• Double-check your input to ensure accuracy.
• Familiarize yourself with the calculator's functions, such as resetting and clearing fields.
• Use the calculator for both exact values (simplest radical form) and decimal approximations.

Benefits of Using a Square Root Calculator

Using a square root calculator offers several advantages:

• Accuracy: Minimizes human error in calculations.
• Speed: Provides instant results, saving time.
• Simplicity: Easy to use, even for complex numbers.

Conclusion

Square root calculators are invaluable tools for students and professionals alike. By following the steps outlined above, you can efficiently and accurately determine the square roots of various numbers, whether they are perfect squares or not.

Simplifying square roots offers several significant advantages in mathematical calculations and problem-solving. Here are some key benefits:

• Improves Accuracy: Simplifying square roots reduces complex expressions to their simplest form, minimizing the chance of errors in calculations.
• Enhances Understanding: By simplifying square roots, you gain a better grasp of the underlying mathematical principles, making it easier to understand and solve related problems.
• Saves Time: Simplified expressions are quicker to work with, allowing you to perform calculations more efficiently and effectively.
• Facilitates Further Calculations: Simplified square roots are easier to use in subsequent mathematical operations, such as addition, subtraction, multiplication, and division.
• Reduces Complexity: Simplified square roots eliminate unnecessary complexity, making mathematical expressions cleaner and more manageable.
• Aids in Learning: Learning to simplify square roots helps build foundational skills in algebra and number theory, which are essential for more advanced mathematical studies.
• Improves Presentation: Simplified expressions are more elegant and professional, enhancing the clarity and presentation of mathematical solutions.

In conclusion, simplifying square roots is a valuable skill that not only makes mathematical operations more straightforward but also deepens your understanding and appreciation of the beauty and logic inherent in mathematics.

Simplifying square roots can be tricky, and there are several common mistakes that students often make. Here are some key errors to watch out for and tips on how to avoid them:

• Forgetting to Check for Perfect Squares: Always look for perfect square factors within the number under the square root. For example, in $\backslash (\backslash sqrt\{50\}\backslash )$, recognize that 50 is 25 * 2, and simplify it to $\backslash (5\backslash sqrt\{2\}\backslash )$.
• Rushing Through Simplification: Simplify step by step to avoid mistakes. Breaking down the process into smaller steps can help ensure accuracy. Take your time to factorize the number correctly.
• Ignoring Negative Signs: Remember that the square root of a negative number involves imaginary numbers. For instance, $\backslash (\backslash sqrt\{-4\}\backslash )$ simplifies to $\backslash (2i\backslash )$ where $i$ is the imaginary unit.
• Misapplying Rules: Ensure you use the correct rules for simplification. For example, use $\backslash (\backslash sqrt\{a\}\; \backslash cdot\; \backslash sqrt\{b\}\; =\; \backslash sqrt\{ab\}\backslash )$ correctly by applying it only when the values under the square root are positive.
• Combining Unsimilar Terms: You cannot combine square roots with different radicands. For example, $\backslash (\backslash sqrt\{2\}\; +\; \backslash sqrt\{3\}\backslash )$ cannot be simplified further.

Steps to Avoid Mistakes

1. Identify and list the prime factors of the number under the square root.

2. Group the prime factors into pairs.

3. Move one number from each pair outside the square root.

4. Multiply the numbers outside the square root together.

5. Multiply the numbers left inside the square root together.

6. Write the simplified form as the product of the numbers outside the square root and the square root of the remaining product inside.

Example

Consider simplifying $\backslash (\backslash sqrt\{72\}\backslash )$:

1. Prime factorize 72: $72\; =\; 2\; \backslash times\; 2\; \backslash times\; 2\; \backslash times\; 3\; \backslash times\; 3$.

2. Group the factors into pairs: $(2\; \backslash times\; 2)\; \backslash times\; (3\; \backslash times\; 3)\; \backslash times\; 2$.

3. Move one number from each pair outside the square root: $2\; \backslash times\; 3\; \backslash times\; \backslash sqrt\{2\}$.

4. Simplify the expression: $6\backslash sqrt\{2\}$.

By avoiding these common mistakes and following the correct steps, you can simplify square roots accurately and efficiently.

Simplifying square roots can become more complex when dealing with higher-order roots, expressions with variables, or radical expressions that need further simplification. Here are some advanced techniques to handle such cases:

1. Simplifying Higher-Order Roots

When simplifying higher-order roots, use the general rule that if \( n \) is the root and \( a \) is the radicand, then:

\[ \sqrt[n]{a^n} = a \]

For example:

\[ \sqrt[4]{16y^4} = \sqrt[4]{(2^4)(y^4)} = 2|y| \]

If variables are assumed to be positive, the absolute value can be omitted, yielding:

\[ \sqrt[4]{16y^4} = 2y \]

2. Combining Radicals

Use the product and quotient rules to combine multiple radical expressions into a single radical:

• Product Rule: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\)
• Quotient Rule: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)

Example of combining radicals:

\[ \sqrt{12} \cdot \sqrt{3} = \sqrt{12 \cdot 3} = \sqrt{36} = 6 \]

3. Simplifying Radicals with Variables

To simplify radicals involving variables, identify perfect squares (or higher-order perfect powers) within the radicand and factor them out:

Example:

\[ \sqrt{50x^2y^3} \]

Factor the radicand:

\[ \sqrt{25 \cdot 2 \cdot x^2 \cdot y^2 \cdot y} = \sqrt{25} \cdot \sqrt{2} \cdot \sqrt{x^2} \cdot \sqrt{y^2} \cdot \sqrt{y} = 5x y \sqrt{2y} \]

4. Rationalizing Denominators

To simplify expressions with radicals in the denominator, multiply the numerator and the denominator by a suitable radical to eliminate the radical in the denominator:

Example:

\[ \frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2} \]

5. Using Least Common Multiple (LCM) in Mixed Roots

When dealing with expressions containing mixed roots, convert them to a common root using the least common multiple (LCM) of the indices:

Example:

\[ 2 \sqrt[3]{4} \cdot 3 \sqrt{2} \]

Convert to a common root (6th root in this case):

\[ 2 \sqrt[3]{4} = 2 \sqrt[6]{4^2} = 2 \sqrt[6]{16} \]

\[ 3 \sqrt{2} = 3 \sqrt[6]{2^3} = 3 \sqrt[6]{8} \]

Now multiply the expressions:

\[ 2 \sqrt[6]{16} \cdot 3 \sqrt[6]{8} = 6 \sqrt[6]{128} \]

Practice Problems

1. Simplify \(\sqrt{72x^4y^5}\)
2. Simplify \(\sqrt{\frac{50}{2x}}\)
3. Simplify \( \sqrt[3]{27a^6b^3} \)

Utilizing these advanced techniques can make simplifying complex radical expressions more manageable and accurate.

Here are some practice problems to help you master simplifying square roots. Follow the steps provided to simplify each expression.

Problem 1: Simplify \( \sqrt{72} \)

1. Factor 72 into prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
2. Group the prime factors into pairs: \( (2 \times 2) \times 2 \times (3 \times 3) \).
3. Take one number from each pair outside the square root: \( 2 \times 3 \times \sqrt{2} \).
4. Simplified form: \( 6\sqrt{2} \).

Problem 2: Simplify \( \sqrt{288} \)

1. Factor 288 into prime factors: \( 288 = 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \).
2. Group the prime factors into pairs: \( (2 \times 2) \times (2 \times 2) \times 2 \times (3 \times 3) \).
3. Take one number from each pair outside the square root: \( 2 \times 2 \times 3 \times \sqrt{2} \).
4. Simplified form: \( 12\sqrt{2} \).

Problem 3: Simplify \( \sqrt{108} \)

1. Factor 108 into prime factors: \( 108 = 2 \times 2 \times 3 \times 3 \times 3 \).
2. Group the prime factors into pairs: \( (2 \times 2) \times (3 \times 3) \times 3 \).
3. Take one number from each pair outside the square root: \( 2 \times 3 \times \sqrt{3} \).
4. Simplified form: \( 6\sqrt{3} \).

Problem 4: Simplify \( \sqrt{200} \)

1. Factor 200 into prime factors: \( 200 = 2 \times 2 \times 2 \times 5 \times 5 \).
2. Group the prime factors into pairs: \( (2 \times 2) \times 2 \times (5 \times 5) \).
3. Take one number from each pair outside the square root: \( 2 \times 5 \times \sqrt{2} \).
4. Simplified form: \( 10\sqrt{2} \).

Problem 5: Simplify \( \sqrt{45} \)

1. Factor 45 into prime factors: \( 45 = 3 \times 3 \times 5 \).
2. Group the prime factors into pairs: \( (3 \times 3) \times 5 \).
3. Take one number from each pair outside the square root: \( 3 \times \sqrt{5} \).
4. Simplified form: \( 3\sqrt{5} \).

Additional Problems

Try solving the following problems on your own:

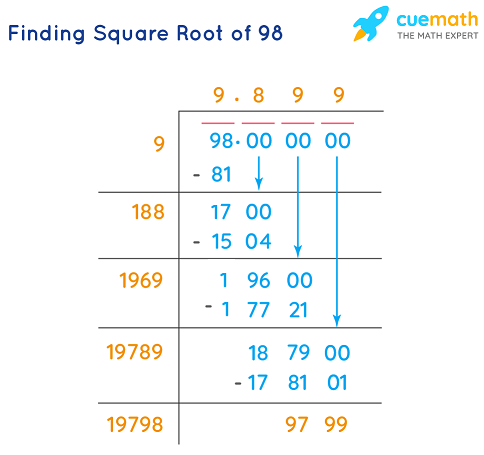
• Simplify \( \sqrt{98} \)
• Simplify \( \sqrt{245} \)
• Simplify \( \sqrt{360} \)

Check your solutions using the same steps outlined above. Practice makes perfect!

• Can a number have more than one square root?

  Yes, every positive number has two square roots: a positive root (the principal root) and a negative root. For example, the square roots of 16 are 4 and -4.

• What is the square root of -1?

  The square root of -1 is an imaginary number, denoted as \(i\). Thus, the square roots of -1 are \(i\) and \(-i\).

• What is the square root of 0?

  The square root of 0 is unique and equals 0. Both +0 and -0 are equivalent to 0.

• How do I find the square root using a calculator?

  Most calculators have a square root button, denoted by \(\sqrt{}\) or "sqrt". Enter the number and press this button to get the square root.

• Can I calculate square roots without a calculator?

  Yes, you can use methods like prime factorization or estimation to find square roots manually.

• What are some properties of square roots?

  Square roots follow specific properties:

  • \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
  • \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)

• Why are square roots important in mathematics?

  Square roots are essential in various mathematical fields, including algebra, geometry, and calculus, helping solve equations and understand geometric relationships.

When it comes to simplifying square roots, various resources and tools can significantly aid the learning process. Below are some recommended resources and tools that can help:

Online Calculators

• This tool allows users to enter any square root expression and get a step-by-step solution. It also provides both exact and decimal forms for non-perfect squares.

• dCode offers a detailed square root calculator that can handle complex roots and provides explanations for each step in the simplification process.

• This calculator helps users find the square root and simplifies expressions by factoring out squares. It also includes educational content on the properties and methods of simplifying square roots.

Educational Websites

• Khan Academy provides video tutorials and practice exercises on simplifying square roots, helping learners to understand and apply various simplification techniques.

• Purplemath offers comprehensive lessons on radicals, including simplifying square roots. The site provides clear explanations and examples for better understanding.

Mobile Apps

• Available on both iOS and Android, the Mathway app allows users to solve square root problems on-the-go by simply taking a photo of the problem or entering it manually.

• This app uses the phone's camera to recognize and solve mathematical problems, including simplifying square roots, providing step-by-step solutions.

Textbooks and Guides

• Pre-Algebra by Richard Rusczyk

  This book includes a detailed section on simplifying square roots, offering both theoretical explanations and practical exercises.

• The Art of Problem Solving series

  These books provide a deep dive into mathematical concepts, including radicals and square roots, with numerous practice problems and solutions.