Topic simplify square root of 72: Welcome to our comprehensive guide on how to simplify the square root of 72. This article will walk you through each step of the simplification process, ensuring you understand the concepts and techniques needed to achieve the simplest form of √72. Let’s dive in and make simplifying square roots easy and fun!
Table of Content
- Simplifying the Square Root of 72
- Introduction
- Understanding Square Roots
- What is the Square Root of 72?
- Mathematical Representation of √72
- Steps to Simplify the Square Root of 72
- Factorization Method
- Prime Factorization Method
- Long Division Method
- Decimal Form of the Square Root of 72
- Properties of √72
- Rational and Irrational Numbers
- Simplified Radical Form of √72
- Practical Applications of Square Roots
- Examples and Practice Problems
- FAQs
- Conclusion
- YOUTUBE: Video này giới thiệu cách đơn giản hóa căn bậc hai của số 72 một cách dễ hiểu và chi tiết, phù hợp cho những ai muốn học toán.
Simplifying the Square Root of 72
In this section, we will simplify the square root of 72 step-by-step, making it easy to understand and apply. The simplification process involves breaking down the number inside the square root into its prime factors.
Step-by-Step Simplification Process
First, find the prime factorization of 72. The prime factors of 72 are:
\[ 72 = 2 \times 36 \]
\[ 36 = 2 \times 18 \]
\[ 18 = 2 \times 9 \]
\[ 9 = 3 \times 3 \]
So, the prime factorization of 72 is:
\[ 72 = 2^3 \times 3^2 \]
Next, apply the square root to the prime factors:
\[ \sqrt{72} = \sqrt{2^3 \times 3^2} \]
Separate the factors under the square root:
\[ \sqrt{72} = \sqrt{2^2 \times 2 \times 3^2} \]
Simplify the square root by taking out pairs of prime factors:
\[ \sqrt{72} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{2} \]
\[ \sqrt{72} = 2 \times 3 \times \sqrt{2} \]
Finally, multiply the simplified factors:
\[ \sqrt{72} = 6 \sqrt{2} \]
Thus, the simplified form of the square root of 72 is:
Additional Tips and Tricks
- Remember that simplifying square roots often involves finding pairs of prime factors.
- Practice with other numbers to become more comfortable with the process.
- Use tools like prime factorization calculators to check your work.

READ MORE:
Introduction
Simplifying the square root of 72 involves breaking down the number into its prime factors to make it easier to handle. This process not only simplifies calculations but also enhances your understanding of square roots. By the end of this guide, you will be able to simplify √72 to its simplest form, making math both fun and approachable.
Understanding Square Roots
Square roots are mathematical expressions that represent a value which, when multiplied by itself, gives the original number. For example, the square root of 72 is denoted as \(\sqrt{72}\). Understanding square roots involves recognizing the parts of the radical expression:
- Radicand: The number inside the radical symbol. In \(\sqrt{72}\), 72 is the radicand.
- Radical Symbol: The symbol \(\sqrt{}\) used to denote the square root.
To simplify square roots, we often use the prime factorization method. This involves breaking down the radicand into its prime factors, which can then be grouped into pairs to simplify the expression. This process helps in reducing complex radical expressions to their simplest forms, making calculations easier and more intuitive.
What is the Square Root of 72?
The square root of 72 is a value that, when multiplied by itself, results in the number 72. Mathematically, the square root of 72 is represented as \(\sqrt{72}\). To understand this concept better, let’s break it down:
The square root symbol \(\sqrt{}\) is known as the radical symbol, and the number underneath it is called the radicand. Here, 72 is the radicand.
When we simplify \(\sqrt{72}\), we look for perfect square factors of 72. In this case, 36 is the largest perfect square factor of 72, since \(36 \times 2 = 72\).
Using the property of square roots, we can split \(\sqrt{72}\) into \(\sqrt{36 \times 2}\), which further simplifies to \(\sqrt{36} \times \sqrt{2}\).
Since \(\sqrt{36} = 6\), we get \(\sqrt{72} = 6 \times \sqrt{2}\).
Therefore, the simplified form of the square root of 72 is \(6\sqrt{2}\). This form is much simpler to work with and is essential for solving various mathematical problems efficiently.
Mathematical Representation of √72
The square root of 72 can be represented in various mathematical forms. Here, we'll explore these representations in detail using MathJax for better clarity.
- Radical Form: The simplest form of the square root of 72 is represented using the radical symbol (√). Thus, we write it as:
\(\sqrt{72}\)
- Exponential Form: The square root of 72 can also be expressed using exponents. In this form, it is written as:
\(72^{\frac{1}{2}}\)
- Decimal Form: The approximate value of the square root of 72 in decimal form is:
\(\sqrt{72} \approx 8.485\)
Next, let's simplify the square root of 72 using the factorization method:
- Factorize 72 into its prime factors:
\(72 = 2^3 \times 3^2\)
- Identify the pairs of prime factors:
\(72 = (2^2 \times 3^2) \times 2\)
- Take the square root of the pairs of prime factors:
\(\sqrt{72} = \sqrt{(2^2 \times 3^2) \times 2} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
Therefore, the simplified radical form of the square root of 72 is:
\(\sqrt{72} = 6\sqrt{2}\)
In summary, the square root of 72 can be represented in multiple forms, each useful in different mathematical contexts. The exact form \(6\sqrt{2}\) is particularly important in simplifying expressions and solving equations.

Steps to Simplify the Square Root of 72
To simplify the square root of 72, follow these detailed steps:
-
List Factors of 72:
The factors of 72 are:
- 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
-
Identify Perfect Squares:
From the list of factors, the perfect squares are:
- 1, 4, 9, 36
-
Divide by the Largest Perfect Square:
Divide 72 by the largest perfect square identified, which is 36:
\[ 72 \div 36 = 2 \]
-
Rewrite the Square Root Expression:
Express the square root of 72 using the result from the division:
\[ \sqrt{72} = \sqrt{36 \times 2} \]
-
Apply the Product Rule for Radicals:
Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):
\[ \sqrt{72} = \sqrt{36} \times \sqrt{2} \]
-
Calculate the Square Root of the Perfect Square:
The square root of 36 is 6:
\[ \sqrt{36} = 6 \]
-
Combine the Results:
Multiply the results to get the simplest form:
\[ \sqrt{72} = 6 \times \sqrt{2} = 6\sqrt{2} \]
Therefore, the simplified form of \(\sqrt{72}\) is \(6\sqrt{2}\).
Factorization Method
The factorization method involves breaking down a number into its prime factors and then simplifying the square root by grouping the factors into pairs. Here's a detailed, step-by-step process to simplify the square root of 72 using the factorization method:
-
Prime Factorization: First, find the prime factors of 72.
- 72 ÷ 2 = 36
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
So, the prime factors of 72 are: \( 2^3 \times 3^2 \).
-
Organize the Prime Factors: Arrange the prime factors and pair identical factors.
Pairs: \((2, 2), (2), (3, 3)\)
-
Multiply One Element from Each Pair: For each pair of identical primes, select one prime and multiply them.
From the pairs: \(2 \times 3 = 6\)
-
Calculate the Square Root: Multiply the result from the previous step by the square root of any leftover unpaired primes.
The unpaired prime is \(2\).
Therefore, the square root of 72 is \(6 \sqrt{2}\).
Thus, the simplified form of \(\sqrt{72}\) is \(6 \sqrt{2}\).
Prime Factorization Method
The prime factorization method is a systematic approach to simplify the square root of a number by expressing it as a product of its prime factors. Here are the detailed steps to simplify the square root of 72 using the prime factorization method:
-
First, determine the prime factors of 72. The prime factorization of 72 is:
\[ 72 = 2 \times 2 \times 2 \times 3 \times 3 \]
-
Next, group the prime factors in pairs:
\[ 72 = (2 \times 2) \times 2 \times (3 \times 3) \]
-
Take the square root of both sides:
\[ \sqrt{72} = \sqrt{(2 \times 2) \times 2 \times (3 \times 3)} \]
We can simplify the pairs of factors outside the square root:
\[ \sqrt{72} = \sqrt{4 \times 2 \times 9} \]
-
Since \(\sqrt{4} = 2\) and \(\sqrt{9} = 3\), we can simplify further:
\[ \sqrt{72} = 2 \times 3 \times \sqrt{2} \]
-
Finally, multiply the simplified terms outside the square root:
\[ \sqrt{72} = 6 \sqrt{2} \]
Thus, the simplified form of \(\sqrt{72}\) using the prime factorization method is \(6 \sqrt{2}\).
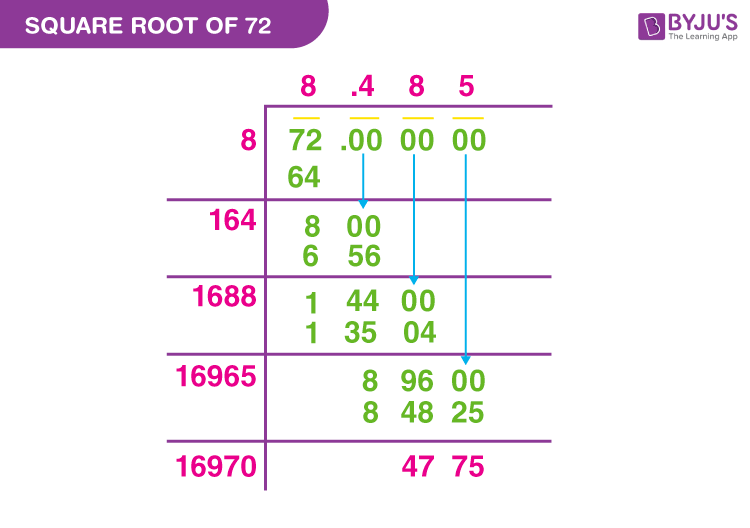
Long Division Method
The long division method is a technique used to find the square root of a number by approximating it step by step. Below is a detailed step-by-step guide to simplify the square root of 72 using the long division method.
- Write the number 72 as 72.00000000 (adding pairs of zeros).
- Group the digits in pairs from the decimal point: 72 00 00 00 00.
- Find the largest number whose square is less than or equal to the first group (72). In this case, it is 8, since \(8^2 = 64\) and \(9^2 = 81\).
- Write 8 as the first digit of the quotient. Subtract 64 from 72 to get the remainder 8. Bring down the next pair of zeros to make it 800.
- Double the quotient (8) and write it as 16. Now, find a digit X such that 16X * X is less than or equal to 800. In this case, the digit is 4 because \(164 * 4 = 656\) and \(165 * 5 = 825\) which is greater than 800.
- Write 4 next to 8 in the quotient (making it 8.4). Subtract 656 from 800 to get the remainder 144. Bring down the next pair of zeros to make it 14400.
- Double the quotient (84) and write it as 168. Find a digit X such that 168X * X is less than or equal to 14400. The digit is 8 because \(1688 * 8 = 13504\) and \(1689 * 9 = 15121\).
- Write 8 next to 84 in the quotient (making it 8.48). Subtract 13504 from 14400 to get the remainder 896. Bring down the next pair of zeros to make it 89600.
- Repeat the process to obtain more decimal places as needed.
The square root of 72 using the long division method is approximately 8.485. You can continue the process to get a more precise value.

Decimal Form of the Square Root of 72
The decimal form of the square root of 72 can be obtained through the long division method, which provides a non-repeating, non-terminating decimal. Here’s how we find the decimal form step by step:
-
First, pair the digits of 72 from right to left, which gives us 72. We consider this as a whole number for the calculation.
-
Find the largest number whose square is less than or equal to 72. Since \(8^2 = 64\) and \(9^2 = 81\), we choose 8.
-
Set 8 as the initial quotient and divisor. Subtract \(64\) (which is \(8 \times 8\)) from 72, leaving a remainder of 8. Bring down a pair of zeros, making it 800.
-
Double the quotient (8), getting 16. Now, find a digit \(X\) such that \(16X \times X \leq 800\). The largest possible digit is 4, since \(164 \times 4 = 656\). Subtract 656 from 800 to get a remainder of 144. Bring down another pair of zeros to make it 14400.
-
Double the quotient (84) to get 168. Find a digit \(Y\) such that \(168Y \times Y \leq 14400\). The largest possible digit is 8, since \(1688 \times 8 = 13504\). Subtract 13504 from 14400 to get a remainder of 896. Bring down another pair of zeros to make it 89600.
-
Double the quotient (848) to get 1696. Find a digit \(Z\) such that \(1696Z \times Z \leq 89600\). The largest possible digit is 5, since \(16965 \times 5 = 84825\). Subtract 84825 from 89600 to get a remainder of 4775. Bring down another pair of zeros to make it 477500.
Continue this process to get more digits. The approximate value of the square root of 72 is:
\[
\sqrt{72} \approx 8.48528137423857
\]
Rounding to different decimal places:
- Nearest tenth: \(8.5\)
- Nearest hundredth: \(8.49\)
- Nearest thousandth: \(8.485\)
Properties of √72
The square root of 72 has several interesting properties. Understanding these properties helps in comprehending the nature and behavior of square roots in mathematics.
1. Irrational Number
The square root of 72 is an irrational number. This means it cannot be expressed as a simple fraction and its decimal form goes on forever without repeating. Mathematically, we write:
\[\sqrt{72} \approx 8.48528137423857\]
Since this is a non-repeating, non-terminating decimal, √72 is irrational.
2. Simplified Radical Form
The square root of 72 can be simplified using prime factorization. The simplified form is:
\[\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\]
3. Approximation
For practical purposes, the square root of 72 is often approximated. Common approximations include:
- To the nearest tenth: \(\sqrt{72} \approx 8.5\)
- To the nearest hundredth: \(\sqrt{72} \approx 8.49\)
- To the nearest thousandth: \(\sqrt{72} \approx 8.485\)
4. Exponential Form
The square root of 72 can also be expressed in its exponential form:
\[\sqrt{72} = 72^{1/2}\]
5. Not a Perfect Square
The number 72 is not a perfect square because its square root is not an integer. Perfect squares are numbers like 1, 4, 9, 16, etc., where the square root is a whole number.
6. Relation to Area
In geometry, if you have a square with an area of 72 square units, the length of each side of the square is the square root of 72:
\[\text{Side length} = \sqrt{72} \approx 8.485 \text{ units}\]
Similarly, for a circle with an area of 72π square units, the radius is:
\[r = \sqrt{72} \approx 8.485 \text{ units}\]
7. Multiplication Property
The square root of a product is the product of the square roots of the factors:
\[\sqrt{ab} = \sqrt{a} \times \sqrt{b}\]
For example:
\[\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\]
8. Real Number
The square root of 72 is a real number, meaning it is a value that represents a quantity along a continuous number line.
Understanding these properties provides a comprehensive view of the nature of the square root of 72, aiding in various mathematical and practical applications.
Rational and Irrational Numbers
To understand whether the square root of 72 (\(\sqrt{72}\)) is a rational or irrational number, we first need to define these terms.
Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction \(\frac{p}{q}\) of two integers, where \(p\) and \(q\) are integers and \(q \neq 0\). The decimal form of a rational number either terminates (ends) or repeats.
- Examples of rational numbers: \( \frac{1}{2} = 0.5 \), \( \frac{2}{3} = 0.666\ldots \) (repeating).
Irrational Numbers
An irrational number cannot be expressed as a simple fraction. Its decimal form does not terminate or repeat.
- Examples of irrational numbers: \( \pi \approx 3.14159\ldots \), \( \sqrt{2} \approx 1.41421\ldots \).
Determining if \(\sqrt{72}\) is Rational or Irrational
To determine whether \(\sqrt{72}\) is rational or irrational, let's examine its decimal form:
\(\sqrt{72} \approx 8.48528137423857\ldots\)
The decimal form of \(\sqrt{72}\) does not terminate or repeat, which indicates that it cannot be expressed as a simple fraction.
Thus, \(\sqrt{72}\) is an irrational number.
Properties of Irrational Numbers
Irrational numbers have several important properties:
- They cannot be exactly represented as fractions of integers.
- Their decimal expansions are infinite and non-repeating.
- When added to or multiplied by rational numbers, the result is usually irrational (e.g., \(1 + \sqrt{2}\) or \(2 \times \sqrt{3}\)).
Summary
Since \(\sqrt{72}\) does not have a terminating or repeating decimal expansion, it is classified as an irrational number. Understanding the difference between rational and irrational numbers helps in many areas of mathematics, including algebra and number theory.
Simplified Radical Form of √72
To find the simplified radical form of the square root of 72, we use the prime factorization method. Here is a step-by-step process:
First, write the number 72 as a product of its prime factors:
\[ 72 = 2 \times 36 \]
Since 36 is a perfect square, we can further break it down:
\[ 72 = 2 \times 6^2 \]
Now, apply the property of square roots which states that \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):
\[ \sqrt{72} = \sqrt{2 \times 6^2} \]
Separate the square root of the perfect square and the other factor:
\[ \sqrt{2 \times 6^2} = \sqrt{2} \times \sqrt{6^2} \]
Simplify the square root of the perfect square (since \(\sqrt{6^2} = 6\)):
\[ \sqrt{2} \times 6 = 6\sqrt{2} \]
Thus, the simplified radical form of \(\sqrt{72}\) is:
\[ \sqrt{72} = 6\sqrt{2} \]
This means that the square root of 72 can be simplified to 6 times the square root of 2.

Practical Applications of Square Roots
Square roots are used in various practical applications across different fields. Here are some key examples:
- Geometry and Trigonometry: Square roots are essential in geometry for calculating the lengths of sides in right triangles using the Pythagorean theorem. For example, in a right triangle with legs of lengths \(a\) and \(b\), the hypotenuse \(c\) is given by \(c = \sqrt{a^2 + b^2}\).
- Physics: Square roots are used in formulas involving kinetic energy, wave speeds, and distances. For instance, the formula for the period \(T\) of a pendulum is \(T = 2\pi \sqrt{\frac{L}{g}}\), where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity.
- Finance: In finance, square roots are used to calculate the standard deviation of investment returns, which is a measure of risk. The formula involves finding the square root of the average squared deviations from the mean.
- Engineering: Engineers use square roots in structural analysis and design. For example, the natural frequency \(f\) of a vibrating system is given by \(f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}\), where \(k\) is the stiffness of the system and \(m\) is the mass.
- Computer Graphics: Square roots are used in computer graphics for calculating distances between points and normalizing vectors. This is crucial for rendering 3D models and creating realistic visual effects.
- Statistics: In statistics, square roots are used in various calculations, such as the standard error of the mean, which is \(SE = \frac{s}{\sqrt{n}}\), where \(s\) is the sample standard deviation and \(n\) is the sample size.
These examples highlight the importance of square roots in solving real-world problems and their pervasive use in different domains.
Examples and Practice Problems
Here are some examples and practice problems to help you understand how to simplify the square root of 72.
Example 1: Simplifying √72
Let's simplify the square root of 72 step by step:
- Factorize 72 into its prime factors:
- \( 72 = 2 \times 36 \)
- \( 36 = 2 \times 18 \)
- \( 18 = 2 \times 9 \)
- \( 9 = 3 \times 3 \)
- Apply the square root to each factor:
- \( \sqrt{72} = \sqrt{2^3 \times 3^2} \)
- \( \sqrt{72} = \sqrt{2^2 \times 2 \times 3^2} \)
- Separate the perfect squares from the non-perfect squares:
- \( \sqrt{72} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{2} \)
- \( \sqrt{72} = 2 \times 3 \times \sqrt{2} \)
- \( \sqrt{72} = 6\sqrt{2} \)
Practice Problems
Try simplifying the following square roots using the same method:
- \( \sqrt{50} \)
- \( \sqrt{98} \)
- \( \sqrt{128} \)
- \( \sqrt{200} \)
Example 2: Solving \(\sqrt{72}\) Using Prime Factorization
Another way to simplify the square root of 72 is by using prime factorization:
- Write 72 as a product of its prime factors:
- \( 72 = 2^3 \times 3^2 \)
- Group the prime factors into pairs:
- \( 72 = (2 \times 2) \times 2 \times (3 \times 3) \)
- Simplify each pair:
- \( \sqrt{72} = \sqrt{(2^2) \times 2 \times (3^2)} \)
- \( \sqrt{72} = 2 \times 3 \times \sqrt{2} \)
- \( \sqrt{72} = 6\sqrt{2} \)
Practice Problem Solutions
| Problem | Solution |
|---|---|
| \( \sqrt{50} \) | \( \sqrt{50} = \sqrt{2 \times 25} = \sqrt{2} \times \sqrt{25} = 5\sqrt{2} \) |
| \( \sqrt{98} \) | \( \sqrt{98} = \sqrt{2 \times 49} = \sqrt{2} \times \sqrt{49} = 7\sqrt{2} \) |
| \( \sqrt{128} \) | \( \sqrt{128} = \sqrt{2^7} = \sqrt{2^6 \times 2} = 8\sqrt{2} \) |
| \( \sqrt{200} \) | \( \sqrt{200} = \sqrt{2^3 \times 5^2} = \sqrt{2^2 \times 2 \times 5^2} = 10\sqrt{2} \) |
FAQs
-
Q: What is the square root of 72?
A: The square root of 72 is approximately 8.485. In its simplest radical form, it is \(6\sqrt{2}\).
-
Q: How do you simplify the square root of 72?
A: To simplify \( \sqrt{72} \):
- Find the prime factorization of 72, which is \(2^3 \times 3^2\).
- Group the prime factors into pairs: \((2 \times 2) \times (3 \times 3) \times 2\).
- Take one factor from each pair outside the square root: \(2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
Q: Is the square root of 72 a rational number?
A: No, the square root of 72 is not a rational number. It is an irrational number because its decimal form is non-repeating and non-terminating: approximately 8.48528137424...
-
Q: How can you represent the square root of 72 in exponential form?
A: The square root of 72 can be expressed in exponential form as \(72^{1/2}\).
-
Q: What are the properties of the square root of 72?
- The square root of 72 is approximately 8.485.
- In its simplest radical form, it is \(6\sqrt{2}\).
- The square root of 72 is an irrational number.
- 72 is an even composite number, and its prime factors include both even and odd numbers.
Conclusion
Simplifying the square root of 72 provides a clear understanding of both the radical and decimal forms of the number. By breaking down 72 into its prime factors and identifying the largest perfect square factor, we simplify to . This method not only aids in simplifying other square roots but also enhances our mathematical skills.
The methods used, such as prime factorization and long division, are fundamental techniques in mathematics, offering a structured approach to problem-solving. The decimal form of the square root of 72 is approximately 8.485, which is useful in various real-life applications where precision is crucial.
Understanding the properties of square roots, especially in distinguishing between rational and irrational numbers, enriches our comprehension of number theory. The square root of 72 being an irrational number exemplifies the nature of non-repeating, non-terminating decimals.
By mastering these concepts, we not only simplify the square root of 72 but also build a strong foundation for more advanced mathematical explorations. The practical applications of square roots in areas such as geometry, physics, and engineering highlight the importance of these skills in academic and professional settings.
In conclusion, simplifying the square root of 72 demonstrates the beauty of mathematics in transforming complex expressions into simpler forms, making them more accessible and easier to understand. This process emphasizes the power of mathematical reasoning and the importance of continuous learning and practice.
Video này giới thiệu cách đơn giản hóa căn bậc hai của số 72 một cách dễ hiểu và chi tiết, phù hợp cho những ai muốn học toán.
Cách Tốt Nhất Để Đơn Giản Hóa Căn Bậc Hai của Một Số, Căn Bậc Hai (72)
READ MORE:
Video này hướng dẫn cách tính căn bậc hai của số 72 một cách chi tiết và dễ hiểu, phù hợp cho những ai muốn học toán.
Cách Tính Căn Bậc Hai của 72: Căn Bậc Hai (72)













