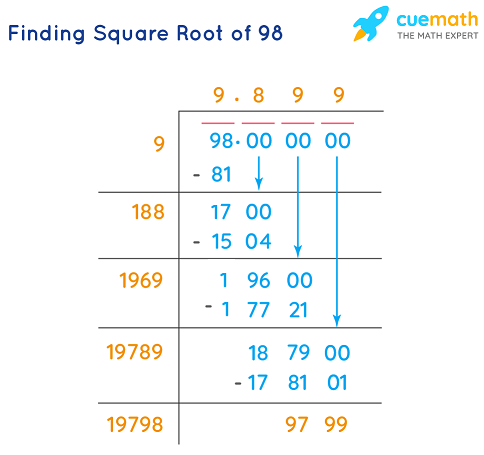
Topic solve square root equations calculator: Discover the best methods and tools to solve square root equations efficiently. Our comprehensive guide introduces you to online calculators that simplify the process, offering step-by-step solutions to help you understand and master square root equations. Perfect for students and math enthusiasts looking to enhance their problem-solving skills.
Table of Content
- Square Root Equation Solver
- Introduction to Square Root Equations
- Understanding Square Roots
- Basic Properties of Square Roots
- Simplifying Square Root Expressions
- Common Techniques and Methods
- Using Online Square Root Calculators
- Examples of Solved Square Root Equations
- Tips for Solving Complex Square Root Problems
- Common Mistakes and How to Avoid Them
- Advanced Topics in Square Root Equations
- Practice Problems and Solutions
- Additional Resources and References
- YOUTUBE:
Square Root Equation Solver
Solving square root equations can be simplified using various online calculators that provide step-by-step solutions. Here is a guide to help you understand how to solve square root equations using these tools.
Steps to Solve Square Root Equations
- Enter the equation with the square root into the calculator. Make sure the equation is in its correct form.
- Click on the 'Calculate' button to process the equation.
- View the step-by-step solution provided by the calculator. These steps typically involve isolating the square root and squaring both sides of the equation to remove the square root.
Example of Solving a Square Root Equation
Consider the equation: \(\sqrt{x+4} = 5 - \sqrt{x-1}\)
- Square both sides to remove the square root:
- \((\sqrt{x+4})^2 = (5 - \sqrt{x-1})^2\)
- \(x+4 = 25 - 10\sqrt{x-1} + x - 1\)
- Simplify and solve for \(x\):
- \(x + 4 = 24 - 10\sqrt{x-1} + x\)
- \(4 = 24 - 10\sqrt{x-1}\)
- \(10\sqrt{x-1} = 20\)
- \(\sqrt{x-1} = 2\)
- \(x - 1 = 4\)
- \(x = 5\)
Simplifying Square Roots
To simplify square roots, find the factors of the number under the square root and check if any of them are perfect squares. For example:
- \(\sqrt{27} = \sqrt{9 \times 3} = \sqrt{9} \times \sqrt{3} = 3\sqrt{3}\)
- \(\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2}\)
Using Online Calculators
There are several online calculators available to help with solving square root equations. Some of the most popular include:
- : Enter your problem and get a step-by-step solution.
- : Provides detailed explanations for each step.
- : Simplifies and solves square root problems.

READ MORE:
Introduction to Square Root Equations
Square root equations are mathematical expressions that involve the square root of a variable or an expression. These types of equations often appear in algebra and are essential for understanding more complex mathematical concepts. Solving square root equations requires isolating the square root on one side and then squaring both sides of the equation to eliminate the radical. Here's a step-by-step guide to solving square root equations:
- Isolate the square root: Ensure that the square root term is by itself on one side of the equation.
- Square both sides: To remove the square root, square both sides of the equation. This will give you a new equation without the radical.
- Simplify the equation: Solve the resulting equation using standard algebraic methods. This may involve combining like terms, factoring, or using the quadratic formula.
- Check your solutions: Substitute your solutions back into the original equation to ensure they do not produce extraneous results. Squaring both sides can sometimes introduce solutions that are not valid for the original equation.
Let's consider an example to illustrate these steps:
- Example: Solve the equation .
- Isolate the square root: .
- Square both sides: .
- Simplify: .
- Check the solution: Substitute back into the original equation to verify.
By following these steps, you can effectively solve square root equations and verify that your solutions are correct.
Understanding Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because \(5 \times 5 = 25\). The square root is represented by the radical symbol (√).
Square roots can be categorized into two types:
- Perfect Squares: Numbers that are squares of integers. For instance, 1, 4, 9, 16, and 25 are perfect squares because they can be written as \(1^2, 2^2, 3^2, 4^2,\) and \(5^2\) respectively.
- Non-Perfect Squares: Numbers that are not squares of integers, such as 2, 3, 5, and 7.
Properties of Square Roots
Square roots have several important properties that are useful in simplifying and solving equations:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^2 = a\)
Steps to Simplify Square Roots
- Identify if the number under the square root is a perfect square. If it is, then simply take the square root.
- If the number is not a perfect square, factor the number into its prime factors and look for pairs of the same factor.
- Use the property \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) to separate the factors under the square root.
- Simplify the expression by taking out pairs of factors from under the square root.
For example, to simplify \(\sqrt{18}\):
- Factor 18 into \(2 \times 3 \times 3\).
- Pair the threes and use the property \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\).
- This gives \(\sqrt{18} = \sqrt{3^2 \cdot 2} = 3\sqrt{2}\).
Why Simplify Square Roots?
Simplifying square roots is essential in various mathematical operations, including solving equations, performing algebraic manipulations, and in calculus. Simplified forms are easier to work with and understand.
Example Problems
Let's look at a couple of examples to solidify our understanding:
- Simplify \(\sqrt{50}\):
- Factor 50 into \(2 \times 5 \times 5\).
- Identify pairs of factors: \(5^2\).
- Simplify using the property: \(\sqrt{50} = \sqrt{5^2 \cdot 2} = 5\sqrt{2}\).
- Simplify \(\sqrt{72}\):
- Factor 72 into \(2 \times 2 \times 2 \times 3 \times 3\).
- Identify pairs of factors: \(2^2 \cdot 3^2\).
- Simplify using the property: \(\sqrt{72} = \sqrt{2^2 \cdot 3^2 \cdot 2} = 2 \cdot 3 \sqrt{2} = 6\sqrt{2}\).
Basic Properties of Square Roots
Square roots are fundamental mathematical operations with several key properties. Understanding these properties is crucial for simplifying and solving square root equations.
- Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). It is denoted as \(\sqrt{x}\).
- Non-negative Values: For any real number \(x\), \(\sqrt{x} \geq 0\). The principal square root is always non-negative.
- Product Property: The square root of a product is the product of the square roots: \[ \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \]
- Quotient Property: The square root of a quotient is the quotient of the square roots: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \] for \(b \neq 0\).
- Power of a Square Root: The square root of a number can be expressed as the number raised to the power of one-half: \[ \sqrt{x} = x^{1/2} \]
- Square of a Square Root: Squaring a square root returns the original number: \[ (\sqrt{x})^2 = x \]
- Simplifying Square Roots: To simplify a square root, factor the number into its prime factors and pair the identical factors. For example: \[ \sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2} \]
- Addition and Subtraction: Square roots can only be added or subtracted if they have the same radicand (the number inside the square root). For example: \[ \sqrt{3} + 2\sqrt{3} = 3\sqrt{3} \] However, \(\sqrt{2} + \sqrt{3}\) cannot be simplified further.
By mastering these properties, you can efficiently simplify and solve square root equations.
Simplifying Square Root Expressions
Simplifying square root expressions involves reducing them to their simplest form. Here are the steps and rules to simplify square root expressions effectively:
Basic Rules for Simplifying Square Roots
- Rule 1: \(\sqrt{x} \cdot \sqrt{y} = \sqrt{xy}\)
- Rule 2: \(\frac{\sqrt{x}}{\sqrt{y}} = \sqrt{\frac{x}{y}}\)
- Rule 3: \((\sqrt{x})^2 = x\)
Steps to Simplify Square Root Expressions
- Identify the radical expression and check if it can be simplified.
- Use Rule 1 to combine radicals that are multiplied together.
- Apply Rule 2 for division under the radicals.
- Use Rule 3 to remove radicals by squaring them if necessary.
Examples
Here are some examples to illustrate the simplification process:
| Expression | Simplification |
|---|---|
| \(\sqrt{50}\) | \(\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\) |
| \(\sqrt{72}\) | \(\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}\) |
| \(\frac{\sqrt{18}}{\sqrt{2}}\) | \(\frac{\sqrt{18}}{\sqrt{2}} = \sqrt{\frac{18}{2}} = \sqrt{9} = 3\) |
| \(\sqrt{2} \cdot \sqrt{8}\) | \(\sqrt{2} \cdot \sqrt{8} = \sqrt{2 \cdot 8} = \sqrt{16} = 4\) |
Practice Problems
Try simplifying these square root expressions:
- \(\sqrt{98}\)
- \(\sqrt{75}\)
- \(\sqrt{48} / \sqrt{3}\)
- \(\sqrt{5} \cdot \sqrt{20}\)
Simplifying square root expressions becomes easier with practice. Use these rules and steps to tackle more complex problems effectively.
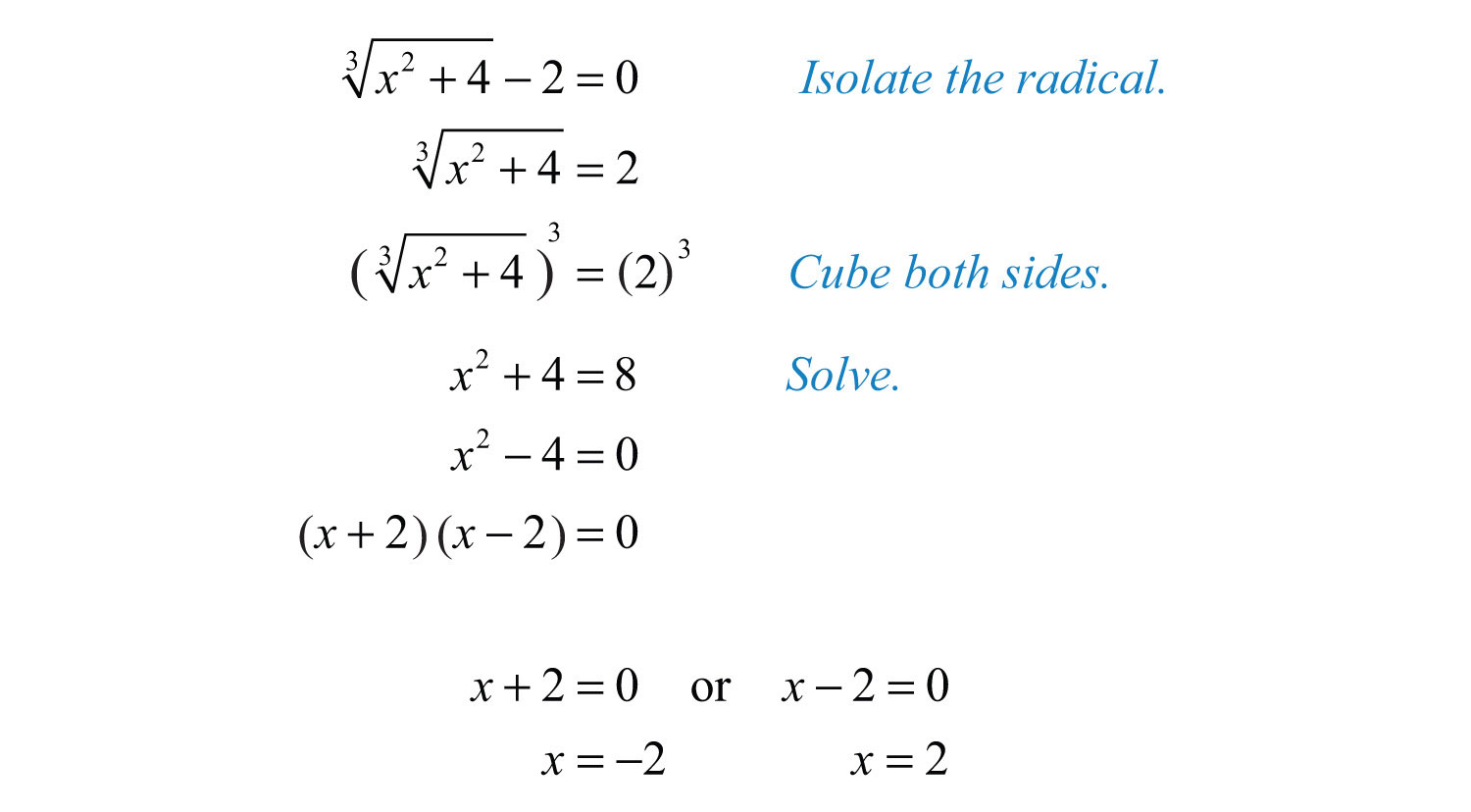
Common Techniques and Methods
Solving square root equations involves several key techniques that can simplify the process. Below, we outline some of the most common methods used by mathematicians and students alike.
1. Isolate the Square Root
To start solving a square root equation, isolate the square root term on one side of the equation. This makes it easier to apply further operations. For example:
\(\sqrt{2x + 9} = 5\)
2. Square Both Sides
Once the square root is isolated, square both sides of the equation to eliminate the square root. This step converts the equation into a simpler form:
\((\sqrt{2x + 9})^2 = 5^2\)
Which simplifies to:
\(2x + 9 = 25\)
3. Solve the Resulting Equation
After squaring both sides, solve the resulting linear or polynomial equation. In our example, subtract 9 from both sides to isolate the term with the variable:
\(2x + 9 - 9 = 25 - 9\)
\(2x = 16\)
Then, divide by 2:
\(x = \frac{16}{2}\)
\(x = 8\)
4. Check for Extraneous Solutions
It's important to check your solutions by substituting them back into the original equation. This ensures that the solutions are valid and not extraneous, which can occur when squaring both sides of an equation.
For \(x = 8\), check:
\(\sqrt{2(8) + 9} = 5\)
\(\sqrt{16 + 9} = 5\)
\(\sqrt{25} = 5\)
This confirms that \(x = 8\) is a valid solution.
5. Using a Calculator
Online square root calculators can be very helpful. These tools allow you to input the equation and solve it quickly. Simply enter the equation in the input field, press the solve button, and the calculator will provide the solution. This is especially useful for complex equations.
Examples of Square Root Equations
Here are a few more examples:
- \(\sqrt{3x + 7} = 4\)
- \(\sqrt{x^2 - 6x + 9} = 3\)
- \(\sqrt{5x - 2} = \sqrt{x + 6}\)
By following these steps and using the right tools, solving square root equations can become a manageable task. Practice with different types of equations to gain confidence and proficiency in this area of mathematics.
Using Online Square Root Calculators
Online square root calculators are powerful tools that can simplify and solve square root equations quickly and accurately. These calculators are user-friendly and offer step-by-step solutions, making them ideal for students and professionals alike. Here's a detailed guide on how to use them effectively:
-
Accessing the Calculator: Open a reliable online square root calculator, such as those available on Mathway or Symbolab.
-
Entering the Expression: Input the square root equation or expression into the calculator. For example, to find the square root of 16, you would enter
\(\sqrt{16}\).If the expression is more complex, such as \(\sqrt{2} + \sqrt{3}\), ensure that you input it accurately to get the correct result.
-
Choosing the Operation: Select the appropriate operation, such as "Calculate the Square Root" or "Simplify the Expression." Most calculators have a dropdown menu for this purpose.
-
Calculating the Result: Click the calculate or solve button. The calculator will process the input and provide the result. For instance, the square root of 16 will yield 4, and the simplified form of \(\sqrt{2} \cdot \sqrt{8}\) will yield 4 as well.
-
Interpreting the Output: The calculator will display the result, often in both exact and decimal forms. For example, \(\sqrt{20}\) might be shown as \(2\sqrt{5}\) and approximately 4.472.
Using these steps, you can solve various square root problems efficiently. Here are some additional tips to maximize the use of online calculators:
- Practice with Different Equations: Experiment with different types of square root equations to become familiar with the calculator's capabilities.
- Use the Step-by-Step Feature: Many calculators, like those on MathCracker, offer detailed step-by-step solutions. This feature helps you understand the process behind the calculation.
- Check Your Work: Use the calculator to verify manual calculations and ensure accuracy.
- Explore Advanced Features: Some calculators offer advanced functionalities, such as solving equations with variables or providing graphical representations.
By following these guidelines, you can effectively use online square root calculators to simplify your mathematical tasks and enhance your problem-solving skills.
Examples of Solved Square Root Equations
Here are a few examples of solved square root equations to help you understand the process and techniques involved in solving these types of problems:
Example 1: Solving a Simple Square Root Equation
Equation: \(\sqrt{x} = 4\)
- Square both sides to eliminate the square root: \((\sqrt{x})^2 = 4^2\)
- Simplify: \(x = 16\)
Example 2: Solving an Equation with a Square Root and a Constant
Equation: \(\sqrt{x+5} = 3\)
- Square both sides to eliminate the square root: \((\sqrt{x+5})^2 = 3^2\)
- Simplify: \(x + 5 = 9\)
- Solve for \(x\): \(x = 9 - 5\)
- Result: \(x = 4\)
Example 3: Solving a More Complex Square Root Equation
Equation: \(\sqrt{2x + 3} = x - 1\)
- Square both sides to eliminate the square root: \((\sqrt{2x + 3})^2 = (x - 1)^2\)
- Simplify: \(2x + 3 = x^2 - 2x + 1\)
- Rearrange the equation to form a quadratic equation: \(x^2 - 4x - 2 = 0\)
- Solve the quadratic equation using the quadratic formula: \(x = \frac{4 \pm \sqrt{(4)^2 - 4 \cdot 1 \cdot (-2)}}{2 \cdot 1}\)
- Simplify the solution: \(x = \frac{4 \pm \sqrt{16 + 8}}{2} = \frac{4 \pm \sqrt{24}}{2} = \frac{4 \pm 2\sqrt{6}}{2} = 2 \pm \sqrt{6}\)
- Check both solutions in the original equation to ensure they are valid.
Example 4: Solving a Square Root Equation with Multiple Square Roots
Equation: \(\sqrt{x+4} + \sqrt{x-1} = 5\)
- Isolate one of the square roots: \(\sqrt{x+4} = 5 - \sqrt{x-1}\)
- Square both sides: \((\sqrt{x+4})^2 = (5 - \sqrt{x-1})^2\)
- Simplify: \(x + 4 = 25 - 10\sqrt{x-1} + x - 1\)
- Combine like terms: \(4 = 24 - 10\sqrt{x-1}\)
- Isolate the remaining square root: \(10\sqrt{x-1} = 20\)
- Solve for \(x\): \(\sqrt{x-1} = 2\), then square both sides: \(x - 1 = 4\), so \(x = 5\)
By following these examples, you can understand the step-by-step process involved in solving different types of square root equations. Practice with similar problems to improve your skills!
Tips for Solving Complex Square Root Problems
Solving complex square root problems can be challenging, but with the right approach, you can simplify and solve them efficiently. Here are some tips to help you tackle these problems:
- Isolate the Square Root: The first step in solving a square root equation is to isolate the square root expression on one side of the equation. This makes it easier to eliminate the square root in the subsequent steps.
- Square Both Sides: Once the square root is isolated, square both sides of the equation to remove the square root. Be cautious when squaring binomials to ensure that all terms are correctly expanded.
- Combine Like Terms: After eliminating the square root, combine like terms and simplify the equation. This often results in a linear or quadratic equation that can be solved using standard algebraic methods.
- Check for Extraneous Solutions: Squaring both sides of an equation can introduce extraneous solutions. Always substitute the solutions back into the original equation to verify their validity.
- Use Rationalizing Techniques: In cases where the square root appears in the denominator, multiply the numerator and denominator by the conjugate of the denominator to rationalize it.
- Utilize Online Calculators: Online tools such as the Symbolab Square Root Calculator and SnapXam Solver can provide step-by-step solutions and help verify your answers.
- Practice Different Methods: Familiarize yourself with various methods like factoring, completing the square, and using the quadratic formula, as they can be useful in different scenarios.
Example Problem:
Solve the equation: \( \sqrt{x + 4} + \sqrt{x - 1} = 5 \)
- Isolate one of the square roots:
\( \sqrt{x + 4} = 5 - \sqrt{x - 1} \)
- Square both sides:
\( (\sqrt{x + 4})^2 = (5 - \sqrt{x - 1})^2 \)
\( x + 4 = 25 - 10\sqrt{x - 1} + (x - 1) \)
- Combine like terms:
\( x + 4 = 24 - 10\sqrt{x - 1} + x \)
\( 4 = 24 - 10\sqrt{x - 1} \)
\( -20 = -10\sqrt{x - 1} \)
\( 2 = \sqrt{x - 1} \)
- Square both sides again:
\( 4 = x - 1 \)
\( x = 5 \)
- Check the solution:
Substitute \( x = 5 \) into the original equation:
\( \sqrt{5 + 4} + \sqrt{5 - 1} = 5 \)
\( 3 + 2 = 5 \), which is true.
The solution to the equation is \( x = 5 \).
By following these steps and tips, you can effectively solve complex square root problems and improve your mathematical skills.

Common Mistakes and How to Avoid Them
Solving square root equations can be challenging, and it's common to make mistakes along the way. Here are some of the most frequent errors and tips on how to avoid them:
- Forgetting to Square Both Sides: When solving an equation involving a square root, it's essential to square both sides of the equation to eliminate the square root. Forgetting this step can lead to incorrect results.
Tip: Always remember to apply the square function to both sides of the equation.
Example:
Given: \( \sqrt{2x+9} = 5 \)
Square both sides:
\( (\sqrt{2x+9})^2 = 5^2 \)
\( 2x + 9 = 25 \)
- Incorrectly Handling Negative Solutions: Square root equations can sometimes yield extraneous solutions. Always check your solutions by substituting them back into the original equation.
Tip: Verify each solution by plugging it back into the original equation to ensure it is valid.
- Not Isolating the Square Root: Before squaring both sides, make sure the square root term is isolated on one side of the equation. Failing to do so can complicate the problem and lead to errors.
Tip: Isolate the square root term before squaring both sides.
Example:
Given: \( \sqrt{x+1} - 3 = 0 \)
Isolate the square root term:
\( \sqrt{x+1} = 3 \)
Square both sides:
\( (\sqrt{x+1})^2 = 3^2 \)
\( x + 1 = 9 \)
\( x = 8 \)
- Forgetting to Simplify: After squaring both sides, ensure you simplify the equation completely. This step is crucial for finding the correct solution.
Tip: Always simplify the equation after squaring both sides.
- Missing Additional Solutions: Some equations can have more than one solution. Ensure you find all possible solutions by considering both positive and negative roots.
Tip: Check for all potential solutions by considering both positive and negative roots, if applicable.
- Ignoring Domain Restrictions: The solutions must satisfy the domain of the original equation, particularly with square roots, where the radicand (the number inside the square root) must be non-negative.
Tip: Consider the domain restrictions of the original equation to ensure the solutions are valid.
Advanced Topics in Square Root Equations
Square root equations can become increasingly complex, involving advanced techniques and concepts. Below are some advanced topics to help deepen your understanding:
- Solving Radical Equations:
Radical equations are equations in which the variable is under a radical, usually a square root. To solve these, follow these steps:
- Isolate the radical expression on one side of the equation.
- Square both sides of the equation to eliminate the radical.
- Solve the resulting polynomial equation.
- Check all potential solutions in the original equation to avoid extraneous solutions.
Example:
\( \sqrt{x + 4} = 5 - \sqrt{x - 1} \)
Square both sides:
\( x + 4 = (5 - \sqrt{x - 1})^2 \)
Expand and simplify:
\( x + 4 = 25 - 10\sqrt{x - 1} + x - 1 \)
Isolate the radical again and square both sides a second time to solve for \( x \).
- Polynomial Division in Radical Equations:
Sometimes, radical equations involve polynomial terms that require division. For instance, consider solving:
\( \sqrt{2x^3 - x^2 + x} = x + 1 \)
Square both sides:
\( 2x^3 - x^2 + x = (x + 1)^2 \)
Expand and simplify to form a polynomial equation. Then use polynomial division to solve for \( x \).
- Systems of Equations with Radicals:
Solving systems of equations where one or both equations contain radicals can be challenging. The key steps involve:
- Isolating the radical in one of the equations.
- Squaring both sides to eliminate the radical.
- Substituting into the other equation to solve the system.
- Checking all potential solutions in the original system to ensure they are valid.
Example:
Solve the system:
\( \sqrt{y + 2} = x + 3 \)
\( y = x^2 - 4 \)
- Exponential and Logarithmic Functions with Radicals:
Combining exponential and logarithmic functions with radicals requires a strong grasp of algebraic manipulation and properties of exponents and logarithms.
Example:
Solve for \( x \):
\( \sqrt{e^{2x} + 1} = 3 \)
Square both sides to remove the radical and solve the resulting exponential equation.
- Complex Numbers and Radicals:
When dealing with square roots of negative numbers, complex numbers come into play. Understanding how to solve equations involving \( i = \sqrt{-1} \) is crucial for advanced mathematics.
Example:
Solve for \( x \):
\( \sqrt{x^2 + 1} = 2i \)
Square both sides and solve for \( x \).
Practice Problems and Solutions
Practicing square root equations is essential for mastering the concept. Below are some example problems along with detailed solutions to help you understand the process step by step.
Example 1: Solve \( \sqrt{x+4} = 5 - \sqrt{x-1} \)
- Start with the given equation:
\( \sqrt{x+4} = 5 - \sqrt{x-1} \)
- Isolate one of the square root terms by squaring both sides:
\( (\sqrt{x+4})^2 = (5 - \sqrt{x-1})^2 \)
\( x + 4 = 25 - 10\sqrt{x-1} + (x-1) \)
- Simplify the equation:
\( x + 4 = 25 + x - 1 - 10\sqrt{x-1} \)
\( x + 4 = 24 + x - 10\sqrt{x-1} \)
- Isolate the square root term:
\( 10\sqrt{x-1} = 24 + x - x - 4 \)
\( 10\sqrt{x-1} = 20 \)
- Square both sides again to remove the square root:
\( (10\sqrt{x-1})^2 = 20^2 \)
\( 100(x-1) = 400 \)
- Solve for \( x \):
\( 100x - 100 = 400 \)
\( 100x = 500 \)
\( x = 5 \)
Example 2: Solve \( \sqrt{x-2} = 5 \)
- Start with the given equation:
\( \sqrt{x-2} = 5 \)
- Square both sides to eliminate the square root:
\( (\sqrt{x-2})^2 = 5^2 \)
\( x - 2 = 25 \)
- Solve for \( x \):
\( x = 27 \)
Example 3: Solve \( \sqrt{2x+7} = 5 \)
- Start with the given equation:
\( \sqrt{2x+7} = 5 \)
- Square both sides to eliminate the square root:
\( (\sqrt{2x+7})^2 = 5^2 \)
\( 2x + 7 = 25 \)
- Solve for \( x \):
\( 2x = 18 \)
\( x = 9 \)
Example 4: Solve \( \sqrt{x+2} + x = 10 \)
- Start with the given equation:
\( \sqrt{x+2} + x = 10 \)
- Isolate the square root term:
\( \sqrt{x+2} = 10 - x \)
- Square both sides:
\( (\sqrt{x+2})^2 = (10 - x)^2 \)
\( x + 2 = 100 - 20x + x^2 \)
- Rearrange the equation into standard form:
\( x^2 - 21x + 98 = 0 \)
- Solve the quadratic equation using the quadratic formula:
\( x = \frac{21 \pm \sqrt{21^2 - 4 \cdot 1 \cdot 98}}{2 \cdot 1} \)
\( x = \frac{21 \pm \sqrt{441 - 392}}{2} \)
\( x = \frac{21 \pm \sqrt{49}}{2} \)
\( x = \frac{21 \pm 7}{2} \)
\( x = 14 \text{ or } x = 7 \)
These examples should provide a clear understanding of how to approach and solve different types of square root equations. Practice with more problems to enhance your skills!
Additional Resources and References
Here are some valuable resources and references for solving square root equations. These tools and guides can help enhance your understanding and proficiency in working with square roots.
-
CalculatorSoup - Square Root Calculator
This online calculator helps you find the principal square root and roots of real numbers. It can handle both positive and negative inputs, providing results for both perfect and non-perfect squares. The tool also offers a fractional exponent calculator for more complex calculations.
Visit the calculator here:
-
SnapXam - Equations with Square Roots Calculator
SnapXam provides a detailed step-by-step calculator for solving equations with square roots. It is particularly useful for practice and learning, as it breaks down the solutions into manageable steps and explains each one thoroughly.
Explore the tool here:
-
Mathway - Algebra Calculator
Mathway offers a versatile algebra calculator that can solve a variety of equations, including those involving square roots. It provides instant step-by-step solutions, making it an excellent resource for students and anyone needing quick assistance with algebra problems.
Check out Mathway here:
-
WolframAlpha - Square Root Solver
WolframAlpha is a powerful computational engine that can solve square root equations and provide detailed explanations. It is a great tool for deeper exploration and understanding of mathematical concepts.
Use WolframAlpha here:
-
Khan Academy - Square Roots and Radicals
Khan Academy offers comprehensive tutorials and practice exercises on square roots and radicals. The lessons are designed to build a strong foundational understanding and provide practice problems to reinforce learning.
Visit Khan Academy here:
These resources should provide you with the tools and knowledge needed to master solving square root equations. Happy learning!
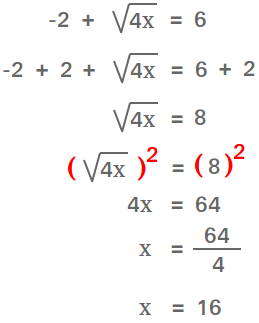
Hướng Dẫn Sử Dụng Máy Tính ClassWiz - Đại Số 4-1 Đơn Giản Hóa Biểu Thức Căn