Topic simplify square root of negative 72: Learn how to simplify the square root of negative 72 with our step-by-step guide. Discover the principles behind complex numbers and imaginary units, making it easy to understand and apply these concepts. Perfect for students and math enthusiasts looking to enhance their skills.
Table of Content
- Simplifying the Square Root of Negative Numbers
- Introduction to Square Roots
- Understanding Negative Square Roots
- Complex Numbers and Imaginary Units
- Simplifying the Square Root of Negative Numbers
- Step-by-Step Process to Simplify √-72
- Examples of Simplifying Negative Square Roots
- Applications of Complex Numbers
- Practice Problems
- Common Mistakes and How to Avoid Them
- Conclusion and Further Learning
- YOUTUBE:
Simplifying the Square Root of Negative Numbers
When simplifying the square root of a negative number, we use the concept of imaginary numbers. The imaginary unit, denoted as \( i \), is defined by the property \( i^2 = -1 \). This allows us to express the square root of any negative number in terms of \( i \).
Example: Simplifying \( \sqrt{-72} \)
To simplify \( \sqrt{-72} \), follow these steps:
- Express the negative number as a product of -1 and a positive number:
\[
\sqrt{-72} = \sqrt{-1 \times 72}
\] - Use the property of square roots to separate the factors:
\[
\sqrt{-1 \times 72} = \sqrt{-1} \times \sqrt{72}
\] - Replace \( \sqrt{-1} \) with \( i \):
\[
\sqrt{-1} = i
\] - Identify the square root of 72. Factor 72 into its prime factors:
\[
72 = 2^3 \times 3^2
\] - Simplify \( \sqrt{72} \):
\[
\sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{2^3} \times \sqrt{3^2} = 2 \times \sqrt{2} \times 3 = 6\sqrt{2}
\] - Combine the results:
\[
\sqrt{-72} = i \times 6\sqrt{2} = 6i\sqrt{2}
\]
Thus, the simplified form of \( \sqrt{-72} \) is \( 6i\sqrt{2} \).

READ MORE:
Introduction to Square Roots
Square roots are fundamental in mathematics, representing a number that, when multiplied by itself, results in the original number. For example, the square root of 9 is 3 because 3 × 3 = 9. Understanding how to simplify square roots is crucial for solving various mathematical problems efficiently.
When dealing with square roots, especially of negative numbers, the concept of imaginary numbers becomes essential. The square root of a negative number involves the imaginary unit 'i', where i is defined as √(-1). Thus, the square root of -72 can be expressed as 6i√2.
To simplify the square root of any number, follow these steps:
- Factor the number into its prime factors.
- Group the factors into pairs.
- Bring one factor out of the square root for each pair.
- Multiply the factors outside the square root.
Here's a detailed example to illustrate the process:
| Step | Process | Result |
|---|---|---|
| 1 | Start with the number 72 | 72 |
| 2 | Factor into primes: 72 = 2 × 2 × 2 × 3 × 3 | 2 × 2 × 2 × 3 × 3 |
| 3 | Group pairs: (2 × 2) and (3 × 3) | (2 × 2) and (3 × 3) |
| 4 | Take one factor out from each pair: 2 and 3 | 2 and 3 |
| 5 | Multiply outside factors: 2 × 3 | 6 |
| 6 | Combine with remaining factor inside the square root | 6√2 |
Applying the same principles to the square root of -72 involves the additional step of incorporating the imaginary unit 'i':
- Factor -72 as -1 × 72.
- Recognize √(-1) as 'i'.
- Apply the simplification process to 72 as shown above.
- Combine results: √(-72) = √(-1 × 72) = i√72 = i × 6√2 = 6i√2.
In summary, simplifying square roots, including those of negative numbers, involves understanding prime factorization, grouping, and the role of imaginary numbers. Mastery of these techniques will greatly enhance your mathematical problem-solving skills.
Understanding Negative Square Roots
Negative square roots can be a tricky concept in mathematics because they involve imaginary numbers. When we take the square root of a negative number, we are dealing with imaginary numbers, denoted by the symbol \(i\), where \(i = \sqrt{-1}\).
For example, to simplify the square root of -72, we follow these steps:
- Rewrite -72 as a product of -1 and a positive number: \(-72 = -1 \times 72\).
- Express the square root of -72 as the product of the square roots: \(\sqrt{-72} = \sqrt{-1 \times 72}\).
- Separate the square roots: \(\sqrt{-72} = \sqrt{-1} \times \sqrt{72}\).
- Replace \(\sqrt{-1}\) with \(i\): \(\sqrt{-72} = i \times \sqrt{72}\).
- Simplify \(\sqrt{72}\) by breaking it down into prime factors: \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\).
- Combine the results: \(\sqrt{-72} = 6i\sqrt{2}\).
Thus, the simplified form of \(\sqrt{-72}\) is \(6i\sqrt{2}\).
This process highlights how imaginary numbers are used to simplify the square roots of negative numbers, making complex problems more manageable.
Complex Numbers and Imaginary Units
Understanding complex numbers and imaginary units is essential for simplifying square roots of negative numbers. When dealing with the square root of a negative number, such as -72, the concept of imaginary units comes into play. The imaginary unit, denoted as \(i\), is defined as \(i = \sqrt{-1}\).
Using this definition, any negative square root can be expressed in terms of \(i\). For instance, the square root of -72 can be simplified as follows:
- Identify the negative number inside the square root: \(\sqrt{-72}\).
- Separate the negative sign and the positive part: \(\sqrt{-1 \times 72}\).
- Apply the property of square roots: \(\sqrt{-1} \times \sqrt{72}\).
- Replace \(\sqrt{-1}\) with \(i\): \(i \times \sqrt{72}\).
Next, simplify \(\sqrt{72}\) by finding its prime factors:
- Prime factorization of 72: \(72 = 2^3 \times 3^2\).
- Apply the square root to each factor: \(\sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{2^2 \times 2 \times 3^2} = 6\sqrt{2}\).
Combining these results, we get:
\(\sqrt{-72} = i \times 6\sqrt{2} = 6i\sqrt{2}\).
This demonstrates how complex numbers and imaginary units simplify the process of dealing with square roots of negative numbers.
Simplifying the Square Root of Negative Numbers
When dealing with the square root of negative numbers, we enter the realm of complex numbers. A complex number has a real part and an imaginary part, typically expressed in the form \(a + bi\), where \(i\) is the imaginary unit defined by \(i = \sqrt{-1}\).
To simplify the square root of a negative number, we follow these steps:
-
Identify the negative number under the square root. For example, \(\sqrt{-72}\).
-
Express the negative number as the product of a positive number and \(-1\). For instance, \(-72\) can be written as \(72 \times (-1)\).
-
Use the property of square roots that \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\). So, \(\sqrt{-72} = \sqrt{72 \times (-1)} = \sqrt{72} \times \sqrt{-1}\).
-
Recall that \(\sqrt{-1} = i\). Therefore, \(\sqrt{-72} = \sqrt{72} \times i\).
-
Simplify the square root of the positive number. In this case, \(72\) can be factored into \(36 \times 2\), so \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\).
-
Combine the results to obtain the simplified form: \(\sqrt{-72} = 6\sqrt{2} \times i = 6i\sqrt{2}\).
Therefore, the square root of \(-72\) simplifies to \(6i\sqrt{2}\). Understanding this process is crucial for working with complex numbers and solving equations involving negative square roots.
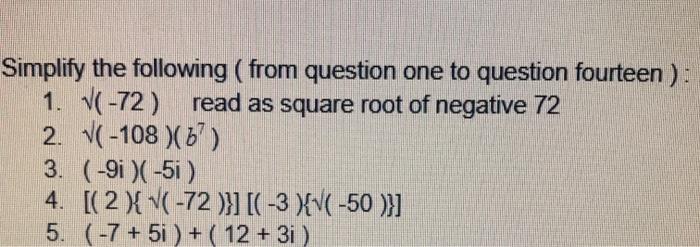
Step-by-Step Process to Simplify √-72
To simplify the square root of -72, follow these steps:
- Identify the Negative Sign:
The square root of a negative number involves the imaginary unit i, where i is defined as √-1.
- Rewrite the Expression:
Express √-72 as √-1 × √72, which can be written as i√72.
- Prime Factorization:
Factor 72 into its prime components: 72 = 2 × 2 × 2 × 3 × 3.
- Group the Factors:
Group the factors into pairs: 72 = (2 × 2) × (3 × 3) × 2. This can be written as 22 × 32 × 2.
- Take the Square Roots:
Simplify the pairs: √(22) = 2 and √(32) = 3.
- Combine the Results:
Combine the simplified terms: 2 × 3 = 6, and multiply by the remaining √2: 6√2.
- Include the Imaginary Unit:
Combine with the imaginary unit i: i × 6√2.
- Final Simplified Form:
The simplified form of √-72 is 6i√2.
Examples of Simplifying Negative Square Roots
To simplify the square root of a negative number, we use the imaginary unit \(i\), where \(i = \sqrt{-1}\). Here are a few examples:
-
Example 1: Simplifying \(\sqrt{-72}\)
- Express the negative inside the square root as \(\sqrt{72} \cdot \sqrt{-1}\).
- Replace \(\sqrt{-1}\) with \(i\): \(\sqrt{72} \cdot i\).
- Simplify \(\sqrt{72}\) by factoring: \(\sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}\).
- Combine the results: \(6\sqrt{2} \cdot i\) or \(6i\sqrt{2}\).
-
Example 2: Simplifying \(\sqrt{-50}\)
- Express the negative inside the square root as \(\sqrt{50} \cdot \sqrt{-1}\).
- Replace \(\sqrt{-1}\) with \(i\): \(\sqrt{50} \cdot i\).
- Simplify \(\sqrt{50}\) by factoring: \(\sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\).
- Combine the results: \(5\sqrt{2} \cdot i\) or \(5i\sqrt{2}\).
-
Example 3: Simplifying \(\sqrt{-32}\)
- Express the negative inside the square root as \(\sqrt{32} \cdot \sqrt{-1}\).
- Replace \(\sqrt{-1}\) with \(i\): \(\sqrt{32} \cdot i\).
- Simplify \(\sqrt{32}\) by factoring: \(\sqrt{16 \cdot 2} = \sqrt{16} \cdot \sqrt{2} = 4\sqrt{2}\).
- Combine the results: \(4\sqrt{2} \cdot i\) or \(4i\sqrt{2}\).
Applications of Complex Numbers
Complex numbers, which are in the form \(a + bi\) where \(a\) and \(b\) are real numbers and \(i\) is the imaginary unit (\(i^2 = -1\)), have a wide range of applications in various fields. Here are some notable applications:
-
Electrical Engineering
In electrical engineering, complex numbers are used to represent impedance in circuits. Impedance combines resistance, inductance, and capacitance, and is represented as \(Z = R + jX\), where \(R\) is resistance and \(X\) is reactance.
-
Control Theory
Complex numbers are essential in control theory for analyzing and designing control systems. Techniques such as the root locus method and frequency domain analysis heavily rely on complex numbers.
-
Quantum Mechanics
In quantum mechanics, the wave function, which describes the state of a quantum system, is typically a complex-valued function. The Schrödinger equation, fundamental to quantum mechanics, involves complex numbers.
-
Signal Processing
Complex numbers are used in signal processing to represent signals in the frequency domain. The Fourier transform, which decomposes signals into their frequency components, uses complex numbers.
-
Computer Graphics
In computer graphics, complex numbers are used for various transformations and simulations. They are particularly useful in generating fractals, such as the Mandelbrot set.
-
Fluid Mechanics
In fluid mechanics, complex numbers are used to describe potential flow in two dimensions, aiding in calculations of forces and moments of inertia in various applications like aerodynamics and hydrodynamics.
-
Electromagnetism
Complex numbers simplify the representation of electromagnetic fields by combining the electric and magnetic components into a single complex quantity.
-
Relativity
In the theories of relativity, some equations become simpler when time is treated as an imaginary quantity, facilitating the mathematical handling of space-time concepts.
These examples illustrate the critical role of complex numbers in advancing our understanding and capabilities across various scientific and engineering disciplines.
Practice Problems
Here are some practice problems to help you understand how to simplify the square roots of negative numbers and work with complex numbers.
- Simplify the following square roots of negative numbers:
- √-8
- √-18
- √-50
- √-100
Follow these steps to simplify each square root:
- Identify the positive part of the number inside the square root.
- Factor the number into its prime factors, if possible.
- Extract the square root of each factor, using the imaginary unit \(i\) for the negative part.
Let's work through the first example together:
- Simplify \( \sqrt{-8} \)
- Rewrite as \( \sqrt{8} \cdot \sqrt{-1} \).
- The square root of -1 is \(i\), so this becomes \( \sqrt{8} \cdot i \).
- Factor 8 into \(4 \cdot 2\), so \( \sqrt{8} = \sqrt{4 \cdot 2} = \sqrt{4} \cdot \sqrt{2} = 2\sqrt{2} \).
- Combine to get the final simplified form: \( 2\sqrt{2} \cdot i = 2i\sqrt{2} \).
Now, try to simplify the rest on your own. Here are the steps you need to take:
- For √-18:
- Rewrite as \( \sqrt{18} \cdot \sqrt{-1} \).
- Factor 18 into \(9 \cdot 2\), so \( \sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2} \).
- Combine to get the final simplified form: \( 3\sqrt{2} \cdot i = 3i\sqrt{2} \).
- For √-50:
- Rewrite as \( \sqrt{50} \cdot \sqrt{-1} \).
- Factor 50 into \(25 \cdot 2\), so \( \sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2} \).
- Combine to get the final simplified form: \( 5\sqrt{2} \cdot i = 5i\sqrt{2} \).
- For √-100:
- Rewrite as \( \sqrt{100} \cdot \sqrt{-1} \).
- The square root of 100 is 10, so \( \sqrt{100} = 10 \).
- Combine to get the final simplified form: \( 10 \cdot i = 10i \).
Check your answers using the method described above. Practicing these problems will help you become more comfortable with simplifying square roots of negative numbers and working with complex numbers.

Common Mistakes and How to Avoid Them
Simplifying the square root of negative numbers can be tricky. Here are some common mistakes to watch out for and tips to avoid them:
-
Mistake 1: Ignoring the Imaginary Unit
When simplifying the square root of a negative number, it's crucial to include the imaginary unit \(i\). For example, \(\sqrt{-72}\) should be simplified to \(\sqrt{72} \cdot i\).
Avoid this mistake: Always factor out \(-1\) and use \(i\) when dealing with negative radicands.
-
Mistake 2: Incorrect Simplification of Radicals
Another common mistake is not correctly simplifying the square root of the positive part of the number. For example, \(\sqrt{72}\) should be simplified to \(6\sqrt{2}\).
Avoid this mistake: Break down the number under the square root into its prime factors and simplify.
-
Mistake 3: Incorrect Multiplication of Imaginary Units
When simplifying expressions involving \(i\), ensure proper multiplication rules are followed. Remember that \(i^2 = -1\).
Avoid this mistake: Carefully multiply and simplify terms involving \(i\).
-
Mistake 4: Overcomplicating the Expression
Sometimes, students add unnecessary steps or misapply properties of radicals, leading to more complex expressions.
Avoid this mistake: Stick to the fundamental properties of square roots and imaginary numbers, and simplify step-by-step.
-
Mistake 5: Misunderstanding the Principal Root
It's important to recognize that the principal root of a number is always the positive root. For example, the principal root of 4 is 2, not -2.
Avoid this mistake: Remember that the principal square root is always positive.
Conclusion and Further Learning
Understanding how to simplify the square root of negative numbers, such as \(\sqrt{-72}\), opens the door to a deeper appreciation of complex numbers and their applications. By following the step-by-step process to convert a negative square root into a form involving the imaginary unit \(i\), you can simplify expressions involving complex numbers with confidence.
In this guide, we covered the basics of square roots, the significance of negative square roots, and the role of complex numbers. We specifically simplified \(\sqrt{-72}\) by breaking it down into manageable parts, ultimately expressing it as \(6i\sqrt{2}\).
As you continue your mathematical journey, keep in mind the following key points:
- Always remember to separate the negative sign when dealing with square roots of negative numbers, using \(i\) to represent \(\sqrt{-1}\).
- Practice simplifying the square roots of various negative numbers to become more familiar with the process.
- Use the quotient property and other simplification techniques for complex fractions and radicals.
For further learning, consider exploring the following topics:
- Advanced operations with complex numbers, including addition, subtraction, multiplication, and division.
- The geometric representation of complex numbers on the complex plane.
- Applications of complex numbers in engineering, physics, and other fields.
- Polynomials and complex roots, including the Fundamental Theorem of Algebra.
By building on the foundational skills you've developed here, you can advance to more sophisticated mathematical concepts and their real-world applications.
Happy learning!
Đơn giản hóa căn bậc hai: -sqrt(72)
READ MORE:
Đơn Giản Hóa Căn Bậc Hai của Số Âm | Thủ Thuật Toán Học











