Topic simplify square root cal: Learn how to simplify square roots with ease using our comprehensive guide. Whether you're tackling basic or advanced expressions, our step-by-step instructions and examples will help you master the process. Discover tips, tricks, and calculators to simplify any square root quickly and accurately. Perfect for students, teachers, and math enthusiasts looking to enhance their skills.
Table of Content
- Simplifying Square Roots
- Introduction to Square Roots
- Understanding the Square Root Symbol
- Steps to Simplify Square Roots
- Examples of Simplifying Square Roots
- Properties of Square Roots
- Special Cases in Simplifying Square Roots
- Simplifying Square Roots of Fractions
- Simplifying Radicals
- Common Mistakes and How to Avoid Them
- Using Square Root Calculators
- Practice Problems and Solutions
- Additional Resources
- YOUTUBE: Hãy xem video này để học cách giản đơn các căn bậc hai bằng cây nhân bội trong đại số. Phần 1 của loạt video giải thích chi tiết về biểu thức căn bậc hai và cách thực hiện quy trình giản đơn.
Simplifying Square Roots
To simplify a square root, the number inside the square root should be made as small as possible while remaining a whole number. This can be done using the property of square roots: when \(a\) and \(b\) are non-negative, \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\).
Examples:
-
Example 1: Simplify \(\sqrt{12}\)
12 can be factored into 4 and 3:
\(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\)
-
Example 2: Simplify \(\sqrt{45}\)
45 can be factored into 9 and 5:
\(\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}\)
-
Example 3: Simplify \(\sqrt{8}\)
8 can be factored into 4 and 2:
\(\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2}\)
-
Example 4: Simplify \(\sqrt{18}\)
18 can be factored into 9 and 2:
\(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)
Combining Square Roots:
Square roots can be combined and simplified further by factoring and using the property \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\).
-
Example: Simplify \(\sqrt{6} \times \sqrt{15}\)
First, combine the two numbers:
\(\sqrt{6} \times \sqrt{15} = \sqrt{6 \times 15} = \sqrt{90}\)
Next, factor 90 into 9 and 10:
\(\sqrt{90} = \sqrt{9 \times 10} = \sqrt{9} \times \sqrt{10} = 3\sqrt{10}\)
Fractions:
There is a similar rule for simplifying square roots of fractions:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
-
Example: Simplify \(\frac{\sqrt{30}}{\sqrt{10}}\)
\(\frac{\sqrt{30}}{\sqrt{10}} = \sqrt{\frac{30}{10}} = \sqrt{3}\)
Complex Examples:
-
Example: Simplify \(2\sqrt{12} + 9\sqrt{3}\)
First, simplify \(2\sqrt{12}\):
\(2\sqrt{12} = 2 \times 2\sqrt{3} = 4\sqrt{3}\)
Now both terms have \(\sqrt{3}\), so they can be added:
\(4\sqrt{3} + 9\sqrt{3} = (4 + 9)\sqrt{3} = 13\sqrt{3}\)
Surds:
A root that cannot be simplified further is called a surd. For example, \(\sqrt{3}\) is a surd because it cannot be simplified further, but \(\sqrt{4} = 2\) is not a surd.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, representing a number that, when multiplied by itself, gives the original number. The symbol for the square root is √, and it is used to denote the principal square root, which is always a non-negative value. For example, the square root of 25 is 5 because 5 × 5 = 25.
Understanding square roots is essential for solving various algebraic problems, and they play a crucial role in fields ranging from engineering to finance. Here are the basic concepts related to square roots:
- Principal Square Root: The non-negative square root of a number. For example, the principal square root of 16 is 4.
- Negative Square Roots: Every positive number also has a negative square root. For instance, the square roots of 16 are 4 and -4, because both 4 × 4 and -4 × -4 equal 16.
- Perfect Squares: Numbers that have integer square roots. Examples include 1, 4, 9, 16, and 25.
- Non-Perfect Squares: Numbers that do not have integer square roots. Their square roots are irrational numbers. For example, √2 is approximately 1.414, and it cannot be expressed as a precise fraction.
Here is a step-by-step process to find the square root of a number:
- Identify if the number is a perfect square: Check if the number can be expressed as the product of an integer with itself.
- Use prime factorization: If the number is not a perfect square, factorize it into prime numbers. Pair the prime factors to simplify the square root.
- Approximate for non-perfect squares: If the number is not a perfect square and cannot be simplified further, use approximation methods or a calculator to find the square root.
For example:
- Simplifying √18: Factorize 18 into 2 × 3 × 3. Pair the 3s to get 3√2. Therefore, √18 simplifies to 3√2.
- Calculating √50: Factorize 50 into 2 × 5 × 5. Pair the 5s to get 5√2. Therefore, √50 simplifies to 5√2.
Understanding these steps and concepts will help you simplify square roots and solve related mathematical problems efficiently.
Understanding the Square Root Symbol
The square root symbol, denoted as √, represents a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 × 3 = 9.
Here are some key points to understand about the square root symbol:
- The expression √a means "the square root of a."
- √a is only defined for non-negative values of a.
- Square roots can be simplified by factoring out perfect squares.
Let’s explore how to simplify square roots:
- Identify Perfect Squares: Find the largest perfect square factor of the number under the square root. For instance, for √18, the perfect square factor is 9 (since 18 = 9 × 2).
- Rewrite the Expression: Break down the square root into the product of square roots. For √18, this would be √(9 × 2).
- Simplify: Take the square root of the perfect square factor and multiply it by the square root of the remaining factor. For √(9 × 2), this becomes √9 × √2, which simplifies to 3√2.
Here are some examples:
| Expression | Simplified Form |
|---|---|
| √12 | 2√3 (since 12 = 4 × 3 and √4 = 2) |
| √45 | 3√5 (since 45 = 9 × 5 and √9 = 3) |
| √8 | 2√2 (since 8 = 4 × 2 and √4 = 2) |
By understanding and applying these steps, you can simplify square roots effectively, making complex calculations more manageable.
Steps to Simplify Square Roots
Simplifying square roots involves reducing the expression inside the radical to its simplest form. Here are the steps to simplify square roots:
- Identify Perfect Squares: Look for perfect square factors of the number under the square root.
- Factor the Number: Break down the number under the square root into its prime factors.
- Apply the Square Root Rule: Use the rule \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) to separate the square root into simpler parts.
- Simplify: Take the square root of the perfect square factors.
- Multiply: Multiply the simplified square roots together.
Here are some examples to illustrate these steps:
Example 1: Simplify \( \sqrt{12} \)
- Factor 12: \( 12 = 4 \times 3 \)
- Separate the square roots: \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \cdot \sqrt{3} \)
- Simplify: \( \sqrt{4} = 2 \)
- Result: \( \sqrt{12} = 2\sqrt{3} \)
Example 2: Simplify \( \sqrt{45} \)
- Factor 45: \( 45 = 9 \times 5 \)
- Separate the square roots: \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \cdot \sqrt{5} \)
- Simplify: \( \sqrt{9} = 3 \)
- Result: \( \sqrt{45} = 3\sqrt{5} \)
Example 3: Simplify \( \sqrt{18} \)
- Factor 18: \( 18 = 9 \times 2 \)
- Separate the square roots: \( \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \cdot \sqrt{2} \)
- Simplify: \( \sqrt{9} = 3 \)
- Result: \( \sqrt{18} = 3\sqrt{2} \)
By following these steps, you can simplify any square root expression effectively.
Examples of Simplifying Square Roots
Here are several examples to help you understand the process of simplifying square roots:
Example 1: Simplify √12
- Identify the factors of 12 that include a perfect square: \(12 = 4 \times 3\)
- Apply the product property of square roots: \(\sqrt{12} = \sqrt{4 \times 3}\)
- Simplify using the known square root: \(\sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\)
Example 2: Simplify √45
- Identify the factors of 45 that include a perfect square: \(45 = 9 \times 5\)
- Apply the product property of square roots: \(\sqrt{45} = \sqrt{9 \times 5}\)
- Simplify using the known square root: \(\sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}\)
Example 3: Simplify √72
- Identify the factors of 72 that include a perfect square: \(72 = 36 \times 2\)
- Apply the product property of square roots: \(\sqrt{72} = \sqrt{36 \times 2}\)
- Simplify using the known square root: \(\sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\)
Example 4: Simplify √50
- Identify the factors of 50 that include a perfect square: \(50 = 25 \times 2\)
- Apply the product property of square roots: \(\sqrt{50} = \sqrt{25 \times 2}\)
- Simplify using the known square root: \(\sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\)
Example 5: Simplify √18
- Identify the factors of 18 that include a perfect square: \(18 = 9 \times 2\)
- Apply the product property of square roots: \(\sqrt{18} = \sqrt{9 \times 2}\)
- Simplify using the known square root: \(\sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\)
Example 6: Simplify √98
- Identify the factors of 98 that include a perfect square: \(98 = 49 \times 2\)
- Apply the product property of square roots: \(\sqrt{98} = \sqrt{49 \times 2}\)
- Simplify using the known square root: \(\sqrt{49 \times 2} = \sqrt{49} \times \sqrt{2} = 7\sqrt{2}\)
Practice Problems
- Simplify \(\sqrt{80}\)
- Simplify \(\sqrt{125}\)
- Simplify \(\sqrt{32}\)
- Simplify \(\sqrt{200}\)
Try solving these practice problems to reinforce your understanding of simplifying square roots.
Properties of Square Roots
Understanding the properties of square roots is essential for simplifying expressions and solving equations. Here are the key properties:
-
Product Property:
If two or more numbers are multiplied inside a square root, you can take the square root once and multiply the numbers inside:
\(\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}\)
-
Quotient Property:
If two numbers are divided inside a square root, you can take the square root once and divide the numbers inside:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
-
Power Property:
The square root of a number can be expressed as an exponent of 1/2:
\(\sqrt{a} = a^{1/2}\)
-
Addition and Subtraction:
Square roots can be added or subtracted only if they have the same radicand (the number inside the square root):
\(a\sqrt{b} + c\sqrt{b} = (a+c)\sqrt{b}\)
-
Even and Odd Properties:
The square root of an even perfect square is even, and the square root of an odd perfect square is odd:
- \(\sqrt{64} = 8\)
- \(\sqrt{81} = 9\)
-
Perfect Squares:
A number with a last digit of 0, 1, 4, 5, 6, or 9 can be a perfect square, and its square root will be an integer:
- \(\sqrt{100} = 10\)
- \(\sqrt{121} = 11\)
-
Negative Numbers:
The square root of a negative number is imaginary, represented as \(i\sqrt{a}\) where \(i\) is the imaginary unit:
\(\sqrt{-a} = i\sqrt{a}\)
-
Digit Patterns:
If a number ends with an even number of zeros, its square root will be an integer:
- \(\sqrt{10000} = 100\)
-
Sum of Odd Numbers:
The square of a natural number is equal to the sum of the first \(n\) odd numbers:
\(n^2 = 1 + 3 + 5 + ... + (2n-1)\)
Special Cases in Simplifying Square Roots
While simplifying square roots, there are several special cases that can arise. Understanding these can help in quickly and accurately simplifying square roots in various scenarios.
-
Perfect Squares:
When the number under the square root is a perfect square, the square root is an integer. For example:
- √16 = 4
- √25 = 5
-
Square Roots of Fractions:
The square root of a fraction can be found by taking the square root of the numerator and the denominator separately. For example:
- √(4/9) = √4 / √9 = 2/3
- √(1/16) = √1 / √16 = 1/4
-
Multiplication Inside the Radical:
When multiplying numbers inside a square root, you can multiply them together and then take the square root. For example:
- √(4 * 9) = √36 = 6
- √(2 * 8) = √16 = 4
-
Addition and Subtraction Inside the Radical:
Square roots involving addition or subtraction inside the radical do not simplify in a straightforward manner. For example:
- √(4 + 9) ≠ √4 + √9
- Instead, √(4 + 9) = √13
-
Combining Like Radicals:
Similar to combining like terms in algebra, you can add or subtract like radicals. For example:
- 2√3 + 3√3 = 5√3
- 5√2 - 2√2 = 3√2
-
Simplifying Radicals with Variables:
When simplifying radicals that include variables, apply the same principles. For example:
- √(x^2) = x
- √(9y^2) = 3y
-
Negative Radicands:
Square roots of negative numbers are not real numbers. These are represented using the imaginary unit i. For example:
- √(-1) = i
- √(-9) = 3i
Simplifying Square Roots of Fractions
Simplifying the square root of a fraction involves breaking down the fraction into its numerator and denominator, simplifying each part, and then combining them back together. Here is a step-by-step guide:
-
Separate the Fraction:
Given a fraction inside a square root, separate it into the square root of the numerator and the square root of the denominator.
For example:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\] -
Simplify the Square Roots:
Check if the numerator and the denominator can be simplified. Look for perfect squares that can be factored out.
Example:
\[
\sqrt{\frac{50}{18}} = \frac{\sqrt{50}}{\sqrt{18}} = \frac{\sqrt{25 \times 2}}{\sqrt{9 \times 2}} = \frac{5\sqrt{2}}{3\sqrt{2}}
\] -
Rationalize the Denominator:
If the denominator contains a square root, rationalize it by multiplying the numerator and the denominator by the square root present in the denominator.
Example:
\[
\frac{5\sqrt{2}}{3\sqrt{2}} = \frac{5\sqrt{2} \times \sqrt{2}}{3\sqrt{2} \times \sqrt{2}} = \frac{5 \times 2}{3 \times 2} = \frac{10}{6} = \frac{5}{3}
\] -
Reduce the Fraction:
After rationalizing, reduce the fraction to its simplest form if possible.
Example:
\[
\sqrt{\frac{30}{32}} = \frac{\sqrt{30}}{\sqrt{32}} = \frac{\sqrt{2 \times 15}}{\sqrt{2 \times 16}} = \frac{\sqrt{2} \times \sqrt{15}}{4 \times \sqrt{2}} = \frac{\sqrt{15}}{4}
\]
Here are some additional examples to practice:
- Simplify: \[ \sqrt{\frac{8}{5}} = \frac{2\sqrt{10}}{5} \]
- Simplify: \[ \frac{2}{\sqrt{12}} = \frac{2\sqrt{12}}{12} = \frac{\sqrt{12}}{6} = \frac{2\sqrt{3}}{6} = \frac{\sqrt{3}}{3} \]
Simplifying Radicals
Simplifying radicals involves breaking down the radicand (the number inside the radical symbol) into its prime factors and then applying the properties of square roots. Here are the steps to simplify radicals:
-
Find the largest perfect square factor: Identify the largest perfect square that divides the radicand. This will simplify the process and reduce the number of steps.
For example, to simplify \( \sqrt{72} \):
- The largest perfect square factor of 72 is 36.
- Rewrite the radicand as a product of the square root of 36 and its matching factor: \( \sqrt{72} = \sqrt{36 \cdot 2} \).
Apply the product rule: Use the property \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \) to separate the factors.
Continuing the example:
- Apply the product rule: \( \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} \).
Simplify: Take the square root of the perfect square and multiply by the remaining square root.
For \( \sqrt{72} \):
- Simplify \( \sqrt{36} \) to 6.
- Combine the results: \( 6 \sqrt{2} \).
- Thus, \( \sqrt{72} = 6 \sqrt{2} \).
Examples:
Simplify \( \sqrt{32} \):
- The largest perfect square factor of 32 is 16.
- Rewrite: \( \sqrt{32} = \sqrt{16 \cdot 2} \).
- Apply the product rule: \( \sqrt{16} \cdot \sqrt{2} \).
- Simplify \( \sqrt{16} \) to 4.
- Final answer: \( 4 \sqrt{2} \).
Simplify \( \sqrt{50} \):
- The largest perfect square factor of 50 is 25.
- Rewrite: \( \sqrt{50} = \sqrt{25 \cdot 2} \).
- Apply the product rule: \( \sqrt{25} \cdot \sqrt{2} \).
- Simplify \( \sqrt{25} \) to 5.
- Final answer: \( 5 \sqrt{2} \).
Special Cases:
If the radicand is a prime number, it cannot be simplified further (e.g., \( \sqrt{13} \) remains \( \sqrt{13} \)).
If the radicand is a perfect square, the square root will be an integer (e.g., \( \sqrt{64} = 8 \)).
By following these steps, you can simplify radicals efficiently and accurately.

Common Mistakes and How to Avoid Them
When simplifying square roots, students often encounter several common pitfalls. Recognizing and avoiding these mistakes can lead to more accurate and confident problem-solving.
- Forgetting to Check for Perfect Squares: Always look for perfect square factors within the radicand (the number under the square root). For instance, in simplifying , recognize that 72 can be broken down into . Since 36 is a perfect square, it simplifies to .
- Misapplying Properties of Radicals: Ensure correct application of properties such as and . Incorrectly applying these properties can lead to errors. For example, .
- Rushing Through Simplification: Simplification should be done methodically. Skipping steps or rushing can cause errors. Take your time to ensure each factor is accounted for correctly.
- Ignoring Negative Signs: Remember that the square root of a negative number introduces an imaginary number. For example, , not 5.
How to Avoid These Mistakes
To overcome these common errors, follow these strategies:
- Practice Regularly: The more you practice, the more familiar you become with different types of problems and the process of simplification.
- Review Properties of Radicals: Regularly review the properties of radicals and exponents to ensure you apply them correctly.
- Double-Check Your Work: Always take a moment to go over your work to catch any mistakes you might have made.
- Use Online Resources and Tools: Utilize math forums, apps, and calculators to get different perspectives and check your work.
By being aware of these common mistakes and taking steps to avoid them, you can improve your skills in simplifying square roots and achieve greater accuracy and confidence in your mathematical work.
Using Square Root Calculators
Square root calculators are useful tools for simplifying square roots, especially for large numbers or complex expressions. Here are the steps to use a square root calculator effectively:
Step-by-Step Instructions
- Open a square root calculator tool online. Some popular ones include the and the .
- Enter the number or expression you need to simplify into the input box. For example, if you want to simplify the square root of 72, enter "72".
- Click on the "Calculate" or "Simplify" button to process your input.
- The calculator will provide the simplified form of the square root. For instance, it will show \( \sqrt{72} = 6\sqrt{2} \).
Features of Square Root Calculators
- Exact and Approximate Values: Most calculators provide both the exact simplified form and an approximate decimal value. For example, \( \sqrt{50} = 5\sqrt{2} \approx 7.071 \).
- Step-by-Step Solutions: Some calculators offer detailed steps, showing the factorization and simplification process. This can be particularly helpful for learning and verification purposes.
- Handling Complex Numbers: Advanced calculators can also deal with negative numbers, providing complex roots (e.g., \( \sqrt{-1} = i \)).
Examples
| Expression | Simplified Form | Approximate Value |
|---|---|---|
| \( \sqrt{50} \) | \( 5\sqrt{2} \) | \( \approx 7.071 \) |
| \( \sqrt{32} \) | \( 4\sqrt{2} \) | \( \approx 5.657 \) |
| \( \sqrt{18} \) | \( 3\sqrt{2} \) | \( \approx 4.243 \) |
Using a square root calculator can save time and help ensure accuracy in your calculations. Whether you're working on homework, preparing for a test, or solving complex mathematical problems, these tools are invaluable resources.
Practice Problems and Solutions
Practicing square root problems is an excellent way to understand and master the concept. Below are some practice problems along with step-by-step solutions to help you grasp the process of simplifying square roots.
Problem 1
Simplify \( \sqrt{49} \).
Solution:
- Recognize that 49 is a perfect square.
- Find the square root of 49.
- \( \sqrt{49} = 7 \)
Problem 2
Simplify \( \sqrt{75} \).
Solution:
- Factor 75 into prime factors: \( 75 = 3 \times 5^2 \).
- Rewrite the square root: \( \sqrt{75} = \sqrt{3 \times 5^2} \).
- Separate the perfect square: \( \sqrt{75} = \sqrt{3} \times \sqrt{5^2} \).
- Simplify: \( \sqrt{75} = 5\sqrt{3} \).
Problem 3
Simplify \( \sqrt{18} \).
Solution:
- Factor 18 into prime factors: \( 18 = 2 \times 3^2 \).
- Rewrite the square root: \( \sqrt{18} = \sqrt{2 \times 3^2} \).
- Separate the perfect square: \( \sqrt{18} = \sqrt{2} \times \sqrt{3^2} \).
- Simplify: \( \sqrt{18} = 3\sqrt{2} \).
Problem 4
Simplify \( \sqrt{200} \).
Solution:
- Factor 200 into prime factors: \( 200 = 2^3 \times 5^2 \).
- Rewrite the square root: \( \sqrt{200} = \sqrt{2^3 \times 5^2} \).
- Separate the perfect squares: \( \sqrt{200} = \sqrt{2^2 \times 5^2 \times 2} \).
- Simplify: \( \sqrt{200} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2} \).
Problem 5
Simplify \( \sqrt{50} \).
Solution:
- Factor 50 into prime factors: \( 50 = 2 \times 5^2 \).
- Rewrite the square root: \( \sqrt{50} = \sqrt{2 \times 5^2} \).
- Separate the perfect square: \( \sqrt{50} = \sqrt{2} \times \sqrt{5^2} \).
- Simplify: \( \sqrt{50} = 5\sqrt{2} \).
Problem 6
Simplify \( \sqrt{72} \).
Solution:
- Factor 72 into prime factors: \( 72 = 2^3 \times 3^2 \).
- Rewrite the square root: \( \sqrt{72} = \sqrt{2^3 \times 3^2} \).
- Separate the perfect squares: \( \sqrt{72} = \sqrt{2^2 \times 3^2 \times 2} \).
- Simplify: \( \sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
Problem 7
Simplify \( \sqrt{32} \).
Solution:
- Factor 32 into prime factors: \( 32 = 2^5 \).
- Rewrite the square root: \( \sqrt{32} = \sqrt{2^4 \times 2} \).
- Separate the perfect square: \( \sqrt{32} = \sqrt{2^4} \times \sqrt{2} \).
- Simplify: \( \sqrt{32} = 4\sqrt{2} \).
Problem 8
Simplify \( \sqrt{48} \).
Solution:
- Factor 48 into prime factors: \( 48 = 2^4 \times 3 \).
- Rewrite the square root: \( \sqrt{48} = \sqrt{2^4 \times 3} \).
- Separate the perfect square: \( \sqrt{48} = \sqrt{2^4} \times \sqrt{3} \).
- Simplify: \( \sqrt{48} = 4\sqrt{3} \).
Problem 9
Simplify \( \sqrt{12} \).
Solution:
- Factor 12 into prime factors: \( 12 = 2^2 \times 3 \).
- Rewrite the square root: \( \sqrt{12} = \sqrt{2^2 \times 3} \).
- Separate the perfect square: \( \sqrt{12} = \sqrt{2^2} \times \sqrt{3} \).
- Simplify: \( \sqrt{12} = 2\sqrt{3} \).
Problem 10
Simplify \( \sqrt{27} \).
Solution:
- Factor 27 into prime factors: \( 27 = 3^3 \).
- Rewrite the square root: \( \sqrt{27} = \sqrt{3^2 \times 3} \).
- Separate the perfect square: \( \sqrt{27} = \sqrt{3^2} \times \sqrt{3} \).
- Simplify: \( \sqrt{27} = 3\sqrt{3} \).
Additional Resources
- : A user-friendly online tool for calculating and simplifying square roots.
- : Provides step-by-step solutions to simplify square roots and offers additional features like graphing and equation solving.
- : Simple and intuitive calculator for computing square roots of numbers.
- : Offers a comprehensive algebra solver that includes tools for simplifying square roots.
- : Provides a straightforward interface for calculating square roots with explanations.
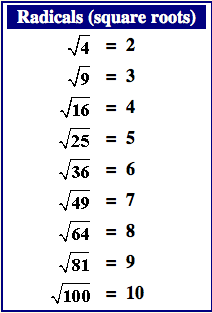
Hãy xem video này để học cách giản đơn các căn bậc hai bằng cây nhân bội trong đại số. Phần 1 của loạt video giải thích chi tiết về biểu thức căn bậc hai và cách thực hiện quy trình giản đơn.
01 - Giản đơn Các rễ bình phương với cây nhân bội trong đại số (Biểu thức lập phương căn), Phần 1
READ MORE:
Hãy xem video này để học cách giản đơn các căn bậc hai trong toán học với thầy J. Video cung cấp những phương pháp và ví dụ cụ thể về cách giản đơn biểu thức căn bậc hai.
Giản đơn Các căn bậc hai | Toán học với thầy J