Topic square root of 72 in radical form: Understanding the square root of 72 in radical form is essential for mastering algebraic concepts. This guide provides a comprehensive, step-by-step approach to simplifying √72, ensuring clarity and ease of learning. By breaking down the process, you'll gain confidence in handling similar problems and enhancing your mathematical skills.
Table of Content
- Square Root of 72 in Radical Form
- Introduction to Square Roots
- Understanding Radical Expressions
- Simplifying Square Roots
- Steps to Simplify √72
- Perfect Squares and Their Role
- Extracting Factors from Radicals
- Combining Simplified Factors
- Final Simplified Form of √72
- Applications of Simplified Radicals
- Common Mistakes to Avoid
- Practice Problems and Solutions
- Additional Resources and References
- Conclusion
- YOUTUBE:
Square Root of 72 in Radical Form
The square root of 72 can be simplified by expressing it in its radical form. This involves finding the prime factors of 72 and then simplifying the radical expression.
Prime Factorization of 72
To begin with, let's find the prime factors of 72:
- 72 ÷ 2 = 36
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
So, the prime factorization of 72 is:
72 = 2 × 2 × 2 × 3 × 3
Simplifying the Radical Expression
Next, we can simplify the square root of 72 by grouping the prime factors into pairs:
√72 = √(2 × 2 × 2 × 3 × 3)
We can pair the factors as follows:
√72 = √((2 × 2) × (3 × 3) × 2)
√72 = √(4 × 9 × 2)
Extracting Perfect Squares
Since 4 and 9 are perfect squares, we can take their square roots outside the radical:
√72 = √4 × √9 × √2
√72 = 2 × 3 × √2
Final Simplified Form
Thus, the simplified radical form of the square root of 72 is:
√72 = 6√2

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, particularly in algebra and geometry. A square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because 3 × 3 = 9.
Square roots are denoted by the radical symbol (√). The number under the radical symbol is called the radicand. For example, in √72, 72 is the radicand.
Understanding square roots involves recognizing perfect squares and simplifying radicals. Perfect squares are numbers like 1, 4, 9, 16, and so on, which are the squares of integers. Simplifying radicals means expressing them in their simplest form by factoring out perfect squares.
- Identify the radicand: The number under the radical sign (√).
- Find the prime factors of the radicand: Break down the number into its prime factors.
- Group the prime factors into pairs: This helps in identifying the perfect squares.
- Simplify by extracting the perfect squares: Take the square root of the perfect squares and place them outside the radical.
By following these steps, you can simplify square roots efficiently. This process not only makes calculations easier but also helps in understanding the properties of numbers and their relationships.
Understanding Radical Expressions
Radical expressions involve roots, such as square roots, cube roots, and so on. The most common radical expression is the square root, represented by the radical symbol (√). In a radical expression like √72, the number inside the radical symbol is called the radicand, which is 72 in this case.
To understand radical expressions, it's essential to grasp the following concepts:
- Radicand: The number inside the radical symbol. For example, in √72, 72 is the radicand.
- Index: The small number outside and to the left of the radical symbol indicating the root. If no index is written, it is assumed to be 2 (square root).
- Simplification: The process of reducing the radical expression to its simplest form. This involves factoring the radicand and extracting the square factors.
Here's a step-by-step guide to simplify a radical expression like √72:
- Identify the radicand: In this case, the radicand is 72.
- Find the prime factors of the radicand: 72 can be factored into 2 × 2 × 2 × 3 × 3.
- Group the prime factors into pairs: (2 × 2) and (3 × 3).
- Simplify by extracting the perfect squares: √(2 × 2 × 2 × 3 × 3) = √(4 × 9 × 2).
- Take the square root of the perfect squares: √4 = 2 and √9 = 3.
- Multiply the results outside the radical: 2 × 3 = 6.
- Combine with the remaining factor inside the radical: 6√2.
Therefore, the simplified form of √72 is 6√2. Understanding and simplifying radical expressions are crucial for solving algebraic equations and understanding more complex mathematical concepts.
Simplifying Square Roots
Simplifying square roots involves expressing the radical in its simplest form by factoring out perfect squares. This process makes the expression easier to work with in equations and other mathematical operations. Here’s a detailed, step-by-step guide to simplifying the square root of 72:
- Identify the radicand: The number under the square root symbol is called the radicand. In this case, the radicand is 72.
- Prime factorize the radicand: Break down 72 into its prime factors.
- 72 ÷ 2 = 36
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
So, 72 can be expressed as 2 × 2 × 2 × 3 × 3.
- Group the prime factors into pairs: Look for pairs of the same number.
- (2 × 2) and (3 × 3)
Therefore, 72 = 23 × 32.
- Simplify by extracting the perfect squares: For each pair of identical factors, take one factor out of the square root.
- √72 = √(2 × 2 × 2 × 3 × 3)
- √72 = √(4 × 9 × 2)
- √72 = √4 × √9 × √2
- Calculate the square roots of the perfect squares:
- √4 = 2
- √9 = 3
- Multiply the results outside the radical:
- 2 × 3 = 6
So, the simplified form is:
√72 = 6√2
By following these steps, you can simplify the square root of any number, not just 72. This method of breaking down the radicand into prime factors and extracting perfect squares is fundamental to working with radical expressions effectively.
Steps to Simplify √72
To simplify the square root of 72, follow these steps:
-
Factor the number 72 into its prime factors:
-
Group the prime factors into pairs:
-
Take the square root of each pair:
-
Simplify by taking the square roots out of the radical:
-
Multiply the simplified terms:
Thus, the simplified form of is .

Perfect Squares and Their Role
Perfect squares play a crucial role in simplifying square roots. A perfect square is a number that can be expressed as the square of an integer. For example, 1, 4, 9, 16, 25, and 36 are all perfect squares because they are the squares of 1, 2, 3, 4, 5, and 6, respectively.
When simplifying square roots, identifying and using perfect squares helps to break down the radicand into more manageable parts. Here's how perfect squares are utilized:
- Factorization: First, factor the number under the square root into its prime factors. Look for pairs of prime factors, as these will form perfect squares.
- Separating Perfect Squares: Use the property of square roots that allows the square root of a product to be expressed as the product of the square roots. This means \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Extracting Factors: For each pair of factors, take one out of the square root sign. This simplification is possible because the square root of a perfect square is an integer.
For example, to simplify \( \sqrt{72} \), follow these steps:
- Factorize 72 into its prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Group the factors into pairs: \( 72 = (2 \times 2) \times (3 \times 3) \times 2 = 4 \times 9 \times 2 \).
- Separate the perfect squares: \( \sqrt{72} = \sqrt{4 \times 9 \times 2} = \sqrt{4} \times \sqrt{9} \times \sqrt{2} \).
- Simplify each square root: \( \sqrt{4} = 2 \) and \( \sqrt{9} = 3 \).
- Combine the simplified factors: \( 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
Thus, the simplified form of \( \sqrt{72} \) is \( 6\sqrt{2} \). Understanding and utilizing perfect squares make this process straightforward and systematic.
Extracting Factors from Radicals
To simplify a square root expression like √72, it's essential to extract factors, especially focusing on perfect squares. Here's a step-by-step guide:
- Identify Factors of 72:
First, list all factors of 72:
- 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
- Find the Largest Perfect Square Factor:
Next, identify the perfect squares among these factors. Perfect squares are numbers like 1, 4, 9, 16, 25, 36, etc. For 72, the perfect square factors are:
- 1, 4, 9, 36
The largest perfect square factor of 72 is 36.
- Rewrite the Square Root:
Express √72 using its factors, specifically the largest perfect square:
\[
\sqrt{72} = \sqrt{36 \times 2}
\] - Apply the Product Rule for Radicals:
According to the product rule, the square root of a product is the product of the square roots. Hence, you can separate the radical expression:
\[
\sqrt{72} = \sqrt{36} \times \sqrt{2}
\] - Simplify the Expression:
Calculate the square root of the perfect square factor. The square root of 36 is 6:
\[
\sqrt{36} = 6
\]Therefore, you can now simplify the original expression:
\[
\sqrt{72} = 6 \times \sqrt{2}
\] - Final Simplified Form:
The simplified form of √72 is:
\[
\sqrt{72} = 6\sqrt{2}
\]
By extracting and simplifying the factors, you can transform complex radical expressions into simpler forms, making calculations easier and more intuitive.
Combining Simplified Factors
Once we have extracted the factors from under the radical, the next step is to combine these simplified factors to achieve the final simplified form of the square root expression. Here is a detailed step-by-step guide to combining simplified factors for the square root of 72:
Identify the Simplified Factors:
After prime factorization and extracting perfect squares, we have the simplified form of the square root of 72 as:
\[ \sqrt{72} = \sqrt{36 \times 2} \]
Since 36 is a perfect square, we simplify it to get:
\[ \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} \]
Simplify the Perfect Square:
We know that \(\sqrt{36} = 6\). Therefore, the expression becomes:
\[ 6 \times \sqrt{2} \]
Combine the Simplified Factors:
After simplifying, the square root expression is:
\[ \sqrt{72} = 6\sqrt{2} \]
This is the final simplified form of \(\sqrt{72}\) in radical form.
Here is a table summarizing the steps:
| Step | Expression |
|---|---|
| Prime Factorization | \( 72 = 2^3 \times 3^2 \) |
| Extract Perfect Squares | \( \sqrt{72} = \sqrt{36 \times 2} \) |
| Simplify Perfect Squares | \( \sqrt{36 \times 2} = 6 \times \sqrt{2} \) |
| Combine Factors | \( 6\sqrt{2} \) |
By following these steps, we can simplify any square root expression efficiently. Practicing with different numbers will help in mastering the technique of combining simplified factors.
Final Simplified Form of √72
The square root of 72 can be simplified by expressing it in terms of its prime factors and then simplifying the radical. Here are the steps to achieve the final simplified form:
First, perform the prime factorization of 72:
72 = 2 × 36
36 is also a composite number, so we can break it down further:
36 = 6 × 6
And 6 can be broken down into prime factors:
6 = 2 × 3
Thus, the prime factorization of 72 is:
72 = 2 × 2 × 2 × 3 × 3
Next, group the prime factors into pairs of equal factors:
(2 × 2) × (3 × 3) × 2
Now, apply the property of square roots that allows you to take the square root of each pair of factors:
√72 = √[(2 × 2) × (3 × 3) × 2]
Simplify each pair inside the radical:
√[(2 × 2)] = 2
√[(3 × 3)] = 3
Combine the simplified factors outside the radical and multiply them with the remaining factor inside the radical:
√72 = 2 × 3 × √2
Therefore, the final simplified form of √72 is:
√72 = 6√2
Expressing the square root in its simplest radical form makes it easier to understand and use in further calculations. The final simplified form of √72 is 6√2, where 6 is the product of the square roots of the paired factors, and √2 is the remaining factor.
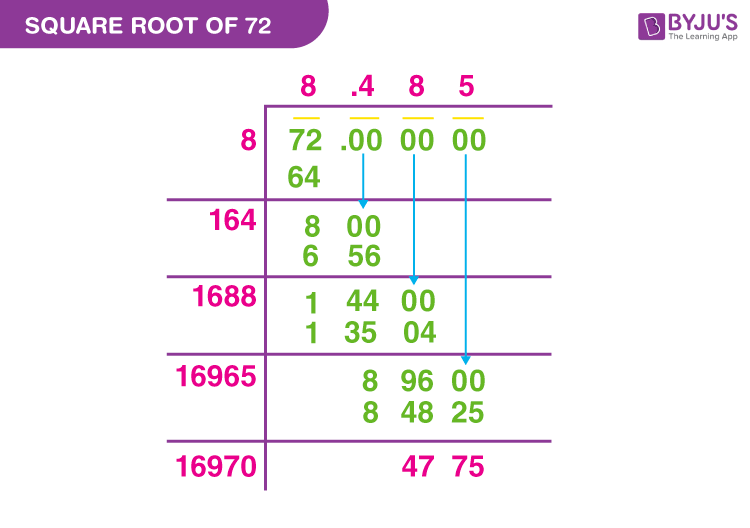
Applications of Simplified Radicals
Simplified radicals, such as the square root of 72 simplified to \( 6\sqrt{2} \), have various practical applications in different fields. Understanding these applications can help in comprehending their importance and utility in real-world scenarios.
- Mathematics and Algebra: Simplified radicals are frequently used in algebra to solve equations and inequalities. For instance, they are utilized in quadratic equations, simplifying complex expressions, and in functions involving roots.
- Geometry: Radicals play a critical role in geometry, especially in calculating distances and areas. For example, the length of the diagonal of a square with side length \( s \) is \( s\sqrt{2} \). Similarly, the Pythagorean theorem, \( a^2 + b^2 = c^2 \), often results in radical expressions when solving for the hypotenuse or other sides of a right triangle.
- Physics: In physics, radicals are used to express quantities such as velocity, acceleration, and force. For example, the formula for the period \( T \) of a simple pendulum is \( T = 2\pi\sqrt{\frac{L}{g}} \), where \( L \) is the length of the pendulum and \( g \) is the acceleration due to gravity.
- Engineering: Engineers use radicals to solve problems involving electrical circuits, structural analysis, and material strength. The resonance frequency \( f \) of an LC circuit is given by \( f = \frac{1}{2\pi\sqrt{LC}} \), where \( L \) is inductance and \( C \) is capacitance.
- Computer Science: Algorithms often use radical expressions to optimize performance and calculations. For example, the Euclidean distance formula, \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \), is used in clustering algorithms and computer graphics.
Simplifying radicals makes it easier to work with these expressions, enhancing clarity and precision in calculations across various disciplines.
Common Mistakes to Avoid
Simplifying square roots can be straightforward, but common mistakes can lead to incorrect results. Here are some key mistakes to avoid when simplifying the square root of 72 and other similar radicals:
- Not Fully Factorizing: Ensure that you break down the number completely into its prime factors. For example, the prime factorization of 72 is \(2^3 \times 3^2\). Missing any factors can lead to an incomplete simplification.
- Overlooking Pairs of Factors: Each pair of identical factors under the square root should be taken out as a single factor. In the case of 72, pairs of \(2\)s and \(3\)s need to be extracted correctly.
- Misplacing Factors: When extracting factors from under the radical, ensure they are multiplied correctly outside the radical. For instance, for \( \sqrt{72} \), extracting pairs gives \(2 \times 3 = 6\) outside the radical, leaving \( \sqrt{2} \) inside.
- Ignoring Remaining Factors: Any factors that do not form pairs should remain under the square root. In \( \sqrt{72} \), after extracting pairs of \(2\) and \(3\), the remaining \( \sqrt{2} \) must be included.
- Confusing Addition and Multiplication: Remember that the rules for simplifying square roots involve multiplication of factors, not addition. This confusion can lead to incorrect results.
By being aware of these common pitfalls and taking care to avoid them, you can simplify square roots accurately and enhance your understanding of mathematical concepts.
Practice Problems and Solutions
Practicing simplifying square roots is essential for mastering the concept. Below are some practice problems along with detailed solutions to help you understand the process of simplifying square roots, particularly focusing on the square root of 72.
Practice Problems
- Simplify \( \sqrt{72} \)
- Simplify \( \sqrt{50} \)
- Simplify \( \sqrt{98} \)
- Simplify \( \sqrt{128} \)
- Simplify \( \sqrt{200} \)
Solutions
-
Simplify \( \sqrt{72} \):
- Factor 72 into prime factors: \( 72 = 2^3 \times 3^2 \).
- Group the factors into pairs: \( 72 = (2^2 \times 3^2) \times 2 \).
- Take the square root of each group: \( \sqrt{72} = \sqrt{(2^2 \times 3^2) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
-
Simplify \( \sqrt{50} \):
- Factor 50 into prime factors: \( 50 = 2 \times 5^2 \).
- Group the factors into pairs: \( 50 = 2 \times (5^2) \).
- Take the square root of each group: \( \sqrt{50} = \sqrt{2 \times (5^2)} = 5\sqrt{2} \).
-
Simplify \( \sqrt{98} \):
- Factor 98 into prime factors: \( 98 = 2 \times 7^2 \).
- Group the factors into pairs: \( 98 = 2 \times (7^2) \).
- Take the square root of each group: \( \sqrt{98} = \sqrt{2 \times (7^2)} = 7\sqrt{2} \).
-
Simplify \( \sqrt{128} \):
- Factor 128 into prime factors: \( 128 = 2^7 \).
- Group the factors into pairs: \( 128 = (2^6) \times 2 = (2^3)^2 \times 2 \).
- Take the square root of each group: \( \sqrt{128} = \sqrt{(2^3)^2 \times 2} = 2^3 \times \sqrt{2} = 8\sqrt{2} \).
-
Simplify \( \sqrt{200} \):
- Factor 200 into prime factors: \( 200 = 2^3 \times 5^2 \).
- Group the factors into pairs: \( 200 = (2^2 \times 5^2) \times 2 \).
- Take the square root of each group: \( \sqrt{200} = \sqrt{(2^2 \times 5^2) \times 2} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2} \).
By practicing these problems, you can become more comfortable with simplifying square roots and applying these skills to various mathematical contexts.
Additional Resources and References
For those looking to deepen their understanding of simplifying square roots, particularly the square root of 72, the following resources and references offer valuable insights, tools, and practice problems:
- Symbolab: Simplify Radicals
Symbolab provides a comprehensive tool to simplify radical expressions. Their step-by-step solutions can help you understand the process of simplifying √72 and similar problems.
Visit:
- MathWarehouse: Simplest Radical Form
MathWarehouse offers detailed explanations and examples of how to simplify square roots, including the square root of 72. Their clear and concise steps make it easy to follow along.
Visit:
- Cuemath: Square Root Calculations
Cuemath provides interactive examples and illustrations to help visualize and simplify the square root of 72. Their approach to teaching mathematical concepts through visuals is particularly helpful for learners of all levels.
Visit:
- MathOnDemand: Step-by-Step Solutions
MathOnDemand offers a detailed breakdown of the simplification process for the square root of 72, using the product rule for radicals. This resource is great for those who prefer a systematic, methodical approach.
Visit:
- Interactive Tutorials and Practice Problems
For additional practice, there are numerous online platforms that provide interactive tutorials and practice problems. Websites like Khan Academy and Purplemath are excellent for reinforcing concepts and ensuring mastery of simplifying square roots.
Visit:
Visit:
These resources provide extensive practice and theoretical knowledge to help you master the process of simplifying square roots and understanding their applications in various mathematical contexts.

Conclusion
The process of simplifying the square root of 72, which results in \( 6\sqrt{2} \), showcases the importance of understanding radical expressions and their applications. By breaking down the number into its prime factors and identifying perfect squares, we can simplify complex radicals into more manageable forms. This method is not only useful for solving mathematical problems but also for applications in various fields such as physics, engineering, and computer science.
Understanding how to simplify radicals like \( \sqrt{72} \) helps in grasping more advanced mathematical concepts and solving real-world problems efficiently. It reinforces the fundamentals of algebra and provides a solid foundation for further studies in mathematics and related disciplines. The ability to simplify radicals enhances problem-solving skills and promotes logical thinking, which are essential in both academic and professional settings.
By mastering the techniques of simplifying square roots, students and professionals alike can tackle a wide range of mathematical challenges with confidence. This skill not only aids in academic success but also opens up opportunities for innovation and discovery in scientific and technological fields. As you continue to explore the world of mathematics, remember that every complex problem can be broken down into simpler parts, just like how we simplified \( \sqrt{72} \) into \( 6\sqrt{2} \).
In conclusion, the journey of simplifying the square root of 72 exemplifies the beauty and utility of mathematics. It highlights the importance of foundational knowledge and the continuous pursuit of learning. Keep practicing, stay curious, and embrace the power of mathematics in unraveling the mysteries of the universe.
Radicals: Đơn Giản Hóa √(72)
READ MORE:
Hướng dẫn chi tiết cách tính căn bậc hai của 72, giúp bạn hiểu rõ và nắm vững cách tính sqrt(72).
Cách Tính Căn Bậc Hai của 72: Sqrt(72)












