Simplify Square Root Expressions Calculator: Your Ultimate Guide

Welcome to our comprehensive guide on simplifying square root expressions using a calculator. This tool is designed to help you effortlessly break down complex square root expressions into their simplest form. Read on to discover how you can make the most of this powerful tool!

What is Simplifying Square Root Expressions?

Simplifying square root expressions involves breaking down a square root into its simplest possible form. This process often includes identifying perfect square factors and using properties of radicals to simplify.

Why Use a Calculator?

Using a calculator to simplify square root expressions saves time and reduces the possibility of errors. It allows you to focus on understanding the concepts rather than getting bogged down by manual calculations.

How to Use the Simplify Square Root Expressions Calculator

1. Enter the square root expression you want to simplify into the calculator.
2. Click on the "Simplify" button.
3. The calculator will provide you with the simplified form of the expression, step-by-step.

Example: Simplifying $\surd 128$

To simplify $\surd 128$, follow these steps:

• Identify the perfect square factors of 128. In this case, 128 can be factored into 64 and 2.
• Write the expression as the product of the square root of the perfect square and the square root of the remaining factor: $\surd 128\; =\; \surd (64\; \times \; 2)$.
• Simplify further: $\surd 128\; =\; \surd 64\; \times \; \surd 2\; =\; 8\surd 2$.

Benefits of Using Our Calculator

Our simplify square root expressions calculator offers several benefits:

• Accuracy: Provides precise results every time.
• Speed: Quickly simplifies complex expressions.
• Convenience: Easy to use, with a user-friendly interface.
• Educational: Shows step-by-step solutions to enhance your understanding.

Conclusion

Simplifying square root expressions doesn't have to be a daunting task. With our simplify square root expressions calculator, you can achieve accurate and simplified results in no time. Try it out today and enhance your mathematical skills!

Simplifying square root expressions is an essential skill in algebra, allowing for cleaner and more manageable equations. This process involves reducing a square root to its simplest form, making it easier to work with in mathematical operations and problem-solving.

Understanding how to simplify square root expressions can be broken down into several key steps:

• Identifying the factors of the radicand (the number inside the square root).
• Determining which factors are perfect squares.
• Extracting the square root of the perfect squares.
• Rewriting the expression in its simplest form.

For example, consider the expression \(\sqrt{50}\):

1. Factor 50 into 25 and 2.
2. Recognize that 25 is a perfect square (\(25 = 5^2\)).
3. Simplify the square root: \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\).

By following these steps, you can simplify square root expressions effectively. This is particularly useful in solving radical equations and simplifying algebraic expressions involving roots. Utilizing a calculator designed for simplifying square root expressions can further streamline this process, providing step-by-step solutions and ensuring accuracy in your calculations.

Square roots are fundamental mathematical concepts that allow us to determine the original number that was squared to produce a given value. A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). The symbol for the square root is \( \sqrt{} \).

For example, \( \sqrt{25} = 5 \) because \( 5^2 = 25 \). There are both positive and negative square roots for any positive number, but the principal (or positive) square root is the one most commonly used.

Perfect Squares

Perfect squares are numbers that are the square of an integer. For instance, the numbers 1, 4, 9, 16, 25, and 36 are all perfect squares because they can be written as \( 1^2 \), \( 2^2 \), \( 3^2 \), \( 4^2 \), \( 5^2 \), and \( 6^2 \) respectively.

Simplifying Square Roots

Simplifying square roots involves expressing the square root in its simplest form. To simplify a square root:

1. Find the prime factors of the number inside the square root.
2. Group the prime factors into pairs.
3. Move one factor from each pair outside the square root.

For example, to simplify \( \sqrt{72} \):

• Prime factors of 72 are \( 2 \times 2 \times 2 \times 3 \times 3 \).
• Group the factors into pairs: \( (2 \times 2) \) and \( (3 \times 3) \).
• Move one factor from each pair outside the square root: \( 2 \times 3 \).

So, \( \sqrt{72} = 6\sqrt{2} \).

Properties of Square Roots

Using these properties, you can simplify more complex square root expressions.

Understanding and simplifying square roots is essential in algebra and helps in solving quadratic equations and other mathematical problems involving radicals.

The simplification of square root expressions is a crucial aspect of algebra that helps in making calculations easier and expressions more manageable. Here are the basic principles:

1. Identifying Perfect Squares: A key step in simplification is recognizing perfect squares within the radicand. For instance, in \(\sqrt{36}\), 36 is a perfect square.
2. Prime Factorization: Break down the radicand into its prime factors. For example, for \(\sqrt{72}\): \[ 72 = 2 \times 2 \times 2 \times 3 \times 3. \]
3. Grouping Factors: Group the prime factors into pairs. Each pair can be taken out of the square root. For \(\sqrt{72}\), the pairs are: \[ 2 \times 2 \text{ and } 3 \times 3. \]
4. Extracting Factors: Extract each pair as a single factor outside the square root: \[ \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}. \]

By following these steps, you can simplify any square root expression effectively. This process not only simplifies the expression but also makes it easier to work with in further mathematical operations.

Perfect squares are numbers that are the result of an integer multiplied by itself. For example, 1, 4, 9, 16, and 25 are perfect squares because they can be expressed as \(1^2\), \(2^2\), \(3^2\), \(4^2\), and \(5^2\) respectively. Identifying perfect squares is crucial in simplifying square root expressions.

How to Identify Perfect Squares

To identify perfect squares, follow these steps:

1. Factor the number into its prime factors.
2. Check if each prime factor appears an even number of times.
3. If all prime factors pair up evenly, the number is a perfect square.

Here are some examples:

• 16 can be factored into \(2 \times 2 \times 2 \times 2\), which is \(4^2\), making 16 a perfect square.
• 25 can be factored into \(5 \times 5\), which is \(5^2\), making 25 a perfect square.
• 18 can be factored into \(2 \times 3 \times 3\), where 2 doesn't pair, so 18 is not a perfect square.

Using Perfect Squares to Simplify Square Roots

Knowing whether a number is a perfect square helps in simplifying square roots. For example:

• The square root of 49 is 7 because \(7^2 = 49\).
• The square root of 81 is 9 because \(9^2 = 81\).
• The square root of 20 can be simplified by factoring it into \(4 \times 5\), which gives us \(2\sqrt{5}\) since 4 is a perfect square.

Identifying and using perfect squares can significantly simplify complex square root expressions, making calculations easier and more efficient.

Simplifying square root expressions involves breaking down the expression into its simplest form. Below is a step-by-step guide to simplify square root expressions.

1. Identify the Radicand:

   The radicand is the number inside the square root. For example, in \(\sqrt{50}\), the radicand is 50.

2. Prime Factorization:

   Find the prime factors of the radicand. For 50, the prime factors are 2 and 5 (since \(50 = 2 \times 5^2\)).

3. Group the Factors:

   Group the factors into pairs of equal factors. In our example, \(50 = 2 \times 5^2\), we have one pair of 5.

4. Apply the Square Root:

   Take the square root of each pair of factors. For each pair, one factor comes out of the square root. For \( \sqrt{2 \times 5^2} \), the square root of \(5^2\) is 5, and the 2 remains inside the square root:

   \(\sqrt{2 \times 5^2} = 5 \sqrt{2}\)

5. Simplify the Expression:

   Combine the results to get the simplified form of the original expression. Hence, \(\sqrt{50} = 5 \sqrt{2}\).

Let's consider another example for practice:

Example: Simplify \(\sqrt{72}\)

• Step 1: Prime Factorization of 72: \(72 = 2^3 \times 3^2\)
• Step 2: Group the factors: \(72 = (2^2 \times 2) \times 3^2\)
• Step 3: Apply the square root: \(\sqrt{2^2 \times 2 \times 3^2} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}\)

By following these steps, you can simplify any square root expression. Using a square root calculator can help you verify your results and understand the process better.

Here are some general rules to keep in mind:

• Product Rule: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\)
• Quotient Rule: \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\)

A simplify square root expressions calculator is an excellent tool for quickly and accurately simplifying radical expressions. Here’s how to use it effectively:

1. Open the Calculator: Navigate to a reliable simplify square root expressions calculator online, such as those available on CalculatorSoup or OmniCalculator.

2. Input the Expression: Enter the radical expression you want to simplify. The calculator typically has fields for the coefficient (if any), the radicand (the number under the radical), and the index (the root degree, which is 2 for square roots).

   • For example, to simplify \(3\sqrt{72}\), you would enter 3 in the coefficient field and 72 in the radicand field, leaving the index at its default of 2.

3. Prime Factorization: The calculator will break down the radicand into its prime factors. For \( \sqrt{72} \), the factors are \( 2^3 \times 3^2 \).

4. Simplify the Expression: The calculator simplifies the radical by extracting pairs of prime factors. For \( \sqrt{72} \), the simplification would be \( 6\sqrt{2} \), because \( 72 = 36 \times 2 \) and \( \sqrt{36} = 6 \).

5. View the Steps: Most calculators will show you the step-by-step process of how they arrived at the simplified form. This feature is beneficial for learning and verifying the steps manually.

6. Final Answer: The calculator will display the simplified form of the expression. In our example, \( 3\sqrt{72} \) simplifies to \( 18\sqrt{2} \).

Using a simplify square root expressions calculator can save time and reduce errors, especially with complex expressions. Additionally, these calculators often provide additional functionalities, such as handling cube roots and other higher-order roots, as well as simplifying sums, products, and quotients of radical expressions.

Using a calculator to simplify square root expressions offers numerous benefits that enhance both efficiency and accuracy in mathematical computations. Here are some key advantages:

• Efficiency: Calculators automate the simplification process, handling large numbers and complex calculations much faster than manual methods. This saves significant time and effort.
• Accuracy: Calculators provide precise results, ensuring that the simplified expression is accurate. This reduces the risk of human error in manual calculations.
• Handling Large Numbers: Calculators can process very large numbers and provide their square roots quickly, a task that is often impractical to perform manually.
• User-Friendly Interface: Most calculators are designed with intuitive interfaces, making them accessible even for users with limited mathematical expertise. This ease of use encourages wider adoption and reduces the learning curve.
• Step-by-Step Solutions: Many calculators offer detailed, step-by-step solutions. This educational feature helps users understand the simplification process and learn the underlying mathematical principles.
• Support for Complex Numbers: Advanced calculators can handle not only real numbers but also complex and imaginary numbers, providing solutions that are beyond the scope of basic manual methods.
• Scientific Notation Support: Calculators often support scientific notation, making it easier to work with very large or very small numbers and understand their simplified forms.
• Quick Data Insights: Instantaneous results allow users to quickly grasp the simplified form of a square root expression, facilitating faster decision-making in practical applications.
• Educational Tool: Calculators serve as valuable educational tools, helping students and learners practice and understand square root simplification, reinforcing their mathematical skills.
• Real-World Applications: The ability to quickly and accurately simplify square roots is beneficial in various fields such as engineering, physics, computer science, and finance, where such calculations are frequently required.

In summary, using a square root simplification calculator enhances efficiency, accuracy, and understanding, making it an indispensable tool in both educational and professional settings.

Simplifying square root expressions involves breaking down the number inside the square root to its simplest form. Here are some detailed examples to illustrate this process:

Example 1: Simplify √12

First, factor 12 into its prime factors:

12 = 4 × 3

Then, apply the property of square roots:

√12 = √(4 × 3) = √4 × √3

Since the square root of 4 is 2:

√12 = 2√3

Example 2: Simplify √45

First, factor 45 into its prime factors:

45 = 9 × 5

Then, apply the property of square roots:

√45 = √(9 × 5) = √9 × √5

Since the square root of 9 is 3:

√45 = 3√5

Example 3: Simplify √72

First, factor 72 into its prime factors:

72 = 36 × 2

Then, apply the property of square roots:

√72 = √(36 × 2) = √36 × √2

Since the square root of 36 is 6:

√72 = 6√2

Example 4: Simplify √180

First, factor 180 into its prime factors:

180 = 36 × 5

Then, apply the property of square roots:

√180 = √(36 × 5) = √36 × √5

Since the square root of 36 is 6:

√180 = 6√5

Example 5: Simplify 2√12 + 9√3

First, simplify 2√12:

2√12 = 2 × 2√3 = 4√3

Now, both terms have √3, so we can add them:

4√3 + 9√3 = (4+9)√3 = 13√3

Example 6: Simplify √8

First, factor 8 into its prime factors:

8 = 4 × 2

Then, apply the property of square roots:

√8 = √(4 × 2) = √4 × √2

Since the square root of 4 is 2:

√8 = 2√2

Example 7: Simplify √50

First, factor 50 into its prime factors:

50 = 25 × 2

Then, apply the property of square roots:

√50 = √(25 × 2) = √25 × √2

Since the square root of 25 is 5:

√50 = 5√2

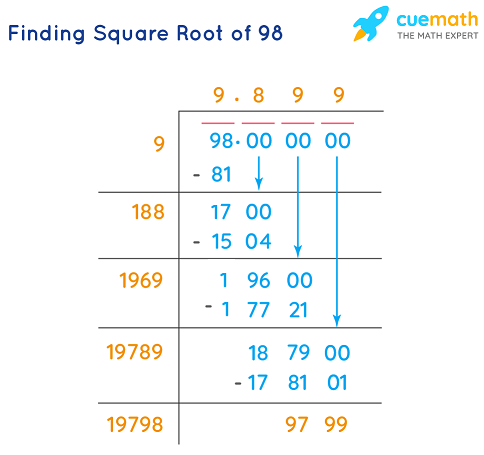
Example 8: Simplify √98

First, factor 98 into its prime factors:

98 = 49 × 2

Then, apply the property of square roots:

√98 = √(49 × 2) = √49 × √2

Since the square root of 49 is 7:

√98 = 7√2

By following these steps, you can simplify any square root expression to its simplest form.

Simplifying square root expressions can be tricky, and there are several common mistakes that students often make. Being aware of these pitfalls can help you avoid them and simplify expressions accurately.

• Forgetting to Check for Perfect Squares: Always look for perfect square factors in the number under the square root. For instance, when simplifying $\backslash (\backslash sqrt\{72\}\backslash ),\; recognize\; that\; 72\; =\; 36\; *\; 2,\; and\; thus$ \backslash (\backslash sqrt\{72\}\; =\; \backslash sqrt\{36\; \backslash times\; 2\}\; =\; 6\backslash sqrt\{2\}\backslash ).$$
• Incorrectly Applying the Product Rule: The product rule states that $\backslash (\backslash sqrt\{a\; \backslash times\; b\}\; =\; \backslash sqrt\{a\}\; \backslash times\; \backslash sqrt\{b\}\backslash )$. Ensure you apply this rule correctly. For example, $\backslash (\backslash sqrt\{50\}\; =\; \backslash sqrt\{25\; \backslash times\; 2\}\; =\; \backslash sqrt\{25\}\; \backslash times\; \backslash sqrt\{2\}\; =\; 5\backslash sqrt\{2\}\backslash ).$
• Misinterpreting the Square Root Symbol: Remember that the square root of a number has both a positive and negative value. If $\backslash (x^2\; =\; 9\backslash ),$ then $\backslash (x\; =\; 3\backslash )$ or $\backslash (x\; =\; -3\backslash ).$ Don't forget to include both solutions.
• Errors with Rationalizing the Denominator: When rationalizing denominators, multiply both the numerator and the denominator by a suitable value to eliminate the square root from the denominator. For instance, to rationalize $\backslash (\backslash frac\{\backslash sqrt\{5\}\}\{\backslash sqrt\{2\}\}\backslash ),$ multiply by $\backslash (\backslash frac\{\backslash sqrt\{2\}\}\{\backslash sqrt\{2\}\}\backslash )\; to\; get$ \backslash (\backslash frac\{\backslash sqrt\{10\}\}\{2\}\backslash ).$$
• Not Simplifying Completely: Ensure that you simplify square root expressions fully. For example, $\backslash (\backslash sqrt\{18\}\backslash )\; should\; be\; simplified\; to$ \backslash (3\backslash sqrt\{2\}\backslash )$,\; not\; left\; as$ \backslash (\backslash sqrt\{18\}\backslash ).$$
• Incorrectly Combining Terms: Only like terms can be combined. For example, $\backslash (2\backslash sqrt\{3\}\; +\; 3\backslash sqrt\{3\}\; =\; 5\backslash sqrt\{3\}\backslash ),$ but $\backslash (2\backslash sqrt\{3\}\; +\; 3\backslash sqrt\{2\}\backslash )\; cannot\; be\; combined.$

By being mindful of these common mistakes, you can improve your skills in simplifying square root expressions and achieve more accurate results.

Advanced simplification techniques for square root expressions involve a deeper understanding of algebraic rules and properties. These techniques are particularly useful when dealing with more complex expressions, including those with variables and higher-order roots.

1. Rationalizing the Denominator

When a square root appears in the denominator of a fraction, it is often useful to rationalize the denominator. This involves eliminating the square root by multiplying both the numerator and the denominator by a suitable radical.

• Example: Simplify \(\frac{1}{\sqrt{2}}\).
• Multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\): \(\frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}\).

2. Using the Product Rule

The product rule for square roots states that the square root of a product is equal to the product of the square roots of each factor.

• Example: Simplify \(\sqrt{50}\).
• Factor \(50\) into \(25 \cdot 2\).
• Apply the product rule: \(\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\).

3. Using the Quotient Rule

The quotient rule for square roots states that the square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator.

• Example: Simplify \(\sqrt{\frac{49}{4}}\).
• Apply the quotient rule: \(\sqrt{\frac{49}{4}} = \frac{\sqrt{49}}{\sqrt{4}} = \frac{7}{2}\).

4. Simplifying Higher-Order Roots

For expressions involving higher-order roots, such as cube roots or fourth roots, similar principles apply but with adjustments for the specific root.

• Example: Simplify \(\sqrt[4]{16y^4}\).
• Express as a product of fourth powers: \(\sqrt[4]{16y^4} = \sqrt[4]{(2^4)(y^4)}\).
• Simplify: \(\sqrt[4]{2^4} \cdot \sqrt[4]{y^4} = 2|y| = 2y\) (assuming \(y\) is non-negative).

5. Combining Radicals

When combining multiple radical expressions, use the product and quotient rules to simplify them into a single radical where possible.

• Example: Simplify \(\sqrt{12} \cdot \sqrt{3}\).
• Combine into one radical: \(\sqrt{12} \cdot \sqrt{3} = \sqrt{12 \cdot 3} = \sqrt{36} = 6\).

These advanced techniques require practice and a strong understanding of algebraic properties. By mastering these methods, you can efficiently simplify even the most complex square root expressions.

Simplifying square root expressions has various applications in real-world scenarios. Understanding these applications can help you appreciate the practical significance of mastering this skill. Here are some examples:

• Construction and Architecture

  When designing buildings and other structures, architects and engineers often use the Pythagorean Theorem, which involves square roots, to calculate dimensions. For instance, determining the length of a diagonal brace in a rectangular frame requires the square root of the sum of the squares of the other two sides.

  Example:

  Problem:	Find the diagonal length of a rectangular wall with sides 8 ft and 15 ft.
  Solution:	\(\sqrt{8^2 + 15^2} = \sqrt{64 + 225} = \sqrt{289} = 17 \text{ ft}\)

• Physics and Engineering

  In physics, calculating distances, velocities, and other vector quantities often involves square roots. For example, the distance between two points in space can be determined using the distance formula, which is derived from the Pythagorean Theorem.

  Example:

  Problem:	Calculate the distance between points (3, 4) and (7, 1).
  Solution:	\(\sqrt{(7-3)^2 + (1-4)^2} = \sqrt{4^2 + (-3)^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \text{ units}\)

• Astronomy

  In astronomy, the distances between celestial bodies are often calculated using methods that involve square roots. For instance, the parallax method for measuring the distance to stars involves the square root of the sum of squared distances.

• Navigation

  GPS and other navigation systems use algorithms that involve square roots to calculate the shortest path between two points on the Earth’s surface.

• Economics and Finance

  Square roots are used in finance to calculate standard deviation and other risk metrics, which are crucial for portfolio management and investment strategies.

These examples demonstrate the wide-ranging applications of simplifying square root expressions in various fields, emphasizing the importance of this mathematical skill.