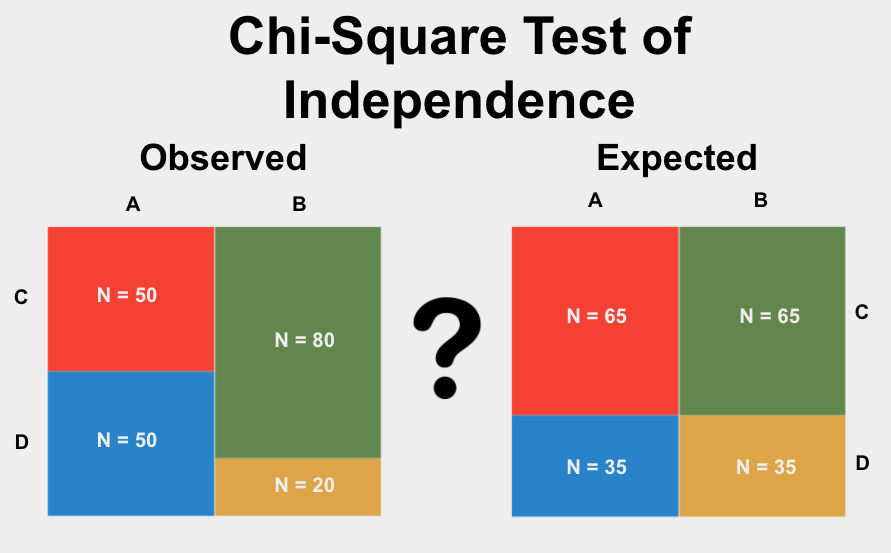
Topic examples of chi square test problems: Understanding chi-square test problems is essential for analyzing categorical data and determining relationships between variables. This article provides various examples of chi-square test problems, guiding you through different scenarios and types of chi-square tests. Whether you're dealing with goodness of fit or independence tests, these examples will help clarify the application and interpretation of chi-square tests in statistical analysis.
Table of Content
- Chi-Square Test for Independence
- Chi-Square Goodness of Fit Test
- Steps to Perform a Chi-Square Test
- Chi-Square Goodness of Fit Test
- Steps to Perform a Chi-Square Test
- Steps to Perform a Chi-Square Test
- Introduction to Chi-Square Test
- Types of Chi-Square Tests
- Chi-Square Test of Independence
- Hypothesis Testing Using Chi-Square Test
- Step-by-Step Guide to Performing Chi-Square Test
- Formulas and Calculations
- Examples of Chi-Square Test Problems
- Practice Questions and Solutions
- Frequently Asked Questions
- YOUTUBE:
Chi-Square Test for Independence
This test evaluates if two categorical variables are independent of each other.
Example
A researcher wants to know if there is an association between gender (male, female) and preference for a new product (like, dislike).
- Null Hypothesis (\(H_0\)): Gender and product preference are independent.
- Alternative Hypothesis (\(H_a\)): Gender and product preference are not independent.
- Observed Frequencies:
Like Dislike Male 30 20 Female 25 25 - Expected Frequencies:
Like Dislike Male 27.5 22.5 Female 27.5 22.5 - Chi-Square Statistic: \[ \chi^2 = \sum \frac{(O - E)^2}{E} = \frac{(30-27.5)^2}{27.5} + \frac{(20-22.5)^2}{22.5} + \frac{(25-27.5)^2}{27.5} + \frac{(25-22.5)^2}{22.5} = 0.227 \]

READ MORE:
Chi-Square Goodness of Fit Test
This test determines if the sample data matches an expected distribution.
Example
A dog food company tests three new flavors: Garlic Blast, Blueberry Delight, and Minty Munch. They expect equal preference among 75 dogs.
- Null Hypothesis (\(H_0\)): Dogs show no preference for any flavor.
- Alternative Hypothesis (\(H_a\)): Dogs show a preference for at least one flavor.
- Observed Frequencies:
Flavor Observed Expected Garlic Blast 22 25 Blueberry Delight 30 25 Minty Munch 23 25 - Chi-Square Statistic: \[ \chi^2 = \sum \frac{(O - E)^2}{E} = \frac{(22-25)^2}{25} + \frac{(30-25)^2}{25} + \frac{(23-25)^2}{25} = 1.24 \]
Steps to Perform a Chi-Square Test
- State the hypotheses.
- Construct a contingency table of observed frequencies.
- Calculate the expected frequencies.
- Compute the chi-square statistic using the formula: \[ \chi^2 = \sum \frac{(O - E)^2}{E} \]
- Determine the degrees of freedom (\(df\)): \[ df = (r - 1) \times (c - 1) \] where \(r\) is the number of rows and \(c\) is the number of columns.
- Compare the chi-square statistic to the critical value from the chi-square distribution table.
- Make a decision to reject or fail to reject the null hypothesis.
Chi-Square Goodness of Fit Test
This test determines if the sample data matches an expected distribution.
Example
A dog food company tests three new flavors: Garlic Blast, Blueberry Delight, and Minty Munch. They expect equal preference among 75 dogs.
- Null Hypothesis (\(H_0\)): Dogs show no preference for any flavor.
- Alternative Hypothesis (\(H_a\)): Dogs show a preference for at least one flavor.
- Observed Frequencies:
Flavor Observed Expected Garlic Blast 22 25 Blueberry Delight 30 25 Minty Munch 23 25 - Chi-Square Statistic: \[ \chi^2 = \sum \frac{(O - E)^2}{E} = \frac{(22-25)^2}{25} + \frac{(30-25)^2}{25} + \frac{(23-25)^2}{25} = 1.24 \]
Steps to Perform a Chi-Square Test
- State the hypotheses.
- Construct a contingency table of observed frequencies.
- Calculate the expected frequencies.
- Compute the chi-square statistic using the formula: \[ \chi^2 = \sum \frac{(O - E)^2}{E} \]
- Determine the degrees of freedom (\(df\)): \[ df = (r - 1) \times (c - 1) \] where \(r\) is the number of rows and \(c\) is the number of columns.
- Compare the chi-square statistic to the critical value from the chi-square distribution table.
- Make a decision to reject or fail to reject the null hypothesis.

Steps to Perform a Chi-Square Test
- State the hypotheses.
- Construct a contingency table of observed frequencies.
- Calculate the expected frequencies.
- Compute the chi-square statistic using the formula: \[ \chi^2 = \sum \frac{(O - E)^2}{E} \]
- Determine the degrees of freedom (\(df\)): \[ df = (r - 1) \times (c - 1) \] where \(r\) is the number of rows and \(c\) is the number of columns.
- Compare the chi-square statistic to the critical value from the chi-square distribution table.
- Make a decision to reject or fail to reject the null hypothesis.
Introduction to Chi-Square Test
The Chi-Square test is a statistical method developed by Karl Pearson in 1900. It is used to determine if there is a significant association between two categorical variables. This test is widely applied in fields like social sciences, market research, and genetics to analyze the relationship between observed and expected frequencies in data.
The formula for the Chi-Square statistic is:
\[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \]
Where:
- \( O_i \) = Observed frequency
- \( E_i \) = Expected frequency, calculated as: \[ E = \frac{(\text{Row Total} \times \text{Column Total})}{\text{Grand Total}} \]
The Chi-Square test can be used in different contexts:
- Test of Independence: Determines if there is a significant association between two categorical variables.
- Test of Goodness of Fit: Assesses if sample data matches a population with a specific distribution.
Steps to perform a Chi-Square Test:
- State the Hypotheses:
- Null Hypothesis (\(H_0\)): Assumes no association between the variables.
- Alternative Hypothesis (\(H_1\)): Assumes an association between the variables.
- Calculate the Expected Frequencies: Using the formula mentioned above.
- Compute the Chi-Square Statistic: Use the Chi-Square formula to calculate the test statistic.
- Determine the Degrees of Freedom: \[ df = (r-1)(c-1) \] where \(r\) is the number of rows and \(c\) is the number of columns.
- Compare the Test Statistic to the Critical Value: Use a Chi-Square distribution table to find the critical value at a desired significance level (\(\alpha\)).
- Make a Decision: If the Chi-Square statistic is greater than the critical value, reject the null hypothesis. Otherwise, fail to reject the null hypothesis.
In conclusion, the Chi-Square test is a versatile statistical tool used to test relationships between categorical variables, helping researchers understand the structure and patterns within their data.
Types of Chi-Square Tests
The Chi-Square test is a statistical method to determine if there is a significant association between two categorical variables. There are mainly two types of Chi-Square tests:
-
Chi-Square Test of Independence
This test determines whether there is a significant association between two categorical variables. For example, it can be used to test if there is an association between gender and political party preference. The null hypothesis (\(H_0\)) states that there is no association between the variables, while the alternative hypothesis (\(H_1\)) states that there is an association.
Steps to perform Chi-Square Test of Independence:
- Formulate the hypotheses.
- Create a contingency table of the observed frequencies.
- Calculate the expected frequencies using the formula: \(Expected\ Value = \frac{(Row\ Total) \times (Column\ Total)}{Total\ Number\ of\ Observations}\)
- Compute the Chi-Square statistic using: \(X^2 = \sum \frac{(O_i - E_i)^2}{E_i}\)
- Compare the calculated \(X^2\) value with the critical value from the Chi-Square distribution table.
- Draw a conclusion to accept or reject the null hypothesis.
-
Chi-Square Goodness of Fit Test
This test assesses how well the observed distribution of a single categorical variable fits an expected distribution. For example, it can be used to test if the preference for different dog food flavors is as expected. The null hypothesis (\(H_0\)) states that the observed frequencies match the expected frequencies, while the alternative hypothesis (\(H_1\)) states that they do not match.
Steps to perform Chi-Square Goodness of Fit Test:
- Formulate the hypotheses.
- Determine the expected frequencies for each category.
- Calculate the Chi-Square statistic using: \(X^2 = \sum \frac{(O_i - E_i)^2}{E_i}\)
- Compare the calculated \(X^2\) value with the critical value from the Chi-Square distribution table.
- Draw a conclusion to accept or reject the null hypothesis.
Chi-Square Test of Independence
The Chi-Square Test of Independence is a statistical method used to determine whether two categorical variables are independent of each other. This test is useful when you want to explore the relationship between two variables in a contingency table, which displays the frequency distribution of the variables.
Here are the steps involved in conducting a Chi-Square Test of Independence:
-
State the Hypotheses:
- Null Hypothesis (H0): The two variables are independent.
- Alternative Hypothesis (H1): The two variables are dependent.
-
Calculate the Expected Frequencies:
For each cell in the contingency table, the expected frequency is calculated using the formula:
\[ E = \frac{\text{Row Total} \times \text{Column Total}}{\text{Grand Total}} \] -
Compute the Chi-Square Statistic:
The Chi-Square statistic is computed using the formula:
\[ \chi^2 = \sum \frac{(O - E)^2}{E} \]where \( O \) represents the observed frequency and \( E \) represents the expected frequency.
-
Determine the Degrees of Freedom:
The degrees of freedom for the test are calculated as:
\[ \text{Degrees of Freedom} = (r - 1) \times (c - 1) \]where \( r \) is the number of rows and \( c \) is the number of columns in the contingency table.
-
Compare the Chi-Square Statistic to the Critical Value:
Using a Chi-Square distribution table, compare the computed Chi-Square statistic to the critical value based on the degrees of freedom and the chosen significance level (e.g., 0.05).
- If \( \chi^2 \) is greater than the critical value, reject the null hypothesis.
- If \( \chi^2 \) is less than or equal to the critical value, do not reject the null hypothesis.
The Chi-Square Test of Independence is a powerful tool for determining relationships between categorical variables, making it widely used in fields such as market research, health sciences, and social sciences.
Hypothesis Testing Using Chi-Square Test
The Chi-Square test is a statistical method used to determine if there is a significant association between two categorical variables. It is commonly used in hypothesis testing. Here, we will explain the step-by-step process to perform a Chi-Square test for independence.
Steps to Perform a Chi-Square Test
-
State the Hypotheses:
- Null Hypothesis (\( H_0 \)): Assumes that there is no association between the two categorical variables.
- Alternative Hypothesis (\( H_1 \)): Assumes that there is an association between the two categorical variables.
-
Construct the Contingency Table:
Organize the observed data into a table format with rows and columns representing the categories of the two variables.
Category 1 Category 2 Total Row 1 Observed Value Observed Value Row Total Row 2 Observed Value Observed Value Row Total Total Column Total Column Total Grand Total -
Calculate the Expected Frequencies:
Use the formula to calculate the expected frequency for each cell in the contingency table:
\[ E_{ij} = \frac{(Row \ Total \times Column \ Total)}{Grand \ Total} \]
-
Compute the Chi-Square Statistic:
For each cell, calculate the Chi-Square statistic using the formula:
\[ \chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \]
Where \( O_{ij} \) is the observed frequency and \( E_{ij} \) is the expected frequency.
-
Determine the Degrees of Freedom:
The degrees of freedom for the Chi-Square test is calculated as:
\[ df = (r - 1) \times (c - 1) \]
Where \( r \) is the number of rows and \( c \) is the number of columns in the contingency table.
-
Compare the Chi-Square Statistic to the Critical Value:
Find the critical value from the Chi-Square distribution table using the calculated degrees of freedom and the chosen significance level (e.g., 0.05). Compare the calculated Chi-Square statistic to the critical value.
- If \( \chi^2 \) is greater than the critical value, reject the null hypothesis.
- If \( \chi^2 \) is less than or equal to the critical value, fail to reject the null hypothesis.
-
Make a Decision:
Based on the comparison, conclude whether there is sufficient evidence to suggest an association between the variables.
Example Problem
Suppose we want to test if there is an association between gender (male, female) and political party preference (Republican, Democrat, Independent). We collect data from a sample of voters and summarize the observed frequencies in a contingency table.
| Republican | Democrat | Independent | Total | |
|---|---|---|---|---|
| Male | 100 | 70 | 30 | 200 |
| Female | 140 | 60 | 20 | 220 |
| Total | 240 | 130 | 50 | 420 |
We then calculate the expected frequencies, compute the Chi-Square statistic, determine the degrees of freedom, and compare the Chi-Square statistic to the critical value to make a decision on the hypothesis.
Step-by-Step Guide to Performing Chi-Square Test
The Chi-Square test is a statistical method used to determine if there is a significant association between categorical variables. Here, we will provide a detailed, step-by-step guide to performing a Chi-Square test.
1. Formulate the Hypotheses
Start by formulating the null hypothesis (\(H_0\)) and the alternative hypothesis (\(H_1\)).
- Null Hypothesis (\(H_0\)): There is no association between the variables (they are independent).
- Alternative Hypothesis (\(H_1\)): There is an association between the variables (they are dependent).
2. Create a Contingency Table
Organize the observed frequencies of the data into a contingency table. This table shows the distribution of variables.
| Category | Variable 1 | Variable 2 | Row Total |
|---|---|---|---|
| Group 1 | O11 | O12 | R1 |
| Group 2 | O21 | O22 | R2 |
| Column Total | C1 | C2 | n |
3. Calculate Expected Frequencies
Calculate the expected frequencies using the formula:
\[ E_{ij} = \frac{(R_i \times C_j)}{n} \]
where:
- \(E_{ij}\) = Expected frequency for cell (i, j)
- \(R_i\) = Total for row i
- \(C_j\) = Total for column j
- \(n\) = Grand total of all observations
4. Compute the Chi-Square Statistic
Calculate the Chi-Square statistic using the formula:
\[ \chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \]
where:
- \(O_{ij}\) = Observed frequency for cell (i, j)
- \(E_{ij}\) = Expected frequency for cell (i, j)
5. Determine the Degrees of Freedom
The degrees of freedom (df) for the Chi-Square test is calculated as:
\[ df = (r - 1) \times (c - 1) \]
where:
- \(r\) = Number of rows
- \(c\) = Number of columns
6. Find the Critical Value
Using a Chi-Square distribution table, find the critical value based on the degrees of freedom and the desired significance level (α, usually 0.05).
7. Make a Decision
Compare the calculated Chi-Square statistic to the critical value:
- If \(\chi^2\) calculated > \(\chi^2\) critical, reject the null hypothesis (\(H_0\)).
- If \(\chi^2\) calculated ≤ \(\chi^2\) critical, do not reject the null hypothesis (\(H_0\)).
By following these steps, you can effectively perform a Chi-Square test to determine if there is a significant association between categorical variables.
Formulas and Calculations
The chi-square test is a statistical method used to determine if there is a significant association between categorical variables. There are two main types of chi-square tests: the chi-square goodness of fit test and the chi-square test of independence. Both tests use the same fundamental formula.
Chi-Square Test Formula
The chi-square statistic is calculated using the formula:
\[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \]
Where:
- \(\chi^2\) is the chi-square test statistic
- \(O_i\) is the observed frequency
- \(E_i\) is the expected frequency
- \(\sum\) denotes the sum over all categories
Calculating Expected Frequencies
To calculate the expected frequencies (\(E_i\)) for each category, use the formula:
\[ E_i = \frac{( \text{Row Total} \times \text{Column Total} )}{\text{Grand Total}} \]
For example, consider a table showing the distribution of gender (male and female) across different political party preferences (Republican, Democrat, Independent):
| Republican | Democrat | Independent | Total | |
|---|---|---|---|---|
| Male | 100 | 70 | 30 | 200 |
| Female | 140 | 60 | 20 | 220 |
| Total | 240 | 130 | 50 | 420 |
The expected frequency for males preferring Republicans is calculated as:
\[ E = \frac{(200 \times 240)}{440} = 109.09 \]
Similarly, calculate the expected frequencies for all cells in the contingency table.
Calculating the Chi-Square Statistic
Using the observed (\(O_i\)) and expected (\(E_i\)) frequencies, apply the chi-square formula to each cell and sum the results:
\[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \]
For example, for the cell with males preferring Republicans:
\[ \chi^2 = \frac{(100 - 109.09)^2}{109.09} = 0.756 \]
Repeat this calculation for each cell and sum all the values to obtain the final chi-square statistic.
Degrees of Freedom
The degrees of freedom (df) for the chi-square test is calculated as:
\[ df = (r - 1) \times (c - 1) \]
where \(r\) is the number of rows and \(c\) is the number of columns. In our example:
\[ df = (2 - 1) \times (3 - 1) = 2 \]
Interpreting the Result
Compare the calculated chi-square statistic to the critical value from the chi-square distribution table at a chosen significance level (e.g., 0.05). If the chi-square statistic exceeds the critical value, reject the null hypothesis.
This process helps to determine whether there is a significant association between the categorical variables being studied.
Examples of Chi-Square Test Problems
The Chi-Square test is a statistical method to determine if there is a significant association between categorical variables. Here are some detailed examples of Chi-Square test problems:
Example 1: Chi-Square Test of Independence
Suppose we want to investigate if there is an association between gender and political party preference. A survey is conducted with the following results:
| Political Party | Male | Female | Total |
|---|---|---|---|
| Republican | 100 | 140 | 240 |
| Democrat | 70 | 60 | 130 |
| Independent | 30 | 20 | 50 |
| Total | 200 | 220 | 440 |
To test the independence between gender and political party preference, follow these steps:
- Define Hypotheses:
- Null Hypothesis (\(H_0\)): There is no association between gender and political party preference.
- Alternative Hypothesis (\(H_1\)): There is an association between gender and political party preference.
- Calculate Expected Frequencies:
Use the formula: \[ \text{Expected Frequency} = \frac{\text{(Row Total)} \times \text{(Column Total)}}{\text{Grand Total}} \]Political Party Male Female Republican \(\frac{240 \times 200}{440} = 109.09\) \(\frac{240 \times 220}{440} = 120.91\) Democrat \(\frac{130 \times 200}{440} = 59.09\) \(\frac{130 \times 220}{440} = 70.91\) Independent \(\frac{50 \times 200}{440} = 22.73\) \(\frac{50 \times 220}{440} = 27.27\) - Calculate Chi-Square Statistic:
Use the formula: \[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \]
Sum of values: \( \chi^2 = 9.837 \)Political Party Male Female Republican 0.743 3.333 Democrat 2.051 0.385 Independent 2.333 1.000 - Determine Degrees of Freedom (df):
\[ \text{df} = (\text{number of rows} - 1) \times (\text{number of columns} - 1) = (3 - 1) \times (2 - 1) = 2 \] - Find the Critical Value:
For \( \alpha = 0.05 \) and \( df = 2 \), the critical value from the chi-square table is 5.991. - Compare and Conclude:
Since \( \chi^2 = 9.837 \) is greater than 5.991, we reject the null hypothesis and conclude that there is a significant association between gender and political party preference.
Example 2: Chi-Square Goodness of Fit Test
Suppose we want to test if a die is fair. We roll the die 60 times and observe the following frequencies:
| Face | Observed Frequency |
|---|---|
| 1 | 10 |
| 2 | 9 |
| 3 | 11 |
| 4 | 8 |
| 5 | 12 |
| 6 | 10 |
To test the fairness of the die, follow these steps:
- Define Hypotheses:
- Null Hypothesis (\(H_0\)): The die is fair (each face has an equal probability of 1/6).
- Alternative Hypothesis (\(H_1\)): The die is not fair.
- Calculate Expected Frequencies:
Since the die is fair, the expected frequency for each face is: \[ E = \frac{60}{6} = 10 \] - Calculate Chi-Square Statistic:
Use the formula: \[ \chi^2 = \sum \frac{(O_i - E_i)^2}{E_i} \] \[ \chi^2 = \frac{(10-10)^2}{10} + \frac{(9-10)^2}{10} + \frac{(11-10)^2}{10} + \frac{(8-10)^2}{10} + \frac{(12-10)^2}{10} + \frac{(10-10)^2}{10} = 0 + 0.1 + 0.1 + 0.4 + 0.4 + 0 = 1.0 \] - Determine Degrees of Freedom (df):
\[ \text{df} = \text{number of categories} - 1 = 6 - 1 = 5 \] - Find the Critical Value:
For \( \alpha = 0.05 \) and \( df = 5 \), the critical value from the chi-square table is 11.07. - Compare and Conclude:
Since \( \chi^2 = 1.0 \) is less than 11.07, we fail to reject the null hypothesis and conclude that there is no significant evidence to suggest that the die is not fair.

Practice Questions and Solutions
Here are some practice questions to help you understand and apply the Chi-Square test. Each question includes a detailed solution to guide you through the process.
Question 1: Chi-Square Goodness of Fit Test
A biologist claims that an equal number of four different species of deer enter a certain wooded area in a forest each week. To test this hypothesis, she records the number of each species of deer that enter the wooded area over the course of one week:
- Species 1: 22
- Species 2: 20
- Species 3: 23
- Species 4: 35
Conduct a Chi-Square Goodness of Fit Test to determine if the distribution of the deer species is consistent with the hypothesized distribution.
Solution:
- State the null hypothesis (\(H_0\)): The distribution of the deer species is as hypothesized.
- Calculate the expected frequencies for each category assuming the null hypothesis is true.
- Calculate the Chi-Square statistic:
Species Observed (O) Expected (E) \((O-E)^2/E\) Species 1 22 25 \(\frac{(22-25)^2}{25} = 0.36\) Species 2 20 25 \(\frac{(20-25)^2}{25} = 1.00\) Species 3 23 25 \(\frac{(23-25)^2}{25} = 0.16\) Species 4 35 25 \(\frac{(35-25)^2}{25} = 4.00\) - Sum the last column to get the Chi-Square statistic: \(0.36 + 1.00 + 0.16 + 4.00 = 5.52\).
- Compare the Chi-Square statistic to the critical value from the Chi-Square distribution table with 3 degrees of freedom at a significance level of 0.05 (critical value = 7.815).
- Decision: Since 5.52 < 7.815, we do not reject the null hypothesis.
- Conclusion: There is no significant evidence to suggest that the true distribution of deer species is different from the hypothesized distribution.
Question 2: Chi-Square Test of Independence
A researcher wants to know whether marital status is associated with education level. A random sample of 300 individuals is surveyed, and the following data is obtained:
| High School | Bachelor’s | Master’s or Higher | Total | |
|---|---|---|---|---|
| Married | 20 | 100 | 35 | 155 |
| Single | 50 | 80 | 15 | 145 |
| Total | 70 | 180 | 50 | 300 |
Use a Chi-Square Test of Independence to determine if there is a significant association between marital status and education level.
Solution:
- State the null hypothesis (\(H_0\)): Marital status and education level are independent.
- Calculate the expected frequencies for each cell:
High School Bachelor’s Master’s or Higher Total Married \(\frac{155 \times 70}{300} = 36.17\) \(\frac{155 \times 180}{300} = 93.00\) \(\frac{155 \times 50}{300} = 25.83\) 155 Single \(\frac{145 \times 70}{300} = 33.83\) \(\frac{145 \times 180}{300} = 87.00\) \(\frac{145 \times 50}{300} = 24.17\) 145 Total 70 180 50 300 - Calculate the Chi-Square statistic: \[ \chi^2 = \sum \frac{(O-E)^2}{E} = \frac{(20-36.17)^2}{36.17} + \frac{(100-93)^2}{93} + \cdots + \frac{(15-24.17)^2}{24.17} = 24.10 \]
- Compare the Chi-Square statistic to the critical value from the Chi-Square distribution table with 2 degrees of freedom at a significance level of 0.05 (critical value = 5.991).
- Decision: Since 24.10 > 5.991, we reject the null hypothesis.
- Conclusion: There is a significant association between marital status and education level.
Frequently Asked Questions
Here are some frequently asked questions about the Chi-Square test:
-
What is a Chi-Square test?
The Chi-Square test is a statistical method used to determine if there is a significant association between categorical variables. It compares the observed frequencies in each category with the frequencies that would be expected if there were no association between the variables.
-
When should I use a Chi-Square test?
You should use a Chi-Square test when you want to test the relationship between two categorical variables. This includes situations like testing the independence of variables or the goodness-of-fit to a specified distribution.
-
How do I calculate the expected frequencies in a Chi-Square test?
The expected frequency for each category is calculated using the formula:
\[
E = \frac{(\text{Row Total}) \times (\text{Column Total})}{\text{Grand Total}}
\]where the row total is the total number of observations in the row, the column total is the total number of observations in the column, and the grand total is the total number of observations overall.
-
What is the formula for the Chi-Square statistic?
The Chi-Square statistic is calculated using the formula:
\[
\chi^2 = \sum \frac{(O - E)^2}{E}
\]where \(O\) is the observed frequency and \(E\) is the expected frequency.
-
How do I interpret the Chi-Square statistic?
The Chi-Square statistic is compared to a critical value from the Chi-Square distribution table, based on the degrees of freedom and the significance level. If the Chi-Square statistic is greater than the critical value, you reject the null hypothesis and conclude that there is a significant association between the variables.
-
What are degrees of freedom in a Chi-Square test?
The degrees of freedom (df) in a Chi-Square test are calculated as:
\[
df = (r - 1) \times (c - 1)
\]where \(r\) is the number of rows and \(c\) is the number of columns in the contingency table.
-
What are the assumptions of the Chi-Square test?
- The data should be in the form of frequencies or counts of cases.
- The categories are mutually exclusive.
- Each observation should appear in only one category.
- The sample size should be sufficiently large, generally at least 5 observations per category.
-
What are the types of Chi-Square tests?
There are two main types of Chi-Square tests:
- Chi-Square Goodness-of-Fit Test: This test determines if a sample data matches a population with a specific distribution.
- Chi-Square Test of Independence: This test evaluates whether two categorical variables are independent of each other.
-
Can the Chi-Square test be used for small samples?
The Chi-Square test is not reliable for very small sample sizes. For small samples, Fisher's Exact Test is often recommended as an alternative.
-
What is a contingency table?
A contingency table (or cross-tabulation) is a table used in statistics to show the frequency distribution of variables. It helps in calculating the Chi-Square statistic for tests of independence.
Kiểm Định Chi-Square
READ MORE:
Cách... Thực Hiện Kiểm Định Chi-Square (Bằng Tay)


:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)