X Squared Plus Y Squared: A Comprehensive Guide to Understanding Its Significance

The equation \( x^2 + y^2 \) is fundamental in various mathematical contexts. Here, we explore its significance in geometry and algebra.

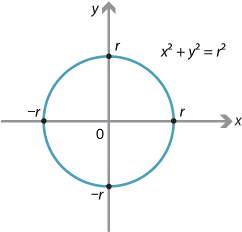
Circle Equation

In geometry, the equation \( x^2 + y^2 = r^2 \) represents a circle with its center at the origin (0,0) and radius \( r \). For example, the equation \( x^2 + y^2 = 25 \) describes a circle with a radius of 5 units.

Geometric Interpretation

• Center: (0, 0)
• Radius: \( \sqrt{25} = 5 \)

Graphical Representation

The circle can be visualized on a coordinate plane, with every point \( (x, y) \) on the circle satisfying the equation \( x^2 + y^2 = 25 \).

Simplification of \( \sqrt{x^2 + y^2} \)

Simplifying the expression \( \sqrt{x^2 + y^2} \) can be complex. While it may seem straightforward to cancel the squares with the square root, this is not the case when two terms are involved. The expression can be simplified using polar coordinates, where \( x^2 + y^2 = r^2 \), thus \( \sqrt{x^2 + y^2} = r \).

Conversion to Polar Coordinates

In polar coordinates, the relationship is expressed as:

\( r = \sqrt{x^2 + y^2} \)

Where \( r \) is the radius, which simplifies the original expression to \( r \) in this coordinate system.

Key Points

• The equation \( x^2 + y^2 = r^2 \) represents a circle.
• The expression \( \sqrt{x^2 + y^2} \) can be interpreted as the radius in polar coordinates.
• Direct simplification of \( \sqrt{x^2 + y^2} \) without converting to polar coordinates is not feasible.

The expression \( x^2 + y^2 \) is fundamental in mathematics, appearing in various contexts such as geometry, algebra, and calculus. It represents the sum of the squares of two variables, often used in the Pythagorean theorem to determine distances and in equations of circles.

In the Cartesian coordinate system, the equation \( x^2 + y^2 = r^2 \) defines a circle centered at the origin with radius \( r \). This form is crucial in graphing and analyzing circular shapes in both two-dimensional and three-dimensional spaces.

Another important application of \( x^2 + y^2 \) is in simplifying expressions involving radicals. While the square root of the sum of squares \( \sqrt{x^2 + y^2} \) cannot be simplified algebraically in most cases, it can be expressed in polar coordinates as \( r \), where \( r \) is the radius of a circle centered at the origin.

Here are some key points about \( x^2 + y^2 \):

• It is used in the Pythagorean theorem: \( a^2 + b^2 = c^2 \), where \( c \) is the hypotenuse of a right triangle.
• It defines the equation of a circle: \( x^2 + y^2 = r^2 \).
• In polar coordinates, \( x^2 + y^2 = r^2 \) simplifies to \( r \), which represents the distance from the origin.

Overall, the expression \( x^2 + y^2 \) is a cornerstone in mathematical problem-solving, offering insights into geometric shapes, distances, and algebraic simplifications.

The expression \( x^2 + y^2 \) has numerous applications in geometry, ranging from defining basic shapes to complex geometric properties. Here are some of the key applications:

• Equation of a Circle:

  The most common application is in the equation of a circle. The general form of the equation is \((x - a)^2 + (y - b)^2 = r^2\), where \((a, b)\) is the center of the circle and \(r\) is the radius. This equation represents all the points \((x, y)\) that are at a distance \(r\) from the center.

• Distance Formula:

  The formula \( x^2 + y^2 \) can be used to calculate the distance between two points in a coordinate plane. For points \((x_1, y_1)\) and \((x_2, y_2)\), the distance \(d\) is given by \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \), which is derived from the Pythagorean theorem.

• Ellipses and Hyperbolas:

  In the study of conic sections, the equation \( x^2 + y^2 \) helps in defining ellipses and hyperbolas. For instance, an ellipse with axes aligned with the coordinate axes can be represented as \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \), where \(a\) and \(b\) are the semi-major and semi-minor axes, respectively.

• Vector Magnitude:

  In vector geometry, the magnitude of a vector \(\vec{v} = (x, y)\) is given by \( \|\vec{v}\| = \sqrt{x^2 + y^2} \). This is essential in physics and engineering for determining the length and direction of vectors.

• Polar Coordinates:

  The conversion between Cartesian and polar coordinates involves \( x^2 + y^2 \). For a point with polar coordinates \((r, \theta)\), the Cartesian coordinates are \( x = r \cos \theta \) and \( y = r \sin \theta \), with \( r = \sqrt{x^2 + y^2} \).

The equation \( x^2 + y^2 = r^2 \) represents a circle with its center at the origin \((0,0)\) and radius \( r \). This is known as the standard form of a circle's equation.

Here's a step-by-step explanation of this equation:

1. Understanding the Equation:

   In the equation \( x^2 + y^2 = r^2 \), \( r \) represents the radius of the circle. The values of \( x \) and \( y \) are the coordinates of any point on the circle. The sum of the squares of the \( x \) and \( y \) coordinates of any point on the circle is equal to the square of the radius.

2. Derivation Using Pythagorean Theorem:

   Consider a point \((x, y)\) on the circle. The distance from this point to the origin (the center of the circle) is the radius \( r \). According to the Pythagorean theorem in a right triangle formed by the radius, we have:
   \[ x^2 + y^2 = r^2 \]

3. Graphing the Circle:

   To graph the circle, you can plot several points that satisfy the equation \( x^2 + y^2 = r^2 \). For instance, if \( r = 2 \), the equation becomes:
   \[ x^2 + y^2 = 4 \]
   You can find points like \((2,0)\), \((0,2)\), \((-2,0)\), and \((0,-2)\) which lie on the circle.

4. Plotting Points:

   For the equation \( x^2 + y^2 = 4 \):
   \[ y^2 = 4 - x^2 \]
   Taking the square root of both sides gives:
   \[ y = \pm \sqrt{4 - x^2} \]
   By calculating the values for various \( x \) coordinates, you can plot the corresponding \( y \) coordinates to draw the circle.

To find the center and radius of a circle given its equation, we can use the standard form of a circle's equation:

\( (x - h)^2 + (y - k)^2 = r^2 \)

Here, \( (h, k) \) represents the center of the circle, and \( r \) is the radius.

Let's go through the steps to determine the center and radius:

1. Identify the given equation of the circle. For example, consider the equation:

   \( x^2 + y^2 = 25 \)

2. Compare the given equation with the standard form. In this case, the equation can be rewritten as:

   \( (x - 0)^2 + (y - 0)^2 = 25 \)

3. From this comparison, we can see that:

   • The center \((h, k)\) is \((0, 0)\).
   • The radius \( r \) is the square root of 25, which is \( 5 \).

Therefore, the center of the circle is \((0, 0)\) and the radius is \( 5 \).

Let's consider another example with a more complex equation:

\( x^2 + (y - 2)^2 = 16 \)

1. Rewrite the equation in the standard form:

   \( (x - 0)^2 + (y - 2)^2 = 4^2 \)

2. From this comparison, we can determine:

   • The center \((h, k)\) is \((0, 2)\).
   • The radius \( r \) is \( 4 \).

For an equation not in the standard form, such as:

\( x^2 + y^2 - 4y = 21 \)

1. First, complete the square for the \( y \) terms. Start by isolating the \( y \) terms:

   \( x^2 + y^2 - 4y + 4 = 21 + 4 \)

   \( x^2 + (y - 2)^2 = 25 \)

2. Now, compare with the standard form:

   • The center \((h, k)\) is \((0, 2)\).
   • The radius \( r \) is \( 5 \).

Using these methods, you can determine the center and radius for any circle given its equation.

Simplifying expressions involving \( x^2 + y^2 \) is a common task in algebra and geometry. Below are some methods to simplify and transform these expressions.

Simplifying \( \sqrt{x^2 + y^2} \)

The expression \( \sqrt{x^2 + y^2} \) represents the Euclidean distance from the origin to the point \((x, y)\) in the Cartesian coordinate system. To simplify this expression:

1. Recognize that \( \sqrt{x^2 + y^2} \) is always non-negative.
2. Use properties of square roots to break down the expression if possible.
3. In some contexts, apply trigonometric identities for further simplification.

For example:

If \( x = 3 \) and \( y = 4 \), then \( \sqrt{x^2 + y^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \).

Polar Coordinates Transformation

Transforming Cartesian coordinates \((x, y)\) to polar coordinates \((r, \theta)\) can simplify the expression \( x^2 + y^2 \). The transformation is given by:

• \( x = r \cos(\theta) \)
• \( y = r \sin(\theta) \)

Thus, \( x^2 + y^2 \) becomes:

\[
x^2 + y^2 = (r \cos(\theta))^2 + (r \sin(\theta))^2 = r^2 \cos^2(\theta) + r^2 \sin^2(\theta) = r^2 (\cos^2(\theta) + \sin^2(\theta)) = r^2
\]

Since \(\cos^2(\theta) + \sin^2(\theta) = 1\).

This transformation is particularly useful in problems involving circular symmetry.

Using Algebraic Identities

In some cases, algebraic identities can help simplify expressions involving \( x^2 + y^2 \). For instance:

• Recognize patterns such as the difference of squares: \( (x + y)^2 - 2xy = x^2 + y^2 \).
• Utilize symmetry properties: if \( x = y \), then \( x^2 + y^2 = 2x^2 \).

Application in Complex Numbers

The expression \( x^2 + y^2 \) frequently appears in the context of complex numbers. If \( z = x + yi \) is a complex number, then:

\[
|z|^2 = z \overline{z} = (x + yi)(x - yi) = x^2 + y^2
\]

Here, \(|z|\) represents the modulus of the complex number \( z \).

Example Problems

1. Simplify \( \sqrt{(3a)^2 + (4b)^2} \).
2. Convert the Cartesian coordinates (5, 12) to polar coordinates and find \( x^2 + y^2 \).
3. Given \( z = 7 + 24i \), calculate \(|z|^2\).

Each of these problems reinforces the techniques discussed and provides practice in simplifying expressions involving \( x^2 + y^2 \).

The expression \( \sqrt{x^2 + y^2} \) represents the Euclidean norm or magnitude of the vector \( (x, y) \) in a Cartesian coordinate system. It is commonly referred to as the distance from the point \( (x, y) \) to the origin \( (0, 0) \).

To simplify \( \sqrt{x^2 + y^2} \), you can use the Pythagorean theorem, which states that in a right triangle with sides of lengths \( x \) and \( y \), and hypotenuse \( \sqrt{x^2 + y^2} \).

In polar coordinates, \( \sqrt{x^2 + y^2} \) simplifies directly to \( r \), where \( r \) is the radial coordinate or distance from the origin to the point \( (x, y) \).

In polar coordinates, the expression \( x^2 + y^2 \) represents the square of the radial distance \( r \) from the origin to the point \( (x, y) \), commonly denoted as \( r^2 \).

The transformation from Cartesian coordinates \( (x, y) \) to polar coordinates \( (r, \theta) \) is given by:

Here, \( r \) is the radial distance from the origin to the point, and \( \theta \) is the angle measured counterclockwise from the positive x-axis to the line segment connecting the origin to the point \( (x, y) \).

Polar coordinates provide a convenient way to describe points and perform calculations involving circular symmetry, such as in physics, engineering, and mathematics.

The expression \( x^2 + y^2 \) plays a crucial role in various advanced mathematical contexts:

• It appears in the equation of a circle: \( x^2 + y^2 = r^2 \), where \( r \) is the radius.
• It is fundamental in defining the Euclidean norm or magnitude of a vector \( (x, y) \) in Cartesian coordinates.
• In polar coordinates, \( x^2 + y^2 \) simplifies to \( r^2 \), representing the square of the radial distance \( r \) from the origin to \( (x, y) \).
• The expression is used extensively in quadratic forms, where matrices and vectors are manipulated to analyze systems in geometry, physics, and engineering.
• In trigonometry, \( x^2 + y^2 \) appears in formulas such as the Pythagorean identity and in deriving trigonometric identities related to circles and spheres.
• Its extension to higher dimensions involves forms like \( x^2 + y^2 + z^2 \), \( x^2 + y^2 + z^2 + w^2 \), which are crucial in multi-dimensional geometry and physics.

The expression \( x^2 + y^2 \) is fundamental in quadratic forms and finds extensive applications in various fields:

• **Geometry**: In geometry, quadratic forms like \( x^2 + y^2 \) define important curves such as circles, which are fundamental in understanding shapes and their properties.
• **Physics**: In physics, quadratic forms appear in the equations describing physical phenomena involving distances, energies, and potentials. For example, in mechanics, \( x^2 + y^2 \) represents the square of the distance from the origin, which is crucial in analyzing the dynamics of particles and systems.
• **Engineering**: In engineering, quadratic forms are used in structural analysis, optimization problems, and signal processing. They help in modeling physical systems and predicting their behavior under different conditions.
• **Computer Science**: In computer science, quadratic forms are utilized in algorithms related to optimization, numerical methods, and computer graphics. For instance, in computer graphics, \( x^2 + y^2 \) determines the radius of circles and spheres, essential for rendering and modeling objects.
• **Statistics**: In statistics, quadratic forms are used in multivariate analysis, where they play a role in covariance matrices and in defining measures of variability and dispersion.

In trigonometry, the expression \( x^2 + y^2 \) appears in several key contexts:

• It is central to the Pythagorean identity: \( \sin^2(\theta) + \cos^2(\theta) = 1 \), where \( \theta \) is an angle in a right triangle.
• It defines the radius squared \( r^2 \) in polar coordinates \( (r, \theta) \), relating the Cartesian coordinates \( (x, y) \) to trigonometric functions \( \sin \) and \( \cos \).
• It is used to derive trigonometric identities, such as the secant and cosecant functions through reciprocals and the tangent and cotangent functions through division of sine and cosine.
• It appears in formulas involving circles and spheres, where \( x^2 + y^2 \) represents the squared distance from the origin in the plane, essential for calculating geometric properties and distances.

In higher dimensions, the expression \( x^2 + y^2 \) extends to include more variables:

• In three dimensions, \( x^2 + y^2 + z^2 \) represents the squared distance from the origin to the point \( (x, y, z) \). This is crucial in defining spheres and in applications across physics, engineering, and computer graphics.
• In four dimensions, \( x^2 + y^2 + z^2 + w^2 \) serves a similar purpose, defining spheres and higher-dimensional analogues of circles. Such forms are used in theoretical physics and mathematics to explore concepts beyond traditional Euclidean spaces.
• Quadratic forms involving \( x^2 + y^2 \) generalize to higher dimensions through matrix representations, where they play a fundamental role in linear algebra, optimization, and understanding geometric transformations.
• Applications in computer science extend to computational geometry and data analysis, where higher-dimensional quadratic forms help model complex datasets and optimize algorithms.

Understanding the equation \( x^2 + y^2 \) through practical examples and problems helps solidify its concepts. Below are some detailed examples and problems to explore:

Example Problems in Algebra

• Problem 1: Find the Radius and Center of a Circle

  Given the equation \( x^2 + y^2 = 25 \), identify the center and radius of the circle.

  Solution: The given equation is in the standard form of a circle equation \( (x - h)^2 + (y - k)^2 = r^2 \). Here, \( h = 0 \), \( k = 0 \), and \( r^2 = 25 \). Thus, the center is at \( (0,0) \) and the radius is \( r = \sqrt{25} = 5 \).

• Problem 2: Intersection of a Line and a Circle

  Determine the points of intersection between the circle \( x^2 + y^2 = 16 \) and the line \( y = 2x \).

  Solution: Substitute \( y = 2x \) into the circle's equation:

  \( x^2 + (2x)^2 = 16 \)

  \( x^2 + 4x^2 = 16 \)

  \( 5x^2 = 16 \)

  \( x^2 = \frac{16}{5} \)

  \( x = \pm \sqrt{\frac{16}{5}} \)

  \( x = \pm \frac{4}{\sqrt{5}} = \pm \frac{4\sqrt{5}}{5} \)

  For \( y \): \( y = 2x \), so \( y = \pm \frac{8\sqrt{5}}{5} \). The points of intersection are \( \left( \frac{4\sqrt{5}}{5}, \frac{8\sqrt{5}}{5} \right) \) and \( \left( -\frac{4\sqrt{5}}{5}, -\frac{8\sqrt{5}}{5} \right) \).

Real-world Applications

• Application 1: Physics - Projectile Motion

  In projectile motion, the trajectory of an object can often be modeled using the equation \( x^2 + y^2 = r^2 \). For instance, to determine the maximum height and range of a projectile launched at a given speed and angle, one can use the parametric equations derived from this circular motion.

• Application 2: Engineering - Signal Processing

  In signal processing, especially in the analysis of circularly symmetric signals, the equation \( x^2 + y^2 \) is used to describe the power distribution within a circular region. This is crucial in designing antennas and other circularly symmetric systems.

These examples demonstrate the diverse applications and problems involving the equation \( x^2 + y^2 \), showcasing its significance in both theoretical and practical contexts.

Here are some practical example problems involving \(x^2 + y^2\) in algebra, demonstrating various techniques and applications.

Problem 1: Solving for \(x\) and \(y\) in a Circle Equation

Given the equation of a circle:

\(x^2 + y^2 = 25\)

Find the points where the circle intersects the line \(y = 3\).

1. Substitute \(y = 3\) into the circle equation: \[ x^2 + 3^2 = 25 \implies x^2 + 9 = 25 \]
2. Solve for \(x\): \[ x^2 = 25 - 9 \implies x^2 = 16 \implies x = \pm 4 \]
3. Therefore, the points of intersection are: \[ (4, 3) \text{ and } (-4, 3) \]

Problem 2: Distance Between Two Points

Find the distance between the points \((1, 2)\) and \((4, 6)\).

1. Use the distance formula: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
2. Substitute the coordinates: \[ d = \sqrt{(4 - 1)^2 + (6 - 2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
3. Therefore, the distance between the points is: \[ 5 \]

Problem 3: Simplifying an Expression

Simplify the expression \(\sqrt{x^2 + y^2}\) for \(x = 7\) and \(y = 24\).

1. Substitute \(x = 7\) and \(y = 24\): \[ \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} \]
2. Simplify the square root: \[ \sqrt{625} = 25 \]
3. Therefore, the simplified expression is: \[ 25 \]

Problem 4: Completing the Square

Complete the square for the expression \(x^2 + 6x + y^2\).

1. Focus on the \(x\) terms: \(x^2 + 6x\).
   • Take half of 6 and square it: \((6/2)^2 = 3^2 = 9\).
   • Add and subtract this value inside the expression: \[ x^2 + 6x + 9 - 9 + y^2 = (x + 3)^2 - 9 + y^2 \]
2. Therefore, the completed square form is: \[ (x + 3)^2 + y^2 - 9 \]

These problems illustrate how \(x^2 + y^2\) can be used in various algebraic contexts, such as finding intersections, distances, and simplifying expressions.

The equation \(x^2 + y^2\) has numerous practical applications in various fields. Here are some examples:

1. Navigation and GPS

In navigation systems, the distance between two points on a plane can be calculated using the distance formula derived from \(x^2 + y^2\). This is crucial for determining the shortest path or distance between two locations on a map.

1. Given two points \((x_1, y_1)\) and \((x_2, y_2)\), the distance \(d\) is: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]

2. Engineering and Construction

In engineering, especially in designing structures and buildings, the equation \(x^2 + y^2\) is used to calculate stress and strain, as well as to design circular components like arches and domes.

1. For instance, determining the optimal placement of support beams requires calculating distances and angles using this formula.

3. Physics: Circular Motion

In physics, objects in circular motion follow paths described by \(x^2 + y^2 = r^2\), where \(r\) is the radius of the circle. This is fundamental in studying the dynamics of particles in circular orbits.

1. The centripetal force \(F\) acting on a particle of mass \(m\) moving at a velocity \(v\) in a circle of radius \(r\) is: \[ F = \frac{mv^2}{r} \]

4. Computer Graphics

In computer graphics, the rendering of circles and ellipses on screens uses the equation \(x^2 + y^2\) to plot points accurately. This is essential for drawing shapes and animations.

1. Algorithms for anti-aliasing and smooth rendering rely on these calculations to improve visual quality.

5. Robotics and Autonomous Systems

Robotics utilizes \(x^2 + y^2\) in path planning and obstacle avoidance. Robots calculate distances to navigate efficiently within environments.

1. For example, a robot determining the best route to avoid obstacles will use distance formulas to find clear paths.

These examples illustrate the versatility of \(x^2 + y^2\) in solving practical problems across various disciplines.

In conclusion, the expression \( x^2 + y^2 \) plays a significant role in various fields of mathematics and real-world applications. It serves as the foundation for understanding geometric shapes such as circles and spheres, and it is crucial in solving problems involving distances in both two-dimensional and three-dimensional spaces.

We have explored its geometric interpretations, applications in geometry, simplification techniques, and advanced mathematical contexts. The formula not only helps in visualizing and calculating distances but also simplifies complex equations when transformed into polar coordinates or extended into higher dimensions.

Through practical examples and real-world applications, we have seen how \( x^2 + y^2 \) is utilized in fields such as engineering, physics, computer graphics, and navigation. Whether calculating the shortest path, determining the radius of a circle, or analyzing quadratic forms, this mathematical expression proves to be an essential tool.

As we continue to study and apply \( x^2 + y^2 \), we uncover more of its potential and versatility, making it a cornerstone in both theoretical and applied mathematics. By mastering this concept, students and professionals alike can enhance their problem-solving skills and contribute to advancements in technology and science.