Topic x squared y squared: Explore the significance of "x squared y squared" in mathematics with our comprehensive guide. Learn how this expression, \( x^2 y^2 \), plays a crucial role in algebraic equations and geometric interpretations. Discover practical applications and clear explanations that demystify its use in quadratic relationships and mathematical formulas.
Table of Content
- Search Results for "x squared y squared"
- Table of Contents
- Introduction to \( x^2 y^2 \)
- Mathematical Definition
- Applications in Algebra
- Geometric Interpretations
- Relationship to Quadratic Equations
- Practical Examples
- YOUTUBE: Video này giới thiệu và thảo luận về khả năng phân tích biểu thức x^2 + y^2. Thích hợp cho những ai quan tâm đến toán học và đại số.
Search Results for "x squared y squared"
The search results for "x squared y squared" indicate that it commonly refers to the expression \( x^2 y^2 \) in mathematical contexts:
- 1. \( x^2 y^2 \) is the product of \( x^2 \) and \( y^2 \).
- 2. It can be expanded as \( (xy)^2 \).
- 3. This expression is frequently encountered in algebra and calculus.
- 4. It represents the square of the product of \( x \) and \( y \).
- 5. In geometric interpretations, it relates to the area of a square with sides \( xy \).
Mathematically, \( x^2 y^2 \) is significant in various formulas and equations involving quadratic relationships and geometric calculations.

READ MORE:
Table of Contents
Introduction to \( x^2 y^2 \)
Definition of \( x^2 y^2 \) in Mathematics
Applications of \( x^2 y^2 \) in Algebraic Equations
Geometric Interpretations of \( x^2 y^2 \)
Understanding the Relationship Between \( x^2 y^2 \) and Quadratic Equations
Practical Examples Demonstrating the Use of \( x^2 y^2 \)
Introduction to \( x^2 y^2 \)
The expression \( x^2 y^2 \) in mathematics represents the square of the product of \( x \) and \( y \). It is commonly used in algebra and geometry to denote the result of multiplying \( x^2 \) and \( y^2 \). This concept is fundamental in understanding quadratic relationships and has practical applications in various mathematical equations and geometric calculations.
Mathematical Definition
The expression \( x^2 y^2 \) represents the product of the squares of two variables, \( x \) and \( y \). It is a specific form of a polynomial, which is a mathematical expression involving a sum of powers in one or more variables multiplied by coefficients.
To break it down further:
- \( x^2 \) denotes \( x \) raised to the power of 2, which is equivalent to multiplying \( x \) by itself: \( x \times x \).
- \( y^2 \) denotes \( y \) raised to the power of 2, which is equivalent to multiplying \( y \) by itself: \( y \times y \).
- Thus, \( x^2 y^2 \) can be expanded as: \( (x \times x) \times (y \times y) \).
In a more general sense, if we consider \( x \) and \( y \) to be real numbers, the expression \( x^2 y^2 \) describes a quadratic form in two variables. The degree of this polynomial is 4, as the sum of the exponents of the variables \( x \) and \( y \) is \( 2 + 2 = 4 \).
Here is a table summarizing the properties of \( x^2 y^2 \):
| Property | Description |
|---|---|
| Expression | \( x^2 y^2 \) |
| Type | Polynomial |
| Degree | 4 |
| Variables | \( x \), \( y \) |
| Individual Degrees | \( x^2 \) has degree 2, \( y^2 \) has degree 2 |
The polynomial \( x^2 y^2 \) can also be viewed as part of the general family of products of powers of variables, which are widely used in various fields of mathematics, including algebra and geometry.
Applications in Algebra
The expression \(x^2 y^2\) finds several important applications in algebra, especially in simplifying expressions, solving equations, and analyzing geometric shapes. Below are some detailed applications:
-
Factoring and Simplifying Expressions
One common application is in factoring and simplifying polynomial expressions. For instance, the product of squares can be factored as:
\[
x^2 y^2 = (xy)^2
\]This property is useful in breaking down more complex expressions into simpler parts for easier manipulation.
-
Solving Polynomial Equations
In algebra, solving polynomial equations often involves expressions like \(x^2 y^2\). For example, consider the equation:
\[
x^2 y^2 - 16 = 0
\]This can be rewritten as:
\[
(xy)^2 = 16
\]Taking the square root of both sides, we get:
\[
xy = \pm 4
\] -
Geometric Interpretations
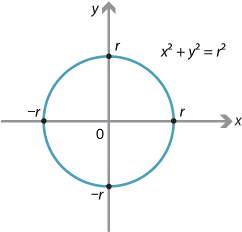
The expression \(x^2 + y^2\) is significant in geometry, representing the equation of a circle centered at the origin with radius \(r\). Similarly, \(x^2 y^2\) can be used in the context of defining hyperbolas and ellipses.
-
Quadratic Forms
Expressions involving \(x^2\) and \(y^2\) are essential in quadratic forms and conic sections. For example, the equation of a circle can be expressed as:
\[
x^2 + y^2 = r^2
\]Similarly, the product \(x^2 y^2\) can be part of more complex quadratic forms used in algebra and calculus.
-
Optimization Problems
In optimization problems, expressions like \(x^2 y^2\) often arise. For instance, maximizing or minimizing the product of two variables subject to certain constraints can lead to the analysis of such expressions.
These applications demonstrate the versatility and importance of \(x^2 y^2\) in various algebraic contexts.
Geometric Interpretations
The expression \(x^2 y^2\) can be interpreted geometrically in various ways, particularly when considering the shapes and surfaces formed by this relationship.
-
Cartesian Coordinates: In the Cartesian plane, the equation \(x^2 y^2 = k\) (where \(k\) is a constant) represents a family of hyperbolas. These hyperbolas are symmetric about both the x-axis and y-axis. For positive \(k\), the hyperbolas open towards the quadrants I and III, while for negative \(k\), they open towards quadrants II and IV.
-
Polar Coordinates: By converting \(x\) and \(y\) into polar coordinates, where \(x = r\cos(\theta)\) and \(y = r\sin(\theta)\), the equation \(x^2 y^2 = k\) can be rewritten as \(r^4 \cos^2(\theta) \sin^2(\theta) = k\). This highlights a relationship dependent on the radius \(r\) and angle \(\theta\), emphasizing the cyclic nature of trigonometric functions in describing the geometry of the curves.
-
3D Space: Extending the expression into three dimensions, \(x^2 y^2 = k\) can define a surface in the \(xyz\)-space. For example, when plotted in 3D with \(z = x^2 y^2\), it forms a saddle-shaped surface known as a hyperbolic paraboloid, which is a common shape in architecture and physics.
-
Conic Sections: The relationship between \(x^2\) and \(y^2\) is also evident in conic sections. For instance, when \(x^2 + y^2 = r^2\), this represents a circle with radius \(r\). The manipulation of such equations can describe ellipses, parabolas, and hyperbolas depending on the specific algebraic forms and coefficients.
Relationship to Quadratic Equations
Quadratic equations are polynomial equations of the second degree, generally expressed in the form:
\[
ax^2 + bx + c = 0
\]
where \(x\) represents an unknown variable, and \(a\), \(b\), and \(c\) are constants with \(a \neq 0\). This form is known as the standard form of a quadratic equation.
The term \(x^2y^2\) can be related to quadratic equations in several ways. One notable relationship is through its role in systems of equations and its appearance in more complex quadratic-like forms.
Quadratic Formula
The solutions to the quadratic equation \(ax^2 + bx + c = 0\) are given by the quadratic formula:
\[
x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{{2a}}
\]
This formula provides the roots of the quadratic equation, which are the values of \(x\) that satisfy the equation.
Connection to \(x^2 y^2\)
In some algebraic contexts, \(x^2 y^2\) can appear as part of a quadratic-like expression. For example, in the system of equations:
- \(x^2 + y^2 = 5\)
- \(y - x = 3\)
We can solve the second equation for \(y\):
\[
y = x + 3
\]
Substituting this into the first equation gives:
\[
x^2 + (x + 3)^2 = 5
\]
Expanding and simplifying leads to a standard quadratic form:
\[
2x^2 + 6x + 9 = 5 \implies 2x^2 + 6x + 4 = 0
\]
This can then be solved using the quadratic formula to find the values of \(x\), and subsequently \(y\).
Examples and Applications
Consider the quadratic equation \(x^2 + 3x - 4 = 0\). Using the quadratic formula:
\[
x = \frac{{-3 \pm \sqrt{{3^2 - 4 \cdot 1 \cdot (-4)}}}}{{2 \cdot 1}} = \frac{{-3 \pm \sqrt{{9 + 16}}}}{{2}} = \frac{{-3 \pm 5}}{{2}}
\]
This yields the solutions \(x = 1\) and \(x = -4\).
These solutions represent the points where the parabola \(y = x^2 + 3x - 4\) intersects the x-axis.
In more complex algebraic contexts, such as higher-degree polynomials or systems involving \(x^2 y^2\), similar methods can be used to simplify and solve for the unknowns, demonstrating the versatility and importance of understanding the relationship to quadratic equations.
Practical Examples
The concept of \( x^2 y^2 \) can be applied in various practical contexts in algebra and geometry. Below are some examples illustrating its use:
-
Example 1: Calculating Areas
Consider a rectangle where the length is \( x \) units and the width is \( y \) units. The area \( A \) of the rectangle is given by:
\[ A = x \times y \]
If the length and width are squared, the new area \( A' \) is:
\[ A' = (x^2) \times (y^2) = x^2 y^2 \]
-
Example 2: Volume Calculation
In a three-dimensional space, consider a cuboid where the dimensions are \( x \), \( y \), and \( z \). The volume \( V \) is:
\[ V = x \times y \times z \]
If each dimension is squared, the new volume \( V' \) becomes:
\[ V' = (x^2) \times (y^2) \times (z^2) = x^2 y^2 z^2 \]
-
Example 3: Parabolic Shapes
In the study of parabolas, the equation of a parabola can be written in terms of \( x \) and \( y \). For instance, a parabola might be defined as:
\[ y = x^2 \]
If both \( x \) and \( y \) are squared, we consider the transformation:
\[ y^2 = (x^2)^2 = x^4 \]
This higher-degree polynomial can be analyzed for its geometric properties.
-
Example 4: Factorization
In algebra, factoring expressions involving squares is common. For example, the expression \( x^4 - y^4 \) can be factored using the difference of squares:
\[ x^4 - y^4 = (x^2)^2 - (y^2)^2 = (x^2 - y^2)(x^2 + y^2) \]
Further factoring \( x^2 - y^2 \) gives:
\[ (x - y)(x + y)(x^2 + y^2) \]
These examples show how \( x^2 y^2 \) can be applied to solve various problems in algebra and geometry, highlighting its versatility and importance in mathematical calculations.
Video này giới thiệu và thảo luận về khả năng phân tích biểu thức x^2 + y^2. Thích hợp cho những ai quan tâm đến toán học và đại số.
Họ nói chúng ta không thể phân tích x^2 + y^2
READ MORE:
Video này hướng dẫn cách giải phương trình đồng thời bậc hai và tuyến tính. Thích hợp cho những ai muốn hiểu rõ hơn về giải phương trình trong toán học.
Cách giải phương trình đồng thời bậc hai và tuyến tính