Topic x squared function: The x squared function, written as \( f(x) = x^2 \), is a fundamental quadratic function in mathematics. It produces a parabolic graph, which is widely used in various fields such as physics, engineering, and economics. This article explores the properties, graphing techniques, and real-world applications of the x squared function.
Table of Content
- Understanding the X Squared Function
- Introduction to the X Squared Function
- Graphing the X Squared Function
- Standard Form of Quadratic Functions
- Vertex Form of Quadratic Functions
- Factored Form of Quadratic Functions
- Completing the Square Method
- Quadratic Formula
- Applications of the X Squared Function
- Graphical Representation and Interpretation
- Solving Quadratic Equations
- Properties of Parabolas
- Turning Points and Vertex Calculation
- Domain and Range of Quadratic Functions
- Symmetry and Axis of Quadratic Functions
- Examples and Practice Problems
- YOUTUBE:
Understanding the X Squared Function
The x squared function, often written as \( f(x) = x^2 \), is a fundamental quadratic function in mathematics. It produces a parabola that opens upwards, with its vertex at the origin (0,0). This function is frequently used to teach various algebraic concepts due to its simplicity and widespread applications.
Key Properties
- Standard Form: \( f(x) = ax^2 + bx + c \)
- Factored Form: \( f(x) = a(x - r_1)(x - r_2) \)
- Vertex Form: \( f(x) = a(x - h)^2 + k \)
The standard form is useful for identifying the y-intercept (\( c \)), while the factored form highlights the roots of the function, and the vertex form shows the vertex (h, k) directly.
Graphical Representation
The graph of \( f(x) = x^2 \) is a parabola that is symmetric about the y-axis:
- If \( a > 0 \), the parabola opens upwards.
- If \( a < 0 \), the parabola opens downwards.
The vertex of the parabola is the minimum point if \( a > 0 \) or the maximum point if \( a < 0 \).
Completing the Square
To convert the standard form to the vertex form, we use the method of completing the square:
Starting from \( f(x) = ax^2 + bx + c \), we can rewrite it as:
Thus, the vertex (h, k) of the parabola is:
Examples
-
Example 1: Solve by completing the square.
Given \( x^2 - 10x + 16 = 0 \), we add and subtract 25:
\( x^2 - 10x + 25 - 25 + 16 = 0 \)
Rewriting, we get:
\( (x - 5)^2 - 9 = 0 \)
So, \( (x - 5)^2 = 9 \) leading to \( x - 5 = \pm3 \), thus \( x = 8 \) or \( x = 2 \).
-
Example 2: Factorize the expression \( x^4 - 16 \).
Using the difference of squares:
\( x^4 - 16 = (x^2 + 4)(x^2 - 4) = (x^2 + 4)(x + 2)(x - 2) \).
Graphing calculators like are excellent tools to visualize and understand the behavior of the x squared function.
Applications
The x squared function is used in various real-world applications, from calculating areas to modeling physical phenomena. Its properties make it essential in fields such as physics, engineering, and economics.
| Function | Graph |
| Standard Form | \( f(x) = ax^2 + bx + c \) |
| Factored Form | \( f(x) = a(x - r_1)(x - r_2) \) |
| Vertex Form | \( f(x) = a(x - h)^2 + k \) |

READ MORE:
Introduction to the X Squared Function
The x squared function, denoted as \( f(x) = x^2 \), is a fundamental concept in mathematics. It represents a quadratic function where the variable \( x \) is raised to the power of 2, resulting in a parabolic graph that opens upwards. This function is widely used in various mathematical applications, including solving quadratic equations, analyzing parabolas, and modeling real-world scenarios.
- Definition: The x squared function is defined as \( f(x) = x^2 \).
- Graph: The graph of \( f(x) = x^2 \) is a parabola that opens upwards, with its vertex at the origin (0,0).
- Vertex: The vertex of the parabola represents the minimum point of the function when \( x \) is a real number.
- Symmetry: The parabola is symmetric about the y-axis, meaning it is a mirror image on either side of this axis.
- Applications: This function is crucial in solving quadratic equations, which can be factored, completed square, or using the quadratic formula.
- Completing the Square: This method involves rewriting the function in the form \( (x-h)^2 + k \), where \( (h, k) \) is the vertex of the parabola.
- Quadratic Formula: For a general quadratic equation \( ax^2 + bx + c = 0 \), the solutions can be found using \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \).
Understanding the x squared function is essential for mastering algebra and calculus. It not only helps in solving equations but also in understanding the properties of parabolas and their applications in various fields.
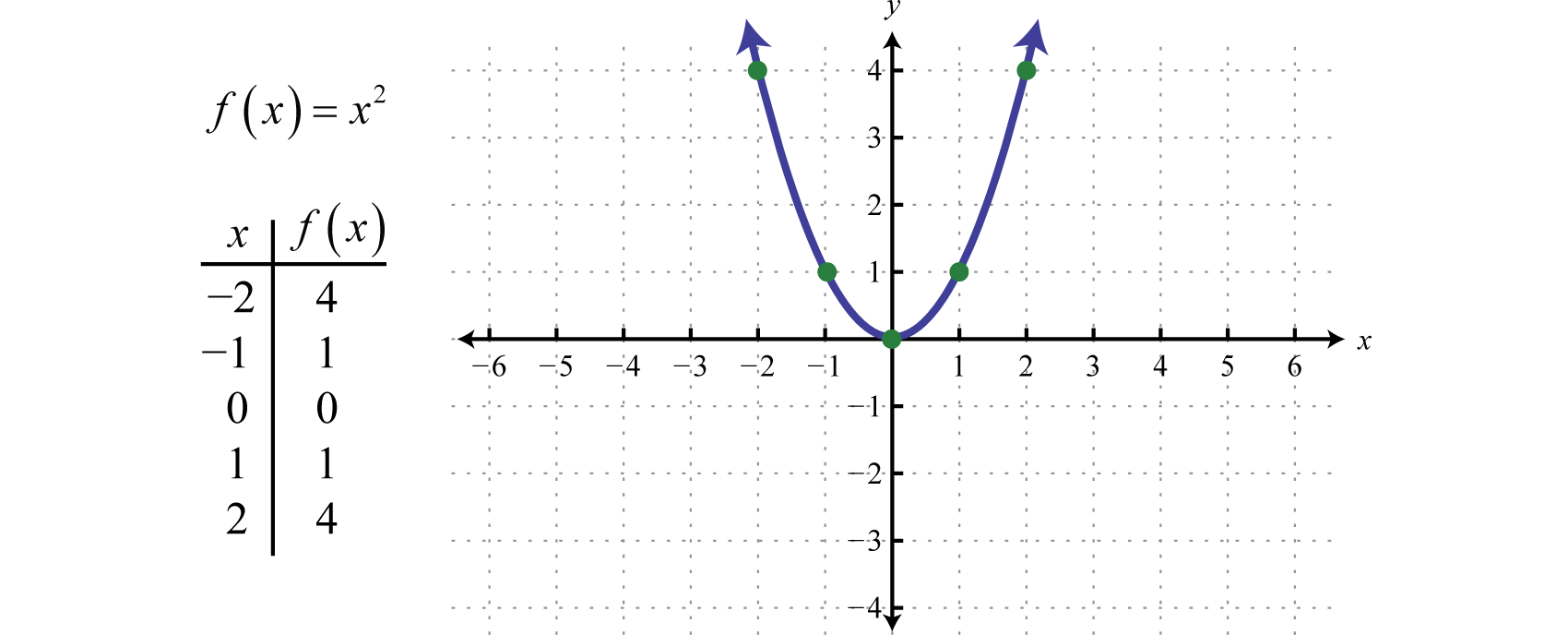
Graphing the X Squared Function
The x squared function, denoted as \(f(x) = x^2\), is a fundamental concept in mathematics. Its graph, a parabola, is symmetric about the y-axis and represents a key example of a quadratic function. Below is a detailed, step-by-step guide to graphing this function:
- Identify the Function: The function to graph is \(f(x) = x^2\).
- Plot the Vertex: The vertex of the parabola \(y = x^2\) is at the origin (0,0).
- Determine the Axis of Symmetry: The parabola is symmetric about the y-axis, which is \(x = 0\).
- Calculate Key Points: Select a few values of \(x\) to calculate corresponding \(y\) values:
- When \(x = -2\), \(y = (-2)^2 = 4\)
- When \(x = -1\), \(y = (-1)^2 = 1\)
- When \(x = 0\), \(y = 0^2 = 0\)
- When \(x = 1\), \(y = 1^2 = 1\)
- When \(x = 2\), \(y = 2^2 = 4\)
- Plot the Points: Plot the points \((-2, 4)\), \((-1, 1)\), \((0, 0)\), \((1, 1)\), and \((2, 4)\) on the coordinate plane.
- Draw the Parabola: Connect the points with a smooth, curved line to form the parabola.
The graph of \(f(x) = x^2\) showcases important characteristics:
- Shape: The graph is a U-shaped parabola opening upwards.
- Vertex: The lowest point is the vertex at (0,0).
- Symmetry: The graph is symmetric about the y-axis.
- Domain: The domain of \(f(x) = x^2\) is all real numbers, \(\mathbb{R}\).
- Range: The range is all non-negative real numbers, \([0, \infty)\).
By understanding these steps and characteristics, one can effectively graph the \(x^2\) function, a fundamental skill in algebra and calculus.
Standard Form of Quadratic Functions
The standard form of a quadratic function is one of the most commonly used forms in algebra. It is expressed as:
\[ f(x) = ax^2 + bx + c \]
where:
- a is the coefficient of \(x^2\) and determines the direction and width of the parabola.
- b is the coefficient of x and influences the position of the vertex and the axis of symmetry.
- c is the constant term and represents the y-intercept of the function, the point where the graph intersects the y-axis.
Here are the steps to understand the key features and graph the standard form of a quadratic function:
- Determine the direction of the parabola: If \(a > 0\), the parabola opens upwards. If \(a < 0\), the parabola opens downwards.
- Find the vertex: The vertex of the parabola can be found using the formula \(\left( -\frac{b}{2a}, f\left( -\frac{b}{2a} \right) \right)\). This point represents the maximum or minimum value of the function.
- Calculate the axis of symmetry: The vertical line that passes through the vertex is called the axis of symmetry and is given by \(x = -\frac{b}{2a}\).
- Identify the y-intercept: The y-intercept occurs at \(c\), the constant term of the quadratic equation, which is the point \((0, c)\).
- Find the x-intercepts: The x-intercepts (or roots) of the function can be found by solving the equation \(ax^2 + bx + c = 0\) using the quadratic formula \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \].
By following these steps, you can effectively graph and analyze the properties of a quadratic function in its standard form.
Vertex Form of Quadratic Functions
The vertex form of a quadratic function provides an insightful way to understand the properties and transformations of parabolas. The vertex form of a quadratic function is given by:
\[ y = a(x - h)^2 + k \]
Here, \( (h, k) \) is the vertex of the parabola, and the parameter \( a \) determines the width and direction of the parabola. If \( a \) is positive, the parabola opens upwards; if \( a \) is negative, the parabola opens downwards.
- Vertex Identification: The vertex \( (h, k) \) can be directly read from the equation, making it easy to graph the function. For example, in the equation \( y = 2(x + 3)^2 - 5 \), the vertex is \( (-3, -5) \).
- Transformations: The value of \( h \) translates the parabola horizontally, while \( k \) translates it vertically. This form highlights these transformations clearly.
- Graphing: To graph a quadratic function in vertex form, start by plotting the vertex. Then, use the value of \( a \) to determine the shape and direction of the parabola.
For example, consider the quadratic function \( y = (x - 2)^2 + 3 \):
- The vertex is \( (2, 3) \).
- The parabola opens upwards since \( a = 1 \) (positive).
- It is a standard parabola translated 2 units to the right and 3 units up.
Converting from standard form \( y = ax^2 + bx + c \) to vertex form involves completing the square. This process rearranges the equation to highlight the vertex, allowing for easier graphing and analysis.
| Standard Form | Vertex Form |
| \( y = x^2 + 6x + 8 \) | \( y = (x + 3)^2 - 1 \) |
To convert \( y = x^2 + 6x + 8 \) to vertex form:
- Rewrite \( y = x^2 + 6x + 8 \) by completing the square:
- Take half of the coefficient of \( x \) (which is 6), square it to get 9, and add and subtract this value inside the equation.
- Thus, \( y = (x^2 + 6x + 9) - 9 + 8 \).
- Factor the perfect square trinomial to get \( y = (x + 3)^2 - 1 \).
This vertex form, \( y = (x + 3)^2 - 1 \), shows the vertex at \( (-3, -1) \).
Factored Form of Quadratic Functions
The factored form of a quadratic function is one of the most useful representations, especially when solving for the roots of the equation. A quadratic function in factored form is expressed as:
\( ax^2 + bx + c = a(x - r_1)(x - r_2) \)
where \( r_1 \) and \( r_2 \) are the roots of the quadratic equation. Let's explore the process of factoring a quadratic function step by step:
-
Identify \( a \), \( b \), and \( c \): Start with the quadratic equation \( ax^2 + bx + c \). For example, consider the equation \( 2x^2 + 7x + 3 \).
-
Multiply \( a \) and \( c \): Calculate the product of the coefficients \( a \) and \( c \). For our example, \( 2 \times 3 = 6 \).
-
Find factors of the product that sum to \( b \): Determine two numbers that multiply to the product of \( a \) and \( c \) and add up to \( b \). Here, the numbers are 6 and 1 since \( 6 \times 1 = 6 \) and \( 6 + 1 = 7 \).
-
Rewrite the middle term: Rewrite the middle term \( bx \) using the two factors. Thus, \( 2x^2 + 7x + 3 \) becomes \( 2x^2 + 6x + x + 3 \).
-
Factor by grouping: Group the terms into two pairs and factor each pair. This gives \( 2x(x + 3) + 1(x + 3) \).
-
Extract the common factor: Factor out the common binomial factor. Therefore, \( 2x(x + 3) + 1(x + 3) \) becomes \( (2x + 1)(x + 3) \).
The factored form \( (2x + 1)(x + 3) \) reveals the roots of the quadratic function, which can be found by setting each factor to zero. For example:
- \( 2x + 1 = 0 \) gives \( x = -\frac{1}{2} \)
- \( x + 3 = 0 \) gives \( x = -3 \)
Thus, the solutions to the equation \( 2x^2 + 7x + 3 = 0 \) are \( x = -\frac{1}{2} \) and \( x = -3 \).
Completing the Square Method
The Completing the Square method is a technique used to solve quadratic equations by converting them into a perfect square trinomial. This process involves a few systematic steps that simplify the equation, making it easier to solve for the variable. Here’s a detailed step-by-step guide:
- Standard Form: Start with the quadratic equation in the form \( ax^2 + bx + c = 0 \). If \( a \neq 1 \), divide the entire equation by \( a \) to make the coefficient of \( x^2 \) equal to 1.
- Move Constant: Move the constant term to the right side of the equation: \( x^2 + \frac{b}{a}x = -\frac{c}{a} \).
- Completing the Square: Take the coefficient of \( x \) (which is \( \frac{b}{a} \)), divide it by 2, and square it. Add this value to both sides of the equation.
- Form a Perfect Square: The left side of the equation now forms a perfect square trinomial. Rewrite it as a square of a binomial: \( (x + \frac{b}{2a})^2 = \text{right side} \).
- Solve for \( x \): Take the square root of both sides and solve for \( x \).
Let's look at an example to illustrate these steps:
| Example: | Solve \( x^2 + 6x + 5 = 0 \) using Completing the Square. |
| Step 1: | Move the constant term: \( x^2 + 6x = -5 \). |
| Step 2: | Take half of the coefficient of \( x \) (which is 6), divide by 2 to get 3, then square it to get 9. Add 9 to both sides: \( x^2 + 6x + 9 = 4 \). |
| Step 3: | Rewrite the left side as a binomial square: \( (x + 3)^2 = 4 \). |
| Step 4: | Take the square root of both sides: \( x + 3 = \pm 2 \). |
| Step 5: | Solve for \( x \): \( x = -3 \pm 2 \), thus \( x = -1 \) or \( x = -5 \). |
This method not only helps in solving quadratic equations but also in understanding the properties of parabolas, such as their vertices and axes of symmetry.
Quadratic Formula
The quadratic formula is a method for solving quadratic equations of the form \(ax^2 + bx + c = 0\). The quadratic formula is derived from the process of completing the square and is given by:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Here is a step-by-step guide on how to use the quadratic formula:
- Identify the coefficients \(a\), \(b\), and \(c\) in the quadratic equation \(ax^2 + bx + c = 0\).
- Calculate the discriminant \(\Delta = b^2 - 4ac\).
- Determine the number and type of solutions based on the discriminant:
- If \(\Delta > 0\), there are two distinct real solutions.
- If \(\Delta = 0\), there is exactly one real solution (a repeated root).
- If \(\Delta < 0\), there are two complex solutions.
- Use the quadratic formula to find the solutions:
- For two distinct real solutions: \[ x_1 = \frac{-b + \sqrt{b^2 - 4ac}}{2a}, \quad x_2 = \frac{-b - \sqrt{b^2 - 4ac}}{2a} \]
- For one real solution: \[ x = \frac{-b}{2a} \]
- For two complex solutions: \[ x_1 = \frac{-b + i\sqrt{4ac - b^2}}{2a}, \quad x_2 = \frac{-b - i\sqrt{4ac - b^2}}{2a} \]
Let's look at an example:
Suppose we have the quadratic equation \(2x^2 + 3x - 2 = 0\). Here, \(a = 2\), \(b = 3\), and \(c = -2\).
- Calculate the discriminant: \[ \Delta = b^2 - 4ac = 3^2 - 4 \cdot 2 \cdot (-2) = 9 + 16 = 25 \]
- Since \(\Delta > 0\), there are two distinct real solutions.
- Apply the quadratic formula: \[ x_1 = \frac{-3 + \sqrt{25}}{2 \cdot 2} = \frac{-3 + 5}{4} = \frac{2}{4} = 0.5 \] \[ x_2 = \frac{-3 - \sqrt{25}}{2 \cdot 2} = \frac{-3 - 5}{4} = \frac{-8}{4} = -2 \]
Therefore, the solutions to the equation \(2x^2 + 3x - 2 = 0\) are \(x = 0.5\) and \(x = -2\).
The quadratic formula is a powerful tool for solving any quadratic equation and helps in understanding the nature of the solutions based on the discriminant.
Applications of the X Squared Function
The x squared function, or quadratic function, is widely used in various real-world applications. Here are some notable examples:
1. Physics and Engineering
In physics, the quadratic function is essential for describing the motion of objects under constant acceleration, such as the trajectory of projectiles. The general equation used is:
where \( y \) represents the height of the object at time \( x \), \( a \) is the acceleration due to gravity, \( b \) is the initial velocity, and \( c \) is the initial height.
2. Economics and Business
Quadratic functions are used to model cost and revenue functions. For example, the total profit (\( P \)) of producing \( x \) items can be represented by a quadratic equation:
Here, the coefficients \( a \), \( b \), and \( c \) represent various fixed and variable costs and revenues.
3. Agriculture
Farmers use quadratic functions to determine the optimal area for planting crops to maximize yield. The area of a rectangular plot can be expressed as:
where \( L \) and \( W \) are lengths that can be represented as linear functions of \( x \), resulting in a quadratic function for the area.
4. Architecture
In architecture, parabolic arches are a common design element. The shape of these arches can be described by a quadratic function, ensuring both aesthetic appeal and structural stability.
5. Medicine
Quadratic functions are used in medicine to model the progression of diseases or the concentration of drugs in the bloodstream over time. For instance, the concentration (\( C \)) of a drug can be modeled by:
where \( t \) is time, and \( a \), \( b \), and \( c \) are constants determined by the drug's properties.
6. Sports
The parabolic trajectory of a ball in sports like basketball or soccer can be analyzed using quadratic functions. The path of the ball follows:
where \( y \) is the height of the ball and \( x \) is the horizontal distance.
Examples and Practice Problems
- Calculate the maximum height of a ball thrown with an initial velocity of 20 m/s from a height of 2 m.
- Determine the optimal price point to maximize profit for a product, given the revenue and cost functions.
- Model the area of a garden plot that maximizes yield using a quadratic function.

Graphical Representation and Interpretation
The x squared function, also known as the quadratic function, is represented by \( f(x) = x^2 \). This function is characterized by its parabolic graph which opens upwards, forming a U-shaped curve.
Key Features of the Parabola
- Vertex: The vertex is the highest or lowest point on the graph of a quadratic function. For the function \( f(x) = x^2 \), the vertex is at the origin (0,0).
- Axis of Symmetry: The parabola is symmetric about a vertical line that passes through the vertex. For \( f(x) = x^2 \), the axis of symmetry is the y-axis, or the line \( x = 0 \).
- Direction: Since the coefficient of \( x^2 \) is positive, the parabola opens upwards.
Steps to Graph the X Squared Function
- Start by plotting the vertex at the origin (0,0).
- Identify the axis of symmetry, which in this case is the y-axis.
- Choose a few values for x, both positive and negative, and calculate the corresponding y values to plot points. For example:
- When \( x = 1 \), \( f(1) = 1^2 = 1 \) (point: (1,1))
- When \( x = -1 \), \( f(-1) = (-1)^2 = 1 \) (point: (-1,1))
- When \( x = 2 \), \( f(2) = 2^2 = 4 \) (point: (2,4))
- When \( x = -2 \), \( f(-2) = (-2)^2 = 4 \) (point: (-2,4))
- Plot these points on a graph.
- Draw a smooth curve through the points, ensuring the curve is symmetrical about the y-axis.
Interpretation of the Graph
The graph of the quadratic function \( f(x) = x^2 \) shows several important properties:
- Minimum Point: The vertex (0,0) represents the minimum point of the function.
- Increasing/Decreasing Intervals: The function decreases on the interval \( (-\infty, 0) \) and increases on the interval \( (0, \infty) \).
- Intercepts: The graph intersects the y-axis at (0,0) and does not intersect the x-axis at any other point.
Example
Consider the quadratic function \( f(x) = (x - 2)^2 - 3 \). To graph this function:
- Identify the vertex: The vertex form \( (x - h)^2 + k \) reveals the vertex is at (2, -3).
- Plot the vertex at (2, -3).
- Determine the axis of symmetry, which is the line \( x = 2 \).
- Choose values for x and calculate corresponding y values to plot points, ensuring symmetry about \( x = 2 \).
- Draw a smooth curve through the points.
This detailed approach helps visualize and interpret the behavior of quadratic functions through their graphical representations.
Solving Quadratic Equations
Quadratic equations are equations of the form \(ax^2 + bx + c = 0\), where \(a\), \(b\), and \(c\) are constants. Solving quadratic equations can be done using several methods:
1. Factoring
Factoring involves writing the quadratic equation as a product of two binomials. For example, to solve \(x^2 + 2x - 15 = 0\), we factor it as \((x + 5)(x - 3) = 0\). This gives us the solutions:
- \(x + 5 = 0 \Rightarrow x = -5\)
- \(x - 3 = 0 \Rightarrow x = 3\)
Thus, the solutions are \(x = -5\) and \(x = 3\).
2. Completing the Square
Completing the square involves rewriting the quadratic equation in the form \((x - p)^2 = q\). For example, to solve \(x^2 + 6x + 5 = 0\), we rewrite it as:
- Move the constant term to the other side: \(x^2 + 6x = -5\).
- Add the square of half the coefficient of \(x\) to both sides: \(x^2 + 6x + 9 = 4\).
- Rewrite as a square: \((x + 3)^2 = 4\).
- Take the square root of both sides: \(x + 3 = \pm 2\).
- Solve for \(x\): \(x = -3 \pm 2\), giving \(x = -1\) or \(x = -5\).
3. Quadratic Formula
The quadratic formula is a universal method for solving any quadratic equation. The formula is:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
To use the formula, simply substitute the values of \(a\), \(b\), and \(c\) from your quadratic equation \(ax^2 + bx + c = 0\). For example, to solve \(2x^2 - 4x - 6 = 0\), we identify \(a = 2\), \(b = -4\), and \(c = -6\), and substitute them into the formula:
\[
x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4 \cdot 2 \cdot (-6)}}{2 \cdot 2} = \frac{4 \pm \sqrt{16 + 48}}{4} = \frac{4 \pm \sqrt{64}}{4} = \frac{4 \pm 8}{4}
\]
This gives two solutions:
- \(x = \frac{4 + 8}{4} = 3\)
- \(x = \frac{4 - 8}{4} = -1\)
4. Graphical Method
Quadratic equations can also be solved by graphing the function \(y = ax^2 + bx + c\) and finding the points where the graph intersects the x-axis. These points, called the roots or zeros, are the solutions to the equation.
For example, the graph of \(y = x^2 - 4\) intersects the x-axis at \(x = 2\) and \(x = -2\), so the solutions to \(x^2 - 4 = 0\) are \(x = 2\) and \(x = -2\).
By using these methods, you can solve any quadratic equation efficiently and accurately.
Properties of Parabolas
The parabola is a key graph in algebra, characterized by its U-shape. Here are the main properties and components of parabolas:
1. Standard Form and Vertex Form
The standard form of a quadratic equation is:
\[ y = ax^2 + bx + c \]
The vertex form of a quadratic equation is:
\[ y = a(x-h)^2 + k \]
Where \((h, k)\) is the vertex of the parabola.
2. Vertex
The vertex is the highest or lowest point on the parabola, depending on whether it opens upwards or downwards. For the equation \( y = ax^2 + bx + c \), the vertex \((h, k)\) can be found using:
\[ h = -\frac{b}{2a} \]
\[ k = f(h) \]
3. Axis of Symmetry
The axis of symmetry is a vertical line that passes through the vertex of the parabola. The equation for the axis of symmetry is:
\[ x = h \]
4. Direction of Opening
- If \( a > 0 \), the parabola opens upwards.
- If \( a < 0 \), the parabola opens downwards.
5. Focus and Directrix
The focus is a point inside the parabola used to define its shape. The directrix is a line outside the parabola used for the same purpose. For a parabola \( y = a(x-h)^2 + k \), the focus is located at:
\[ (h, k + \frac{1}{4a}) \]
The directrix is given by the equation:
\[ y = k - \frac{1}{4a} \]
6. Latus Rectum
The latus rectum is a line segment that passes through the focus and is perpendicular to the axis of symmetry. Its length is given by:
\[ \frac{4}{|a|} \]
7. Intercepts
- Y-Intercept: The point where the parabola crosses the y-axis. This occurs when \( x = 0 \).
- X-Intercepts: The points where the parabola crosses the x-axis. These are found by solving \( ax^2 + bx + c = 0 \).
8. Symmetry
The parabola is symmetric with respect to its axis of symmetry. This means that if a point \((x, y)\) lies on the parabola, then the point \((2h-x, y)\) also lies on the parabola.
Examples
- For \( y = x^2 \), the vertex is at \((0, 0)\), the focus is at \((0, \frac{1}{4})\), and the directrix is \( y = -\frac{1}{4} \).
- For \( y = -2(x-1)^2 + 3 \), the vertex is at \((1, 3)\), the focus is at \((1, 3 - \frac{1}{8})\), and the directrix is \( y = 3 + \frac{1}{8} \).
Understanding these properties allows us to graph and analyze parabolas effectively, providing insight into their behavior and applications in various mathematical contexts.
Turning Points and Vertex Calculation
The turning point of a quadratic function, also known as the vertex, is a critical feature of its graph. The vertex represents the maximum or minimum point on the parabola. For a quadratic function in the form:
\[ f(x) = ax^2 + bx + c \]
The vertex can be found using the formula:
\[ x = -\frac{b}{2a} \]
Once you have the x-coordinate of the vertex, you can substitute it back into the original function to find the y-coordinate.
- Find the x-coordinate of the vertex using the formula:
- Substitute the x-coordinate back into the quadratic function to find the y-coordinate:
\[ x_v = -\frac{b}{2a} \]
\[ y_v = f(x_v) = a(x_v)^2 + b(x_v) + c \]
Thus, the coordinates of the vertex are \((x_v, y_v)\).
Example Calculation
Consider the quadratic function:
\[ f(x) = 2x^2 - 4x + 1 \]
- Calculate the x-coordinate of the vertex:
- Substitute \( x_v = 1 \) back into the function to find the y-coordinate:
\[ x_v = -\frac{-4}{2 \cdot 2} = \frac{4}{4} = 1 \]
\[ y_v = 2(1)^2 - 4(1) + 1 = 2 - 4 + 1 = -1 \]
Therefore, the vertex of the function \( f(x) = 2x^2 - 4x + 1 \) is at \( (1, -1) \).
Graphical Representation
The vertex is the highest or lowest point on the graph of the quadratic function, depending on the sign of the coefficient \(a\):
- If \( a > 0 \), the parabola opens upwards, and the vertex is the minimum point.
- If \( a < 0 \), the parabola opens downwards, and the vertex is the maximum point.
Summary
The vertex form of a quadratic function can also be expressed as:
\[ f(x) = a(x - h)^2 + k \]
where \( (h, k) \) is the vertex of the parabola. This form can be useful for easily identifying the vertex and graphing the function.
Understanding the vertex of a quadratic function is essential for solving problems related to graphing, optimization, and real-world applications of quadratic equations.

Domain and Range of Quadratic Functions
The domain and range of a quadratic function are fundamental concepts that describe the input and output values of the function.
Domain
The domain of a quadratic function is the set of all possible input values (x-values). Since a quadratic function is defined for all real numbers, its domain is:
\[ \text{Domain}: \, (-\infty, \infty) \]
This means that you can substitute any real number for \( x \) in the quadratic function \( f(x) = ax^2 + bx + c \), and the function will produce a valid output.
Range
The range of a quadratic function is the set of all possible output values (y-values). The range depends on the direction in which the parabola opens, which is determined by the coefficient \( a \):
- If \( a > 0 \), the parabola opens upwards, and the range is:
- If \( a < 0 \), the parabola opens downwards, and the range is:
\[ \text{Range}: \, [k, \infty) \]
\[ \text{Range}: \, (-\infty, k] \]
Here, \( k \) represents the y-coordinate of the vertex, which is the minimum value when \( a > 0 \) and the maximum value when \( a < 0 \).
Example Calculation
Consider the quadratic function:
\[ f(x) = -3x^2 + 6x - 2 \]
- First, find the vertex of the function to determine \( k \):
- Substitute \( x_v = 1 \) back into the function to find the y-coordinate:
The x-coordinate of the vertex is given by:
\[ x_v = -\frac{b}{2a} = -\frac{6}{2 \cdot -3} = 1 \]
\[ y_v = f(1) = -3(1)^2 + 6(1) - 2 = -3 + 6 - 2 = 1 \]
Therefore, the vertex of the function \( f(x) = -3x^2 + 6x - 2 \) is at \( (1, 1) \).
Since \( a < 0 \), the parabola opens downwards, and the range is:
\[ \text{Range}: \, (-\infty, 1] \]
Summary
In summary, for any quadratic function \( f(x) = ax^2 + bx + c \):
- The domain is always all real numbers:
- The range depends on the direction of the parabola:
- For \( a > 0 \):
- For \( a < 0 \):
- Where \( k \) is the y-coordinate of the vertex, calculated by substituting the x-coordinate of the vertex back into the function.
\[ (-\infty, \infty) \]
\[ [k, \infty) \]
\[ (-\infty, k] \]
Understanding the domain and range of quadratic functions is crucial for analyzing and graphing these functions effectively.
Symmetry and Axis of Quadratic Functions
Quadratic functions exhibit a property of symmetry, which is reflected in their graphs. This symmetry is centered around a vertical line called the axis of symmetry. Understanding this concept is essential for graphing and analyzing quadratic functions.
Axis of Symmetry
The axis of symmetry of a quadratic function \( f(x) = ax^2 + bx + c \) is a vertical line that passes through the vertex of the parabola. The equation for the axis of symmetry can be found using the formula for the x-coordinate of the vertex:
\[ x = -\frac{b}{2a} \]
This line divides the parabola into two mirror-image halves, ensuring that the function's values on either side of the axis are symmetrical.
Example Calculation
Consider the quadratic function:
\[ f(x) = 3x^2 - 6x + 2 \]
- Calculate the x-coordinate of the vertex to find the axis of symmetry:
- Thus, the equation of the axis of symmetry is:
\[ x = -\frac{-6}{2 \cdot 3} = \frac{6}{6} = 1 \]
\[ x = 1 \]
Symmetry in the Graph
The graph of a quadratic function is symmetric with respect to its axis of symmetry. This means that if you pick any point on the parabola, there will be another point directly opposite it, at the same distance from the axis of symmetry but on the other side.
For instance, if \( (x_1, y_1) \) is a point on the parabola, then there exists another point \( (x_2, y_2) \) such that:
\[ x_2 = 2h - x_1 \]
where \( h \) is the x-coordinate of the vertex (axis of symmetry). The y-values will be the same, so \( y_2 = y_1 \).
Graphical Representation
To better understand symmetry, consider the following steps to graph a quadratic function:
- Find the vertex and plot it on the coordinate plane.
- Draw the axis of symmetry as a dashed vertical line through the vertex.
- Choose points on one side of the axis of symmetry, calculate their y-values, and plot them.
- Reflect these points across the axis of symmetry to find their symmetrical counterparts.
This process helps in accurately sketching the parabola by leveraging its symmetrical property.
Summary
The symmetry and axis of quadratic functions are crucial for understanding their graphical behavior. The key points to remember are:
- The axis of symmetry is a vertical line given by \( x = -\frac{b}{2a} \).
- The parabola is symmetric with respect to this axis.
- Reflecting points across the axis of symmetry helps in accurately plotting the quadratic function.
Mastering these concepts will aid in analyzing and graphing quadratic functions more effectively.
Examples and Practice Problems
Practicing problems involving the x squared function helps to reinforce the concepts and techniques used in working with quadratic functions. Below are several examples and practice problems, each with a detailed solution.
Example 1: Finding the Vertex
Consider the quadratic function:
\[ f(x) = 2x^2 - 4x + 1 \]
- Find the x-coordinate of the vertex:
- Substitute \( x_v = 1 \) back into the function to find the y-coordinate:
\[ x_v = -\frac{b}{2a} = -\frac{-4}{2 \cdot 2} = \frac{4}{4} = 1 \]
\[ y_v = f(1) = 2(1)^2 - 4(1) + 1 = 2 - 4 + 1 = -1 \]
Therefore, the vertex of the function \( f(x) = 2x^2 - 4x + 1 \) is at \( (1, -1) \).
Example 2: Graphing a Quadratic Function
Graph the quadratic function:
\[ f(x) = -x^2 + 2x + 3 \]
- Find the vertex:
- Find the y-intercept (when \( x = 0 \)):
- Find the x-intercepts by solving \( f(x) = 0 \):
\[ x_v = -\frac{b}{2a} = -\frac{2}{2 \cdot -1} = 1 \]
\[ y_v = f(1) = -1(1)^2 + 2(1) + 3 = -1 + 2 + 3 = 4 \]
Vertex: \( (1, 4) \)
\[ f(0) = -0^2 + 2(0) + 3 = 3 \]
Y-intercept: \( (0, 3) \)
\[ -x^2 + 2x + 3 = 0 \]
Using the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
\[ x = \frac{-2 \pm \sqrt{4 + 12}}{-2} = \frac{-2 \pm 4}{-2} \]
\[ x = -1 \quad \text{or} \quad x = 3 \]
X-intercepts: \( (-1, 0) \) and \( (3, 0) \)
Plot these points and draw the parabola.
Practice Problems
- Find the vertex and axis of symmetry for the function \( f(x) = 3x^2 + 6x - 2 \).
- Solve the quadratic equation \( x^2 - 4x - 5 = 0 \) and find the x-intercepts.
- Determine the domain and range of the function \( f(x) = -2x^2 + 8x - 3 \).
- Graph the quadratic function \( f(x) = \frac{1}{2}x^2 - 3x + 1 \) and identify the key features.
- Rewrite the quadratic function \( f(x) = x^2 + 4x + 4 \) in vertex form and identify the vertex.
Solutions to Practice Problems
- For \( f(x) = 3x^2 + 6x - 2 \):
\[ x_v = -\frac{6}{2 \cdot 3} = -1 \]
\[ y_v = f(-1) = 3(-1)^2 + 6(-1) - 2 = 3 - 6 - 2 = -5 \]Vertex: \( (-1, -5) \)
Axis of symmetry: \( x = -1 \)
- Solve \( x^2 - 4x - 5 = 0 \):
\[ x = \frac{4 \pm \sqrt{16 + 20}}{2} = \frac{4 \pm \sqrt{36}}{2} = \frac{4 \pm 6}{2} \]
\[ x = 5 \quad \text{or} \quad x = -1 \]X-intercepts: \( (5, 0) \) and \( (-1, 0) \)
- For \( f(x) = -2x^2 + 8x - 3 \):
Domain: \( (-\infty, \infty) \)
Vertex: \( x = \frac{-8}{2 \cdot -2} = 2 \)
\[ y = f(2) = -2(2)^2 + 8(2) - 3 = -8 + 16 - 3 = 5 \]Range: \( (-\infty, 5] \)
- Graph \( f(x) = \frac{1}{2}x^2 - 3x + 1 \):
Vertex: \( x = \frac{3}{1} = 3 \)
\[ y = f(3) = \frac{1}{2}(3)^2 - 3(3) + 1 = \frac{9}{2} - 9 + 1 = -\frac{7}{2} \]Vertex: \( (3, -\frac{7}{2}) \)
Y-intercept: \( (0, 1) \)
Find x-intercepts by solving \( \frac{1}{2}x^2 - 3x + 1 = 0 \):
\[ x = 1 \quad \text{or} \quad x = 2 \] - Rewrite \( f(x) = x^2 + 4x + 4 \) in vertex form:
Complete the square:
\[ f(x) = (x + 2)^2 \]Vertex: \( (-2, 0) \)
Đạo hàm trực quan của x bình phương
READ MORE:
Nhanh lên! Đồ thị y = x bình phương









:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)

