Topic 3x + x squared: Discover the fascinating world of quadratic expressions with our comprehensive guide on "3x + x squared". This article explores the basics of algebraic expressions, graphing techniques, and real-life applications, providing you with a solid foundation to master these essential mathematical concepts. Join us as we delve into the intricacies of polynomials and enhance your problem-solving skills.
Table of Content
Understanding the Expression: \(3x + x^2\)
The expression \(3x + x^2\) is a polynomial equation that combines a linear term and a quadratic term. Below are detailed explanations and various aspects related to this expression.
Expression Breakdown
The expression can be broken down as follows:
- \(3x\): This is a linear term where the variable \(x\) is raised to the power of 1.
- \(x^2\): This is a quadratic term where the variable \(x\) is squared.
Graphing the Expression
When graphed, the expression \(3x + x^2\) represents a parabola that opens upwards, with the vertex depending on the coefficients and constants involved.
Solving the Expression
To solve \(3x + x^2 = 0\), you can factorize or use the quadratic formula:
Factorization:
- Set the equation to zero: \(x^2 + 3x = 0\).
- Factor out \(x\): \(x(x + 3) = 0\).
- Find the roots: \(x = 0\) and \(x = -3\).
Quadratic Formula:
Using \(ax^2 + bx + c = 0\) where \(a = 1\), \(b = 3\), and \(c = 0\):
\[
x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a}
\]
Substitute the values to find the roots.
Applications
Such expressions are frequently used in algebra to describe various phenomena in physics, engineering, and economics.
Related Concepts
Tools and Resources
Here are some online tools to help you understand and solve polynomial expressions:

READ MORE:
Introduction
Algebra is a fundamental branch of mathematics that involves the study of mathematical symbols and the rules for manipulating these symbols. It is essential for solving equations and understanding the relationships between variables. One common type of algebraic expression is the polynomial, which can include terms like 3x and x2.
A polynomial is a mathematical expression consisting of variables, coefficients, and exponents, combined using addition, subtraction, and multiplication. For example, the expression 3x + x2 is a polynomial with two terms: one linear term 3x and one quadratic term x2.
Polynomials are categorized based on the number of terms they contain:
- Monomial: A polynomial with a single term, such as 5x or 7.
- Binomial: A polynomial with two terms, such as 3x + 4.
- Trinomial: A polynomial with three terms, such as x2 + 5x + 6.
Understanding the structure and properties of polynomials is crucial for solving algebraic equations. In the case of 3x + x2, we can explore how to simplify, factor, and graph these expressions, leading to a deeper comprehension of algebraic principles and their applications.
In this guide, we will delve into various aspects of polynomials, starting with basic definitions and moving on to more complex concepts like quadratic equations and graphing. We will also discuss practical applications and provide step-by-step solutions to common problems, ensuring a comprehensive understanding of the topic.
Understanding Algebraic Expressions
Algebraic expressions are mathematical phrases that can include numbers, variables, and operation symbols. They are foundational in algebra and are used to represent relationships and formulas. Unlike algebraic equations, expressions do not contain an equality sign.
Here are some key concepts to understand:
- Variables: Symbols such as \(x\), \(y\), or \(z\) that represent unknown values.
- Constants: Specific, fixed numbers within the expression (e.g., 5, -3).
- Coefficients: Numbers multiplied by the variables (e.g., in \(5x\), 5 is the coefficient).
- Terms: Individual parts of the expression separated by addition or subtraction (e.g., in \(3x + 4y - 7\), there are three terms: \(3x\), \(4y\), and -7).
Algebraic expressions can be categorized into different types based on the number of terms they have:
- Monomial: An expression with a single term (e.g., \(3x\)).
- Binomial: An expression with two unlike terms (e.g., \(5xy + 8\)).
- Polynomial: An expression with more than one term (e.g., \(x^2 + 2x + 3\)).
To simplify algebraic expressions, follow these steps:
- Remove Parentheses: Use the distributive property to eliminate parentheses. For example, \(a(b+c) = ab + ac\).
- Combine Like Terms: Add or subtract terms that have the same variable raised to the same power. For example, \(3x + 4x = 7x\).
- Simplify Coefficients: Reduce fractions and simplify any numerical coefficients.
- Arrange Terms: Order terms by descending powers of the variables for clarity, although this is not always necessary for simplification.
- Factor Out Common Factors: If all terms share a common factor, factor it out. For instance, \(4x^2 - 8x = 4x(x - 2)\).
Understanding and manipulating algebraic expressions is essential for solving equations and modeling real-world problems. Practice simplifying and working with these expressions to gain a deeper understanding of algebraic concepts.
Simplifying Expressions
Simplifying algebraic expressions involves reducing them to their simplest form without changing their values. This process typically involves combining like terms, removing unnecessary constants, and rearranging the expression for easier manipulation. Let's break down the steps to simplify an expression:
-
Combine Like Terms:
Look for terms with the same variables and exponents and combine them using appropriate operations. For example, to simplify \(3x + x^2 + 2x\), combine the \(3x\) and \(2x\) to get \(5x\). The expression becomes \(5x + x^2\).
-
Remove Unnecessary Terms:
Terms with a coefficient of zero can be removed. For example, \(3x + 0y\) simplifies to \(3x\).
-
Factor the Expression:
Identify common factors and factor them out using parentheses. For instance, \(4x + 6x\) can be factored as \(2x(2 + 3) = 10x\).
-
Use Properties of Exponents:
When dealing with exponents, use these properties:
- \(a^m \cdot a^n = a^{m+n}\)
- \(a^m / a^n = a^{m-n}\)
- \((a^m)^n = a^{m \cdot n}\)
For example, \(x^2 \cdot x^3 = x^{2+3} = x^5\).
-
Use Properties of Logarithms (if applicable):
Apply logarithmic properties to simplify expressions involving logarithms:
- \(\log(a^m) = m \cdot \log(a)\)
- \(\log(a \cdot b) = \log(a) + \log(b)\)
By following these steps, you can simplify most algebraic expressions effectively, making them easier to work with and understand. Remember, the goal is to rewrite the expression in a more convenient form while maintaining its original value.
Quadratic Equations
Quadratic equations are polynomial equations of the second degree, typically written in the form:
\[ ax^2 + bx + c = 0 \]
where \(a\), \(b\), and \(c\) are constants, and \(x\) represents an unknown variable. The value of \(a\) cannot be zero, as this would make the equation linear rather than quadratic.
Methods to Solve Quadratic Equations
There are several methods to solve quadratic equations, including:
- Factoring: This involves expressing the quadratic equation as a product of two binomials. For example, \(x^2 + 5x + 6\) can be factored as \((x + 2)(x + 3)\).
- Using the Quadratic Formula: The quadratic formula is given by: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] This formula provides the solutions to any quadratic equation.
- Completing the Square: This method involves rearranging the equation to form a perfect square trinomial, making it easier to solve for \(x\).
- Graphing: By graphing the quadratic equation, the points where the graph intersects the x-axis represent the solutions to the equation.
Using the Quadratic Formula
The quadratic formula is a universal method for solving quadratic equations. To use the quadratic formula, follow these steps:
- Identify the coefficients \(a\), \(b\), and \(c\) in the quadratic equation \(ax^2 + bx + c = 0\).
- Substitute these values into the formula: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
- Calculate the discriminant, \(b^2 - 4ac\):
- If the discriminant is positive, the equation has two real solutions.
- If the discriminant is zero, the equation has one real solution.
- If the discriminant is negative, the equation has two complex solutions.
- Solve for \(x\) by performing the arithmetic operations indicated by the formula.
Example: Solving a Quadratic Equation
Consider the quadratic equation \(5x^2 + 6x + 1 = 0\). To solve using the quadratic formula:
- Identify the coefficients: \(a = 5\), \(b = 6\), and \(c = 1\).
- Substitute these values into the formula: \[ x = \frac{-6 \pm \sqrt{6^2 - 4 \cdot 5 \cdot 1}}{2 \cdot 5} \] \[ x = \frac{-6 \pm \sqrt{36 - 20}}{10} \] \[ x = \frac{-6 \pm \sqrt{16}}{10} \] \[ x = \frac{-6 \pm 4}{10} \]
- Calculate the two solutions: \[ x = \frac{-6 + 4}{10} = \frac{-2}{10} = -0.2 \] \[ x = \frac{-6 - 4}{10} = \frac{-10}{10} = -1 \]
Therefore, the solutions to the equation \(5x^2 + 6x + 1 = 0\) are \(x = -0.2\) and \(x = -1\).
Factoring Polynomials
Factoring polynomials involves rewriting a polynomial expression as the product of simpler polynomials. This process is essential for solving polynomial equations, simplifying expressions, and understanding polynomial functions. Here are the steps and methods commonly used to factor polynomials:
1. Factoring Out the Greatest Common Factor (GCF)
The first step in factoring any polynomial is to determine if there is a Greatest Common Factor (GCF) among the terms. The GCF is the largest factor that divides all terms of the polynomial.
- Identify the GCF of the coefficients.
- Identify the GCF of the variables.
- Combine these to find the GCF of the entire expression.
- Factor out the GCF from each term.
For example, to factor \(6x^3y^3 + 45x^2y^2 + 21xy\):
\[
\begin{align*}
GCF & = 3xy \\
6x^3y^3 + 45x^2y^2 + 21xy & = 3xy(2x^2y^2 + 15xy + 7)
\end{align*}
\]
2. Factoring Trinomials
Trinomials of the form \(ax^2 + bx + c\) can be factored by finding two numbers that multiply to \(ac\) and add to \(b\). For trinomials where \(a = 1\), this simplifies to finding two numbers that multiply to \(c\) and add to \(b\).
- Write the trinomial in standard form.
- Find two numbers that multiply to \(c\) and add to \(b\).
- Rewrite the middle term using these numbers and factor by grouping.
For example, to factor \(x^2 + 5x + 6\):
\[
x^2 + 5x + 6 = (x + 2)(x + 3)
\]
3. Factoring the Difference of Squares
Polynomials of the form \(a^2 - b^2\) can be factored using the identity:
\[
a^2 - b^2 = (a - b)(a + b)
\]
For example, to factor \(x^2 - 9\):
\[
x^2 - 9 = (x - 3)(x + 3)
\]
4. Factoring the Sum and Difference of Cubes
Polynomials of the form \(a^3 + b^3\) and \(a^3 - b^3\) can be factored using these identities:
\[
a^3 + b^3 = (a + b)(a^2 - ab + b^2)
\]
\[
a^3 - b^3 = (a - b)(a^2 + ab + b^2)
\]
For example, to factor \(27x^3 - y^3\):
\[
27x^3 - y^3 = (3x - y)(9x^2 + 3xy + y^2)
\]
5. Factoring by Grouping
When a polynomial has four or more terms, factoring by grouping can be useful. This involves grouping terms with common factors and factoring each group separately.
- Group terms with common factors.
- Factor out the GCF from each group.
- If done correctly, a common binomial factor should appear.
- Factor out the common binomial factor.
For example, to factor \(x^3 + 3x^2 + 2x + 6\):
\[
\begin{align*}
x^3 + 3x^2 + 2x + 6 & = (x^3 + 3x^2) + (2x + 6) \\
& = x^2(x + 3) + 2(x + 3) \\
& = (x^2 + 2)(x + 3)
\end{align*}
\]
6. Summary
To factor polynomials effectively, identify the type of polynomial and apply the appropriate method. Always start by factoring out the GCF, then use specific factoring techniques such as factoring trinomials, differences of squares, sums and differences of cubes, or factoring by grouping. Practice these methods to become proficient in simplifying polynomial expressions.
Using Online Calculators
Online calculators are powerful tools that can help you solve algebraic expressions, including those involving terms like \(3x + x^2\). Here's a step-by-step guide on how to use these calculators effectively:
-
Step 1: Choose a Reliable Online Calculator
There are many online calculators available, such as Symbolab, Mathway, and Desmos. These calculators offer a wide range of functionalities from basic arithmetic to complex algebraic equations.
- : Known for detailed step-by-step solutions.
- : Offers a versatile calculator for different types of math problems.
- : Excellent for graphing equations and visualizing solutions.
-
Step 2: Enter the Expression
Type your expression into the calculator. For example, to simplify \(3x + x^2\), you would input "3x + x^2" into the appropriate field. Make sure to use the correct syntax as specified by the calculator you are using.
-
Step 3: Submit the Expression
Click the submit or enter button to process the expression. The calculator will then provide the solution. Some calculators will show step-by-step solutions, which can be very helpful for understanding the process.
-
Step 4: Review the Solution
Review the solution provided by the calculator. For \(3x + x^2\), the output should confirm that the expression is already simplified. Use the step-by-step breakdown (if available) to understand how the solution was reached.
-
Step 5: Explore Additional Features
Many online calculators offer additional features such as graphing functions, solving equations, and factoring polynomials. Utilize these features to deepen your understanding and tackle more complex problems.
Using online calculators can greatly enhance your learning experience by providing instant feedback and detailed solutions. Make sure to explore the capabilities of each calculator and choose the one that best fits your needs.
Graphing Quadratic Functions
Graphing quadratic functions involves plotting parabolas, which are symmetrical curves that open either upwards or downwards. A quadratic function has the general form:
\( f(x) = ax^2 + bx + c \)
where \(a\), \(b\), and \(c\) are constants, and \(a \neq 0\).
Here is a step-by-step guide to graphing a quadratic function:
-
Determine the direction of the parabola: If \(a > 0\), the parabola opens upwards. If \(a < 0\), it opens downwards.
-
Find the axis of symmetry: The axis of symmetry is the vertical line that divides the parabola into two mirror images. It can be found using the formula:
\( x = -\frac{b}{2a} \) -
Locate the vertex: The vertex is the highest or lowest point on the graph. It lies on the axis of symmetry and can be found by substituting \( x \) from the axis of symmetry into the function:
\( f(h) = a(h)^2 + b(h) + c \)where \(h\) is the x-coordinate of the vertex. The vertex coordinates are \((h, k)\).
-
Find the y-intercept: The y-intercept is where the graph crosses the y-axis. This occurs when \( x = 0 \). Substitute \( x = 0 \) into the function to find the y-intercept:
\( f(0) = c \) -
Find the x-intercepts (if they exist): The x-intercepts are where the graph crosses the x-axis. These can be found by solving the quadratic equation \( f(x) = 0 \). This can be done using the quadratic formula:
\( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) -
Plot additional points: Choose x-values on either side of the vertex and calculate the corresponding y-values. Plot these points to ensure the graph is accurate.
-
Draw the parabola: Connect the points with a smooth curve to form the parabola, making sure it is symmetrical about the axis of symmetry.
By following these steps, you can accurately graph any quadratic function and understand its key features, such as the vertex, axis of symmetry, and intercepts.
Step-by-Step Problem Solving
Solving algebraic expressions step-by-step helps in understanding the process and ensures accuracy. Let's solve the expression \(3x + x^2\) by breaking it down into manageable steps.
- Identify the type of equation:
In this case, \(3x + x^2\) is a polynomial expression, specifically a quadratic equation since it includes a term with \(x^2\).
- Rearrange the equation (if necessary):
Ensure the equation is in the standard form \(ax^2 + bx + c = 0\). Here, it is already in this form with \(a = 1\), \(b = 3\), and \(c = 0\).
- Factor the quadratic expression:
To factor \(x^2 + 3x\), look for common factors in the terms. In this case, factor out \(x\):
\(x^2 + 3x = x(x + 3)\)
- Solve for the roots:
Set each factor equal to zero to solve for \(x\):
\(x = 0\) or \(x + 3 = 0\)
Therefore, \(x = 0\) or \(x = -3\).
- Verify the solutions:
Substitute the solutions back into the original equation to check:
- For \(x = 0\): \(3(0) + 0^2 = 0\) (True)
- For \(x = -3\): \(3(-3) + (-3)^2 = -9 + 9 = 0\) (True)
By following these steps, you can systematically solve the quadratic equation \(3x + x^2\) and verify the accuracy of your solutions. Online calculators and tools can assist with these steps, providing instant solutions and visual aids to enhance understanding.
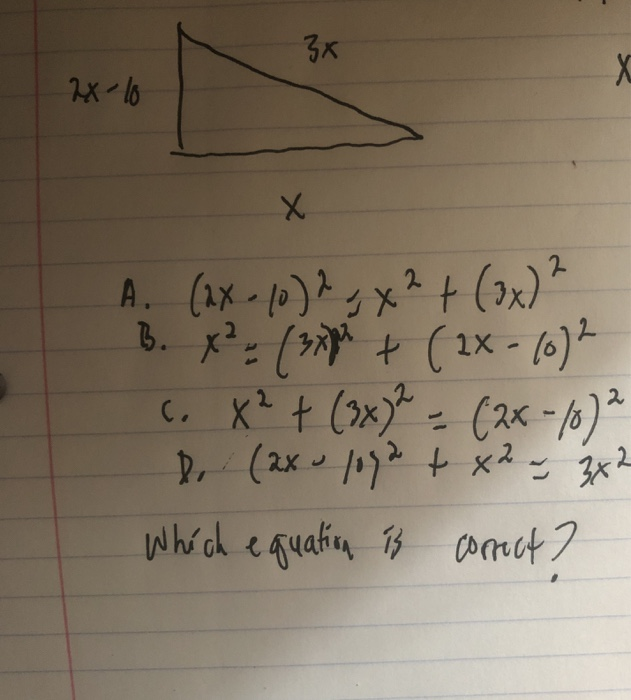
Applications in Real Life
Quadratic functions, such as 3x + x2, play a significant role in various real-life applications. Here are some common scenarios where these mathematical concepts are utilized:
- Projectile Motion: Quadratic equations are used to model the path of an object in projectile motion. The height of an object thrown into the air can be described by a quadratic equation, helping to predict its trajectory and impact point.
- Economics: In business and economics, quadratic functions can model cost and revenue functions to determine the maximum profit or minimum cost. For instance, the relationship between the quantity of a product produced and its total cost can often be expressed as a quadratic function.
- Engineering: Engineers use quadratic functions to design and analyze structures, such as bridges and buildings. The curves and parabolic shapes derived from quadratic equations ensure stability and strength in architectural designs.
- Astronomy: Quadratic equations help in calculating the orbits of celestial bodies. For example, predicting the return of Halley's Comet involves quadratic functions that approximate the comet's path around the sun.
- Biology: Growth rates of populations can be modeled using quadratic functions. For instance, the spread of certain diseases or the growth of animal populations in an ecosystem can be analyzed through quadratic models.
- Physics: Quadratic equations are essential in kinematics for solving problems involving acceleration, velocity, and displacement. They help in determining the motion parameters of objects under uniform acceleration.
Understanding the applications of quadratic functions enhances our ability to solve practical problems in various fields, making them a crucial part of mathematical studies.
Additional Resources
For further learning and practice on quadratic equations and algebraic expressions such as \(3x + x^2\), here are some valuable online resources:
- : This tool provides detailed step-by-step solutions to a wide variety of mathematical problems, including quadratic equations, factoring, and graphing.
- : A powerful computational engine that can solve equations, plot graphs, and offer insights into many mathematical concepts.
- : Comprehensive video tutorials and practice exercises covering algebraic expressions, quadratic equations, and more.
- : An easy-to-use calculator that provides solutions to a variety of algebraic problems, including detailed steps and explanations.
- : An intuitive graphing calculator that helps visualize quadratic functions and other algebraic expressions.
- : Offers lessons, practice problems, and strategies for understanding and solving algebraic equations.
These resources will help you deepen your understanding of algebraic concepts and provide tools to solve a variety of mathematical problems.
Phân tích đa thức x^2 - 3x + 2
READ MORE:
Cách Giải Phương Trình x^2 + 3x - 10 = 0 Bằng Phương Pháp Phân Tích

x-1=sec(squared)x.jpg)