Topic x squared times x squared: X squared times x squared is a fundamental algebraic expression that simplifies to x to the power of four. This article delves into the mathematical principles behind this simplification, offering clear explanations and examples to enhance your understanding of algebraic operations and exponent rules.
Table of Content
- Understanding "x squared times x squared"
- Introduction to Exponents
- Basics of Squaring Numbers
- Understanding x Squared
- Multiplication of Exponents
- Simplifying x Squared Times x Squared
- Examples and Applications
- Common Mistakes with Exponents
- Visualizing Perfect Squares
- Quadratic Equations and Their Solutions
- Using Online Calculators for Exponent Problems
- YOUTUBE: Tìm hiểu về phép nhân x với x trong đại số, x^2 hay 2x? Xem video để hiểu rõ hơn về khái niệm này.
Understanding "x squared times x squared"
When working with algebraic expressions, it's essential to understand how to multiply exponents correctly. Here, we will explore the calculation of "x squared times x squared".
Basic Concept
The expression "x squared" is written mathematically as \( x^2 \). To find "x squared times x squared", we use the properties of exponents.
According to the rules of exponents:
Therefore:
- \( x^2 \cdot x^2 = x^{2+2} = x^4 \)
Examples
| Expression | Result |
|---|---|
| \( x^2 \cdot x^2 \) | \( x^4 \) |
| \( y^3 \cdot y^3 \) | \( y^6 \) |
Visual Representation
Here's a visual representation of how the exponents add up:
\( (x \cdot x) \cdot (x \cdot x) = x^4 \)
Related Concepts
- The square root of \( x^2 \) is \( x \)
- \( x^2 \) is not the same as \( 2x \)
- The formula for the sum of squares: \( (a + b)^2 = a^2 + 2ab + b^2 \)
Applications
This concept is fundamental in algebra and is widely used in solving quadratic equations, simplifying expressions, and in various fields such as physics and engineering.
Conclusion
Understanding how to multiply exponents helps in simplifying complex algebraic expressions. By applying the rule \( x^m \cdot x^n = x^{m+n} \), we can easily solve "x squared times x squared" as \( x^4 \).

READ MORE:
Introduction to Exponents
Exponents are a fundamental concept in algebra that represent repeated multiplication of a number by itself. An exponent is written as a small number above and to the right of the base number. For example, \(x^2\) means \(x\) is multiplied by itself, resulting in \(x \times x\).
- Definition: The expression \(x^2\) is called "x squared," where \(x\) is the base and 2 is the exponent.
- Calculation: To find \(x^2\), multiply the base \(x\) by itself: \(x^2 = x \times x\).
Let's explore some key properties and operations involving exponents:
| Expression | Explanation |
| \(x^2\) | \(x\) multiplied by itself: \(x \times x\). |
| \(x^2 \times x^2\) | Equals \(x\) to the power of 4: \(x^2 \times x^2 = x^4\). |
| \(\sqrt{x^2}\) | The square root of \(x^2\) is \(x\): \(\sqrt{x^2} = x\). |
| \((a + b)^2\) | Expands to \(a^2 + 2ab + b^2\): \((a + b)^2 = (a + b)(a + b)\). |
| \((a - b)^2\) | Expands to \(a^2 - 2ab + b^2\): \((a - b)^2 = (a - b)(a - b)\). |
Exponents are also involved in various algebraic expressions and equations. For example:
- \(x^2 + x^2 = 2x^2\): Adding like terms with the same exponent.
- \((x^2 - y^2) = (x + y)(x - y)\): The difference of squares formula.
Understanding exponents is crucial for solving algebraic problems and simplifying expressions. They form the basis for more advanced mathematical concepts and operations.
Basics of Squaring Numbers
Squaring a number means multiplying the number by itself. For example, squaring the number 3 involves calculating \(3 \times 3\), which equals 9. In mathematical notation, this is written as \(3^2 = 9\).
Here are the basic steps to understand squaring numbers:
- Identify the base: The number to be squared is known as the base. For example, in \(x^2\), x is the base.
- Multiply the base by itself: To square the base, multiply it by itself. This can be expressed as \(x \times x = x^2\).
- Apply exponent rules: When multiplying exponents with the same base, add the exponents. For example, \(x^2 \times x^2 = x^{2+2} = x^4\).
Squaring numbers is fundamental in algebra and is used in various mathematical and scientific fields. It forms the basis for more advanced operations like solving quadratic equations, working with polynomials, and understanding geometric concepts like the area of squares.
Let's look at a few examples:
| Expression | Calculation | Result |
|---|---|---|
| \(4^2\) | \(4 \times 4\) | 16 |
| \(5^2\) | \(5 \times 5\) | 25 |
| \((x+2)^2\) | \((x+2) \times (x+2)\) | \(x^2 + 4x + 4\) |
Understanding these basics will help in tackling more complex mathematical problems and applications in physics, engineering, and computer science.
Understanding x Squared
In mathematics, squaring a number means multiplying it by itself. The notation \( x^2 \) signifies \( x \) multiplied by \( x \). This concept is fundamental in algebra and has wide applications in various fields of mathematics.
To understand \( x^2 \), consider the following properties:
- \( x^2 \) is always non-negative because a positive or negative number squared results in a positive product.
- When \( x = 0 \), \( x^2 = 0 \).
- The square of a number grows quadratically, which means it increases rapidly as the value of \( x \) increases.
Let's explore an example:
| If \( x = 3 \): | \( x^2 = 3^2 = 3 \times 3 = 9 \) |
| If \( x = -4 \): | \( x^2 = (-4)^2 = (-4) \times (-4) = 16 \) |
We can also multiply squares together. For instance, \( x^2 \times x^2 = (x \times x) \times (x \times x) = x^4 \). This illustrates how the exponent rules apply when multiplying like bases.
Understanding \( x^2 \) is essential for solving quadratic equations, analyzing parabolas, and many other mathematical concepts. Mastery of this fundamental operation opens the door to more advanced topics in algebra and calculus.
Multiplication of Exponents
Multiplying exponents involves using the laws of exponents to simplify expressions. This is particularly useful when dealing with powers of the same base.
For example, let's consider the expression \(x^2 \times x^2\). Here's a detailed step-by-step process to understand this multiplication:
- Step 1: Identify the bases and exponents in the expression.
- Step 2: Since the bases are the same (both are \(x\)), you can add the exponents.
- Step 3: Add the exponents: \(2 + 2 = 4\).
- Step 4: Write the result as \(x^4\).
Thus, \(x^2 \times x^2 = x^4\).
Here is another example to further clarify:
- Example: \(a^3 \times a^5\)
- Step 1: Identify the bases and exponents.
- Step 2: Since the bases are the same (both are \(a\)), you can add the exponents.
- Step 3: Add the exponents: \(3 + 5 = 8\).
- Step 4: Write the result as \(a^8\).
So, \(a^3 \times a^5 = a^8\).
This rule applies to any expression where you multiply powers of the same base. It's a fundamental concept in algebra that helps simplify complex expressions efficiently.
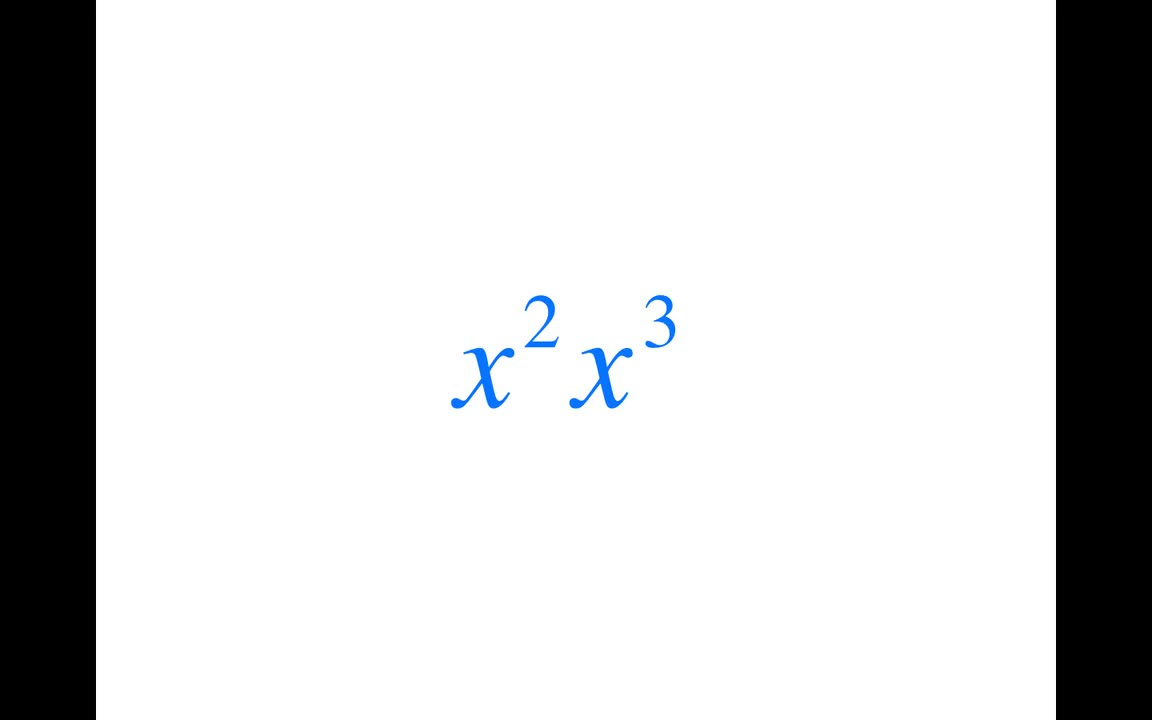
Simplifying x Squared Times x Squared
The process of simplifying \(x^2 \times x^2\) involves understanding the basic rules of exponents. When you multiply terms with the same base, you add their exponents. Here's a step-by-step guide:
- Identify the Base and Exponents: In \(x^2 \times x^2\), the base is \(x\) and the exponents are both 2.
- Add the Exponents: Using the rule \(a^m \times a^n = a^{m+n}\), add the exponents: \(2 + 2 = 4\).
- Simplify the Expression: This gives you \(x^{2+2} = x^4\).
Therefore, \(x^2 \times x^2\) simplifies to \(x^4\). This rule applies to any similar expressions where you are multiplying terms with the same base.
Here's a summary in table format for better understanding:
| Expression | Steps | Result |
|---|---|---|
| \(x^2 \times x^2\) | Identify base (x) and exponents (2, 2) | \(x^{2+2}\) |
| Add exponents: \(2 + 2 = 4\) | \(x^4\) |
This method is a fundamental principle of algebra and helps in simplifying polynomial expressions efficiently.
Examples and Applications
The multiplication of exponents is a fundamental concept in algebra, particularly useful in various mathematical and real-world applications. Below are some detailed examples and applications of the expression \( x^2 \times x^2 \), which simplifies to \( x^4 \) using the rule \( x^m \times x^n = x^{m+n} \).
Examples
-
Basic Algebraic Example:
Consider the expression \( x^2 \times x^2 \). By applying the exponent rule:
\[ x^2 \times x^2 = x^{2+2} = x^4 \]
This shows how the product of two squared terms results in a term raised to the fourth power.
-
Numeric Example:
For a specific value, let \( x = 3 \). Then:
\[ (3^2) \times (3^2) = 9 \times 9 = 81 \]
Alternatively, directly using the simplified form:
\[ 3^4 = 81 \]
This confirms that \( x^2 \times x^2 = x^4 \).
Applications
-
Geometry and Area Calculation:
In geometry, squaring a term is often used to calculate areas. For example, if the side of a square is \( x \), the area is \( x^2 \). If two such squares are combined multiplicatively, the resulting area is:
\[ x^2 \times x^2 = x^4 \]
This might represent a higher-dimensional analog or a compound area calculation.
-
Physics - Kinematic Equations:
In physics, particularly in kinematics, squared terms often appear in equations of motion. For instance, the displacement \( s \) in uniformly accelerated motion is given by:
\[ s = ut + \frac{1}{2}at^2 \]
If we need to find the combined effect of two such displacements where \( t \) is squared, the multiplication of two such terms would involve:
\[ (ut + \frac{1}{2}at^2) \times (ut + \frac{1}{2}at^2) \]
Which, after expansion, includes terms like \( t^4 \).
-
Economics - Compound Interest:
In economics, the formula for compound interest involves exponentiation. If the interest is compounded annually, the amount \( A \) after \( t \) years is:
\[ A = P(1 + r)^t \]
When considering compound interest over multiple periods, exponents are multiplied, which can be expressed using \( x^2 \times x^2 \) type of operations.
These examples and applications demonstrate how the principles of exponents, particularly the multiplication of squared terms, are applied in various mathematical and practical contexts, reinforcing the importance of understanding \( x^2 \times x^2 \) as \( x^4 \).
Common Mistakes with Exponents
When working with exponents, there are several common mistakes that students often make. Understanding these errors can help in avoiding them and mastering the correct application of exponent rules. Below are some of the typical mistakes along with explanations and correct methods:
1. Incorrect Application of the Product Rule
The product rule states that when multiplying like bases, you add the exponents: \( a^m \cdot a^n = a^{m+n} \). A common mistake is to multiply the exponents instead of adding them.
- Incorrect: \( x^2 \cdot x^3 = x^6 \)
- Correct: \( x^2 \cdot x^3 = x^{2+3} = x^5 \)
2. Misunderstanding the Power of a Power Rule
The power rule states that when raising an exponent to another power, you multiply the exponents: \( (a^m)^n = a^{m \cdot n} \). A common error is to add the exponents instead of multiplying them.
- Incorrect: \( (x^2)^3 = x^{2+3} = x^5 \)
- Correct: \( (x^2)^3 = x^{2 \cdot 3} = x^6 \)
3. Distributing Exponents over Addition
Exponents do not distribute over addition. This is a frequent mistake where students incorrectly apply the exponent to each term inside the parentheses.
- Incorrect: \( (a + b)^2 = a^2 + b^2 \)
- Correct: \( (a + b)^2 = (a + b)(a + b) = a^2 + 2ab + b^2 \)
4. Confusing the Quotient Rule
The quotient rule states that when dividing like bases, you subtract the exponents: \( \frac{a^m}{a^n} = a^{m-n} \). Students often mistakenly divide the exponents instead of subtracting them.
- Incorrect: \( \frac{x^5}{x^2} = x^{5/2} \)
- Correct: \( \frac{x^5}{x^2} = x^{5-2} = x^3 \)
5. Zero Exponent Misconceptions
Any base raised to the power of zero is one: \( a^0 = 1 \). A common mistake is to assume the result is zero.
- Incorrect: \( 5^0 = 0 \)
- Correct: \( 5^0 = 1 \)
6. Negative Exponents
Negative exponents represent the reciprocal of the base raised to the positive exponent: \( a^{-n} = \frac{1}{a^n} \). Students often neglect this reciprocal relationship.
- Incorrect: \( 2^{-3} = -8 \)
- Correct: \( 2^{-3} = \frac{1}{2^3} = \frac{1}{8} \)
7. Handling Complex Expressions
In more complex expressions, students often fail to correctly apply multiple exponent rules simultaneously.
- Example: Simplify \( \left(\frac{x^3 \cdot y^{-2}}{z^4}\right)^2 \)
- Solution: \( \left(\frac{x^3 \cdot y^{-2}}{z^4}\right)^2 = \frac{(x^3)^2 \cdot (y^{-2})^2}{(z^4)^2} = \frac{x^6 \cdot y^{-4}}{z^8} \)
By recognizing and understanding these common mistakes, students can improve their proficiency with exponents and ensure accurate calculations.
Visualizing Perfect Squares
Visualizing perfect squares can help in understanding how squaring a number relates to area and how multiplying exponents works. Let's explore this concept step-by-step with some examples and visual aids.
Definition of Perfect Squares:
A perfect square is a number that can be expressed as the product of an integer with itself. For example, \(4\) is a perfect square because it is \(2 \times 2\). In algebraic terms, \(x^2\) represents a perfect square.
Geometric Interpretation:
Consider a square with a side length of \(x\). The area of this square is \(x^2\), which represents the perfect square geometrically. When we multiply \(x^2\) by itself, we get \(x^4\), which can be visualized as a square of side length \(x^2\).
| Side Length | Area | Visualization |
|---|---|---|
| \(x\) | \(x^2\) |

|
| \(x^2\) | \(x^4\) |
Example with Numbers:
Let's take \(x = 3\). The perfect square is \(3^2 = 9\). If we square this result, we get \(9^2 = 81\). This means that the side length of the new square is \(9\) and the area is \(81\).
Algebraic Visualization:
In algebraic terms, if we have \(x^2\) and multiply it by itself:
\[
x^2 \times x^2 = x^{2+2} = x^4
\]
This is the basis for understanding higher powers and visualizing exponential growth.
Interactive Tools:
Using online graphing tools or math software can help in visualizing these concepts. For example, plotting the function \(y = x^2\) and then \(y = x^4\) can show how the area grows exponentially.
Understanding perfect squares through visualization aids in grasping more complex algebraic concepts and applying them effectively in problem-solving.
Quadratic Equations and Their Solutions
Quadratic equations are polynomial equations of the form \( ax^2 + bx + c = 0 \), where \( a \neq 0 \). These equations can have two, one, or no real solutions. Let's explore the different methods to solve quadratic equations and some examples.
Methods to Solve Quadratic Equations
- Factoring: Express the quadratic equation in factored form.
- Using the Quadratic Formula: Apply the formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \).
- Completing the Square: Rewrite the equation in the form \( (x - p)^2 = q \) and solve for \( x \).
- Graphing: Plot the quadratic function and find the x-intercepts.
Example 1: Solving by Factoring
Solve \( x^2 + 5x + 6 = 0 \).
- Rewrite the equation: \( x^2 + 5x + 6 = 0 \).
- Factor the quadratic: \( (x + 2)(x + 3) = 0 \).
- Set each factor to zero: \( x + 2 = 0 \) and \( x + 3 = 0 \).
- Solve for \( x \): \( x = -2 \) and \( x = -3 \).
Example 2: Using the Quadratic Formula
Solve \( 5x^2 + 6x + 1 = 0 \).
- Identify coefficients: \( a = 5 \), \( b = 6 \), \( c = 1 \).
- Apply the quadratic formula: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
- Substitute \( a \), \( b \), and \( c \) into the formula: \[ x = \frac{-6 \pm \sqrt{6^2 - 4 \cdot 5 \cdot 1}}{2 \cdot 5} = \frac{-6 \pm \sqrt{36 - 20}}{10} = \frac{-6 \pm \sqrt{16}}{10} \]
- Simplify under the square root: \[ x = \frac{-6 \pm 4}{10} \]
- Find the two solutions: \[ x = \frac{-6 + 4}{10} = -0.2 \quad \text{and} \quad x = \frac{-6 - 4}{10} = -1 \]
Example 3: Completing the Square
Solve \( x^2 + 6x + 9 = 0 \).
- Rewrite the equation: \( x^2 + 6x + 9 = 0 \).
- Complete the square: \[ x^2 + 6x + 9 = (x + 3)^2 \]
- Set the equation to zero: \[ (x + 3)^2 = 0 \]
- Solve for \( x \): \[ x + 3 = 0 \quad \Rightarrow \quad x = -3 \]
Understanding the Discriminant
The discriminant of a quadratic equation \( b^2 - 4ac \) determines the nature of the roots:
- If \( b^2 - 4ac > 0 \): Two distinct real solutions.
- If \( b^2 - 4ac = 0 \): One real solution (a repeated root).
- If \( b^2 - 4ac < 0 \): Two complex solutions.
Example 4: Using the Discriminant
Solve \( x^2 + 4x + 5 = 0 \).
- Identify coefficients: \( a = 1 \), \( b = 4 \), \( c = 5 \).
- Calculate the discriminant: \[ \Delta = b^2 - 4ac = 4^2 - 4 \cdot 1 \cdot 5 = 16 - 20 = -4 \]
- Since \( \Delta < 0 \), there are two complex solutions.
- Apply the quadratic formula with complex numbers: \[ x = \frac{-4 \pm \sqrt{-4}}{2 \cdot 1} = \frac{-4 \pm 2i}{2} = -2 \pm i \]
Using Online Calculators for Exponent Problems
Online calculators are valuable tools for simplifying and solving exponent problems. Here are steps to effectively use them:
- Choose the Right Calculator: There are many online calculators available, such as Mathway, Symbolab, and Omni Calculator. Each has specific features suitable for different types of exponent problems.
- Input the Problem: Enter the exponential expression you want to solve. For example, if you want to simplify
x^2 \cdot x^2, you would input it asx^2 * x^2. - Select the Operation: Choose the appropriate function for your calculation. Most calculators will have options like "Simplify", "Multiply", or "Exponentiation". For instance, in Symbolab, you would select the "Simplify" option.
- Review the Steps: These calculators not only provide the answer but also show the step-by-step process. This helps in understanding the underlying principles, such as the product of powers rule:
(x^a) \cdot (x^b) = x^{a+b}. - Advanced Features: Many calculators offer advanced features, such as handling negative exponents, fractional exponents, and providing decimal approximations. Exploring these can deepen your understanding and assist with more complex problems.
Here is an example using Symbolab's Exponent Calculator:
- Input:
x^2 \cdot x^2 - Step-by-Step Solution:
- Apply the product of powers rule:
x^2 \cdot x^2 = x^{2+2} - Simplify the exponent:
x^{2+2} = x^4
- Apply the product of powers rule:
- Result:
x^4
Using these calculators effectively can save time and improve accuracy when dealing with exponent problems.
Tìm hiểu về phép nhân x với x trong đại số, x^2 hay 2x? Xem video để hiểu rõ hơn về khái niệm này.
x Nhân x Trong Đại Số Là Gì? (x^2 hay 2x)
READ MORE:
Video này giải thích sự khác biệt giữa âm của x bình phương và bình phương của âm x, giúp bạn hiểu rõ hơn về khái niệm toán học này.
Sự khác biệt giữa âm của x bình phương và bình phương của âm x


x-1=sec(squared)x.jpg)









