Topic i squared equals: Discover the fascinating world of imaginary numbers with our in-depth exploration of "i squared equals." This article delves into the significance of i squared, its historical context, practical applications, and its role in complex mathematical theories. Join us on a journey to understand how this concept impacts various fields, from engineering to quantum physics.
Table of Content
- Understanding i2
- Introduction to Imaginary Numbers
- The Definition of i
- Understanding i Squared Equals -i
- Historical Context of Imaginary Numbers
- Applications of Imaginary Numbers in Various Fields
- Complex Numbers: A Combination of Real and Imaginary Parts
- Graphical Representation of Complex Numbers
- Operations with Complex Numbers
- Addition and Subtraction of Complex Numbers
- Multiplication and Division of Complex Numbers
- Polar Form and Exponential Form of Complex Numbers
- The Role of i in Quadratic Equations
- Engineering Applications of Complex Numbers
- Complex Numbers in Electrical Engineering
- Complex Numbers in Signal Processing
- Use of Imaginary Numbers in Quantum Physics
- Advanced Mathematical Theories Involving i
- Euler's Formula and its Implications
- YOUTUBE: Hướng dẫn chi tiết cách sử dụng số phức i bình phương trong toán học, giúp bạn hiểu rõ hơn về khái niệm và ứng dụng của i bình phương.
Understanding i2
The expression i2 commonly appears in mathematics, particularly in the context of complex numbers. In complex number theory, i represents the imaginary unit, which is defined as the square root of -1. This means:
When i is squared, the result is -1:
Properties and Uses of i2
- Imaginary Numbers: The number i is essential in defining imaginary numbers, which are used in complex number systems.
- Complex Numbers: Complex numbers combine real and imaginary parts and are written in the form a + bi.
- Quadratic Equations: i2 is used to find solutions to quadratic equations that do not have real roots.
- Electromagnetic Theory: i is often used in electrical engineering to represent phase differences in alternating current circuits.
Visual Representation
The imaginary unit i can be represented graphically on the complex plane:
| Axis | Representation |
|---|---|
| Real Axis | Horizontal line |
| Imaginary Axis | Vertical line |
A point on the complex plane represents a complex number, with the x-coordinate as the real part and the y-coordinate as the imaginary part.
Further Reading

READ MORE:
Introduction to Imaginary Numbers
Imaginary numbers are an essential concept in mathematics, often used to solve equations that do not have real number solutions. The imaginary unit is denoted by \(i\), where \(i\) is defined as the square root of \(-1\). This means:
\[
i^2 = -1
\]
Imaginary numbers extend the real number system \( \mathbb{R} \) to the complex number system \( \mathbb{C} \), allowing for a broader range of mathematical solutions. Here are some key points to understand about imaginary numbers:
- The number \(i\) is not a real number, as no real number squared equals \(-1\).
- Imaginary numbers can be added, subtracted, multiplied, and divided just like real numbers, but with special rules for \(i\).
- Complex numbers are formed by combining real and imaginary numbers in the form \(a + bi\), where \(a\) and \(b\) are real numbers.
Let's explore the basic operations involving imaginary numbers:
- Addition and Subtraction: Combine like terms (real with real, imaginary with imaginary). For example: \[ (3 + 2i) + (1 + 4i) = 4 + 6i \]
- Multiplication: Use the distributive property and apply \(i^2 = -1\). For example: \[ (2 + 3i)(1 + 4i) = 2 + 8i + 3i + 12i^2 = 2 + 11i - 12 = -10 + 11i \]
- Division: Multiply the numerator and the denominator by the conjugate of the denominator. For example: \[ \frac{3 + 2i}{1 - i} \times \frac{1 + i}{1 + i} = \frac{(3 + 2i)(1 + i)}{(1 - i)(1 + i)} = \frac{3 + 3i + 2i + 2i^2}{1 - i^2} = \frac{3 + 5i - 2}{1 + 1} = \frac{1 + 5i}{2} = \frac{1}{2} + \frac{5}{2}i \]
Understanding imaginary numbers and their operations is crucial for progressing in higher-level mathematics and various applications in science and engineering.
The Definition of i
In mathematics, the symbol \(i\) represents the imaginary unit, which is defined as the square root of \(-1\). This fundamental concept in the field of complex numbers allows for the extension of the real number system. The defining property of \(i\) is:
\[
i^2 = -1
\]
This definition is not intuitive within the realm of real numbers, as no real number squared gives a negative result. Imaginary numbers provide a way to handle such situations, expanding our ability to solve various mathematical problems. Here are the key aspects of the definition of \(i\):
- \(\sqrt{-1} = i\): By definition, \(i\) is the number that satisfies this equation.
- \(i^2 = -1\): This is the fundamental property that all imaginary numbers are based on.
- Negative roots: \(i\) allows us to take square roots of negative numbers. For example: \[ \sqrt{-4} = \sqrt{4 \cdot -1} = \sqrt{4} \cdot \sqrt{-1} = 2i \]
Imaginary numbers are often combined with real numbers to form complex numbers, which are written in the form \(a + bi\), where \(a\) and \(b\) are real numbers. Here are some operations involving \(i\):
- Addition and Subtraction: Treat \(i\) as a variable and combine like terms. \[ (3 + 2i) + (1 + 4i) = 4 + 6i \]
- Multiplication: Apply the distributive property and use \(i^2 = -1\). \[ (1 + 2i)(3 + 4i) = 1 \cdot 3 + 1 \cdot 4i + 2i \cdot 3 + 2i \cdot 4i = 3 + 4i + 6i + 8i^2 = 3 + 10i - 8 = -5 + 10i \]
- Division: Multiply the numerator and denominator by the conjugate of the denominator. \[ \frac{2 + 3i}{1 - 4i} \times \frac{1 + 4i}{1 + 4i} = \frac{(2 + 3i)(1 + 4i)}{(1 - 4i)(1 + 4i)} = \frac{2 + 8i + 3i + 12i^2}{1 - 16i^2} = \frac{2 + 11i - 12}{1 + 16} = \frac{-10 + 11i}{17} = -\frac{10}{17} + \frac{11}{17}i \]
The definition of \(i\) is pivotal in advancing from real numbers to complex numbers, thus enabling the solution of a wider array of mathematical equations and problems.
Understanding i Squared Equals -i
Imaginary numbers extend the real number system to complex numbers, enabling solutions to equations that involve square roots of negative numbers. The imaginary unit \(i\) is defined as \(i = \sqrt{-1}\). One of its fundamental properties is:
\[
i^2 = -1
\]
This equation signifies that squaring the imaginary unit results in \(-1\). This is a crucial aspect of complex numbers, forming the basis for further operations. Let's delve deeper into understanding \(i^2 = -1\) and its implications:
- Basic Definition: By definition, \(i\) is the square root of \(-1\). Hence, \[ i^2 = (\sqrt{-1})^2 = -1 \]
- Complex Number Formation: Combining real numbers with imaginary numbers forms complex numbers: \[ z = a + bi \] where \(a\) and \(b\) are real numbers. The operations on these numbers rely on the property \(i^2 = -1\).
- Operations Involving \(i\): Let's explore some examples to solidify our understanding:
- Multiplication: When multiplying complex numbers, the property \(i^2 = -1\) is often used. \[ (2 + 3i)(4 + 5i) = 2 \cdot 4 + 2 \cdot 5i + 3i \cdot 4 + 3i \cdot 5i = 8 + 10i + 12i + 15i^2 = 8 + 22i - 15 = -7 + 22i \]
- Powers of \(i\): Higher powers of \(i\) cycle through a pattern due to \(i^2 = -1\):
- \(i^1 = i\)
- \(i^2 = -1\)
- \(i^3 = i \cdot i^2 = i \cdot -1 = -i\)
- \(i^4 = (i^2)^2 = (-1)^2 = 1\)
- \(i^5 = i\)
- ... and so on, repeating every four powers.
- Application in Equations: Using \(i^2 = -1\) helps solve quadratic equations with negative discriminants: \[ x^2 + 1 = 0 \implies x^2 = -1 \implies x = \pm i \]
In conclusion, understanding \(i^2 = -1\) is fundamental to working with imaginary and complex numbers, enabling a broader range of mathematical solutions and applications.
Historical Context of Imaginary Numbers
The concept of imaginary numbers has a rich and intriguing history, stretching back centuries and evolving through the contributions of numerous mathematicians. Here is a detailed exploration of the historical context of imaginary numbers:
- Early Beginnings: The notion of imaginary numbers emerged in the 16th century during attempts to solve cubic equations. Mathematicians encountered the square roots of negative numbers, which puzzled them. The Italian mathematician Gerolamo Cardano was one of the first to introduce these numbers in his work "Ars Magna" (1545), although he did not fully understand them.
- Development of the Concept: In the 17th century, Rafael Bombelli made significant strides in formalizing imaginary numbers. He developed rules for manipulating these numbers, laying the groundwork for future advancements. His book "Algebra" (1572) was pivotal in recognizing and working with complex numbers.
- Acceptance and Further Exploration: The 18th century saw further developments, with mathematicians like John Wallis and Isaac Newton acknowledging the existence of imaginary numbers. However, it was not until the work of Leonhard Euler and Carl Friedrich Gauss in the 18th and 19th centuries that imaginary numbers gained widespread acceptance. Euler introduced the notation \(i\) for \(\sqrt{-1}\), while Gauss provided a comprehensive framework for complex numbers, including their geometric representation.
- Geometric Interpretation: Gauss's work was instrumental in visualizing complex numbers as points in a plane, now known as the complex plane or Argand plane. This geometric interpretation helped demystify imaginary numbers and made them more accessible to mathematicians and scientists.
- Modern Developments: In the 19th and 20th centuries, the theory of complex numbers continued to evolve, finding applications in various fields such as engineering, physics, and computer science. Mathematicians like Augustin-Louis Cauchy and Bernhard Riemann contributed to the development of complex analysis, a branch of mathematics focused on functions of complex variables.
The journey of imaginary numbers from a puzzling concept to a fundamental component of modern mathematics highlights the importance of theoretical exploration and the evolution of mathematical ideas. Today, imaginary numbers are integral to many scientific and engineering disciplines, demonstrating their enduring significance.
Applications of Imaginary Numbers in Various Fields
Imaginary numbers, and more broadly complex numbers, play a crucial role in various fields of science, engineering, and technology. Their applications extend far beyond pure mathematics, impacting several practical and theoretical domains. Here are some key areas where imaginary numbers are applied:
- Electrical Engineering:
In electrical engineering, complex numbers are used to analyze and design alternating current (AC) circuits. Impedance, which combines resistance and reactance, is expressed as a complex number:
\[
Z = R + jX
\]
where \(R\) is resistance, \(X\) is reactance, and \(j\) is the imaginary unit. This allows engineers to easily calculate voltages, currents, and power in AC circuits using complex arithmetic. - Signal Processing:
Imaginary numbers are essential in signal processing, particularly in the context of Fourier transforms. The Fourier transform decomposes signals into their frequency components, represented as complex numbers. This is fundamental for analyzing and filtering signals in various applications such as audio processing, telecommunications, and image compression.
- Quantum Mechanics:
In quantum mechanics, complex numbers are intrinsic to the mathematical formulation of quantum states and operators. The Schrödinger equation, which describes how the quantum state of a physical system changes over time, is expressed using complex wave functions:
\[
i\hbar \frac{\partial \psi}{\partial t} = \hat{H} \psi
\]
where \(\psi\) is the wave function, \(i\) is the imaginary unit, \(\hbar\) is the reduced Planck constant, and \(\hat{H}\) is the Hamiltonian operator. - Control Theory:
In control theory, complex numbers are used to analyze and design control systems. The stability and response of control systems are often evaluated using the poles and zeros of their transfer functions, which are complex numbers. This helps in designing systems that meet desired performance criteria.
- Fluid Dynamics:
Complex potential theory in fluid dynamics uses complex numbers to simplify the analysis of two-dimensional, incompressible, and irrotational flow fields. The complex potential function, which combines the velocity potential and stream function, facilitates solving problems related to fluid flow around objects.
- Economics and Finance:
In economics and finance, complex numbers are applied in certain models to represent oscillatory behaviors and cycles. For instance, they can be used in the analysis of cyclical trends in markets and in the study of certain dynamic systems within economic theories.
The versatility of imaginary numbers demonstrates their profound impact across multiple disciplines. Their ability to simplify and solve complex problems makes them indispensable tools in modern science and engineering.
Complex Numbers: A Combination of Real and Imaginary Parts
Complex numbers are a fundamental concept in mathematics, formed by combining real and imaginary numbers. They extend the real number system, enabling solutions to a wider range of mathematical problems. A complex number is typically written in the form:
\[
z = a + bi
\]
where \(a\) and \(b\) are real numbers, and \(i\) is the imaginary unit with the property \(i^2 = -1\).
Here is a detailed exploration of complex numbers and their properties:
- Real and Imaginary Parts:
In the complex number \(z = a + bi\), \(a\) is called the real part, and \(b\) is called the imaginary part. These can be extracted using:
\[
\text{Re}(z) = a \quad \text{and} \quad \text{Im}(z) = b
\] - Arithmetic Operations:
Complex numbers can be added, subtracted, multiplied, and divided using specific rules. Consider two complex numbers \(z_1 = a + bi\) and \(z_2 = c + di\):
- Addition:
\[
z_1 + z_2 = (a + c) + (b + d)i
\]
- Subtraction:
\[
z_1 - z_2 = (a - c) + (b - d)i
\]
- Multiplication:
\[
z_1 \cdot z_2 = (a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i
\]
(using \(i^2 = -1\))
- Division:
To divide \(z_1\) by \(z_2\), multiply the numerator and denominator by the conjugate of the denominator:
\[
\frac{z_1}{z_2} = \frac{a + bi}{c + di} \cdot \frac{c - di}{c - di} = \frac{(a + bi)(c - di)}{c^2 + d^2} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2}
\]
- Addition:
- Conjugate and Modulus:
The conjugate of a complex number \(z = a + bi\) is denoted as \(\overline{z}\) and is defined as:
\[
\overline{z} = a - bi
\]
The modulus (or absolute value) of \(z\) is given by:
\[
|z| = \sqrt{a^2 + b^2}
\]
The modulus represents the distance of the complex number from the origin in the complex plane. - Polar Form:
Complex numbers can also be represented in polar form as:
\[
z = r(\cos \theta + i \sin \theta) = re^{i\theta}
\]
where \(r = |z|\) is the modulus and \(\theta = \arg(z)\) is the argument of the complex number.
Understanding complex numbers and their operations is essential in various fields, including engineering, physics, and applied mathematics. Their unique properties and representations provide powerful tools for solving complex equations and modeling real-world phenomena.
Graphical Representation of Complex Numbers
Complex numbers can be visualized graphically using the complex plane, also known as the Argand plane. This representation provides an intuitive way to understand the properties and operations of complex numbers. The complex plane is a two-dimensional plane where the horizontal axis represents the real part and the vertical axis represents the imaginary part of a complex number. Let's explore this in detail:
- Plotting Complex Numbers:
A complex number \( z = a + bi \) can be represented as a point \((a, b)\) in the complex plane. Here, \(a\) is the real part, and \(b\) is the imaginary part. For example, the complex number \(3 + 4i\) is plotted at the point \((3, 4)\).
- Geometric Interpretation:
In the complex plane, the distance of a complex number from the origin (0, 0) is called its modulus, and it is denoted as \( |z| \). The modulus of \( z = a + bi \) is given by:
\[
|z| = \sqrt{a^2 + b^2}
\]
The angle \( \theta \) that the line segment from the origin to the point \( (a, b) \) makes with the positive real axis is called the argument of \( z \), denoted as \( \arg(z) \). - Polar Form:
A complex number can also be expressed in polar form as:
\[
z = r(\cos \theta + i \sin \theta)
\]
where \( r = |z| \) is the modulus and \( \theta = \arg(z) \) is the argument. Using Euler's formula, this can be written as:
\[
z = re^{i\theta}
\]
This form is particularly useful for multiplying and dividing complex numbers. - Operations in the Complex Plane:
- Addition:
To add two complex numbers \( z_1 = a + bi \) and \( z_2 = c + di \), plot both numbers as points and then form a parallelogram. The sum \( z_1 + z_2 \) is the diagonal of the parallelogram starting from the origin:
\[
(a + c) + (b + d)i
\] - Multiplication:
To multiply two complex numbers, multiply their moduli and add their arguments. If \( z_1 = r_1 e^{i \theta_1} \) and \( z_2 = r_2 e^{i \theta_2} \), then:
\[
z_1 \cdot z_2 = r_1 r_2 e^{i (\theta_1 + \theta_2)}
\] - Conjugation:
The conjugate of a complex number \( z = a + bi \) is \( \overline{z} = a - bi \). In the complex plane, this reflects the point \( (a, b) \) across the real axis to \( (a, -b) \).
- Addition:
The graphical representation of complex numbers in the complex plane is a powerful tool for visualizing and understanding their properties and operations. This geometric perspective simplifies many aspects of complex number theory and is widely used in various mathematical and engineering applications.
Operations with Complex Numbers
Complex numbers, represented as \(z = a + bi\) where \(a\) is the real part and \(b\) is the imaginary part, follow specific rules for arithmetic operations. Understanding these operations is essential for working with complex numbers in various mathematical and engineering contexts. Here, we detail the key operations step by step:
- Addition:
To add two complex numbers, add their real parts and their imaginary parts separately. Let \(z_1 = a + bi\) and \(z_2 = c + di\), then:
\[
z_1 + z_2 = (a + c) + (b + d)i
\]
Example: \((3 + 4i) + (1 + 2i) = (3 + 1) + (4 + 2)i = 4 + 6i\). - Subtraction:
To subtract one complex number from another, subtract their real parts and their imaginary parts separately. Let \(z_1 = a + bi\) and \(z_2 = c + di\), then:
\[
z_1 - z_2 = (a - c) + (b - d)i
\]
Example: \((3 + 4i) - (1 + 2i) = (3 - 1) + (4 - 2)i = 2 + 2i\). - Multiplication:
To multiply two complex numbers, use the distributive property and apply \(i^2 = -1\). Let \(z_1 = a + bi\) and \(z_2 = c + di\), then:
\[
z_1 \cdot z_2 = (a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i
\]
Example: \((3 + 4i)(1 + 2i) = 3 \cdot 1 + 3 \cdot 2i + 4i \cdot 1 + 4i \cdot 2i = 3 + 6i + 4i + 8i^2 = 3 + 10i - 8 = -5 + 10i\). - Division:
To divide one complex number by another, multiply the numerator and the denominator by the conjugate of the denominator. Let \(z_1 = a + bi\) and \(z_2 = c + di\), then:
- Step 1: Find the conjugate of the denominator \(z_2\), which is \( \overline{z_2} = c - di \).
- Step 2: Multiply the numerator and the denominator by the conjugate of the denominator:
\[
\frac{z_1}{z_2} = \frac{a + bi}{c + di} \cdot \frac{c - di}{c - di} = \frac{(a + bi)(c - di)}{c^2 + d^2}
\]
- Step 3: Simplify the expression:
\[
\frac{(a + bi)(c - di)}{c^2 + d^2} = \frac{ac - adi + bci - bdi^2}{c^2 + d^2} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2}
\]
- Example: \(\frac{3 + 4i}{1 + 2i} = \frac{(3 + 4i)(1 - 2i)}{1^2 + 2^2} = \frac{(3 + 4i)(1 - 2i)}{1 + 4} = \frac{3 - 6i + 4i - 8i^2}{5} = \frac{3 - 6i + 4i + 8}{5} = \frac{11 - 2i}{5} = 2.2 - 0.4i\).
- Conjugation:
The conjugate of a complex number \(z = a + bi\) is obtained by changing the sign of the imaginary part. The conjugate is denoted as \(\overline{z}\):
\[
\overline{z} = a - bi
\]
Example: The conjugate of \(3 + 4i\) is \(3 - 4i\). - Modulus:
The modulus (or absolute value) of a complex number \(z = a + bi\) is the distance from the origin to the point \((a, b)\) in the complex plane, and is given by:
\[
|z| = \sqrt{a^2 + b^2}
\]
Example: The modulus of \(3 + 4i\) is \(|3 + 4i| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\).
These operations form the foundation for working with complex numbers, enabling a wide range of applications in mathematics, physics, engineering, and other fields.
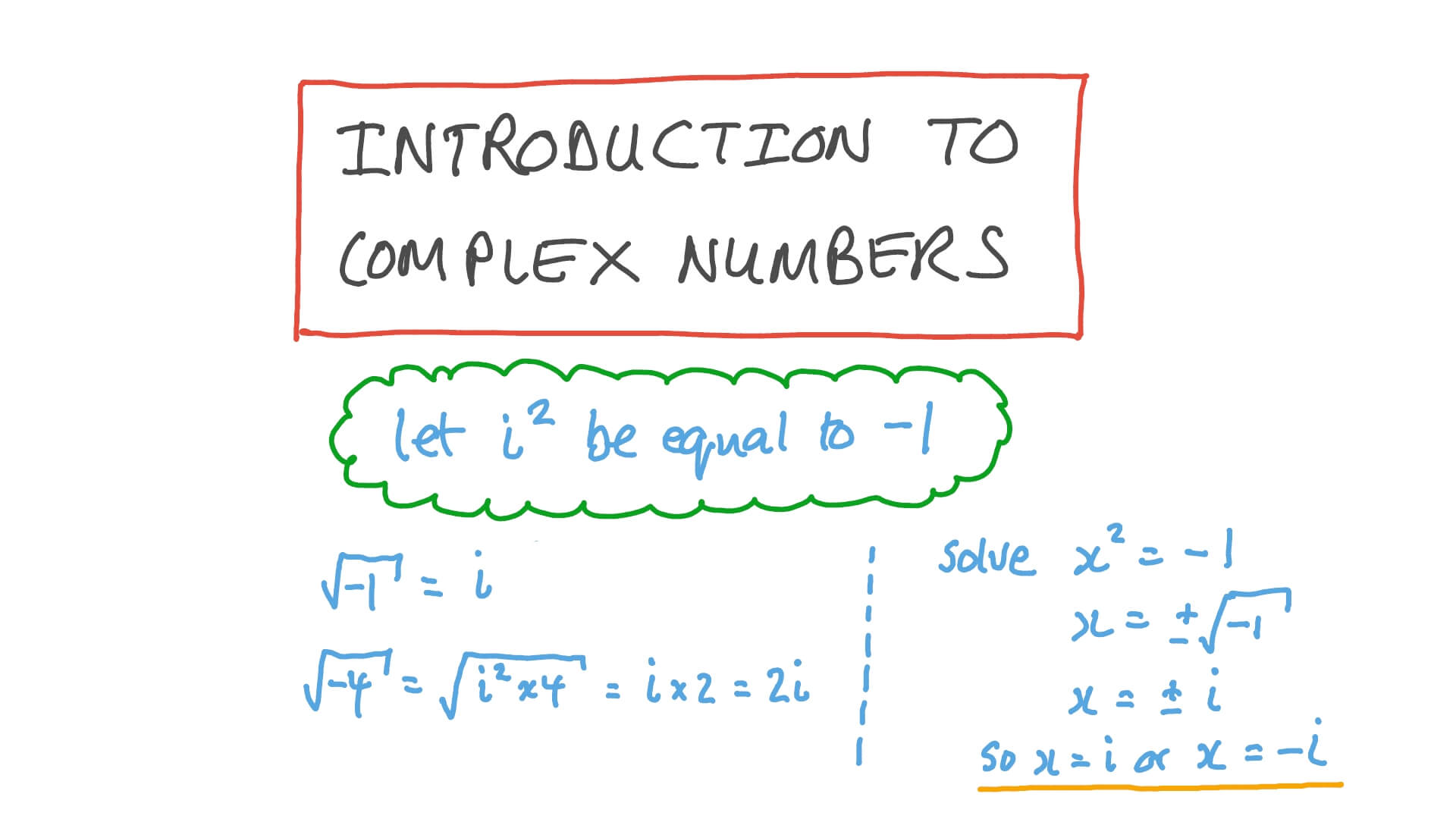
Addition and Subtraction of Complex Numbers
Complex numbers are numbers that have both a real part and an imaginary part. They are usually written in the form a + bi, where a and b are real numbers, and i is the imaginary unit defined by i2 = -1.
To add or subtract complex numbers, you simply add or subtract their real parts and their imaginary parts separately. Here’s a step-by-step guide:
Addition of Complex Numbers
Consider two complex numbers: z1 = a + bi and z2 = c + di. The sum of z1 and z2 is calculated as follows:
- Add the real parts: a + c
- Add the imaginary parts: b + d
Thus, the result is: z1 + z2 = (a + c) + (b + d)i.
Example:
Let z1 = 3 + 4i and z2 = 1 + 2i. Then:
z1 + z2 = (3 + 1) + (4 + 2)i = 4 + 6i.
Subtraction of Complex Numbers
Now, let’s consider the subtraction of the same two complex numbers, z1 and z2:
- Subtract the real parts: a - c
- Subtract the imaginary parts: b - d
Thus, the result is: z1 - z2 = (a - c) + (b - d)i.
Example:
Using the same complex numbers, z1 = 3 + 4i and z2 = 1 + 2i, we get:
z1 - z2 = (3 - 1) + (4 - 2)i = 2 + 2i.
By understanding these basic operations with complex numbers, you can handle more advanced mathematical problems involving complex numbers, such as solving quadratic equations with complex solutions or performing Fourier transforms in signal processing.
Multiplication and Division of Complex Numbers
Multiplying and dividing complex numbers is a fundamental skill in working with these numbers. Here’s a step-by-step guide to help you understand these operations:
Multiplication of Complex Numbers
To multiply two complex numbers, we use the distributive property (also known as the FOIL method for binomials). Let's consider two complex numbers \( z_1 = a + bi \) and \( z_2 = c + di \). The product \( z_1 \cdot z_2 \) is calculated as follows:
- Multiply the real parts: \( ac \)
- Multiply the outer parts: \( adi \)
- Multiply the inner parts: \( bci \)
- Multiply the imaginary parts: \( bdi^2 \)
Combine these results, remembering that \( i^2 = -1 \):
\[
z_1 \cdot z_2 = (a + bi)(c + di) = ac + adi + bci + bdi^2
\]
Since \( i^2 = -1 \), the equation simplifies to:
\[
z_1 \cdot z_2 = (ac - bd) + (ad + bc)i
\]
Example
Let's multiply \( z_1 = 3 + 4i \) and \( z_2 = 1 + 2i \):
\[
(3 + 4i)(1 + 2i) = 3 \cdot 1 + 3 \cdot 2i + 4i \cdot 1 + 4i \cdot 2i = 3 + 6i + 4i + 8i^2
\]
Since \( i^2 = -1 \), we have:
\[
3 + 6i + 4i + 8(-1) = 3 + 10i - 8 = -5 + 10i
\]
So, \( (3 + 4i)(1 + 2i) = -5 + 10i \).
Division of Complex Numbers
To divide two complex numbers, \( z_1 = a + bi \) and \( z_2 = c + di \), we multiply the numerator and the denominator by the conjugate of the denominator. The conjugate of \( z_2 \) is \( \overline{z_2} = c - di \). The process is as follows:
- Form the fraction: \( \frac{z_1}{z_2} = \frac{a + bi}{c + di} \)
- Multiply the numerator and denominator by \( \overline{z_2} \):
\[
\frac{a + bi}{c + di} \cdot \frac{c - di}{c - di} = \frac{(a + bi)(c - di)}{(c + di)(c - di)}
\]
The denominator becomes a real number because \( (c + di)(c - di) = c^2 + d^2 \). Thus, we get:
\[
\frac{(a + bi)(c - di)}{c^2 + d^2}
\]
Expanding the numerator using the distributive property:
\[
(a + bi)(c - di) = ac - adi + bci - bdi^2 = ac - adi + bci + bd
\]
Since \( i^2 = -1 \), we have:
\[
(ac + bd) + (bc - ad)i
\]
So the final result is:
\[
\frac{(ac + bd) + (bc - ad)i}{c^2 + d^2}
\]
Example
Let's divide \( z_1 = 3 + 4i \) by \( z_2 = 1 + 2i \):
\[
\frac{3 + 4i}{1 + 2i} \cdot \frac{1 - 2i}{1 - 2i} = \frac{(3 + 4i)(1 - 2i)}{(1 + 2i)(1 - 2i)}
\]
The denominator simplifies to:
\[
1 + 4 = 5
\]
Expanding the numerator:
\[
(3 + 4i)(1 - 2i) = 3 - 6i + 4i - 8i^2 = 3 - 6i + 4i + 8 = 11 - 2i
\]
So the final result is:
\[
\frac{11 - 2i}{5} = \frac{11}{5} - \frac{2}{5}i = 2.2 - 0.4i
\]
Polar Form and Exponential Form of Complex Numbers
Complex numbers can be represented in various forms, including rectangular (Cartesian), polar, and exponential forms. Here, we will explore the polar and exponential forms of complex numbers.
Polar Form of Complex Numbers
A complex number \( z = a + bi \) can be represented in polar form using the magnitude (r) and the argument (θ) of the complex number. The polar form is given by:
\( z = r(\cos \theta + i \sin \theta) \)
Where:
- \( r = \sqrt{a^2 + b^2} \) (magnitude of z)
- \( \theta = \tan^{-1}(\frac{b}{a}) \) (argument of z)
Steps to Convert to Polar Form
- Calculate the magnitude \( r \): \[ r = \sqrt{a^2 + b^2} \]
- Determine the argument \( \theta \): \[ \theta = \tan^{-1}(\frac{b}{a}) \]
- Write the complex number in polar form: \[ z = r(\cos \theta + i \sin \theta) \]
Exponential Form of Complex Numbers
The polar form can be converted to the exponential form using Euler's formula, which states:
\( e^{i \theta} = \cos \theta + i \sin \theta \)
Thus, the exponential form of a complex number is given by:
\( z = re^{i \theta} \)
Steps to Convert to Exponential Form
- Use the polar form of the complex number: \[ z = r(\cos \theta + i \sin \theta) \]
- Apply Euler's formula to get the exponential form: \[ z = re^{i \theta} \]
Examples
Let's consider a complex number \( z = 3 + 4i \):
- Calculate the magnitude: \[ r = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 \]
- Determine the argument: \[ \theta = \tan^{-1}(\frac{4}{3}) \]
- Write in polar form: \[ z = 5(\cos \theta + i \sin \theta) \]
- Convert to exponential form: \[ z = 5e^{i \theta} \]
Understanding these forms of complex numbers allows for easier multiplication, division, and other operations in the complex plane.
The Role of i in Quadratic Equations
The imaginary unit \(i\) plays a crucial role in solving quadratic equations, especially when the discriminant (the part of the quadratic formula under the square root) is negative. In such cases, the solutions involve complex numbers.
Consider a quadratic equation of the form:
\(ax^2 + bx + c = 0\)
The quadratic formula for solving this equation is given by:
\(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)
When the discriminant \(b^2 - 4ac\) is negative, the equation has no real solutions. Instead, the solutions are complex and involve the imaginary unit \(i\), where \(i^2 = -1\). Let's see how this works with an example.
Example:
Consider the quadratic equation:
\(x^2 + 1 = 0\)
Rewriting it in standard form, we get:
\(x^2 + 0x + 1 = 0\)
Here, \(a = 1\), \(b = 0\), and \(c = 1\). The discriminant is:
\(b^2 - 4ac = 0^2 - 4(1)(1) = -4\)
Since the discriminant is negative, the solutions are complex. Using the quadratic formula:
\(x = \frac{-0 \pm \sqrt{0^2 - 4 \cdot 1 \cdot 1}}{2 \cdot 1}\)
\(x = \frac{\pm \sqrt{-4}}{2}\)
\(x = \frac{\pm 2i}{2}\)
\(x = \pm i\)
Thus, the solutions to the equation \(x^2 + 1 = 0\) are \(x = i\) and \(x = -i\).
Let's consider another example with a more complex quadratic equation:
\(2x^2 + 4x + 5 = 0\)
Here, \(a = 2\), \(b = 4\), and \(c = 5\). The discriminant is:
\(b^2 - 4ac = 4^2 - 4(2)(5) = 16 - 40 = -24\)
Again, the discriminant is negative, indicating complex solutions. Using the quadratic formula:
\(x = \frac{-4 \pm \sqrt{16 - 40}}{2 \cdot 2}\)
\(x = \frac{-4 \pm \sqrt{-24}}{4}\)
\(x = \frac{-4 \pm 2i\sqrt{6}}{4}\)
\(x = \frac{-4}{4} \pm \frac{2i\sqrt{6}}{4}\)
\(x = -1 \pm \frac{i\sqrt{6}}{2}\)
Therefore, the solutions to the equation \(2x^2 + 4x + 5 = 0\) are \(x = -1 + \frac{i\sqrt{6}}{2}\) and \(x = -1 - \frac{i\sqrt{6}}{2}\).
These examples illustrate how the imaginary unit \(i\) allows us to solve quadratic equations with negative discriminants, leading to complex solutions.
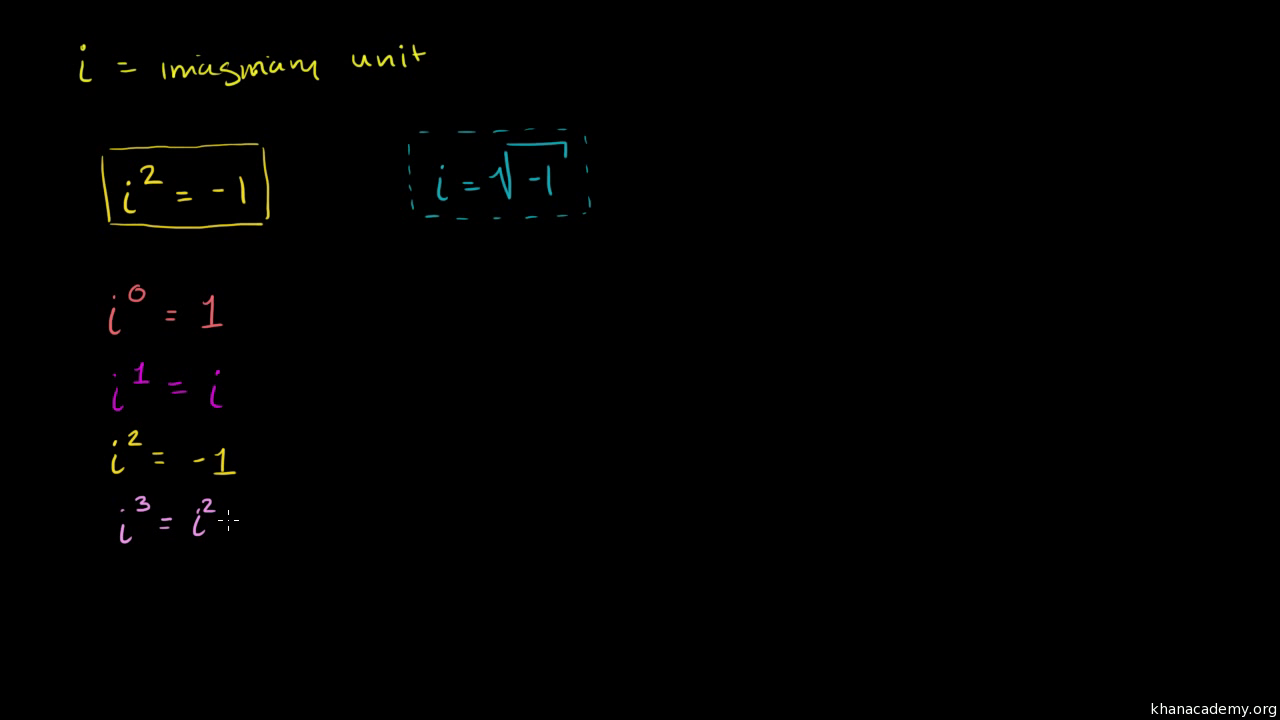
Engineering Applications of Complex Numbers
Complex numbers play a significant role in various engineering fields due to their ability to simplify calculations and provide a clear representation of physical phenomena. Here, we explore some of the key applications of complex numbers in engineering.
Control Theory
In control theory, systems are often analyzed in the frequency domain using Laplace transforms. Complex numbers are used to locate the poles and zeros of a system in the complex plane, providing insights into system stability and behavior.
Signal Analysis
Complex numbers are extensively used in signal processing. For example, they help in representing sinusoidal signals, where a complex number’s magnitude represents the amplitude and its angle represents the phase of the signal.
Electrical Engineering
In electrical engineering, alternating current (AC) circuit analysis is simplified using complex numbers. Voltages and currents are represented as phasors (complex numbers), which help in calculating impedance and analyzing circuit behavior.
- Impedance: The impedance in an AC circuit is a complex number combining resistance and reactance.
- Phasors: AC voltages and currents are represented as phasors, facilitating the use of complex algebra in circuit analysis.
Mechanical and Civil Engineering
Complex numbers are used in the design and analysis of mechanical systems involving rotations and vibrations. They simplify the mathematical modeling of oscillatory systems and help in the design of stable structures.
Quantum Mechanics
In quantum mechanics, complex numbers are fundamental. The state of a quantum system is represented by a complex wave function, and the evolution of this state is described by the Schrödinger equation, which inherently involves complex numbers.
Fluid Mechanics
Complex numbers are applied in fluid mechanics to describe potential flow in two dimensions. This application is crucial for analyzing aerodynamic properties and predicting fluid behavior around objects.
Conclusion
Complex numbers provide powerful tools for simplifying and solving a wide range of engineering problems. Their applications extend from theoretical analyses to practical implementations in various branches of engineering, making them indispensable in the field.
Complex Numbers in Electrical Engineering
Complex numbers play a crucial role in electrical engineering, particularly in the analysis of AC circuits. They provide a powerful way to represent and calculate electrical quantities such as voltage, current, and impedance.
In AC circuits, voltage and current are sinusoidal and can be described using complex numbers. A complex number has a real part and an imaginary part, often represented in the form a + bi where i is the imaginary unit with \( i^2 = -1 \). This representation is useful for capturing both the magnitude and phase of sinusoidal waveforms.
Representation of AC Quantities
AC voltages and currents can be represented in different forms:
- Rectangular Form: \( Z = a + bi \), where a is the real part and bi is the imaginary part.
- Polar Form: \( Z = A \angle \theta \), where A is the magnitude and \( \theta \) is the phase angle.
- Exponential Form: \( Z = A e^{j\theta} \), using Euler's formula \( e^{j\theta} = \cos\theta + j\sin\theta \).
These forms are interconvertible and provide flexibility in analysis and calculations. For example, converting from polar to rectangular form involves using the relationships \( a = A \cos\theta \) and \( b = A \sin\theta \).
Phasor Representation
Phasors are a specific application of complex numbers in electrical engineering. A phasor is a complex number representing the amplitude and phase of a sinusoidal function at a given frequency. This simplifies the analysis of AC circuits by transforming differential equations into algebraic equations.
For instance, the voltage and current in a resistor-inductor (RL) circuit can be represented as phasors:
- Voltage: \( V = V_m \angle \theta_V \)
- Current: \( I = I_m \angle \theta_I \)
Impedance (Z) is also a complex quantity, defined as \( Z = R + jX \), where R is the resistance and X is the reactance.
Calculations Using Complex Numbers
Complex numbers facilitate various calculations in AC circuit analysis:
- Impedance Calculation: For an inductor, \( Z_L = j\omega L \); for a capacitor, \( Z_C = \frac{1}{j\omega C} \).
- Voltage and Current Calculations: Using Ohm's Law, \( V = IZ \).
- Power Calculations: Complex power \( S = VI^* \) (where \( I^* \) is the complex conjugate of the current).
Example Calculation
Consider a series RC circuit with a resistor \( R \) and capacitor \( C \). The total impedance is:
\[
Z = R + \frac{1}{j\omega C}
\]
Using a sinusoidal source \( V = V_m \angle 0^\circ \), the current \( I \) can be calculated as:
\[
I = \frac{V}{Z} = \frac{V_m \angle 0^\circ}{R + \frac{1}{j\omega C}} = \frac{V_m}{R + \frac{1}{j\omega C}} \angle -\theta
\]
Conclusion
Understanding and utilizing complex numbers in electrical engineering is essential for analyzing and designing AC circuits. They simplify the representation and calculation of electrical quantities, making it easier to understand and solve complex problems in the field.
Complex Numbers in Signal Processing
Complex numbers play a significant role in signal processing, particularly in the analysis and manipulation of signals. They are used to represent and process signals in both time and frequency domains. Here is a detailed explanation of how complex numbers are utilized in signal processing:
1. Representation of Signals
In signal processing, complex numbers are often used to represent sinusoidal signals. A complex number can be expressed as \( z = x + yi \), where \( x \) is the real part and \( y \) is the imaginary part. This allows the representation of both amplitude and phase of a signal simultaneously.
2. Fourier Transform
The Fourier Transform is a mathematical technique used to transform a time-domain signal into its frequency-domain representation. The use of complex numbers in the Fourier Transform allows for the separation of a signal into its constituent frequencies, making it easier to analyze and manipulate.
\( F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} dt \)
Here, \( f(t) \) is the time-domain signal, \( F(\omega) \) is the frequency-domain representation, and \( \omega \) represents angular frequency.
3. In-Phase and Quadrature (IQ) Data
In radar and communication systems, signals are often represented as IQ data. This involves using complex numbers to separate the in-phase (I) and quadrature (Q) components of a signal. IQ data helps in accurate phase and amplitude measurements, which are crucial for signal demodulation and decoding.
4. Filtering and Modulation
Complex numbers are essential in the design of digital filters and modulation schemes. For instance, in Quadrature Amplitude Modulation (QAM), data is encoded into the amplitude and phase of a carrier wave using complex numbers, which increases the efficiency of data transmission.
5. Phase and Frequency Analysis
By using complex numbers, it is possible to perform precise phase and frequency analysis of signals. This is particularly useful in applications like pulse-Doppler radar, where the phase information is used to determine the velocity of moving targets.
Example of Signal Representation
Consider a signal represented as \( s(t) = A \cos(\omega t + \phi) \). This can be converted to its complex form using Euler's formula:
\( s(t) = A \cos(\omega t + \phi) = \frac{A}{2} (e^{i(\omega t + \phi)} + e^{-i(\omega t + \phi)}) \)
This complex representation simplifies many signal processing operations.
In summary, the use of complex numbers in signal processing provides a powerful framework for analyzing and manipulating signals. Their ability to represent both magnitude and phase information makes them indispensable in many advanced signal processing techniques.
Use of Imaginary Numbers in Quantum Physics
Imaginary numbers, particularly the imaginary unit \(i\), play a crucial role in quantum physics. They are integral to the mathematical framework that describes quantum systems and their behaviors.
One of the primary ways imaginary numbers appear in quantum mechanics is through the wave function, denoted as \( \psi \). The wave function describes the probability amplitude of a particle's position, momentum, and other physical properties. The time evolution of the wave function is governed by the Schrödinger equation, which prominently features the imaginary unit \(i\).
The Schrödinger equation is written as:
\[ i \hbar \frac{\partial \psi}{\partial t} = \hat{H} \psi \]
where:
- \( \hbar \) is the reduced Planck's constant,
- \( \frac{\partial \psi}{\partial t} \) is the partial derivative of the wave function with respect to time,
- \( \hat{H} \) is the Hamiltonian operator, which represents the total energy of the system.
The presence of \(i\) in the Schrödinger equation indicates the oscillatory nature of the wave function, which is essential for describing phenomena such as interference and superposition in quantum mechanics. These properties are fundamental to the behavior of quantum systems and cannot be accurately described without the use of complex numbers.
Imaginary numbers also appear in the formulation of other quantum mechanical principles, such as Heisenberg's uncertainty principle and the representation of spin states. For example, the eigenvalues of certain operators, such as the angular momentum operator, can involve complex numbers, reflecting the intrinsic quantum mechanical property of spin.
In addition to theoretical applications, imaginary numbers are used in practical computations within quantum mechanics. For instance, they are employed in the calculation of probabilities and expectation values, which are essential for predicting the outcomes of quantum experiments.
Moreover, the role of \(i\) is not merely a mathematical convenience; it has physical implications. Research has shown that complex numbers are necessary for accurately describing the outcomes of certain quantum experiments, such as the Bell test, which demonstrates the non-locality and entanglement of quantum particles. These experiments suggest that the complex formulation of quantum mechanics is not just a mathematical artifact but a reflection of the underlying physical reality.
In conclusion, imaginary numbers, through the use of \(i\), are indispensable in quantum physics. They provide the mathematical structure needed to describe and predict the behavior of quantum systems, highlighting the deep connection between mathematics and the physical world.

Advanced Mathematical Theories Involving i
Imaginary and complex numbers play crucial roles in various advanced mathematical theories and applications. Some of the key theories and concepts involving the imaginary unit \(i\) are:
Euler's Formula and Identity
Euler's formula is a fundamental equation in complex analysis, given by:
\(e^{ix} = \cos(x) + i\sin(x)\)
When \(x = \pi\), this formula simplifies to Euler's identity, one of the most beautiful equations in mathematics:
\(e^{i\pi} + 1 = 0\)
This identity links five of the most important numbers in mathematics: \(e\), \(i\), \(\pi\), 1, and 0.
Complex Exponentiation and Roots
Complex exponentiation extends the idea of powers and roots to the complex plane. For any complex number \(z = re^{i\theta}\), where \(r\) is the magnitude and \(\theta\) is the argument:
\(z^n = r^n e^{in\theta}\)
Similarly, finding the \(n\)-th root of a complex number involves:
\(z^{1/n} = r^{1/n} e^{i(\theta + 2k\pi)/n}\) for \(k = 0, 1, ..., n-1\)
This reveals that complex numbers have \(n\) distinct roots, evenly spaced around the origin in the complex plane.
Analytic Continuation and Riemann Zeta Function
The concept of analytic continuation is used to extend the domain of complex functions. The Riemann zeta function, defined initially for complex numbers with real part greater than 1, can be analytically continued to other complex numbers:
\(\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s}\)
This function plays a critical role in number theory, particularly in the distribution of prime numbers, as encapsulated by the Riemann Hypothesis.
Complex Dynamics and Fractals
Complex numbers are essential in the study of dynamical systems and fractals. The Mandelbrot set is a famous example, defined by iterating the function:
\(f_c(z) = z^2 + c\)
where \(z\) and \(c\) are complex numbers. The boundary of the Mandelbrot set displays intricate, self-similar patterns at every scale, demonstrating the beauty of complex dynamics.
Quantum Mechanics and Wave Functions
In quantum mechanics, complex numbers are used to describe wave functions, which encapsulate the probabilities of finding particles in various states. The Schrödinger equation, a fundamental equation in quantum mechanics, involves complex wave functions:
\(i\hbar \frac{\partial \psi}{\partial t} = \hat{H} \psi\)
where \(\psi\) is the wave function, \(\hbar\) is the reduced Planck constant, and \(\hat{H}\) is the Hamiltonian operator.
These advanced mathematical theories highlight the profound importance and utility of imaginary numbers, particularly the imaginary unit \(i\), in various fields of mathematics and physics.
Euler's Formula and its Implications
Euler's formula, a cornerstone in complex analysis, is expressed as:
\[ e^{ix} = \cos{x} + i \sin{x} \]
where \( e \) is Euler's number, \( i \) is the imaginary unit, and \( x \) is a real number. This elegant formula establishes a profound relationship between the exponential function and trigonometric functions.
Derivation of Euler's Formula
The derivation of Euler's formula begins with the Taylor series expansion for the exponential function \( e^x \):
\[ e^{x} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \ldots \]
Substituting \( ix \) for \( x \) in the series gives:
\[ e^{ix} = 1 + ix + \frac{(ix)^2}{2!} + \frac{(ix)^3}{3!} + \frac{(ix)^4}{4!} + \ldots \]
Recognizing that \( i^2 = -1 \), \( i^3 = -i \), and \( i^4 = 1 \), this can be separated into real and imaginary parts:
\[ e^{ix} = \left(1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \ldots \right) + i \left(x - \frac{x^3}{3!} + \frac{x^5}{5!} - \ldots \right) \]
These series are the Maclaurin series for \( \cos{x} \) and \( \sin{x} \), respectively:
\[ e^{ix} = \cos{x} + i \sin{x} \]
Implications and Applications
Euler's formula has several profound implications:
- Complex Plane Representation: Any complex number \( z \) can be represented in polar form as \( re^{i\theta} \), where \( r \) is the magnitude and \( \theta \) is the argument (angle).
- Euler's Identity: When \( x = \pi \), Euler's formula simplifies to the celebrated identity:
\[ e^{i\pi} + 1 = 0 \]
This equation elegantly links five fundamental mathematical constants: 0, 1, \( \pi \), \( e \), and \( i \). - Trigonometric Identities: Euler's formula allows for easy derivation of trigonometric identities. For example:
\[ \cos{x} = \frac{e^{ix} + e^{-ix}}{2} \]
\[ \sin{x} = \frac{e^{ix} - e^{-ix}}{2i} \]
- Rotations in the Complex Plane: Multiplication by \( e^{i\theta} \) corresponds to a counterclockwise rotation by \( \theta \) radians in the complex plane.
Geometric Interpretation
Euler's formula is key to understanding the geometric interpretation of complex numbers. On the complex plane, \( e^{ix} \) represents a point on the unit circle at an angle \( x \) from the positive real axis.
For example, the complex number \( e^{i\pi/2} \) is located at \( (0, 1) \) on the complex plane, corresponding to a 90-degree rotation counterclockwise.
Conclusion
Euler's formula is a fundamental result in mathematics that bridges the exponential function, complex numbers, and trigonometry. Its applications span numerous fields including engineering, physics, and signal processing, making it an essential tool in both theoretical and applied mathematics.
Hướng dẫn chi tiết cách sử dụng số phức i bình phương trong toán học, giúp bạn hiểu rõ hơn về khái niệm và ứng dụng của i bình phương.
Cách Sử Dụng i Bình Phương
READ MORE:
Video này hướng dẫn cách thay thế i bình phương trong các phép toán phức tạp, giúp bạn hiểu rõ hơn về khái niệm và ứng dụng của i bình phương trong toán học.
Thay Thế i Bình Phương




x-1=sec(squared)x.jpg)








