Topic x squared minus x: "X squared minus x" is a fundamental quadratic expression that plays a significant role in algebra. This article delves into the techniques for solving quadratic equations, including factoring, using the quadratic formula, and graphing. Understand the applications and real-world examples of this important mathematical concept to enhance your algebra skills.
Table of Content
- x Squared Minus x
- Introduction to Quadratic Expressions
- Basic Algebraic Operations
- Factoring Techniques
- Graphing Quadratic Functions
- Applications of Quadratic Equations
- Practice Problems and Solutions
- Step-by-Step Solving Methods
- Completing the Square
- Quadratic Formula
- Difference of Squares
- Real-World Examples and Word Problems
- Additional Resources and Tools
- YOUTUBE: Giải phương trình x bình phương = 4 và tìm hiểu các giá trị bình phương khác của x. Video này sẽ giúp bạn nắm vững cách giải các bài toán liên quan đến bình phương của x.
x Squared Minus x
The expression \(x^2 - x\) is a quadratic polynomial. Quadratic polynomials are fundamental in algebra and have various applications in mathematics and related fields.
General Form
A quadratic polynomial is of the form \(ax^2 + bx + c\). In the case of \(x^2 - x\), the coefficients are \(a = 1\), \(b = -1\), and \(c = 0\).
Factoring the Expression
The expression \(x^2 - x\) can be factored by taking out the common factor:
\[
x^2 - x = x(x - 1)
\]
Solving Quadratic Equations
To solve the quadratic equation \(x^2 - x = 0\), we set the expression equal to zero and solve for \(x\):
\[
x(x - 1) = 0
\]
Setting each factor to zero gives the solutions:
\[
x = 0 \quad \text{or} \quad x = 1
\]
Graphical Representation
The graph of \(y = x^2 - x\) is a parabola that opens upwards. The roots of the equation \(x^2 - x = 0\) are the points where the graph intersects the x-axis, which are \(x = 0\) and \(x = 1\).
Applications
Quadratic polynomials like \(x^2 - x\) are used in various fields such as physics, engineering, and economics to model parabolic relationships. They are also essential in solving optimization problems and in the study of quadratic functions.
Examples
- Example 1: Solve \(x^2 - x = 0\).
- Solution: The roots are \(x = 0\) and \(x = 1\).
- Example 2: Factorize \(x^2 - x\).
- Solution: \(x(x - 1)\).
Additional Resources
For further exploration of quadratic equations and their solutions, you can use online tools like the on Mathway or the on Math is Fun.

READ MORE:
Introduction to Quadratic Expressions
A quadratic expression is a polynomial of degree 2, typically in the form \( ax^2 + bx + c \). Quadratic expressions are fundamental in algebra and have applications across various fields such as physics, engineering, and economics. The term "quadratic" comes from "quad" meaning square, since the variable is squared (\( x^2 \)).
Quadratic expressions can be factored, solved, and graphically represented in various ways. Understanding these methods is crucial for solving quadratic equations and interpreting their solutions. Let's delve into the key concepts and methods related to quadratic expressions.
Factoring Quadratic Expressions
Factoring is one of the primary methods to simplify quadratic expressions. For example, to factor \( x^2 - x \), we look for two numbers that multiply to the constant term and add to the coefficient of the linear term. Here’s how you can factor \( x^2 - x \):
- Rewrite the expression: \( x(x - 1) \)
- Check your work by expanding the factors: \( x(x - 1) = x^2 - x \)
Solving Quadratic Equations
To solve a quadratic equation like \( x^2 - x = 0 \), set the expression to zero and solve for \( x \). This can be done by factoring, using the quadratic formula, or completing the square. For \( x^2 - x = 0 \):
- Factor the equation: \( x(x - 1) = 0 \)
- Set each factor to zero: \( x = 0 \) or \( x - 1 = 0 \)
- Thus, the solutions are \( x = 0 \) and \( x = 1 \)
Graphing Quadratic Functions
Graphing is a visual way to represent quadratic functions. The graph of a quadratic function is a parabola. For \( y = x^2 - x \):
- The vertex of the parabola can be found by using the formula \( x = -\frac{b}{2a} \)
- The axis of symmetry is the line that passes through the vertex
- The direction of the parabola (upward or downward) is determined by the sign of \( a \)
Applications of Quadratic Expressions
Quadratic expressions appear in various real-world scenarios. They are used to model projectile motion, determine the maximum area of a given perimeter, and in financial calculations such as profit maximization.
By mastering quadratic expressions, you can solve complex problems and gain deeper insights into mathematical relationships and patterns.
Basic Algebraic Operations
Algebraic operations are fundamental tools for solving mathematical problems. Understanding these operations allows for the manipulation and simplification of expressions and equations. Here are some key basic algebraic operations:
- Addition and Subtraction: Combine like terms by adding or subtracting their coefficients. For example, \(2x + 3x = 5x\) and \(5x - 2x = 3x\).
- Multiplication: Use the distributive property to multiply terms. For instance, \(2x \cdot 3x = 6x^2\).
- Division: Simplify expressions by dividing coefficients and reducing powers. For example, \(\frac{6x^2}{3x} = 2x\).
- Exponentiation: Apply rules for exponents such as \(a^m \cdot a^n = a^{m+n}\). For example, \(x^2 \cdot x^3 = x^5\).
- Factoring: Break down complex expressions into products of simpler factors. For instance, \(x^2 - 5x + 6 = (x - 2)(x - 3)\).
- Solving Equations: Isolate the variable on one side to find its value. For example, \(2x + 4 = 10\) simplifies to \(x = 3\).
Mastering these basic operations is crucial for more advanced mathematical concepts and problem-solving.
Factoring Techniques
Factoring is a fundamental algebraic technique used to simplify expressions and solve equations. Here, we will explore various methods to factor expressions effectively, especially focusing on quadratic expressions like \(x^2 - x\).
-
Common Factor
The first step in factoring is to look for a common factor in all terms of the expression. For example, in the expression \(x^2 - x\), the common factor is \(x\). Therefore, \(x^2 - x\) can be factored as:
\[
x^2 - x = x(x - 1)
\] -
Difference of Squares
The difference of squares is a specific type of factoring used when an expression is in the form \(a^2 - b^2\). This can be factored into \((a + b)(a - b)\). For example:
\[
x^2 - 1 = (x + 1)(x - 1)
\] -
Trinomials
To factor trinomials of the form \(ax^2 + bx + c\), we look for two numbers that multiply to \(ac\) and add to \(b\). For instance, to factor \(x^2 - x - 6\), we find two numbers that multiply to \(-6\) and add to \(-1\), which are \(-3\) and \(2\). Thus:
\[
x^2 - x - 6 = (x - 3)(x + 2)
\] -
Grouping
Grouping is used when an expression has four or more terms. The terms are grouped in pairs, and common factors are factored out. For example, for the expression \(x^3 + x^2 + x + 1\), group and factor as follows:
\[
x^3 + x^2 + x + 1 = x^2(x + 1) + 1(x + 1) = (x^2 + 1)(x + 1)
\] -
Quadratic Formula
When factoring is not straightforward, the quadratic formula can be used to find the roots of the quadratic equation \(ax^2 + bx + c = 0\). The roots are given by:
\[
x = \frac{{-b \pm \sqrt{b^2 - 4ac}}}{2a}
\]Once the roots are found, they can be used to factor the quadratic expression. For example, if the roots are \(r_1\) and \(r_2\), the factored form is:
\[
ax^2 + bx + c = a(x - r_1)(x - r_2)
\]
Graphing Quadratic Functions
Graphing quadratic functions is an essential skill in understanding the behavior of these functions. A quadratic function is typically of the form \( y = ax^2 + bx + c \). In this section, we will focus on the quadratic function \( y = x^2 - x \) and explore how to graph it step by step.
Steps to Graph the Function \( y = x^2 - x \)
- Identify the Coefficients:
For the quadratic function \( y = x^2 - x \), the coefficients are:
- \( a = 1 \)
- \( b = -1 \)
- \( c = 0 \)
- Find the Vertex:
The vertex of a quadratic function \( y = ax^2 + bx + c \) can be found using the formula \( x = -\frac{b}{2a} \). For \( y = x^2 - x \):
- \( x = -\frac{-1}{2 \cdot 1} = \frac{1}{2} \)
Substituting \( x = \frac{1}{2} \) into the function to find the y-coordinate:
- \( y = \left( \frac{1}{2} \right)^2 - \frac{1}{2} = \frac{1}{4} - \frac{1}{2} = -\frac{1}{4} \)
Therefore, the vertex is \( \left( \frac{1}{2}, -\frac{1}{4} \right) \).
- Determine the Axis of Symmetry:
The axis of symmetry for a quadratic function is the vertical line that passes through the vertex. For \( y = x^2 - x \), the axis of symmetry is \( x = \frac{1}{2} \).
- Find the Y-Intercept:
The y-intercept is the point where the graph intersects the y-axis. This occurs when \( x = 0 \):
- \( y = 0^2 - 0 = 0 \)
Therefore, the y-intercept is \( (0, 0) \).
- Plot Additional Points:
To get a more accurate graph, plot additional points by choosing x-values and calculating the corresponding y-values. For example:
- For \( x = 1 \), \( y = 1^2 - 1 = 0 \)
- For \( x = -1 \), \( y = (-1)^2 - (-1) = 1 + 1 = 2 \)
- For \( x = 2 \), \( y = 2^2 - 2 = 4 - 2 = 2 \)
- Draw the Parabola:
Using the vertex, axis of symmetry, y-intercept, and additional points, draw a smooth curve to represent the parabola. The parabola opens upwards because the coefficient \( a = 1 \) is positive.
Example Table of Values
| x | y |
|---|---|
| -2 | 6 |
| -1 | 2 |
| 0 | 0 |
| 0.5 | -0.25 |
| 1 | 0 |
| 2 | 2 |
By following these steps, you can accurately graph the quadratic function \( y = x^2 - x \) and understand its key features.

Applications of Quadratic Equations
Quadratic equations are used in a variety of real-world applications across different fields. Below are some common applications of quadratic equations:
1. Projectile Motion
One of the most famous applications of quadratic equations is in modeling the trajectory of projectiles. The equation for the height \( h \) of an object at any time \( t \) is given by:
\( h(t) = -\frac{1}{2}gt^2 + v_0t + h_0 \)
where:
- \( g \) is the acceleration due to gravity (9.8 m/s2 on Earth)
- \( v_0 \) is the initial velocity
- \( h_0 \) is the initial height
This equation helps predict the height of an object at any given time and is useful in sports, engineering, and various other fields.
2. Area Problems
Quadratic equations are frequently used to solve problems involving areas of geometric shapes. For example, consider a rectangle whose length is 7 cm more than its width and whose area is 78 cm2. If we let \( w \) be the width and \( l \) be the length, we can set up the following equations:
\( l = w + 7 \)
\( w(w + 7) = 78 \)
Solving this quadratic equation gives us the dimensions of the rectangle.
3. Economics and Business
In economics, quadratic equations are used to model cost, revenue, and profit functions. For instance, the total cost \( C \) of producing \( x \) units of a product might be modeled by:
\( C(x) = ax^2 + bx + c \)
where \( a \), \( b \), and \( c \) are constants. Finding the minimum cost or maximum profit often involves solving quadratic equations.
4. Optimization Problems
Quadratic equations are essential in optimization problems where one needs to find the maximum or minimum value of a certain quantity. For example, maximizing the area of a rectangular enclosure with a fixed perimeter involves solving a quadratic equation to determine the optimal dimensions.
5. Physics and Engineering
In physics and engineering, quadratic equations are used to analyze forces, motion, and energy. For example, the equation for the potential energy \( U \) stored in a spring is:
\( U = \frac{1}{2}kx^2 \)
where \( k \) is the spring constant and \( x \) is the displacement from the equilibrium position. This is a quadratic equation in \( x \).
6. Geometry
Many geometric problems involving circles, parabolas, ellipses, and hyperbolas lead to quadratic equations. For instance, finding the points of intersection between a line and a parabola requires solving a quadratic equation.
7. Real-World Scenarios
Quadratic equations can model various real-world scenarios, such as calculating the time it takes for an object to hit the ground, determining the optimal price to maximize revenue, or finding the dimensions that minimize material usage while maintaining structural integrity.
These applications illustrate the versatility and importance of quadratic equations in solving practical problems in different domains.
Practice Problems and Solutions
Here are some practice problems involving quadratic equations, along with detailed solutions. These problems will help you understand various methods of solving quadratic equations.
-
Problem 1: Solve the quadratic equation \(x^2 - x - 6 = 0\)
Solution:
- First, we factor the quadratic equation: \(x^2 - x - 6 = (x - 3)(x + 2) = 0\)
- Setting each factor to zero: \(x - 3 = 0\) or \(x + 2 = 0\)
- Solving for \(x\): \(x = 3\) or \(x = -2\)
-
Problem 2: Solve the quadratic equation using the quadratic formula: \(2x^2 - 4x - 6 = 0\)
Solution:
- Identify \(a\), \(b\), and \(c\): \(a = 2\), \(b = -4\), \(c = -6\)
- Quadratic formula: \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)
- Substitute values: \(x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(2)(-6)}}{2(2)}\)
- Simplify under the square root: \(x = \frac{4 \pm \sqrt{16 + 48}}{4} = \frac{4 \pm \sqrt{64}}{4}\)
- Simplify further: \(x = \frac{4 \pm 8}{4}\)
- Solutions: \(x = \frac{4 + 8}{4} = 3\) and \(x = \frac{4 - 8}{4} = -1\)
-
Problem 3: Solve by completing the square: \(x^2 + 6x + 5 = 0\)
Solution:
- Move the constant term to the other side: \(x^2 + 6x = -5\)
- Add \((\frac{6}{2})^2 = 9\) to both sides: \(x^2 + 6x + 9 = 4\)
- Rewrite as a square: \((x + 3)^2 = 4\)
- Solve for \(x\): \(x + 3 = \pm 2\)
- Solutions: \(x = -3 + 2 = -1\) and \(x = -3 - 2 = -5\)
-
Problem 4: Solve the quadratic equation: \(x^2 - 4 = 0\) (Difference of squares)
Solution:
- Rewrite as a difference of squares: \((x - 2)(x + 2) = 0\)
- Setting each factor to zero: \(x - 2 = 0\) or \(x + 2 = 0\)
- Solutions: \(x = 2\) or \(x = -2\)
Step-by-Step Solving Methods
Quadratic equations can be solved using various methods. Here, we'll go through three common methods step-by-step: factoring, completing the square, and using the quadratic formula.
1. Factoring Method
To solve the quadratic equation \(x^2 - x = 0\) by factoring, follow these steps:
- Rewrite the equation: \(x^2 - x = 0\).
- Factor out the common term \(x\): \(x(x - 1) = 0\).
- Set each factor to zero: \(x = 0\) and \(x - 1 = 0\).
- Solve for \(x\): \(x = 0\) and \(x = 1\).
So, the solutions are \(x = 0\) and \(x = 1\).
2. Completing the Square
To solve \(x^2 - x = 0\) by completing the square, follow these steps:
- Rewrite the equation in the form \(x^2 - x = 0\).
- Move the constant term to the right side: \(x^2 - x = 0\).
- Add and subtract \(\left(\frac{1}{2}\right)^2\) inside the equation: \(x^2 - x + \left(\frac{1}{2}\right)^2 = \left(\frac{1}{2}\right)^2\).
- Rewrite the left side as a perfect square: \(\left(x - \frac{1}{2}\right)^2 = \frac{1}{4}\).
- Take the square root of both sides: \(x - \frac{1}{2} = \pm \frac{1}{2}\).
- Solve for \(x\): \(x = \frac{1}{2} + \frac{1}{2}\) and \(x = \frac{1}{2} - \frac{1}{2}\).
- Simplify the solutions: \(x = 1\) and \(x = 0\).
So, the solutions are \(x = 0\) and \(x = 1\).
3. Quadratic Formula
The quadratic formula is used to solve any quadratic equation of the form \(ax^2 + bx + c = 0\). The formula is:
\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
For the equation \(x^2 - x = 0\):
- Identify the coefficients: \(a = 1\), \(b = -1\), and \(c = 0\).
- Plug these values into the quadratic formula:
- Simplify the equation:
- Calculate the solutions:
- Solve for \(x\):
\[x = \frac{-(-1) \pm \sqrt{(-1)^2 - 4(1)(0)}}{2(1)}\]
\[x = \frac{1 \pm \sqrt{1}}{2}\]
\[x = \frac{1 \pm 1}{2}\]
\[x = 1 \quad \text{and} \quad x = 0\]
So, the solutions are \(x = 0\) and \(x = 1\).
Summary
All three methods—factoring, completing the square, and using the quadratic formula—provide the same solutions for the quadratic equation \(x^2 - x = 0\): \(x = 0\) and \(x = 1\). Understanding these methods helps in solving a wide range of quadratic equations efficiently.
Completing the Square
Completing the square is a method used to solve quadratic equations by transforming them into a perfect square trinomial. This technique makes it easier to solve for the variable and understand the properties of the quadratic function. Follow these steps to complete the square for the quadratic equation \(x^2 - x\):
- Start with the standard form of the quadratic equation:
\[ x^2 - x + c = 0 \]
- Move the constant term to the right side of the equation:
\[ x^2 - x = -c \]
- Find the coefficient of the \(x\) term, divide it by 2, and square the result:
The coefficient of \(x\) is -1. Dividing by 2 gives \(-\frac{1}{2}\). Squaring \(-\frac{1}{2}\) gives \(\frac{1}{4}\).
\[ \left( -\frac{1}{2} \right)^2 = \frac{1}{4} \]
- Add this square to both sides of the equation to maintain balance:
\[ x^2 - x + \frac{1}{4} = -c + \frac{1}{4} \]
- Rewrite the left side of the equation as a squared binomial:
\[ \left( x - \frac{1}{2} \right)^2 = -c + \frac{1}{4} \]
- Solve for \(x\) by taking the square root of both sides:
\[ x - \frac{1}{2} = \pm \sqrt{-c + \frac{1}{4}} \]
Therefore,
\[ x = \frac{1}{2} \pm \sqrt{-c + \frac{1}{4}} \]
Let's go through an example with a specific quadratic equation:
Example: Solve \(x^2 - 4x + 4 = 0\) by completing the square
- Start with the equation:
\[ x^2 - 4x + 4 = 0 \]
- Move the constant term to the right side:
\[ x^2 - 4x = -4 \]
- Find the coefficient of the \(x\) term, divide it by 2, and square it:
The coefficient of \(x\) is -4. Dividing by 2 gives -2. Squaring -2 gives 4.
\[ \left( -2 \right)^2 = 4 \]
- Add this square to both sides:
\[ x^2 - 4x + 4 = -4 + 4 \]
\[ x^2 - 4x + 4 = 0 \]
- Rewrite the left side as a squared binomial:
\[ \left( x - 2 \right)^2 = 0 \]
- Solve for \(x\) by taking the square root of both sides:
\[ x - 2 = 0 \]
\[ x = 2 \]
Completing the square not only helps in solving quadratic equations but also in rewriting them in vertex form, which is useful for graphing and understanding the properties of the quadratic function. Practice with different equations to master this technique!

Quadratic Formula
The quadratic formula is a powerful tool used to solve quadratic equations of the form \(ax^2 + bx + c = 0\). The formula provides the solutions (or roots) for the quadratic equation:
\( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
Here, a, b, and c are coefficients of the equation, and \(a \neq 0\). The term under the square root, \(b^2 - 4ac\), is known as the discriminant.
Steps to Solve Using the Quadratic Formula
- Identify the coefficients: From the quadratic equation \(ax^2 + bx + c = 0\), determine the values of a, b, and c.
- Calculate the discriminant: Compute the value of the discriminant using \(b^2 - 4ac\).
- If the discriminant is positive, the equation has two real and distinct solutions.
- If the discriminant is zero, the equation has exactly one real solution.
- If the discriminant is negative, the equation has two complex solutions.
- Apply the quadratic formula: Substitute the values of a, b, and c into the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) to find the solutions.
Example
Let's solve the quadratic equation \(2x^2 - 4x - 6 = 0\) using the quadratic formula.
- Identify the coefficients: \(a = 2\), \(b = -4\), \(c = -6\)
- Calculate the discriminant:
\( \Delta = (-4)^2 - 4 \cdot 2 \cdot (-6) = 16 + 48 = 64 \)
Since the discriminant is positive, there are two real solutions.
- Apply the quadratic formula:
\( x = \frac{-(-4) \pm \sqrt{64}}{2 \cdot 2} = \frac{4 \pm 8}{4} \)
This gives us two solutions:
\( x = \frac{4 + 8}{4} = 3 \) and \( x = \frac{4 - 8}{4} = -1 \)
Thus, the solutions to the equation \(2x^2 - 4x - 6 = 0\) are \(x = 3\) and \(x = -1\).
Key Points
- The quadratic formula can solve any quadratic equation, whether the solutions are real or complex.
- The discriminant (\(b^2 - 4ac\)) determines the nature of the roots.
- It's a universal method, especially useful when other methods like factoring are not straightforward.
Using the quadratic formula is a systematic approach to find the roots of any quadratic equation, ensuring that all possible solutions are considered.
Difference of Squares
The difference of squares is a special case of polynomial factorization that applies when you have two squared terms separated by a subtraction sign. The general formula for factoring a difference of squares is:
\[a^2 - b^2 = (a - b)(a + b)\]
Let's apply this formula step-by-step to the expression \(x^2 - x\).
-
Identify the terms to be squared:
Rewrite \(x^2 - x\) in a form that fits the difference of squares pattern. Notice that this expression can be written as:
\[x^2 - x = x^2 - x \cdot 1\]
However, for it to match the difference of squares pattern perfectly, it must be in the form \(a^2 - b^2\). Therefore, we need to find a way to make both terms perfect squares, which isn't possible here since \(x \cdot 1\) isn't a perfect square.
-
Instead, let's consider another example: \(x^2 - 9\). This expression fits the pattern as both terms are perfect squares:
\[x^2 - 9 = x^2 - 3^2\]
-
Apply the difference of squares formula:
Using the formula \(a^2 - b^2 = (a - b)(a + b)\), let \(a = x\) and \(b = 3\):
\[x^2 - 9 = (x - 3)(x + 3)\]
-
Verify the factorization:
To ensure our factorization is correct, multiply the factors back together:
\[(x - 3)(x + 3) = x(x + 3) - 3(x + 3) = x^2 + 3x - 3x - 9 = x^2 - 9\]
Additional examples:
- Example 1: Factor \(4x^2 - 25\)
- Example 2: Factor \(9x^6 - y^8\)
Rewrite as \((2x)^2 - 5^2\)
Factor using the formula:
\[4x^2 - 25 = (2x - 5)(2x + 5)\]
Rewrite as \((3x^3)^2 - (y^4)^2\)
Factor using the formula:
\[9x^6 - y^8 = (3x^3 - y^4)(3x^3 + y^4)\]
The difference of squares technique is useful for simplifying expressions and solving equations, particularly when dealing with higher degree polynomials or complex algebraic fractions.
Real-World Examples and Word Problems
Quadratic equations frequently appear in real-world situations. Here are a few examples and word problems that illustrate their applications:
1. Projectile Motion
When an object is thrown into the air, its path can be modeled by a quadratic equation. For example, the height \(h\) of a ball thrown upwards can be given by:
\[ h(t) = -16t^2 + vt + h_0 \]
- Problem: A ball is thrown upwards with an initial velocity of 48 feet per second from a height of 5 feet. Determine the time when the ball will hit the ground.
- Solution: Set \(h(t) = 0\) and solve the quadratic equation \(-16t^2 + 48t + 5 = 0\) using the quadratic formula.
2. Area Optimization
Quadratics can be used to optimize areas, such as maximizing the area of a garden given a fixed perimeter.
- Problem: You have 60 meters of fencing to create a rectangular garden. What dimensions will maximize the area?
- Solution: Express the area \(A\) as a function of width \(w\) and solve the quadratic equation derived from \(A(w) = w(30 - w)\).
3. Economics
Quadratic equations can model profit functions in business.
- Problem: A company's profit \(P\) in thousands of dollars is given by \(P(x) = -5x^2 + 40x - 60\), where \(x\) is the number of units sold in thousands. Determine the number of units that maximizes profit.
- Solution: Find the vertex of the parabola \(P(x) = -5x^2 + 40x - 60\) to determine the maximum profit.
4. Chemistry
Quadratic equations can appear in chemical reaction rates and concentrations.
- Problem: In a chemical reaction, the concentration \(C\) of a substance after time \(t\) minutes is given by \(C(t) = 2t^2 - 4t + 1\). Find the time at which the concentration is at a minimum.
- Solution: Find the vertex of the parabola \(C(t) = 2t^2 - 4t + 1\).
5. Geometry
Quadratic equations can solve problems involving geometric shapes.
- Problem: The length of a rectangle is 3 meters longer than its width. If the area of the rectangle is 70 square meters, find its dimensions.
- Solution: Let the width be \(x\) meters. Then, the length is \(x + 3\) meters. Set up the equation \(x(x + 3) = 70\) and solve for \(x\).
These examples demonstrate the versatility of quadratic equations in modeling and solving real-world problems.
Additional Resources and Tools
To further enhance your understanding and application of quadratic equations, here are some useful resources and tools:
-
Desmos Graphing Calculator
This powerful online tool allows you to graph and analyze quadratic functions with ease. You can visualize the behavior of the function \(x^2 - x\), find the vertex, and see the impact of changes in the coefficients.
-
Mathway Quadratic Formula Calculator
Enter your quadratic equation to get solutions using the quadratic formula. This tool also provides step-by-step solutions to help you understand the process.
-
Symbolab Quadratic Equation Solver
Symbolab offers an intuitive interface to solve quadratic equations, showing detailed steps for methods such as factoring, completing the square, and using the quadratic formula.
-
Math is Fun Quadratic Equation Solver
This educational website provides a user-friendly quadratic equation solver along with explanations of the concepts and formulas involved. It’s a great resource for learning and practice.
Using these resources, you can gain a deeper understanding of quadratic equations, practice solving them, and visualize their graphs to see how they behave in different scenarios.

Giải phương trình x bình phương = 4 và tìm hiểu các giá trị bình phương khác của x. Video này sẽ giúp bạn nắm vững cách giải các bài toán liên quan đến bình phương của x.
Giải x bình phương = 4 và các giá trị bình phương khác của x
READ MORE:
Hướng dẫn chi tiết cách giải phương trình x^2 - x + 2 = 0 bằng phương pháp nhân tử. Video này giúp bạn hiểu rõ hơn về cách phân tích các phương trình bậc hai.
Cách Giải x^2 - x + 2 = 0 bằng Phương Pháp Nhân Tử



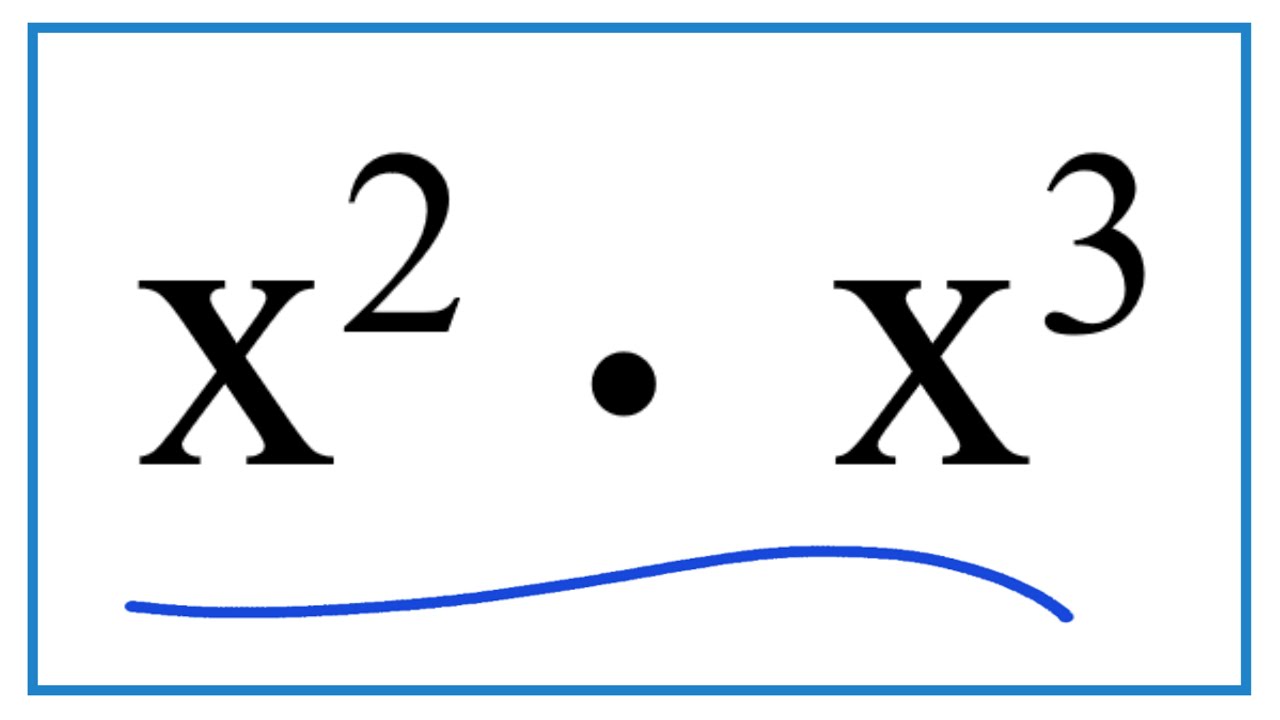



x-1=sec(squared)x.jpg)





