Topic 3x times x squared: Discover the simplicity and elegance of the expression 3x times x squared. In this article, we will explore how to simplify 3x times x squared, turning it into a more manageable form. Join us as we delve into the basics of algebra and unravel the steps to master this fundamental concept.
Table of Content
- Understanding the Expression \(3x \times x^2\)
- Understanding Basic Algebraic Expressions
- Introduction to Polynomials
- Simplification Techniques
- Solving Algebraic Equations
- Using Online Calculators
- Graphical Representation of Equations
- Complex Numbers and Operations
- Matrix Calculations
- Calculus and its Applications
- Statistics in Algebra
- Step-by-Step Algebra Examples
- Additional Mathematical Concepts
- Mathematical Problem Solving Techniques
- Applications in Real-World Scenarios
- Interactive Learning Tools
- Advanced Algebra Topics
- Resources and References
- YOUTUBE: Video hướng dẫn cách bình phương biểu thức: (3x)^2 và (3+x)^2, chi tiết và dễ hiểu cho người học toán.
Understanding the Expression \(3x \times x^2\)
When dealing with the algebraic expression \(3x \times x^2\), we apply the rules of exponents to simplify it.
Steps to Simplify
- Identify the terms to be multiplied: \(3x\) and \(x^2\).
- Apply the product rule for exponents: \(x^a \times x^b = x^{a+b}\).
- In this case, \(3x \times x^2 = 3 \times x^{1+2} = 3x^3\).
Result
The simplified form of \(3x \times x^2\) is \(3x^3\).
Visual Representation
Below is a visual representation of the steps:
| Step | Expression | Explanation |
| Initial | \(3x \times x^2\) | Original expression |
| Simplify | \(3 \times x^{1+2}\) | Apply product rule for exponents |
| Final | \(3x^3\) | Simplified form |
Additional Resources
These tools provide step-by-step solutions to various algebraic problems, helping you understand the process and practice similar problems.
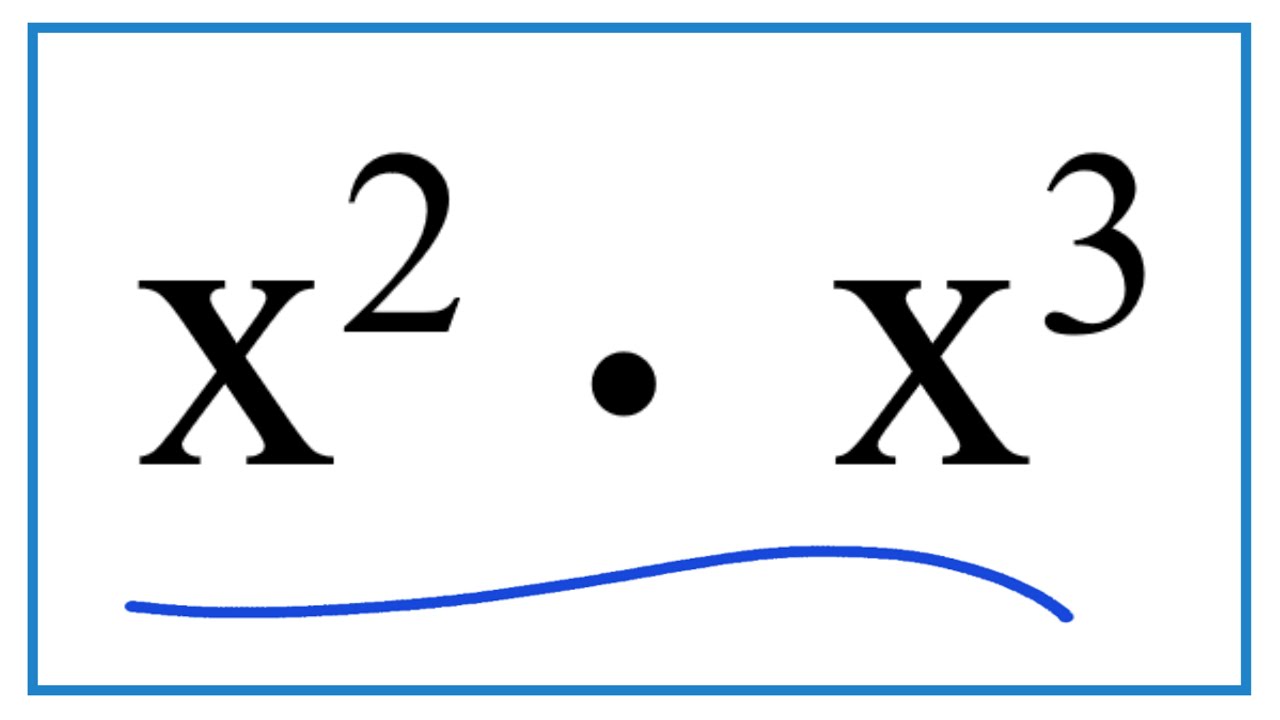
READ MORE:
Understanding Basic Algebraic Expressions
Algebraic expressions are combinations of variables, numbers, and arithmetic operations. They form the foundation for many algebraic principles and methods. Understanding how to manipulate and simplify these expressions is crucial for solving equations and more complex mathematical problems.
Let's break down a basic expression involving multiplication and exponentiation:
- Expression: \( 3x \cdot x^2 \)
- Step-by-Step Simplification:
- Identify the components: The expression consists of a constant (3) and variables with exponents (x and \( x^2 \)).
- Apply the product rule for exponents: When multiplying like bases, you add their exponents. Here, \( x \cdot x^2 \) becomes \( x^{1+2} \) which simplifies to \( x^3 \).
- Combine the constant with the simplified variable expression: Multiply the constant 3 by the resulting \( x^3 \) to get \( 3x^3 \).
- Final Simplified Expression: \( 3x^3 \)
Understanding and simplifying algebraic expressions like this example is fundamental in algebra, helping to solve equations and understand more complex mathematical concepts.
Introduction to Polynomials
Polynomials are fundamental expressions in algebra that involve variables and coefficients. They consist of terms that are added, subtracted, or multiplied, but do not include division by variables. Understanding polynomials is crucial for solving various algebraic equations and understanding higher-level math concepts. Here, we explore the basics of polynomials, including their structure, types, and operations.
Definition and Structure
A polynomial is an expression of the form:
$$a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0$$
where \(a_n, a_{n-1}, ..., a_1, a_0\) are constants (coefficients) and \(x\) is the variable. The highest power of \(x\) is called the degree of the polynomial.
Types of Polynomials
- Monomial: A polynomial with just one term (e.g., \(3x^2\)).
- Binomial: A polynomial with two terms (e.g., \(x^2 - 4\)).
- Trinomial: A polynomial with three terms (e.g., \(x^2 + 5x + 6\)).
Polynomial Operations
There are several key operations that can be performed on polynomials:
- Addition: Combine like terms to add polynomials.
- Subtraction: Subtract by adding the opposite of each term.
- Multiplication: Use the distributive property or FOIL method for binomials.
- Division: Use long division or synthetic division for dividing polynomials.
Example: Multiplying Polynomials
To multiply \(3x \cdot x^2\), follow these steps:
- Identify the terms to be multiplied: \(3x\) and \(x^2\).
- Multiply the coefficients: \(3 \cdot 1 = 3\).
- Add the exponents of like bases: \(x^1 \cdot x^2 = x^{1+2} = x^3\).
Thus, \(3x \cdot x^2 = 3x^3\).
Polynomial Applications
Polynomials are used in various fields such as physics, engineering, and economics to model complex systems and solve practical problems. Mastery of polynomial operations is essential for progressing in these areas.
Simplification Techniques
Simplifying algebraic expressions is a fundamental skill in mathematics that helps in solving equations and understanding functions. Here, we will focus on the simplification techniques for expressions like \(3x \times x^2\).
- Combine Like Terms:
- Identify terms with the same variable and exponent. In \(3x \times x^2\), both terms involve the variable \(x\).
- Use the Product Rule:
- When multiplying terms with the same base, add the exponents. For \(3x \times x^2\), apply the product rule: \[3x \times x^2 = 3x^{1+2} = 3x^3.\]
- Simplify the Expression:
- The simplified form of \(3x \times x^2\) is \(3x^3\). This is the simplest form of the expression where the coefficients are combined, and the exponents are added.
These techniques are essential for handling more complex algebraic expressions and are widely used in various fields of mathematics and science.
Solving Algebraic Equations
Solving algebraic equations involves finding the value of the variable that makes the equation true. This process can include several steps, such as simplifying the equation, isolating the variable, and using algebraic properties. Below is a detailed guide on how to solve algebraic equations effectively.
- Simplify the Equation
- Combine like terms on both sides of the equation.
- Use the distributive property to eliminate parentheses.
- Isolate the Variable
- Move all terms containing the variable to one side of the equation.
- Move all constant terms to the opposite side of the equation.
- Use Algebraic Properties
- Apply the addition or subtraction property of equality to isolate the variable term.
- Apply the multiplication or division property of equality to solve for the variable.
- Check the Solution
- Substitute the solution back into the original equation to verify it satisfies the equation.
Let's solve a sample equation step-by-step:
Example: Solve \(3x \cdot x^2 = 12\)
- Simplify: \(3x \cdot x^2 = 3x^3\), so the equation becomes \(3x^3 = 12\).
- Isolate the variable: Divide both sides by 3 to get \(x^3 = 4\).
- Solve for \(x\): Take the cube root of both sides to find \(x = \sqrt[3]{4}\).
- Check the solution: Substitute \(x = \sqrt[3]{4}\) back into the original equation to verify it works.
By following these steps, you can solve various types of algebraic equations efficiently.

Using Online Calculators
Online calculators are powerful tools that can simplify complex mathematical problems quickly and accurately. They are particularly useful for solving algebraic equations, graphing functions, and performing various calculations. Here’s a step-by-step guide to using online calculators effectively:
-
Select a Reliable Calculator:
Choose a reputable online calculator like Mathway, Desmos, or Microsoft Math Solver. These platforms are known for their accuracy and ease of use.
-
Inputting the Equation:
Enter the algebraic equation or expression into the calculator. For example, for the expression \(3x \times x^2\), you would type it exactly as shown.
-
Understanding the Output:
The calculator will display the solution, often breaking down the steps taken to arrive at the answer. This helps in understanding the process and verifying the correctness of the solution.
-
Utilizing Graphing Features:
Many online calculators, such as Desmos, offer graphing capabilities. You can plot functions and visualize the solutions to equations, which is particularly useful for understanding polynomial equations.
-
Exploring Additional Functions:
Explore additional features such as solving systems of equations, performing matrix operations, and working with trigonometric functions. These tools can handle a wide range of mathematical problems.
Using online calculators can enhance your understanding of algebra and make problem-solving more efficient. They are invaluable resources for students and professionals alike.
Graphical Representation of Equations
Graphical representation of equations helps visualize mathematical relationships. It involves plotting equations on a coordinate plane to better understand their behavior and solutions. Here's a step-by-step guide to graphically represent the equation \(3x \times x^2\):
- Simplify the Equation:
The given equation \(3x \times x^2\) simplifies to \(3x^3\). This is a cubic equation, and its graph will be a curve.
- Create a Table of Values:
Choose a range of x-values and calculate the corresponding y-values using \(y = 3x^3\). For example:
x y = 3x^3 -2 -24 -1 -3 0 0 1 3 2 24 - Plot the Points:
On a graph paper or using an online graphing tool like Desmos, plot the points from the table of values.
- Draw the Curve:
Connect the plotted points with a smooth curve. The graph of \(3x^3\) will show how y changes with x, illustrating the cubic nature of the equation.
- Analyze the Graph:
Observe key features like the intercepts, turning points, and the overall shape. For \(3x^3\), the graph passes through the origin and has symmetry about the origin.
Using these steps, you can effectively represent and analyze the equation \(3x \times x^2\) graphically, gaining deeper insights into its characteristics.
Complex Numbers and Operations
A complex number is a number that can be written in the form \(a + bi\), where \(a\) and \(b\) are real numbers and \(i\) is the imaginary unit, satisfying \(i^2 = -1\). Complex numbers encompass both real and imaginary numbers.
Basic Operations with Complex Numbers
To perform operations with complex numbers, we treat \(i\) as a variable and apply algebraic rules, remembering that \(i^2 = -1\).
Addition and Subtraction
To add or subtract complex numbers, combine the real parts and the imaginary parts separately:
- Addition: \((3 + 4i) + (1 + 2i) = (3 + 1) + (4i + 2i) = 4 + 6i\)
- Subtraction: \((3 + 4i) - (1 + 2i) = (3 - 1) + (4i - 2i) = 2 + 2i\)
Multiplication
Use the distributive property and the fact that \(i^2 = -1\) to multiply complex numbers:
- \((3 + 2i)(1 + 4i) = 3(1) + 3(4i) + 2i(1) + 2i(4i) = 3 + 12i + 2i + 8i^2\)
- Since \(i^2 = -1\), this simplifies to: \(3 + 14i + 8(-1) = 3 + 14i - 8 = -5 + 14i\)
Division
To divide complex numbers, multiply the numerator and the denominator by the conjugate of the denominator:
- \(\frac{3 + 2i}{1 - i}\)
- Multiply by the conjugate: \(\frac{(3 + 2i)(1 + i)}{(1 - i)(1 + i)} = \frac{3 + 3i + 2i + 2i^2}{1 - i^2}\)
- Simplify using \(i^2 = -1\): \(\frac{3 + 5i + 2(-1)}{1 - (-1)} = \frac{3 + 5i - 2}{1 + 1} = \frac{1 + 5i}{2} = \frac{1}{2} + \frac{5}{2}i\)
Complex Conjugates
The complex conjugate of a complex number \(a + bi\) is \(a - bi\). The product of a complex number and its conjugate is always a real number:
- \((a + bi)(a - bi) = a^2 - (bi)^2 = a^2 - b^2(i^2) = a^2 + b^2\)
- Example: \((3 + 4i)(3 - 4i) = 9 + 16 = 25\)
Graphical Representation
Complex numbers can be represented on a complex plane with the x-axis representing the real part and the y-axis representing the imaginary part. A complex number \(a + bi\) corresponds to the point \((a, b)\) on this plane.
Practical Applications
Complex numbers are used in various fields such as engineering, physics, and applied mathematics. They are essential in solving certain differential equations, analyzing electrical circuits, and representing waveforms.
By understanding these operations and their properties, one can effectively work with complex numbers in both theoretical and practical contexts.
Matrix Calculations
Matrices are an essential component of linear algebra and are widely used in various fields such as engineering, physics, computer science, and economics. A matrix is a rectangular array of numbers arranged in rows and columns. Here, we will explore some fundamental matrix calculations including addition, subtraction, multiplication, and the determination of the determinant and inverse of a matrix.
Matrix Addition and Subtraction
Matrix addition and subtraction are performed element-wise. For two matrices to be added or subtracted, they must have the same dimensions.
Consider matrices \( A \) and \( B \) with the same dimensions:
\[
A = \begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}
\quad \text{and} \quad
B = \begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{pmatrix}
\]
The sum \( C = A + B \) is given by:
\[
C = \begin{pmatrix}
a_{11} + b_{11} & a_{12} + b_{12} \\
a_{21} + b_{21} & a_{22} + b_{22}
\end{pmatrix}
\]
Matrix Multiplication
Matrix multiplication is more complex than addition or subtraction. The number of columns in the first matrix must equal the number of rows in the second matrix.
Consider matrices \( A \) and \( B \) as follows:
\[
A = \begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}
\quad \text{and} \quad
B = \begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{pmatrix}
\]
The product \( C = AB \) is given by:
\[
C = \begin{pmatrix}
a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} \\
a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22}
\end{pmatrix}
\]
Determinant of a Matrix
The determinant is a scalar value that can be computed from the elements of a square matrix. It provides important properties about the matrix, such as whether it is invertible.
For a 2x2 matrix \( A \), the determinant is given by:
\[
\text{det}(A) = \begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{vmatrix} = a_{11}a_{22} - a_{12}a_{21}
\]
Inverse of a Matrix
The inverse of a matrix \( A \) is another matrix \( A^{-1} \) such that \( AA^{-1} = I \), where \( I \) is the identity matrix. Not all matrices have inverses. A matrix must be square and have a non-zero determinant to have an inverse.
The inverse of a 2x2 matrix \( A \) is given by:
\[
A^{-1} = \frac{1}{\text{det}(A)} \begin{pmatrix}
a_{22} & -a_{12} \\
-a_{21} & a_{11}
\end{pmatrix}
\]
Example Calculation
Let's consider the following matrices:
\[
A = \begin{pmatrix}
1 & 2 \\
3 & 4
\end{pmatrix}
\quad \text{and} \quad
B = \begin{pmatrix}
5 & 6 \\
7 & 8
\end{pmatrix}
\]
Matrix addition \( C = A + B \) is:
\[
C = \begin{pmatrix}
1+5 & 2+6 \\
3+7 & 4+8
\end{pmatrix} = \begin{pmatrix}
6 & 8 \\
10 & 12
\end{pmatrix}
\]
Matrix multiplication \( D = AB \) is:
\[
D = \begin{pmatrix}
1 \cdot 5 + 2 \cdot 7 & 1 \cdot 6 + 2 \cdot 8 \\
3 \cdot 5 + 4 \cdot 7 & 3 \cdot 6 + 4 \cdot 8
\end{pmatrix} = \begin{pmatrix}
19 & 22 \\
43 & 50
\end{pmatrix}
\]
Determinant of \( A \) is:
\[
\text{det}(A) = 1 \cdot 4 - 2 \cdot 3 = 4 - 6 = -2
\]
Inverse of \( A \) is:
\[
A^{-1} = \frac{1}{-2} \begin{pmatrix}
4 & -2 \\
-3 & 1
\end{pmatrix} = \begin{pmatrix}
-2 & 1 \\
1.5 & -0.5
\end{pmatrix}
\]

Calculus and its Applications
Calculus is a branch of mathematics that studies continuous change. It is divided into two main branches: differential calculus and integral calculus. Differential calculus deals with the rate of change and slopes of curves, while integral calculus concerns the accumulation of quantities and areas under and between curves. Calculus has a wide range of applications in various fields such as physics, engineering, economics, statistics, and more.
Fundamental Concepts
- Limits: The concept of limits is fundamental in calculus. It defines the value that a function approaches as the input approaches some value.
- Derivatives: Derivatives represent the rate of change of a function with respect to a variable. The derivative of a function \( f(x) \) is denoted as \( f'(x) \) or \( \frac{df}{dx} \).
- Integrals: Integrals are the inverse operation of derivatives. The integral of a function represents the accumulation of a quantity over an interval. It is denoted as \( \int f(x) \, dx \).
Calculating Derivatives
To find the derivative of a function, we use various rules and techniques:
- Power Rule: For any real number \( n \), the derivative of \( x^n \) is \( nx^{n-1} \).
- Product Rule: For functions \( u(x) \) and \( v(x) \), the derivative of their product is \( u'(x)v(x) + u(x)v'(x) \).
- Quotient Rule: For functions \( u(x) \) and \( v(x) \), the derivative of their quotient is \( \frac{u'(x)v(x) - u(x)v'(x)}{[v(x)]^2} \).
- Chain Rule: For composite functions \( f(g(x)) \), the derivative is \( f'(g(x)) \cdot g'(x) \).
Example
Consider the function \( f(x) = 3x^2 \). To find the derivative, we apply the power rule:
\[
f'(x) = \frac{d}{dx}(3x^2) = 3 \cdot 2x^{2-1} = 6x
\]
Calculating Integrals
Integrals can be calculated using different techniques such as substitution, integration by parts, and partial fractions. The basic integral formulas include:
- Power Rule for Integration: For any real number \( n \neq -1 \), the integral of \( x^n \) is \( \frac{x^{n+1}}{n+1} + C \), where \( C \) is the constant of integration.
- Definite Integral: The definite integral of \( f(x) \) from \( a \) to \( b \) is denoted as \( \int_a^b f(x) \, dx \) and represents the area under the curve from \( x = a \) to \( x = b \).
Example
Consider the function \( f(x) = 3x^2 \). To find the integral, we apply the power rule for integration:
\[
\int 3x^2 \, dx = 3 \cdot \frac{x^{2+1}}{2+1} + C = x^3 + C
\]
Applications of Calculus
Calculus has numerous applications in various fields:
- Physics: Calculus is used to model motion, including velocity and acceleration, and to describe the behavior of physical systems.
- Engineering: It helps in designing and analyzing systems and structures, optimizing processes, and solving differential equations that describe engineering problems.
- Economics: Calculus is used to find optimal solutions, model economic growth, and analyze changes in market conditions.
- Biology: It aids in modeling population dynamics, spread of diseases, and rates of biological processes.
- Computer Science: Calculus is used in algorithms, computer graphics, and machine learning to optimize and analyze systems.
Statistics in Algebra
Statistics is an essential component of algebra, providing tools to analyze and interpret data. In algebra, statistical concepts help us understand patterns, trends, and relationships within datasets. This section will cover key statistical concepts and their applications in algebra.
Key Statistical Concepts
- Mean (Average): The sum of all values divided by the number of values. Represented as \( \bar{x} \).
- Median: The middle value in a dataset when the values are arranged in ascending order. If the dataset has an even number of values, the median is the average of the two middle numbers.
- Mode: The value that appears most frequently in a dataset.
- Range: The difference between the highest and lowest values in a dataset.
- Variance: A measure of how much the values in a dataset vary from the mean. It is calculated as the average of the squared differences from the mean.
- Standard Deviation: The square root of the variance, providing a measure of the dispersion or spread of the dataset.
Applications in Algebra
Statistics in algebra is applied in various ways, such as solving real-world problems, making predictions, and conducting data analysis. Here are some examples:
1. Solving Real-World Problems
Algebraic equations often incorporate statistical data to model real-world scenarios. For example, predicting future sales based on past performance data involves calculating the mean, variance, and standard deviation of sales figures.
2. Making Predictions
Statistical methods such as regression analysis help in making predictions by identifying relationships between variables. For example, a linear regression model can predict a student's future test scores based on their past performance.
3. Data Analysis
Algebraic formulas and statistical measures are used to analyze data and extract meaningful insights. For instance, the mean and standard deviation are used to summarize and understand the distribution of data points in a survey.
Example Problems
- Calculating the Mean:
Given the dataset: \( 4, 8, 6, 5, 3, 7 \), the mean is calculated as:
\[
\bar{x} = \frac{4 + 8 + 6 + 5 + 3 + 7}{6} = \frac{33}{6} = 5.5
\] - Finding the Median:
For the dataset: \( 3, 5, 7, 8, 9 \), the median is:
\[
\text{Median} = 7
\] - Determining the Mode:
Given the dataset: \( 2, 4, 4, 6, 8, 4, 9 \), the mode is:
\[
\text{Mode} = 4
\] - Calculating Variance and Standard Deviation:
For the dataset: \( 2, 4, 4, 6, 8, 4, 9 \), the variance (\( \sigma^2 \)) and standard deviation (\( \sigma \)) are calculated as:
\[
\sigma^2 = \frac{(2-5.29)^2 + (4-5.29)^2 + (4-5.29)^2 + (6-5.29)^2 + (8-5.29)^2 + (4-5.29)^2 + (9-5.29)^2}{7} = 5.76
\]\[
\sigma = \sqrt{5.76} = 2.4
\]
Conclusion
Understanding statistics within the context of algebra enhances problem-solving skills and enables the effective analysis of data. By mastering these statistical concepts, one can apply algebraic methods to various fields, including science, economics, and social studies.
Step-by-Step Algebra Examples
Understanding algebra involves working through various types of problems step by step. Here, we will explore some common types of algebraic problems and their solutions.
Example 1: Simplifying Expressions
Simplify the expression \(3x \cdot x^2\).
- Identify the terms and their exponents:
- First term: \(3x\)
- Second term: \(x^2\)
- Multiply the coefficients and add the exponents of like bases:
- Coefficient: \(3\)
- Exponent of \(x\): \(1 + 2 = 3\)
- Result: \(3x^3\)
So, \(3x \cdot x^2 = 3x^3\).
Example 2: Solving Linear Equations
Solve for \(x\) in the equation \(2x + 3 = 11\).
- Subtract 3 from both sides:
\[
2x + 3 - 3 = 11 - 3
\]
This simplifies to \(2x = 8\).
- Divide both sides by 2:
\[
\frac{2x}{2} = \frac{8}{2}
\]
This simplifies to \(x = 4\).
Therefore, the solution is \(x = 4\).
Example 3: Solving Quadratic Equations
Solve the quadratic equation \(x^2 - 5x + 6 = 0\).
- Factor the quadratic expression: \[ x^2 - 5x + 6 = (x - 2)(x - 3) \]
- Set each factor to zero and solve for \(x\):
- \(x - 2 = 0 \implies x = 2\)
- \(x - 3 = 0 \implies x = 3\)
Therefore, the solutions are \(x = 2\) and \(x = 3\).
Example 4: Simplifying Rational Expressions
Simplify the rational expression \(\frac{3x^2 + 6x}{3x}\).
- Factor out the greatest common factor (GCF) in the numerator: \[ 3x^2 + 6x = 3x(x + 2) \]
- Cancel the common factor in the numerator and the denominator: \[ \frac{3x(x + 2)}{3x} = x + 2 \]
So, \(\frac{3x^2 + 6x}{3x} = x + 2\).
Example 5: Solving Systems of Equations
Solve the system of equations:
\[
\begin{cases}
2x + y = 5 \\
x - y = 1
\end{cases}
\]
- Add the two equations to eliminate \(y\):
\[
(2x + y) + (x - y) = 5 + 1
\]
This simplifies to \(3x = 6\).
- Solve for \(x\): \[ x = 2 \]
- Substitute \(x = 2\) into the second equation to solve for \(y\): \[ 2 - y = 1 \implies y = 1 \]
Therefore, the solution is \(x = 2\) and \(y = 1\).
These examples illustrate the step-by-step process of solving various types of algebraic problems. Practice and familiarity with these steps will improve your algebra skills.
Additional Mathematical Concepts
In this section, we will explore a variety of additional mathematical concepts that extend beyond basic algebra and into more advanced areas. These topics provide a foundation for higher-level mathematics and its applications.
1. Exponential and Logarithmic Functions
Exponential functions involve expressions where the variable is in the exponent, such as \( f(x) = a^x \). These functions grow rapidly and are essential in fields such as biology, finance, and physics.
Logarithmic functions are the inverses of exponential functions. The logarithm of a number is the exponent to which the base must be raised to produce that number. For example, \( \log_b(x) = y \) means \( b^y = x \).
2. Trigonometry
Trigonometry is the study of relationships between the angles and sides of triangles. Key functions include sine (\(\sin\)), cosine (\(\cos\)), and tangent (\(\tan\)). These functions are crucial in fields such as engineering, physics, and computer graphics.
- Sine Function: \( \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} \)
- Cosine Function: \( \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} \)
- Tangent Function: \( \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} \)
3. Complex Numbers
Complex numbers extend the idea of one-dimensional number lines to the complex plane using the imaginary unit \( i \), where \( i^2 = -1 \). A complex number is expressed as \( a + bi \), where \( a \) and \( b \) are real numbers.
Complex numbers are used in engineering, physics, and applied mathematics to solve problems involving oscillations and waveforms.
4. Sequences and Series
Sequences are ordered lists of numbers, while series are the sum of the terms of a sequence. For example, the arithmetic sequence \( a, a+d, a+2d, \ldots \) has a common difference \( d \), and the geometric sequence \( a, ar, ar^2, \ldots \) has a common ratio \( r \).
- Arithmetic Series: \( S_n = \frac{n}{2}(a + l) \)
- Geometric Series: \( S_n = a \frac{1-r^n}{1-r} \)
5. Probability and Statistics
Probability measures the likelihood of an event occurring, while statistics involves the collection, analysis, interpretation, and presentation of data. Key concepts include mean, median, mode, variance, and standard deviation.
Probability and statistics are widely used in fields such as science, economics, and social sciences to make informed decisions based on data.
- Mean: \( \mu = \frac{1}{N} \sum_{i=1}^N x_i \)
- Variance: \( \sigma^2 = \frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2 \)
- Standard Deviation: \( \sigma = \sqrt{\sigma^2} \)
6. Differential Equations
Differential equations involve functions and their derivatives and are used to model real-world phenomena where rates of change are involved. These equations are foundational in physics, engineering, and other applied sciences.
An example of a simple differential equation is \( \frac{dy}{dx} = ky \), which describes exponential growth or decay.
7. Linear Algebra
Linear algebra studies vectors, vector spaces, and linear transformations. Key concepts include matrices, determinants, eigenvalues, and eigenvectors. Linear algebra is fundamental in computer science, physics, and economics.
- Matrix Multiplication: \( (AB)_{ij} = \sum_{k} A_{ik} B_{kj} \)
- Determinant of a Matrix: For a \( 2 \times 2 \) matrix \( A \), \( \det(A) = ad - bc \) where \( A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \)
8. Calculus
Calculus deals with limits, derivatives, integrals, and infinite series. It is used to study changes in functions and is fundamental in physics, engineering, economics, and many other fields.
Key concepts include the derivative, which measures the rate of change, and the integral, which measures the accumulation of quantities.
- Derivative: \( f'(x) = \lim_{{h \to 0}} \frac{f(x+h) - f(x)}{h} \)
- Integral: \( \int_a^b f(x) \, dx \)
These additional mathematical concepts provide essential tools for understanding and solving complex problems in various scientific and engineering disciplines.
Mathematical Problem Solving Techniques
Effective mathematical problem-solving requires a systematic approach. Below are detailed steps and techniques to enhance your problem-solving skills:
- Understand the Problem:
- Read the problem carefully and identify what is being asked.
- Determine the knowns and unknowns.
- Visualize the problem using diagrams or graphs if necessary.
- Devise a Plan:
- Choose a strategy to solve the problem such as:
- Breaking the problem into smaller parts
- Using algebraic techniques like factoring or expanding
- Applying formulas or theorems
- Consider multiple approaches and select the most efficient one.
- Choose a strategy to solve the problem such as:
- Carry Out the Plan:
- Execute the chosen strategy step by step.
- Maintain clear and organized work to avoid mistakes.
- Review and Check:
- Verify each step of your solution.
- Check if the answer makes sense in the context of the problem.
- Recalculate if necessary to ensure accuracy.
Let's consider an example to illustrate these techniques:
Example: Solve the Equation \(3x \cdot x^2 = 27\)
- Understand the Problem:
- We need to solve for \(x\) in the equation \(3x \cdot x^2 = 27\).
- The equation represents a multiplication of terms involving \(x\).
- Devise a Plan:
- Combine the terms involving \(x\): \[ 3x \cdot x^2 = 3x^3 \]
- Set up the equation to isolate \(x\): \[ 3x^3 = 27 \]
- Carry Out the Plan:
- Divide both sides by 3 to simplify: \[ x^3 = 9 \]
- Take the cube root of both sides to solve for \(x\): \[ x = \sqrt[3]{9} \approx 2.08 \]
- Review and Check:
- Substitute \(x \approx 2.08\) back into the original equation to verify: \[ 3 \cdot 2.08 \cdot (2.08)^2 \approx 27 \]
- Ensure that the approximation is close to the original value.
By following these steps, you can approach and solve algebraic problems systematically and effectively.
Applications in Real-World Scenarios
Understanding how algebraic expressions and functions apply to real-world scenarios can enhance our grasp of mathematical concepts and their practical significance. Here, we explore several applications of algebra in various fields:
-
Quadratic Functions in Architecture and Engineering
Quadratic functions often describe the parabolic shapes seen in architecture and engineering, such as arches and bridges. For instance, the equation \( y = ax^2 + bx + c \) can represent the shape of a parabolic arch, where the vertex denotes the highest point. These functions help in determining structural stability and aesthetic design.
-
Maximizing Revenue
Businesses use quadratic functions to model and maximize revenue. If a company's revenue \( R \) is a function of the number of units sold \( x \), such as \( R(x) = ax^2 + bx + c \), finding the vertex of the parabola \( x = -\frac{b}{2a} \) helps identify the optimal number of units to sell for maximum profit.
-
Projectile Motion
In physics, the trajectory of a projectile is often modeled by a quadratic function. The height \( h \) of a projectile at time \( t \) can be described by \( h(t) = -16t^2 + vt + h_0 \), where \( v \) is the initial velocity and \( h_0 \) is the initial height. This function helps in calculating the maximum height and range of the projectile.
-
Optimization Problems
Quadratic functions are essential in optimization problems. For example, determining the dimensions of a garden to maximize area given a fixed perimeter involves setting up a quadratic equation and finding its maximum value. If the garden has length \( l \) and width \( w \), and the perimeter is fixed, the area \( A \) can be maximized by solving \( A = lw \) subject to the perimeter constraint.
-
Economics and Cost Functions
In economics, cost functions are often quadratic. The total cost \( C \) of producing \( x \) items might be represented as \( C(x) = ax^2 + bx + c \). Finding the minimum point of this function helps businesses minimize production costs and improve efficiency.
These examples illustrate how algebra, particularly quadratic functions, plays a crucial role in solving practical problems across various disciplines, from engineering and physics to business and economics.
Interactive Learning Tools
Interactive learning tools are essential for enhancing the understanding and application of algebraic concepts such as \(3x \times x^2\). These tools offer dynamic and visual ways to engage with mathematical problems and solutions.
Graphing Calculators
Graphing calculators, such as those offered by , , and , allow students to plot functions, visualize equations, and interact with graphs.
- Desmos: Known for its intuitive interface and powerful graphing capabilities. Users can plot functions, adjust parameters with sliders, and see real-time changes.
- GeoGebra: Offers comprehensive tools for graphing and geometry. It supports interactive learning through dynamic graphs and visual aids.
- Symbolab: Provides step-by-step solutions alongside graphing capabilities, making it easier to understand complex algebraic expressions.
Step-by-Step Solvers
Platforms like and provide detailed, step-by-step solutions to algebraic problems, including the simplification and solving of expressions like \(3x \times x^2 = 3x^3\).
- Enter the algebraic expression into the solver.
- The tool breaks down each step, showing the multiplication of coefficients and the addition of exponents.
- Visual aids and graphs can be generated to further illustrate the solution.
Interactive Activities
Interactive activities available on platforms like Desmos engage students with hands-on learning experiences. These activities often include:
- Manipulatives: Virtual objects that students can move and adjust to understand algebraic concepts better.
- Simulations: Interactive simulations that demonstrate how algebraic principles apply to real-world scenarios.
Benefits of Interactive Learning Tools
Using these tools, students can:
- Gain a deeper understanding of algebraic concepts through visual and interactive means.
- Receive immediate feedback on their work, helping to identify and correct mistakes.
- Explore algebra in a more engaging and less intimidating environment.
Overall, interactive learning tools are invaluable for making algebra more accessible and enjoyable. By leveraging these resources, students can enhance their problem-solving skills and build a stronger foundation in mathematics.
Advanced Algebra Topics
Advanced algebra covers a wide range of topics that extend beyond basic algebraic principles. Here, we will delve into some of the key areas that are fundamental to advanced algebra.
- Polynomials
Polynomials are expressions consisting of variables and coefficients, combined using addition, subtraction, and multiplication. For example, the polynomial \(3x^2 + 2x - 5\) can be manipulated in various ways, such as factoring and expanding.
- Factoring: The process of breaking down a polynomial into simpler terms that, when multiplied together, give the original polynomial. For instance, \(x^2 - 5x + 6\) factors into \((x - 2)(x - 3)\).
- Expanding: Distributing the terms in a polynomial to remove parentheses. For example, \((x + 2)(x - 3)\) expands to \(x^2 - x - 6\).
- Quadratic Equations
A quadratic equation is a second-degree polynomial equation in the form \(ax^2 + bx + c = 0\). These can be solved using various methods such as factoring, completing the square, and the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\] - Inequalities
Inequalities involve expressions where two sides are not necessarily equal, using signs such as \(>\), \(<\), \(\geq\), and \(\leq\). Solving inequalities often involves finding the range of values that satisfy the condition.
- Systems of Equations
These involve solving for multiple variables across several equations. Methods include substitution, elimination, and using matrices. For example, solving the system:
\[
\begin{cases}
2x + 3y = 6 \\
x - y = 2
\end{cases}
\]
can be approached by substitution or elimination to find the values of \(x\) and \(y\). - Matrices
Matrices are arrays of numbers that can be used to represent and solve systems of linear equations. Operations include addition, subtraction, multiplication, and finding determinants and inverses.
- Addition: Adding corresponding elements of matrices of the same dimension.
- Multiplication: Multiplying rows of the first matrix by columns of the second matrix.
- Determinants: A scalar value that can be computed from the elements of a square matrix, important in solving linear systems.
- Inverses: A matrix that, when multiplied by the original matrix, results in the identity matrix.
- Complex Numbers
Complex numbers are numbers in the form \(a + bi\), where \(i\) is the imaginary unit with the property that \(i^2 = -1\). Operations on complex numbers include addition, subtraction, multiplication, and division.
These advanced algebra topics form the foundation for more complex mathematical concepts and applications. Mastery of these areas is essential for further studies in mathematics, engineering, physics, and related fields.

Resources and References
For further reading and deeper understanding of the topics covered in this guide, the following resources are highly recommended:
- : Comprehensive tutorials and practice exercises on basic to advanced algebraic concepts.
- : A great resource for learning and practicing algebra, offering clear explanations and examples.
- : User-friendly site that explains algebraic concepts with interactive tools and fun activities.
- : An advanced computational tool that can solve algebraic equations and show step-by-step solutions.
- : Online calculator that provides step-by-step solutions for algebraic equations, integrals, and more.
- : An online graphing calculator that helps visualize algebraic equations and functions.
- : Free course materials from MIT's mathematics courses, including lectures on algebra.
For reference books, consider the following:
- Algebra I For Dummies by Mary Jane Sterling: A comprehensive guide for beginners, covering all essential topics in a clear and accessible manner.
- The Art of Problem Solving, Volume 1 by Richard Rusczyk: A resourceful book for those looking to enhance their problem-solving skills in algebra and beyond.
- College Algebra by Michael Sullivan: A widely used textbook offering a deep dive into college-level algebra concepts.
For those who prefer interactive learning, these tools can be very helpful:
- : An interactive geometry, algebra, statistics, and calculus application.
- : Offers lessons, solvers, and worksheets for a variety of algebraic topics.
Engaging with online communities can also provide support and enhance learning:
- : A Q&A site for math enthusiasts to ask and answer questions.
- : A community for discussing math problems and concepts.
For additional academic support, these university resources can be useful:
- : Detailed notes and tutorials on various math topics by Lamar University.
- : Access to resources and lectures from one of the leading mathematics departments.
Video hướng dẫn cách bình phương biểu thức: (3x)^2 và (3+x)^2, chi tiết và dễ hiểu cho người học toán.
Cách bình phương: (3x)^2 so với (3+x)^2
READ MORE:
Video hướng dẫn cách tích phân biểu thức x căn bậc hai của 3x dx, dễ hiểu và chi tiết cho người học toán.
Tích phân x căn bậc hai của 3x dx
x-1=sec(squared)x.jpg)