Topic x squared: X squared, a fundamental concept in mathematics, holds profound significance across various disciplines. This comprehensive guide explores its definition, properties, applications in quadratic equations, graphical representations, common misconceptions, and advanced theoretical extensions. Whether you're a student, educator, or enthusiast, delve into the complexities and elegance of X squared, unraveling its mysteries and practical implications.
Table of Content
- X Squared: Understanding and Applications
- Introduction to X Squared
- Definition and Basic Concepts
- Examples and Applications
- Perfect Squares and Properties
- Square Root of X Squared
- X Squared in Quadratic Equations
- Graphical Representation of X Squared
- Common Mistakes and Misconceptions
- Advanced Topics: X Squared in Higher Mathematics
- Frequently Asked Questions
- YOUTUBE: Hướng dẫn chi tiết cách giải phương trình x bình phương = 4 và khám phá các giá trị bình phương khác của x.
X Squared: Understanding and Applications
The concept of \(x^2\), or x squared, is a fundamental element in mathematics, encompassing various aspects from basic arithmetic to complex algebra and geometry. Here, we explore the definition, calculation, and applications of \(x^2\).
Definition of X Squared
X squared, denoted as \(x^2\), refers to a number \(x\) multiplied by itself. Mathematically, it is expressed as:
\[
x^2 = x \times x
\]
Examples and Calculations
- Example 1: If \(x\) is 7, then \(x^2 = 7 \times 7 = 49\).
- Example 2: For \(x = -3\), \(x^2 = (-3) \times (-3) = 9\).
- Example 3: \(x^2 + x^2 = 2x^2\).
- Example 4: \(x^2 \times x^2 = x^4\).
Properties of X Squared
- Perfect Squares: A number obtained by squaring an integer is called a perfect square.
- Square Roots: The square root of \(x^2\) is \(\sqrt{x^2} = |x|\).
Applications in Quadratic Equations
Quadratic equations are a significant application of \(x^2\). A general quadratic equation is of the form:
\[
ax^2 + bx + c = 0
\]
The solutions to this equation are given by the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Visual Representation
Graphically, \(x^2\) forms a parabola. This U-shaped curve is symmetrical about the y-axis and opens upwards if the coefficient of \(x^2\) is positive.
Differences Between X and X Squared
The key difference between \(x\) and \(x^2\) lies in their mathematical operations and impacts on graphs:
- \(x\) represents a linear relationship, producing a straight line when graphed.
- \(x^2\) represents a quadratic relationship, producing a parabolic curve when graphed.
Real-World Applications
- Calculating Areas: In geometry, the area of a square with side length \(x\) is \(x^2\).
- Physics and Engineering: Quadratic equations involving \(x^2\) model various phenomena such as projectile motion and structural loads.
Conclusion
Understanding \(x^2\) is crucial for advancing in mathematics and related fields. It provides a foundation for solving quadratic equations, analyzing geometric shapes, and modeling real-world scenarios. Continue exploring and practicing to deepen your mathematical knowledge and skills.

READ MORE:
Introduction to X Squared
The expression X squared refers to a number or variable multiplied by itself. It is represented mathematically as X2 or using MathJax as \( X^2 \). This concept is fundamental in various fields of mathematics and science, forming the basis for more complex operations and theories.
In its simplest form, if X is a number, then X2 is the result of multiplying X by itself:
\[ X^2 = X \times X \]
For example:
- If
X = 2, then22 = 4. - If
X = 5, then52 = 25. - If
X = -3, then(-3)2 = 9.
Understanding the concept of squaring a number is crucial because it extends to various applications in algebra, geometry, and calculus. For instance, squaring is a key operation when working with quadratic equations, calculating areas of squares, and analyzing parabolic curves.
The graphical representation of X2 is a parabola opening upwards, with its vertex at the origin (0,0). This is important in visualizing how the values of X affect the square, which is useful in both theoretical and applied mathematics.
Overall, mastering the concept of X squared provides a solid foundation for further mathematical exploration and problem-solving.
Definition and Basic Concepts
In mathematics, "x squared" is represented as \( x^2 \), which means \( x \) is multiplied by itself. This operation is known as squaring a number. For example, if \( x = 3 \), then \( x^2 = 3 \times 3 = 9 \).
Squaring a value is a fundamental operation with several key properties and concepts:
- Definition: The expression \( x^2 \) denotes the product of \( x \) with itself. Mathematically, \( x^2 = x \times x \).
- Positive Result: The square of any real number (positive or negative) is always non-negative. For instance, \( (-4)^2 = 16 \).
- Graphical Representation: The graph of the function \( y = x^2 \) is a parabola opening upwards with its vertex at the origin (0, 0). This parabola is symmetric about the y-axis.
- Perfect Squares: Perfect squares are integers that can be expressed as the square of another integer. For example, 1, 4, 9, 16, and 25 are perfect squares (1 = \( 1^2 \), 4 = \( 2^2 \), 9 = \( 3^2 \), 16 = \( 4^2 \), and 25 = \( 5^2 \)).
Here are some fundamental properties of \( x^2 \):
| Property | Description |
|---|---|
| Domain | All real numbers (\( -\infty, \infty \)) |
| Range | All non-negative real numbers ([0, \(\infty\))) |
| Symmetry | Symmetric about the y-axis (even function) |
| Vertex | (0, 0) |
To understand the concept of squaring in practical terms, consider the area of a square. If the length of each side of a square is \( x \), the area of the square is \( x^2 \). For example, if the side length is 5 units, the area is \( 5^2 = 25 \) square units.
Understanding \( x^2 \) is crucial in various fields of mathematics, including algebra, geometry, and calculus. It forms the basis for quadratic equations, which can be written in the standard form \( ax^2 + bx + c = 0 \). Solving these equations often involves finding the values of \( x \) that satisfy the equation, which can be done using methods such as factoring, completing the square, or the quadratic formula.
Overall, the concept of \( x^2 \) is a foundational element in mathematics, representing a simple yet powerful operation that extends into many advanced topics.
Examples and Applications
X squared, represented as \( x^2 \), is a fundamental concept in mathematics with numerous examples and applications. Below are detailed explanations of various instances where \( x^2 \) is used, along with step-by-step solutions.
Basic Examples
- Example 1: If \( x = 3 \), then \( x^2 = 3^2 = 9 \).
- Example 2: For \( x = -4 \), we have \( x^2 = (-4)^2 = 16 \).
Applications in Geometry
One of the most common applications of \( x^2 \) is in calculating the area of a square.
- Example 3: If each side of a square is \( x \) units long, then the area \( A \) is given by \( A = x^2 \). For a square with side length 5 units, the area is \( 5^2 = 25 \) square units.
Applications in Algebra
In algebra, \( x^2 \) appears frequently in quadratic equations, which are equations of the form \( ax^2 + bx + c = 0 \).
- Example 4: Consider the quadratic equation \( x^2 - 4 = 0 \). Solving for \( x \) involves finding the values of \( x \) that satisfy the equation:
- \( x^2 - 4 = 0 \)
- \( x^2 = 4 \)
- \( x = \pm 2 \)
- Example 5: For a more complex quadratic equation \( 2x^2 - 5x + 2 = 0 \), solving using the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) yields the solutions for \( x \).
Applications in Real Life
Squares and their properties are not limited to theoretical problems. They have real-world applications as well.
- Example 6: Calculating the area of square-shaped plots in land surveying.
- Example 7: Determining the size of square tiles needed to cover a floor area.
Advanced Applications
In advanced mathematics, \( x^2 \) is crucial in various fields such as calculus and higher algebra.
- Example 8: In calculus, the function \( f(x) = x^2 \) is used to study limits, derivatives, and integrals.
- Example 9: In physics, equations involving \( x^2 \) describe parabolic trajectories of projectiles under gravity.
Understanding \( x^2 \) and its applications provides a strong foundation for further studies in mathematics and its real-world applications.
Perfect Squares and Properties
A perfect square is a number that is the product of an integer multiplied by itself. It is represented as \( n^2 \) where \( n \) is an integer. For example, \( 16 \) is a perfect square because it can be expressed as \( 4 \times 4 \) or \( 4^2 \).
Properties of Perfect Squares
- The square root of a perfect square is always an integer.
- A perfect square always ends in 0, 1, 4, 5, 6, or 9. Numbers ending in 2, 3, 7, or 8 are not perfect squares.
- The square of even numbers is always even, and the square of odd numbers is always odd.
- If a number has 1 or 9 in the one's place, its square ends in 1. If it has 4 or 6, its square ends in 6, and if it has 5, its square ends in 5.
Examples of Perfect Squares
| Integer (n) | Perfect Square (n2) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
Identifying Perfect Squares
To check whether a number is a perfect square, you can calculate its square root. If the square root is a whole number, the original number is a perfect square. For example, the square root of 81 is 9, which is a whole number, so 81 is a perfect square.
Applications of Perfect Squares
- In geometry, the area of a square is a perfect square because it is calculated by squaring the length of its side.
- In algebra, perfect squares are used to solve quadratic equations and to factor expressions.
- Perfect squares are also used in statistical formulas and probability calculations.
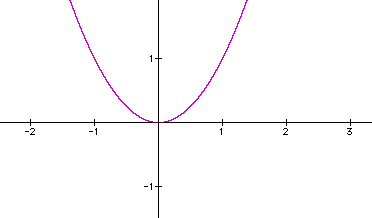
Square Root of X Squared
The square root of \(x^2\) is a fundamental concept in algebra, involving the simplification of radical expressions. When we consider the square root of \(x^2\), it is important to understand both the principal square root and the nature of absolute values.
Mathematically, the square root of \(x^2\) can be expressed as:
\[\sqrt{x^2} = |x|\]
This is because the square root function returns the non-negative value of the square root. Therefore, regardless of whether \(x\) is positive or negative, the result is always the positive value.
Principal Square Root
The principal square root is defined as the non-negative root of a number. For \(x^2\), the principal square root is \(x\) itself if \(x\) is positive or zero:
\[\sqrt{x^2} = x \quad \text{if} \; x \geq 0\]
Handling Negative Values
When \(x\) is negative, the square root function still returns a positive value because it takes the absolute value:
\[\sqrt{x^2} = -x \quad \text{if} \; x < 0\]
Combining these cases, we use the absolute value notation:
\[\sqrt{x^2} = |x|\]
Examples
- For \(x = 3\):
- \[\sqrt{3^2} = \sqrt{9} = 3\]
- For \(x = -4\):
- \[\sqrt{(-4)^2} = \sqrt{16} = 4\]
Applications
Understanding the square root of \(x^2\) is crucial in various mathematical contexts, such as solving quadratic equations and simplifying expressions. In quadratic equations, knowing that \(x = \pm \sqrt{a}\) helps in finding both the positive and negative roots of the equation \(x^2 = a\).
Additionally, the concept of the absolute value plays a significant role in piecewise functions and inequalities, where expressions involving the square root of \(x^2\) frequently occur.
X Squared in Quadratic Equations
Quadratic equations are fundamental in algebra and have the general form:
, where .
Here, , , and are constants, and is the variable. The term is referred to as 'x squared'.
Solving Quadratic Equations
There are several methods to solve quadratic equations:
- Factoring: Expressing the quadratic equation as a product of two binomials.
- Using the Quadratic Formula: A universal method that works for any quadratic equation.
- Completing the Square: A technique to transform the equation into a perfect square trinomial.
- Graphing: Plotting the quadratic function to find the points where it intersects the x-axis.
The Quadratic Formula
The quadratic formula is:
This formula provides the solutions to the quadratic equation by substituting the values of , , and from the equation.
Examples
Consider the quadratic equation:
Here, , , and . Using the quadratic formula:
Solving this, we get:
Thus, the solutions are:
or
Properties of Quadratic Equations
Quadratic equations are characterized by the following properties:
- The graph of a quadratic equation is a parabola.
- The parabola opens upwards if is positive, and downwards if is negative.
- The axis of symmetry of the parabola is given by .
- The vertex of the parabola, the maximum or minimum point, can be found using the axis of symmetry.
Understanding and solving quadratic equations is essential in various fields such as physics, engineering, and finance. Mastery of these techniques provides a strong foundation for more advanced mathematical concepts.
Graphical Representation of X Squared
The graphical representation of \( x^2 \) is a parabola, a symmetrical curve that opens upwards. This shape is fundamental in algebra and appears frequently in various mathematical contexts.
To understand the graph of \( x^2 \), let's delve into its properties and the steps involved in graphing it:
- Standard Form: The quadratic function is generally expressed as \( y = x^2 \). This is the simplest form of a quadratic equation, where the coefficient of \( x^2 \) is 1, and there are no linear or constant terms.
- Vertex: The vertex of the parabola \( y = x^2 \) is at the origin, (0, 0). This is the point where the curve changes direction.
- Axis of Symmetry: The parabola is symmetrical about the y-axis. The axis of symmetry is the vertical line \( x = 0 \).
- Direction: Since the coefficient of \( x^2 \) is positive, the parabola opens upwards. If it were negative, the parabola would open downwards.
- Intercepts: The y-intercept of the parabola \( y = x^2 \) is at (0, 0). There are no x-intercepts because the vertex lies on the x-axis.
Here is a step-by-step guide to graphing \( y = x^2 \):
- Plot the Vertex: Start by plotting the vertex at the origin, (0, 0).
- Draw the Axis of Symmetry: Draw a vertical line through the vertex. This line is the axis of symmetry.
- Calculate Additional Points: Choose a few values for \( x \) and calculate the corresponding \( y \) values. For example:
- When \( x = 1 \), \( y = 1^2 = 1 \)
- When \( x = 2 \), \( y = 2^2 = 4 \)
- When \( x = -1 \), \( y = (-1)^2 = 1 \)
- When \( x = -2 \), \( y = (-2)^2 = 4 \)
- Plot the Points: Plot these points on the graph: (1,1), (2,4), (-1,1), and (-2,4).
- Draw the Parabola: Connect the points with a smooth curve, ensuring the curve passes through the vertex and is symmetrical about the y-axis.
The resulting graph is a U-shaped curve that continues infinitely in both the positive and negative directions of the y-axis.
Graphing \( x^2 \) helps in visualizing the behavior of quadratic functions and is a key concept in understanding more complex quadratic equations and their applications.
Common Mistakes and Misconceptions
Understanding x squared is fundamental in algebra, but there are several common mistakes and misconceptions students often encounter. Here, we highlight some of these pitfalls and provide tips to avoid them.
-
Misinterpreting the Square Root:
One common mistake is misunderstanding the square root of x squared. The correct interpretation is \( \sqrt{x^2} = |x| \), which accounts for both positive and negative values of \( x \). Failing to include the absolute value can lead to incorrect solutions.
-
Forgetting to Consider Both Positive and Negative Solutions:
When solving equations like \( x^2 = 4 \), it’s crucial to remember that \( x \) can be both 2 and -2. Omitting one solution can result in incomplete answers.
-
Incorrect Application of the Power Rules:
Another error is misapplying the power rules. For example, \( (x^2)^3 \) should be calculated as \( x^{2 \times 3} = x^6 \). Misapplying these rules leads to incorrect exponents.
-
Sign Errors in Quadratic Equations:
When using the quadratic formula, \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \), it’s essential to correctly handle the plus/minus sign (±) and the entire expression under the square root (discriminant). Sign errors can drastically alter the solution set.
-
Incorrect Distribution:
Students often incorrectly distribute exponents across terms, such as thinking \( (a + b)^2 = a^2 + b^2 \). The correct expansion is \( (a + b)^2 = a^2 + 2ab + b^2 \).
-
Not Simplifying Fully:
Ensure all expressions are fully simplified. For instance, simplify \( x^2 - x^2 = 0 \) rather than leaving it as an unsimplified form.
By being aware of these common mistakes and misconceptions, students can improve their understanding and accuracy when working with x squared and related concepts in algebra.

Advanced Topics: X Squared in Higher Mathematics
The concept of \( x^2 \) extends beyond basic algebra and finds significant applications in various advanced mathematical fields. Here, we explore some of these advanced topics where \( x^2 \) plays a crucial role.
1. Polynomials and Higher-Degree Equations
In higher mathematics, \( x^2 \) is a fundamental building block for polynomials and higher-degree equations. Polynomials are expressions involving sums of powers of \( x \) with coefficients. A general polynomial of degree \( n \) can be written as:
\[
a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0
\]
Here, \( x^2 \) represents the quadratic term. For example, in a cubic polynomial \( x^3 + 2x^2 - x + 1 \), the \( x^2 \) term plays a significant role in the polynomial's behavior.
2. Differential Equations
Differential equations often involve terms with \( x^2 \). For instance, in partial differential equations like the heat equation, the term \( x^2 \) appears as part of the spatial derivatives:
\[
\frac{\partial^2 u}{\partial x^2} = \frac{1}{\alpha} \frac{\partial u}{\partial t}
\]
where \( u(x,t) \) is a function of both space and time, and \( \alpha \) is a constant related to thermal diffusivity.
3. Calculus and Integration
In calculus, \( x^2 \) appears frequently in integration and differentiation. The integral of \( x^2 \) is a basic example:
\[
\int x^2 \, dx = \frac{x^3}{3} + C
\]
where \( C \) is the constant of integration. This principle extends to more complex integrals involving \( x^2 \) and higher powers of \( x \).
4. Series and Sequences
Power series expansions often include \( x^2 \) terms. For example, the Taylor series expansion of a function \( f(x) \) around \( x = 0 \) can be written as:
\[
f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + \cdots
\]
Here, the coefficient of \( x^2 \) is \( \frac{f''(0)}{2!} \), highlighting the importance of \( x^2 \) in series approximations.
5. Complex Numbers and Quadratic Forms
In the study of complex numbers, quadratic forms involve \( x^2 \) and its complex counterpart. A quadratic form in two variables \( x \) and \( y \) is given by:
\[
ax^2 + bxy + cy^2
\]
where \( a \), \( b \), and \( c \) are constants. These forms are essential in understanding the geometry of conic sections and quadratic surfaces.
6. Higher-Dimensional Geometry
In higher-dimensional geometry, \( x^2 \) terms appear in equations defining surfaces and hypersurfaces. For example, the equation of a sphere in three-dimensional space is:
\[
x^2 + y^2 + z^2 = r^2
\]
where \( r \) is the radius. Similarly, \( x^2 \) terms are integral in defining ellipsoids, hyperboloids, and other complex geometric shapes.
7. Eigenvalues and Eigenvectors
In linear algebra, the characteristic equation of a matrix involves \( x^2 \). For a 2x2 matrix \( A \), the characteristic polynomial is:
\[
\det(A - \lambda I) = 0
\]
which expands to a quadratic equation in \( \lambda \), often expressed as:
\[
\lambda^2 - (\text{trace} \, A) \lambda + \det A = 0
\]
This equation's solutions, the eigenvalues, are crucial in understanding the matrix's properties.
These examples illustrate the pervasive presence of \( x^2 \) in advanced mathematical concepts, showcasing its foundational role in both theoretical and applied mathematics.
Frequently Asked Questions
-
What is \( x^2 \)?
\( x^2 \) represents a number \( x \) multiplied by itself. It is read as "x squared".
-
How do you simplify \( x \cdot x^2 \)?
To simplify \( x \cdot x^2 \), you add the exponents: \( x^1 \cdot x^2 = x^{1+2} = x^3 \).
-
What are perfect squares?
Perfect squares are numbers that are the square of an integer. For example, \( 1, 4, 9, 16 \) are perfect squares because they are \( 1^2, 2^2, 3^2, \) and \( 4^2 \) respectively.
-
How do you solve a quadratic equation involving \( x^2 \)?
To solve a quadratic equation of the form \( ax^2 + bx + c = 0 \), you can use the quadratic formula: \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \).
-
What is the graph of \( y = x^2 \) like?
The graph of \( y = x^2 \) is a parabola that opens upwards with its vertex at the origin (0,0).
-
What is the difference between \( x^2 \) and \( 2x \)?
\( x^2 \) is the square of \( x \), while \( 2x \) is \( x \) multiplied by 2. They represent different mathematical operations and yield different results.
-
What is the square root of \( x^2 \)?
The square root of \( x^2 \) is \( x \) if \( x \) is non-negative, and \( |x| \) (the absolute value of \( x \)) in general.
-
How is \( x^2 \) used in physics?
In physics, \( x^2 \) often appears in equations of motion, such as the formula for the displacement of an object under constant acceleration: \( s = ut + \frac{1}{2}at^2 \).
Hướng dẫn chi tiết cách giải phương trình x bình phương = 4 và khám phá các giá trị bình phương khác của x.
Giải phương trình x bình phương = 4 và các giá trị bình phương khác của x
READ MORE:
Khám phá đạo hàm của x bình phương một cách trực quan và dễ hiểu.
Đạo hàm trực quan của x bình phương

x-1=sec(squared)x.jpg)