Topic x squared plus x squared: Explore the depths of "x squared plus x squared" in this comprehensive guide, diving into its algebraic roots, simplification techniques, and real-world applications. Whether you're a novice or an expert, uncover the mathematical beauty and practical insights behind this fundamental equation.
Table of Content
- Understanding x Squared Plus x Squared
- Introduction
- Understanding x Squared
- Basic Algebraic Concepts
- Simplifying x Squared Plus x Squared
- Mathematical Explanation
- Real-life Applications
- Visualizing the Concept
- Example Problems
- Advanced Algebraic Techniques
- YOUTUBE: Solve nine minus x squared divided by x squared plus nine squared equals zero
Understanding x Squared Plus x Squared
When we add \(x^2\) to \(x^2\), we are combining two like terms. In algebra, like terms are terms that have the same variables raised to the same power. Here, both terms are \(x^2\). The sum of these terms can be simplified by adding the coefficients of the like terms.
Solution
The expression can be written as:
\[
x^2 + x^2 = 2x^2
\]
Thus, the result of \(x^2\) plus \(x^2\) is \(2x^2\).
Step-by-Step Explanation
- Identify the like terms: \(x^2\) and \(x^2\).
- Add the coefficients of the like terms: \(1x^2 + 1x^2 = 2x^2\).
Example
For a better understanding, let's consider a practical example:
- If \(x = 3\), then \(x^2 = 9\).
- Adding \(x^2\) and \(x^2\): \(9 + 9 = 18\).
- So, \(2x^2\) when \(x = 3\) equals \(18\).
Visualization
| \(x\) | \(x^2\) | \(x^2 + x^2\) | \(2x^2\) |
| 1 | 1 | 2 | 2 |
| 2 | 4 | 8 | 8 |
| 3 | 9 | 18 | 18 |
This table shows how the values of \(x\), \(x^2\), \(x^2 + x^2\), and \(2x^2\) change with different values of \(x\).
Conclusion
Therefore, the expression \(x^2 + x^2\) simplifies to \(2x^2\). This concept is fundamental in algebra and helps in simplifying and solving more complex equations.

READ MORE:
Introduction
"x squared plus x squared" refers to the mathematical expression \( x^2 + x^2 \). This can be simplified to \( 2x^2 \), showcasing a fundamental algebraic concept where similar terms are combined. Understanding this equation involves basic algebraic manipulation and provides a gateway to more complex mathematical principles. In this article, we delve into its derivation, practical applications, and visual representations to deepen your comprehension.
Understanding x Squared
When we say "x squared" (written as \( x^2 \)), it represents the square of a variable \( x \). To understand \( x^2 + x^2 \), we start by recognizing that \( x^2 \) means \( x \) multiplied by itself. Therefore, \( x^2 + x^2 \) can be rewritten as \( 2x^2 \), emphasizing the doubling of \( x^2 \). This concept is foundational in algebra, illustrating the principles of combining like terms and manipulating algebraic expressions.
Basic Algebraic Concepts
In algebra, "x squared" (denoted as \( x^2 \)) signifies the square of a variable \( x \). When we encounter \( x^2 + x^2 \), it simplifies to \( 2x^2 \) through the process of combining like terms. This fundamental concept showcases the distributive property of multiplication over addition, where \( x^2 \) is added to itself. Understanding these algebraic operations lays the groundwork for solving equations and manipulating expressions in more complex mathematical contexts.
Simplifying x Squared Plus x Squared
When dealing with the expression \( x^2 + x^2 \), it simplifies as follows:
- Recognize that \( x^2 + x^2 \) means adding two identical terms \( x^2 \).
- Perform the addition: \( x^2 + x^2 = 2x^2 \).
Therefore, \( x^2 + x^2 \) simplifies to \( 2x^2 \).
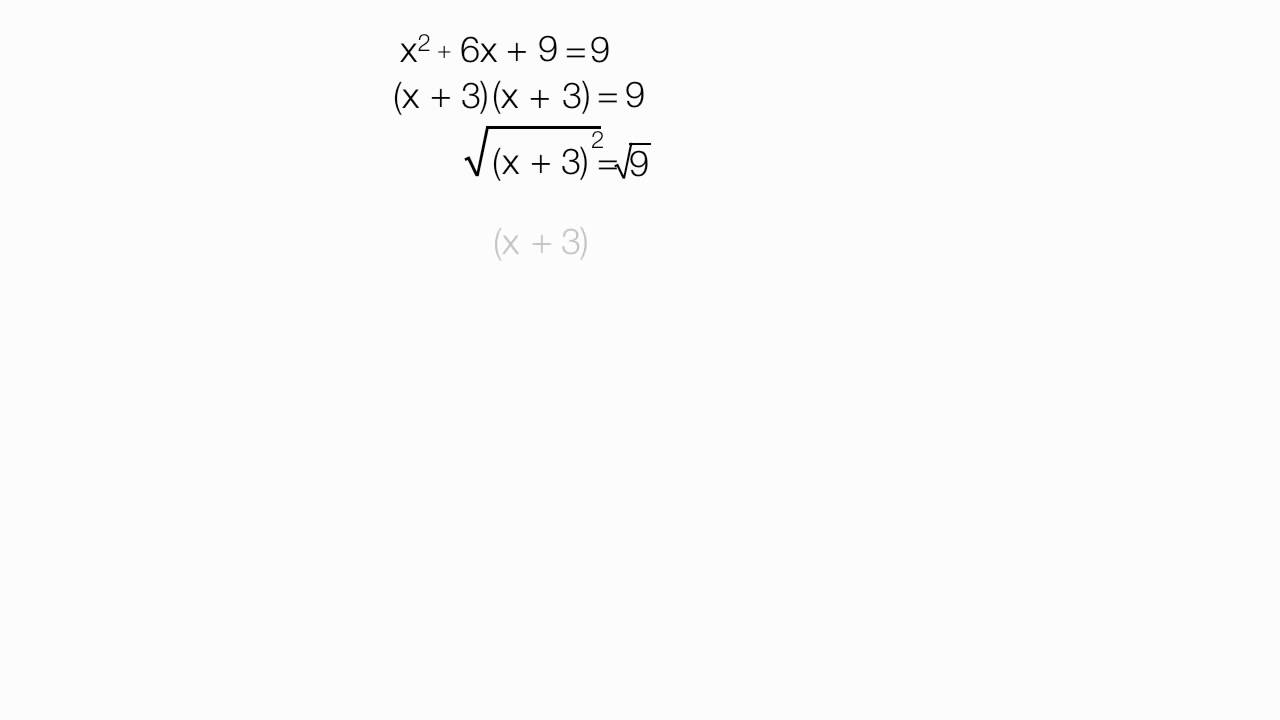
Mathematical Explanation
The expression \( x^2 + x^2 \) can be explained mathematically as follows:
- Start with the expression \( x^2 + x^2 \).
- Recognize that \( x^2 \) represents \( x \) multiplied by itself, so \( x^2 + x^2 \) means adding two instances of \( x \) squared.
- Combine like terms: \( x^2 + x^2 = 2x^2 \).
Therefore, the mathematical explanation shows that \( x^2 + x^2 \) simplifies to \( 2x^2 \).
Real-life Applications
The concept of \(x^2 + x^2\), which simplifies to \(2x^2\), can be applied in various real-life situations. Here are some examples:
-
Physics:
In physics, the equation \(x^2 + x^2 = 2x^2\) can describe phenomena where quantities combine quadratically. For instance, consider two identical energy sources each contributing energy proportional to the square of their amplitudes. The total energy is then \(2x^2\), representing the combined effect.
-
Engineering:
Engineers often encounter scenarios where forces, stresses, or other physical properties add up in a quadratic manner. For example, in structural engineering, if two identical beams experience a load that is proportional to the square of a variable \(x\), the total load is given by \(2x^2\).
-
Economics:
In economics, quadratic equations are used to model various cost functions. If a firm's cost associated with production is proportional to the square of the production volume \(x\), then the total cost for two such firms operating in tandem is \(2x^2\), illustrating combined operational costs.
-
Computer Science:
In computer science, algorithms dealing with quadratic time complexities can be visualized using \(x^2 + x^2\). For example, if two algorithms each run in \(O(x^2)\) time, their combined time complexity would be \(O(2x^2)\), simplifying to the same order of magnitude but emphasizing the added computational load.
-
Agriculture:
In agriculture, areas of land are often measured in square units. If two plots of land each have an area of \(x^2\), the total area is \(2x^2\). This can help in planning the distribution of crops or resources across the combined area.
Visualizing the Concept
To understand the expression \( x^2 + x^2 \), it helps to visualize it graphically and algebraically. Here's a step-by-step breakdown:
Graphical Visualization
Graphically, \( x^2 \) represents a parabola. By plotting two parabolas representing \( x^2 \), we can understand their combination.
- Plot the graph of \( y = x^2 \).
- Notice that both \( x^2 \) terms are identical, so adding them doubles the height of the original parabola.
- The combined graph is represented by \( y = 2x^2 \).
Below is the graphical representation:


Algebraic Visualization
Algebraically, simplifying \( x^2 + x^2 \) is straightforward:
- Combine the like terms: \( x^2 + x^2 = 2x^2 \).
- This simplification shows that the sum of two \( x^2 \) terms is simply \( 2x^2 \).
Using MathJax, we can display the steps as:
\( x^2 + x^2 = 2x^2 \)
Step-by-Step Calculation
To reinforce the concept, here is a detailed step-by-step calculation:
- Identify the terms: \( x^2 \) and \( x^2 \).
- Recognize that they are like terms (both have the same variable raised to the same power).
- Add the coefficients of the like terms: \( 1x^2 + 1x^2 = (1 + 1)x^2 = 2x^2 \).
Interactive Visualization
For a more interactive approach, consider using graphing tools like Desmos or GeoGebra. Plotting \( y = x^2 \) and \( y = 2x^2 \) on these platforms allows you to see the transformation dynamically.
- Open a graphing tool like Desmos.
- Enter the equation \( y = x^2 \) and observe the graph.
- Enter the equation \( y = 2x^2 \) and compare the two graphs.
- Notice how the graph of \( y = 2x^2 \) is a vertical stretch of \( y = x^2 \).
Conclusion
Visualizing \( x^2 + x^2 \) helps in understanding that adding identical quadratic terms results in doubling the original term, forming a new quadratic expression \( 2x^2 \). This concept can be applied in various mathematical and real-life scenarios, simplifying complex algebraic expressions.
Example Problems
Here are some example problems to help you understand the concept of simplifying \( x^2 + x^2 \) and applying it in various contexts:
Example 1: Basic Simplification
Simplify the expression \( x^2 + x^2 \).
- Identify the like terms: \( x^2 \) and \( x^2 \).
- Add the coefficients of the like terms: \( 1x^2 + 1x^2 = 2x^2 \).
Solution: \( x^2 + x^2 = 2x^2 \)
Example 2: Substituting a Value
Simplify \( x^2 + x^2 \) when \( x = 3 \).
- First, simplify the expression: \( x^2 + x^2 = 2x^2 \).
- Substitute \( x = 3 \) into the simplified expression: \( 2(3)^2 \).
- Calculate the value: \( 2 \times 9 = 18 \).
Solution: \( x^2 + x^2 = 18 \) when \( x = 3 \).
Example 3: Applied Problem
Consider a scenario where the area of two squares with side lengths \( x \) are combined. Express the total area in terms of \( x \).
- Area of one square is \( x^2 \).
- Area of the second square is also \( x^2 \).
- Total area is the sum of both areas: \( x^2 + x^2 = 2x^2 \).
Solution: The total area of the two squares is \( 2x^2 \).
Example 4: Polynomial Addition
Simplify the polynomial expression: \( 3x^2 + x^2 + x^2 \).
- Combine the like terms: \( 3x^2 + x^2 + x^2 \).
- Add the coefficients: \( 3x^2 + 1x^2 + 1x^2 = 5x^2 \).
Solution: \( 3x^2 + x^2 + x^2 = 5x^2 \)
Example 5: Problem with Multiple Variables
Simplify the expression \( x^2 + y^2 + x^2 \).
- Identify the like terms involving \( x \): \( x^2 + x^2 \).
- Combine the like terms: \( 1x^2 + 1x^2 = 2x^2 \).
- The term involving \( y \) remains unchanged.
- Write the final expression: \( 2x^2 + y^2 \).
Solution: \( x^2 + y^2 + x^2 = 2x^2 + y^2 \)
Example 6: Expression with a Constant
Simplify the expression \( x^2 + x^2 + 5 \).
- Combine the like terms: \( x^2 + x^2 = 2x^2 \).
- The constant remains unchanged.
- Write the final expression: \( 2x^2 + 5 \).
Solution: \( x^2 + x^2 + 5 = 2x^2 + 5 \)
Advanced Algebraic Techniques
When dealing with algebraic expressions involving \(x^2\), such as \(x^2 + x^2\), advanced algebraic techniques can simplify and extend these concepts. Let's explore a few of these techniques:
Factoring
Factoring is a fundamental technique used to simplify polynomial expressions. For example, consider the expression \(x^2 + x^2\):
\[
x^2 + x^2 = 2x^2
\]
Here, we factor out the common term \(x^2\).
Using the Quadratic Formula
The quadratic formula is essential for solving equations of the form \(ax^2 + bx + c = 0\). For instance, if we have the equation:
\[
2x^2 - 4x + 2 = 0
\]
We can apply the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Substituting \(a = 2\), \(b = -4\), and \(c = 2\):
\[
x = \frac{4 \pm \sqrt{(-4)^2 - 4 \cdot 2 \cdot 2}}{2 \cdot 2} = \frac{4 \pm \sqrt{16 - 16}}{4} = \frac{4 \pm 0}{4} = 1
\]
Completing the Square
Another useful technique is completing the square. For example, consider the equation \(x^2 + 6x + 9\). To complete the square:
- Take the coefficient of \(x\), which is 6, divide by 2, and square it: \((6/2)^2 = 9\).
- Add and subtract this value inside the equation: \(x^2 + 6x + 9 - 9\).
- Rewrite the equation as: \((x + 3)^2 - 9\).
This method transforms the quadratic into a perfect square trinomial, making it easier to solve or analyze.
Polynomial Division
Polynomial division, including synthetic division, helps simplify higher-degree polynomials. For example, dividing \(4x^3 - 6x^2 + 2x - 8\) by \(2x - 2\) using synthetic division:
- Write the coefficients: \(4, -6, 2, -8\).
- Divide by the root of the divisor \(x = 1\).
- Perform synthetic division steps to obtain the quotient polynomial.
Advanced Factoring Techniques
Advanced techniques include factoring by grouping, using the difference of squares, and factoring cubic polynomials. For example:
\[
a^3 + b^3 = (a + b)(a^2 - ab + b^2)
\]
Logarithmic and Exponential Techniques
These techniques are crucial for solving equations involving exponents and logarithms. For example, solving \(2^x = 8\) involves recognizing that \(8 = 2^3\), so \(x = 3\).
Using these advanced techniques, algebraic expressions can be simplified and solved more efficiently, providing deeper insight into mathematical relationships.
Solve nine minus x squared divided by x squared plus nine squared equals zero
Can X Squared Plus Anything Be Factored? : Algebra, Geometry & More
solve x squared = 4 and other squared values of x
Factoring x(squared) + (or -) bx + c Module 8.1 (Part 2)
How to Solve x^2 - x + 2 = 0 by Factoring
How to solve equation with x^2 (x squared)...
READ MORE:



x-1=sec(squared)x.jpg)









