Topic tan x squared: The concept of "tan x squared" plays a crucial role in trigonometry, involving the identity \(\tan^2{x} = \sec^2{x} - 1\). This identity is essential for simplifying trigonometric expressions and solving equations. This article will delve into its mathematical significance, practical applications, and provide examples to enhance your understanding.
Table of Content
Understanding the Tangent Squared Function
The tangent squared function, denoted as \( \tan^2{x} \), is a significant concept in trigonometry. This function is widely used in various mathematical calculations, particularly in integration and solving trigonometric equations.
Formula
The formula for the square of the tangent function is given by:
\[ \tan^2{\theta} = \sec^2{\theta} - 1 \]
This formula is derived from the Pythagorean identity involving tangent and secant functions.
Integration of \( \tan^2{x} \)
The integration of the tangent squared function can be expressed as:
\[ \int \tan^2{x} \, dx = \int (\sec^2{x} - 1) \, dx \]
Breaking it down, we get:
\[ \int \sec^2{x} \, dx - \int 1 \, dx \]
Which simplifies to:
\[ \tan{x} - x + C \]
Therefore, the integral of \( \tan^2{x} \) is \( \tan{x} - x + C \), where \( C \) is the constant of integration.
Example Calculation
Let's calculate the definite integral of \( \tan^2{x} \) from 0 to \( \frac{\pi}{4} \):
\[ \int_{0}^{\frac{\pi}{4}} \tan^2{x} \, dx = \left[ \tan{x} - x + C \right]_{0}^{\frac{\pi}{4}} \]
Evaluating the limits, we get:
\[ \tan{\frac{\pi}{4}} - \frac{\pi}{4} + C - \left( \tan{0} - 0 + C \right) = 1 - \frac{\pi}{4} \]
Applications
The tangent squared function is useful in various fields including engineering, physics, and higher mathematics. Understanding its properties and applications can provide deeper insights into complex trigonometric and calculus problems.
Important Notes
- The formula for the integration of \( \tan^2{x} \) is \( \tan{x} - x + C \).
- The tangent squared function identity can simplify the calculation of integrals involving trigonometric functions.
- Definite integrals of \( \tan^2{x} \) can be evaluated using the limits and the formula.
x-1=sec(squared)x.jpg)
READ MORE:
Introduction to Tan X Squared
The expression , often written as or , involves the tangent function raised to the power of two. This distinction is crucial as refers to the tangent of squared, whereas indicates squaring the tangent of . Understanding these differences is vital for solving various trigonometric problems, particularly in integration and differentiation.
The tangent function, a fundamental trigonometric function, is defined as the ratio of the sine and cosine functions. Therefore, we can express the square of the tangent function as:
This representation is useful when simplifying complex trigonometric expressions or when integrating functions involving . The integral of is given by:
This formula is derived using the identity and is instrumental in solving definite integrals. For instance, the definite integral from 0 to is:
Such integrations are essential in various fields of science and engineering. Additionally, the concept extends to more complex integrals, such as , which can be solved by substitution, yielding:
In summary, understanding and its properties is crucial for solving advanced trigonometric problems and applications.
Formula and Identity
When working with trigonometric functions, understanding their various identities and formulas is crucial. The tangent squared function, denoted as \( \tan^2(x) \), has several important identities and properties that can simplify complex expressions and integrals.
The primary identity involving \( \tan^2(x) \) is derived from the Pythagorean identity:
\(1 + \tan^2(x) = \sec^2(x)\)
This identity can be rearranged to solve for \( \tan^2(x) \):
\( \tan^2(x) = \sec^2(x) - 1 \)
This relationship is frequently used in calculus, particularly in integration and differentiation of trigonometric functions. Here are some steps and examples:
Integration of \( \tan^2(x) \)
The integral of \( \tan^2(x) \) can be found by using the identity:
\(\int \tan^2(x) \, dx = \int (\sec^2(x) - 1) \, dx\)
Splitting the integral:
\(= \int \sec^2(x) \, dx - \int 1 \, dx\)
Solving these integrals:
\(= \tan(x) - x + C\)
Thus, the integral of \( \tan^2(x) \) is:
\(\int \tan^2(x) \, dx = \tan(x) - x + C\)
Example: Integration from 0 to \( \frac{\pi}{4} \)
To find the definite integral of \( \tan^2(x) \) from 0 to \( \frac{\pi}{4} \), we use the result of the indefinite integral:
\(\int_{0}^{\frac{\pi}{4}} \tan^2(x) \, dx = \left[ \tan(x) - x \right]_{0}^{\frac{\pi}{4}}\)
Evaluating at the bounds:
\(\left( \tan \left( \frac{\pi}{4} \right) - \frac{\pi}{4} \right) - \left( \tan(0) - 0 \right)\)
\(= 1 - \frac{\pi}{4}\)
Thus, the definite integral is:
\(\int_{0}^{\frac{\pi}{4}} \tan^2(x) \, dx = 1 - \frac{\pi}{4}\)
These identities and calculations are essential tools in trigonometry and calculus, aiding in the simplification and evaluation of complex expressions.
Integration of Tan Squared X
The integral of \(\tan^2 x\) is a common problem in calculus. To integrate \(\tan^2 x\), we can use trigonometric identities and fundamental integration techniques. The standard result is:
\[
\int \tan^2 x \, dx = \tan x - x + C
\]
where \(C\) is the constant of integration.
Here are the steps involved:
- Use the identity \(\sec^2 x = 1 + \tan^2 x\).
- Rearrange it to \(\tan^2 x = \sec^2 x - 1\).
- Substitute into the integral: \(\int \tan^2 x \, dx = \int (\sec^2 x - 1) \, dx\).
- Separate the integrals: \(\int \sec^2 x \, dx - \int 1 \, dx\).
- Integrate each term: \(\int \sec^2 x \, dx = \tan x\) and \(\int 1 \, dx = x\).
- Combine the results: \(\int \tan^2 x \, dx = \tan x - x + C\).
This result can also be verified by using methods such as integration by parts, substitution, and definite integrals over specific intervals.
Derivative of Tan Squared X
The derivative of the function \( \tan^2(x) \) involves using the chain rule and the product rule. To understand how to derive this function, let's break it down step-by-step.
Formula and Step-by-Step Calculation
To find the derivative of \( \tan^2(x) \), we start by applying the chain rule. The chain rule states that the derivative of a composite function is the derivative of the outer function multiplied by the derivative of the inner function.
- Let \( u = \tan(x) \). Then \( \tan^2(x) = (u)^2 \).
- Differentiate \( (u)^2 \) with respect to \( u \):
\[ \frac{d}{du}(u^2) = 2u \] - Now, differentiate \( u = \tan(x) \) with respect to \( x \):
\[ \frac{d}{dx}(\tan(x)) = \sec^2(x) \] - Combine these results using the chain rule:
\[ \frac{d}{dx}(\tan^2(x)) = 2 \tan(x) \cdot \sec^2(x) \]
Verification Using Product Rule
The derivative can also be verified using the product rule. The product rule states that the derivative of the product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
- Express \( \tan^2(x) \) as \( \tan(x) \cdot \tan(x) \).
- Apply the product rule:
\[ \frac{d}{dx}(\tan(x) \cdot \tan(x)) = \tan(x) \cdot \frac{d}{dx}(\tan(x)) + \frac{d}{dx}(\tan(x)) \cdot \tan(x) \] - Simplify the expression:
\[ \tan(x) \cdot \sec^2(x) + \sec^2(x) \cdot \tan(x) = 2 \tan(x) \cdot \sec^2(x) \]
Conclusion
Thus, the derivative of \( \tan^2(x) \) is:
\[
\frac{d}{dx}(\tan^2(x)) = 2 \tan(x) \sec^2(x)
\]
This result can be obtained through both the chain rule and the product rule, ensuring its correctness and demonstrating different methods for approaching the differentiation of composite trigonometric functions.

Proof and Examples
The function \( \tan^2(x) \) can be analyzed and proven using trigonometric identities and calculus principles. Here, we will explore a step-by-step proof and provide examples to illustrate the concepts.
Proof of \( \tan^2(x) \) Using Trigonometric Identities
- Start with the Pythagorean identity: \[ \sin^2(x) + \cos^2(x) = 1 \]
- Divide the entire equation by \( \cos^2(x) \): \[ \frac{\sin^2(x)}{\cos^2(x)} + \frac{\cos^2(x)}{\cos^2(x)} = \frac{1}{\cos^2(x)} \]
- Simplify using the definitions of \( \tan(x) \) and \( \sec(x) \): \[ \tan^2(x) + 1 = \sec^2(x) \]
Examples
Here are a few examples to demonstrate the application of the trigonometric identity and calculus:
-
Example 1: Simplify \( \tan^2(x) \)
Given the identity \( \tan^2(x) = \sec^2(x) - 1 \), simplify \( \tan^2(45^\circ) \):
\[ \tan^2(45^\circ) = \sec^2(45^\circ) - 1 \]
Since \( \sec(45^\circ) = \sqrt{2} \):
\[ \tan^2(45^\circ) = (\sqrt{2})^2 - 1 = 2 - 1 = 1 \] -
Example 2: Integration of \( \tan^2(x) \)
To integrate \( \tan^2(x) \), use the identity:
\[ \int \tan^2(x) \, dx = \int (\sec^2(x) - 1) \, dx \]
This can be split into two integrals:
\[ \int \sec^2(x) \, dx - \int 1 \, dx = \tan(x) - x + C \]
where \( C \) is the constant of integration. -
Example 3: Derivative of \( \tan^2(x) \)
The derivative of \( \tan^2(x) \) can be found using the chain rule:
\[ \frac{d}{dx} [\tan^2(x)] = 2 \tan(x) \cdot \sec^2(x) \]
Conclusion
By understanding the proofs and working through examples, one can gain a deeper comprehension of \( \tan^2(x) \) and its applications in calculus and trigonometry.
Applications in Calculus
The function \( \tan^2(x) \) finds various applications in calculus, particularly in the evaluation of integrals and derivatives. This section explores several key applications, including integration techniques, differentiation methods, and practical examples.
1. Integration of \( \tan^2(x) \)
To integrate \( \tan^2(x) \), we use the identity:
\[
\tan^2(x) = \sec^2(x) - 1
\]
Thus, the integral of \( \tan^2(x) \) can be written as:
\[
\int \tan^2(x) \, dx = \int (\sec^2(x) - 1) \, dx
\]
This simplifies to:
\[
\int \tan^2(x) \, dx = \int \sec^2(x) \, dx - \int 1 \, dx
\]
Which results in:
\[
\int \tan^2(x) \, dx = \tan(x) - x + C
\]
where \( C \) is the constant of integration.
2. Derivative of \( \tan^2(x) \)
To find the derivative of \( \tan^2(x) \), we apply the chain rule:
\[
\frac{d}{dx}[\tan^2(x)] = 2 \tan(x) \cdot \frac{d}{dx}[\tan(x)]
\]
Knowing that:
\[
\frac{d}{dx}[\tan(x)] = \sec^2(x)
\]
We get:
\[
\frac{d}{dx}[\tan^2(x)] = 2 \tan(x) \cdot \sec^2(x)
\]
3. Practical Examples
Let's consider some examples to illustrate these concepts.
Example 1: Evaluating an Integral
Evaluate the integral:
\[
\int_0^{\frac{\pi}{4}} \tan^2(x) \, dx
\]
Using the identity \( \tan^2(x) = \sec^2(x) - 1 \), we have:
\[
\int_0^{\frac{\pi}{4}} \tan^2(x) \, dx = \int_0^{\frac{\pi}{4}} (\sec^2(x) - 1) \, dx
\]
This can be split into two integrals:
\[
\int_0^{\frac{\pi}{4}} \sec^2(x) \, dx - \int_0^{\frac{\pi}{4}} 1 \, dx
\]
We know that:
\[
\int_0^{\frac{\pi}{4}} \sec^2(x) \, dx = \tan(x) \bigg|_0^{\frac{\pi}{4}} = 1 - 0 = 1
\]
And:
\[
\int_0^{\frac{\pi}{4}} 1 \, dx = x \bigg|_0^{\frac{\pi}{4}} = \frac{\pi}{4} - 0 = \frac{\pi}{4}
\]
Therefore:
\[
\int_0^{\frac{\pi}{4}} \tan^2(x) \, dx = 1 - \frac{\pi}{4}
\]
Example 2: Finding a Derivative
Find the derivative of \( f(x) = \tan^2(3x) \).
Using the chain rule and the derivative of \( \tan^2(x) \), we get:
\[
\frac{d}{dx}[\tan^2(3x)] = 2 \tan(3x) \cdot \frac{d}{dx}[\tan(3x)]
\]
Since:
\[
\frac{d}{dx}[\tan(3x)] = 3 \sec^2(3x)
\]
We have:
\[
\frac{d}{dx}[\tan^2(3x)] = 2 \tan(3x) \cdot 3 \sec^2(3x) = 6 \tan(3x) \sec^2(3x)
\]
4. Practical Applications
The function \( \tan^2(x) \) and its derivatives are often used in solving problems involving trigonometric integrals and differential equations. For instance, it appears in calculating the area under a curve in trigonometric integrals and in the analysis of periodic functions.
Graphical Representation
The graphical representation of the function \( \tan^2(x) \) and its derivative provides insight into their behaviors and characteristics.
1. Plotting \( \tan^2(x) \):
To graph \( \tan^2(x) \), note the following key points:
- The function \( \tan(x) \) has vertical asymptotes at \( x = \frac{\pi}{2} + k\pi \), where \( k \) is an integer. These asymptotes will also appear in the graph of \( \tan^2(x) \).
- The function \( \tan^2(x) \) is always non-negative and tends to infinity near its asymptotes.
- The function has periodicity of \( \pi \), repeating its pattern every \( \pi \) units.
Below is a table with some key values:
| x | \( \tan(x) \) | \( \tan^2(x) \) |
|---|---|---|
| 0 | 0 | 0 |
| \( \frac{\pi}{4} \) | 1 | 1 |
| \( \frac{\pi}{2} \) | undefined | undefined |
2. Derivative of \( \tan^2(x) \):
The derivative of \( \tan^2(x) \) can be found using the chain rule:
\[
\frac{d}{dx} [\tan^2(x)] = 2 \tan(x) \cdot \sec^2(x)
\]
The graph of the derivative \( 2 \tan(x) \cdot \sec^2(x) \) exhibits the following properties:
- It has the same vertical asymptotes as \( \tan^2(x) \).
- It oscillates between positive and negative values, reflecting the periodic and alternating nature of \( \tan(x) \).
3. Graphical Visualization:
Using tools like Desmos, we can visualize the functions and their derivatives effectively. Below are examples of how the functions appear:
The visualization shows the key features of the functions, including their periodicity, asymptotic behavior, and oscillations. By analyzing these graphs, one gains a deeper understanding of the mathematical properties and applications of \( \tan^2(x) \) and its derivative.
Frequently Asked Questions
Here are some common questions and answers related to the integration and differentiation of tan squared x.
-
What is the formula for tan squared x?
The formula for tan squared x is:
\[ \tan^2{x} = \sec^2{x} - 1 \] -
How do you integrate tan squared x?
To integrate tan squared x, we use the identity:
\[ \int \tan^2{x} \, dx = \int (\sec^2{x} - 1) \, dx \]
This can be further simplified to:
\[ \int \sec^2{x} \, dx - \int 1 \, dx \]
Which gives:
\[ \tan{x} - x + C \]
where \( C \) is the constant of integration. -
What is the derivative of tan squared x?
The derivative of tan squared x is found using the chain rule:
\[ \frac{d}{dx} [\tan^2{x}] = 2 \tan{x} \cdot \sec^2{x} \] -
How do you prove the identity \(\tan^2{x} = \sec^2{x} - 1\)?
Starting from the Pythagorean identity:
\[ \sec^2{x} = 1 + \tan^2{x} \]
Subtract 1 from both sides to get:
\[ \tan^2{x} = \sec^2{x} - 1 \] -
What is the graphical representation of tan squared x?
The graph of tan squared x is derived from the graph of tan x, squared. Key points include:
- It has vertical asymptotes at \( x = \frac{\pi}{2} + n\pi \) for any integer \( n \).
- It is always positive as the square of any real number is non-negative.
- The function has a minimum value of 0 at \( x = n\pi \) for any integer \( n \).
-
In which calculus problems is tan squared x commonly used?Tan squared x is frequently encountered in problems involving trigonometric integrals and derivatives, particularly in the context of solving integrals and applying trigonometric identities to simplify expressions. It is also used in problems involving the Pythagorean identities and solving trigonometric equations.
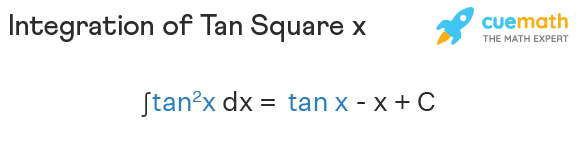
Hướng dẫn tích phân sử dụng t=tan(x/2) - [Phép thế Weierstrass]