Topic x squared divided by x: Understanding how to simplify expressions like x squared divided by x is fundamental in algebra. This article delves into the principles of polynomial division, common mistakes, and practical applications. Whether you're a student or a math enthusiast, you'll find valuable insights and tips to enhance your mathematical skills.
Table of Content
- Understanding \( \frac{x^2}{x} \)
- Introduction to Basic Algebra
- Simplifying Expressions
- Understanding Polynomial Division
- Common Mistakes in Division
- Applications in Real-World Problems
- Visual Aids and Graphical Representation
- Practice Problems and Solutions
- Advanced Division Techniques
- Frequently Asked Questions
- Additional Resources for Further Learning
- YOUTUBE: Giải bài toán: Giải phương trình chín trừ x bình phương chia cho x bình phương cộng chín bình phương bằng không. Xem video để hiểu rõ hơn.
Understanding \( \frac{x^2}{x} \)
The expression \( \frac{x^2}{x} \) simplifies to \( x \) for all values of \( x \) except \( x = 0 \). This is because:
\[
\frac{x^2}{x} = x^{2-1} = x
\]
Examples and Applications
-
Simplifying Algebraic Expressions:
When dividing \( x^2 \) by \( x \), the result is \( x \). This is useful in simplifying algebraic expressions and solving equations.
-
Polynomial Division:
In polynomial division, dividing \( x^2 \) by \( x \) is a common step that simplifies the polynomial to a lower degree.
-
Real-World Applications:
Understanding how to simplify \( \frac{x^2}{x} \) can be applied in various real-world problems involving rates, areas, and more.
Practice Problems
-
Divide \( x^3 \) by \( x \).
\[
\frac{x^3}{x} = x^{3-1} = x^2
\] -
Divide \( x^4 \) by \( x^2 \).
\[
\frac{x^4}{x^2} = x^{4-2} = x^2
\] -
Simplify \( \frac{x^5}{x^3} \).
\[
\frac{x^5}{x^3} = x^{5-3} = x^2
\]
Visual Representation
Below is a table representing different values of \( x \) and the result of \( \frac{x^2}{x} \).
| \( x \) | \( \frac{x^2}{x} \) |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |

READ MORE:
Introduction to Basic Algebra
Basic algebra is a fundamental branch of mathematics that deals with variables, expressions, and equations. It provides the tools to solve problems and understand relationships between quantities. One of the key concepts in algebra is simplifying expressions.
In algebra, variables such as x are used to represent unknown values. Expressions combine these variables with numbers and operations like addition, subtraction, multiplication, and division.
Let's start by understanding how to simplify an expression involving x. Consider the expression:
\[ \frac{x^2}{x} \]
To simplify this expression, follow these steps:
- Identify the common factors: In the numerator, we have \(x^2\), which means \(x \times x\). In the denominator, we have \(x\).
- Cancel the common factors: Since \(x\) is a common factor in both the numerator and the denominator, we can cancel it out: \[ \frac{x \times x}{x} = x \]
- Result: The simplified form of \(\frac{x^2}{x}\) is \(x\).
It's essential to understand why this simplification works. Division in algebra is similar to division in arithmetic. When you divide \(x^2\) by \(x\), you are essentially dividing two quantities that have the same base. The rules of exponents tell us that:
\[ \frac{x^a}{x^b} = x^{a-b} \]
Applying this rule to our example:
\[ \frac{x^2}{x} = x^{2-1} = x^1 = x \]
This simplification process is a crucial skill in algebra as it helps in solving equations and understanding more complex mathematical concepts.
Here is a table summarizing the rules of exponents:
| Expression | Simplified Form |
|---|---|
| \( \frac{x^a}{x^b} \) | \( x^{a-b} \) |
| \( x^a \times x^b \) | \( x^{a+b} \) |
| \( (x^a)^b \) | \( x^{a \times b} \) |
Mastering these rules will enable you to tackle a wide range of algebraic problems. In the next sections, we will delve deeper into simplifying expressions, understanding polynomial division, and exploring more advanced algebraic techniques.
Simplifying Expressions
In algebra, simplifying expressions is a crucial skill. It involves reducing expressions to their simplest form to make them easier to work with. Let's explore the simplification process using the expression \( \frac{x^2}{x} \).
To simplify \( \frac{x^2}{x} \):
- First, recognize that \( x^2 \) can be written as \( x \times x \).
- Therefore, \( \frac{x^2}{x} \) becomes \( \frac{x \times x}{x} \).
- Next, cancel the common factor of \( x \) in the numerator and the denominator.
- After canceling, you are left with \( x \).
So, \( \frac{x^2}{x} = x \).
Let's look at a few more examples:
- Example 1: Simplify \( \frac{y^3}{y} \)
- Rewrite as \( \frac{y \times y \times y}{y} \)
- Cancel the common factor of \( y \)
- The result is \( y^2 \)
- Example 2: Simplify \( \frac{z^4}{z^2} \)
- Rewrite as \( \frac{z \times z \times z \times z}{z \times z} \)
- Cancel the common factors of \( z \times z \)
- The result is \( z^2 \)
When simplifying expressions with exponents, remember these key rules:
- Product of Powers: \( x^a \times x^b = x^{a+b} \)
- Quotient of Powers: \( \frac{x^a}{x^b} = x^{a-b} \)
- Power of a Power: \( (x^a)^b = x^{a \times b} \)
By understanding and applying these rules, you can simplify even complex algebraic expressions efficiently.
Understanding Polynomial Division
Polynomial division is a fundamental concept in algebra that involves dividing a polynomial by another polynomial. There are two primary methods for dividing polynomials: long division and synthetic division. In this section, we will focus on long division.
Steps for Polynomial Long Division
-
Arrange the Polynomials: Ensure both the dividend (the polynomial to be divided) and the divisor are written in descending order of their degrees. For example, if you are dividing \(2x^3 - 2x^2 + 3x - 3\) by \(x - 1\), both should be arranged with the highest power first.
-
Divide the Leading Terms: Divide the leading term of the dividend by the leading term of the divisor. In our example, \(\frac{2x^3}{x} = 2x^2\). Write this result above the division line.
-
Multiply and Subtract: Multiply the entire divisor by the term just found (in this case, \(2x^2\)) and subtract this from the dividend. This step reduces the degree of the polynomial. For instance:
\[
(2x^3 - 2x^2 + 3x - 3) - (2x^2 \cdot (x - 1)) = 2x^3 - 2x^2 + 3x - 3 - (2x^3 - 2x^2) = 3x - 3.
\] -
Repeat the Process: Treat the result from the subtraction as the new dividend and repeat the division process until the degree of the remainder is less than the degree of the divisor. Continuing with our example:
\[
\frac{3x}{x} = 3,
\]
\[
(3x - 3) - (3 \cdot (x - 1)) = 3x - 3 - 3x + 3 = 0.
\] -
Write the Final Quotient and Remainder: The terms above the division line give the quotient. If there's no remainder, the division is exact. For our example, the final quotient is \(2x^2 + 3\) with a remainder of 0.
Example
Consider the division problem: \(\frac{2x^3 - 2x^2 + 3x - 3}{x - 1}\).
|
Thus, the quotient is \(2x^2 + 3\) with a remainder of 0.
Synthetic Division
Synthetic division is another method used to divide polynomials, but it is applicable only when dividing by a linear binomial of the form \(x - k\). This method simplifies the process by using only the coefficients of the polynomials.
Steps for Synthetic Division
- Write the coefficients of the dividend in descending order. Use 0 for any missing terms.
- Write the value of \(k\) (from \(x - k\)) on the left.
- Bring down the leading coefficient to the bottom row.
- Multiply this leading coefficient by \(k\) and write the result under the next coefficient.
- Add the numbers in the second column and write the result in the bottom row.
- Repeat the multiplication and addition steps until all coefficients are processed.
- The bottom row gives the coefficients of the quotient, and the final number is the remainder.
For example, dividing \(x^2 + 3\) by \(x - 4\) using synthetic division:
| \(4 \quad | \quad 1 \quad 0 \quad 3\) |
| \(\downarrow\) |
| \( \quad | \quad 1 \quad 4 \quad 19\) |
| \(\downarrow\) |
| \(\quad \quad 1 \quad 4 \quad 19\) |
The quotient is \(x + 4\) and the remainder is 19.
Both methods of polynomial division are essential tools in algebra, allowing for the simplification and solution of complex polynomial expressions.
Common Mistakes in Division
When dividing expressions, especially polynomials, there are several common mistakes that students often make. Recognizing these errors can help in avoiding them and understanding the correct methods of division.
- Incorrect Cancellation: One frequent mistake is improperly canceling terms. For instance, when simplifying
$$\frac{x^2}{x}$$ , some might incorrectly cancel the x's without considering the exponents properly. The correct simplification is$$x$$ because$$x^2 \div x = x^{2-1} = x$$ . - Misunderstanding the Division Algorithm: The polynomial division algorithm states that for polynomials \(f(x)\) and \(g(x)\), there exist unique polynomials \(q(x)\) and \(r(x)\) such that:
$$f(x) = g(x)q(x) + r(x)$$ where the degree of \(r(x)\) is less than the degree of \(g(x)\). A common mistake is not correctly identifying \(q(x)\) and \(r(x)\), leading to incorrect results.
- Ignoring Remainders: When dividing polynomials, it is crucial to consider the remainder. For example, dividing \(2x^2 - 5x - 1\) by \(x - 3\) correctly, we get:
$$2x^2 - 5x - 1 = (x - 3)(2x + 1) + 2$$ where 2 is the remainder. Ignoring this remainder is a common error.
- Incorrectly Applying the Remainder Theorem: The Remainder Theorem states that for a polynomial \(f(x)\), the remainder of the division by \(x - c\) is \(f(c)\). A mistake here is either not applying the theorem correctly or misunderstanding that the remainder must be a constant when dividing by a linear polynomial.
- Errors in Synthetic Division: Synthetic division is a shortcut method for polynomial division when dividing by a linear factor. Errors in setting up or performing synthetic division can lead to incorrect quotients and remainders. For example, dividing \(x^2 + 2x + 6\) by \(x - 1\) using synthetic division requires careful alignment and correct arithmetic operations.
- Sign Errors: Sign errors frequently occur during the division process. For example, when dividing a polynomial by a binomial with a negative coefficient, it is important to distribute the negative sign correctly throughout the process.
By being aware of these common mistakes, students can better approach polynomial division and ensure accurate results.
Applications in Real-World Problems
Understanding the concept of polynomial division, such as dividing \( x^2 \) by \( x \), is essential in solving a variety of real-world problems. Here, we will explore some practical applications where polynomial division plays a crucial role.
1. Physics: Motion and Trajectories
Polynomial equations often describe the motion of objects. For instance, the trajectory of a projectile can be modeled using a quadratic equation:
\[ h(t) = -\frac{1}{2}gt^2 + v_0t + h_0 \]
where:
- \( g \) is the acceleration due to gravity
- \( v_0 \) is the initial velocity
- \( h_0 \) is the initial height
By dividing and simplifying these polynomial expressions, we can determine the time of flight, maximum height, and range of the projectile.
2. Economics: Cost and Revenue Analysis
In economics, polynomial division is used to model and analyze cost and revenue functions. For example, if the revenue \( R(x) \) and cost \( C(x) \) of producing \( x \) units of a product are given by polynomials, the profit \( P(x) \) can be found by:
\[ P(x) = R(x) - C(x) \]
Simplifying these expressions helps businesses determine the optimal production levels and pricing strategies to maximize profit.
3. Engineering: Structural Analysis
Engineers use polynomial division to analyze and design structures. For instance, the bending of beams under load can be modeled using polynomial equations. By dividing these polynomials, engineers can determine stress, strain, and deflection in the materials, ensuring safety and efficiency in construction.
4. Environmental Science: Population Modeling
Population growth and decay can also be described using polynomial equations. For example, the growth of a bacterial population might be modeled by a polynomial function of time. By dividing and simplifying these functions, scientists can predict future population sizes and understand the factors influencing growth rates.
5. Computer Graphics: Curve Fitting
In computer graphics, polynomial division is used for curve fitting and interpolation. By dividing polynomials, graphic designers can create smooth curves and surfaces that accurately represent complex shapes. This technique is crucial in animation, CAD (Computer-Aided Design), and other graphical applications.
These examples illustrate the importance of understanding polynomial division and its applications in various fields. Mastering these concepts not only helps in academic pursuits but also in solving real-world problems effectively.
Visual Aids and Graphical Representation
Visual aids and graphical representation are powerful tools to understand mathematical concepts such as . They provide a clear and intuitive way to see how expressions and equations behave. Below are some common methods used for graphical representation:
- Line Graphs: Used to display continuous data and are useful for predicting trends over time.
- Bar Graphs: Display categorical data and compare quantities using solid bars.
- Histograms: Represent the frequency of numerical data organized into intervals, showing data distribution.
- Scatter Plots: Show relationships between two variables, often revealing correlations.
For example, to visualize the expression , we can use a coordinate system:
- Plotting the Function: Consider the function . Simplifying this gives . We can plot this function on a graph with the x-axis representing the input values and the y-axis representing the output values.
- Using Desmos: Tools like Desmos can be extremely helpful. By inputting
y = xinto Desmos, we can see a straight line passing through the origin with a slope of 1, visually confirming the relationship. - Graphical Analysis: Observing the graph, we can identify key features such as intercepts, slopes, and how the function behaves as x increases or decreases.
Here is an example using Desmos to visualize :
In the graph above, you can see how the line y = x demonstrates the simplified form of the expression . This visual representation aids in understanding the division of polynomials and reinforces the concept that simplifies to .
Practice Problems and Solutions
Here are some practice problems and their solutions related to dividing \( x^2 \) by \( x \):
- Simplify the expression \( \frac{x^2}{x} \).
- Determine the value of \( x \) if \( \frac{x^2}{x} = 5 \).
- Solve the inequality \( \frac{x^2}{x} < 4 \).
| Step 1: | Identify the expression \( \frac{x^2}{x} \). |
| Step 2: | Apply the division property of exponents: \( \frac{x^2}{x} = x^{2-1} = x \). |
Solution: \( \frac{x^2}{x} = x \).
| Step 1: | Set up the equation \( \frac{x^2}{x} = 5 \). |
| Step 2: | Solve for \( x \): \( x^2 = 5x \). |
| Step 3: | Factor out \( x \): \( x(x - 5) = 0 \). |
| Step 4: | Find solutions: \( x = 0 \) or \( x = 5 \). |
Solutions: \( x = 0 \) or \( x = 5 \).
| Step 1: | Set up the inequality \( \frac{x^2}{x} < 4 \). |
| Step 2: | Simplify: \( x < 4 \) (note: \( x \neq 0 \)). |
Solution: \( x < 4 \) (where \( x \neq 0 \)).
Advanced Division Techniques
Explore advanced techniques for dividing \( x^2 \) by \( x \):
- Factor and simplify expressions involving \( x^2 \) divided by \( x \).
- Consider cases where \( x \) might equal 0 and implications for the division.
- Apply division techniques in more complex algebraic contexts.
| Step 1: | Factor out \( x \) from \( x^2 \): \( \frac{x^2}{x} = x \). |
| Step 2: | Apply the division property of exponents: \( x^{2-1} = x \). |
Result: \( \frac{x^2}{x} = x \).
| Step 1: | Discuss the scenario when \( x = 0 \). |
| Step 2: | Understand that \( \frac{x^2}{x} \) is undefined when \( x = 0 \). |
Note: \( \frac{x^2}{x} \) is undefined at \( x = 0 \).
| Step 1: | Extend the concept to higher-order polynomials. |
| Step 2: | Utilize polynomial long division if necessary. |
Example: Divide \( x^3 + 2x^2 - 3x \) by \( x \).

Frequently Asked Questions
Answers to common questions about dividing \( x^2 \) by \( x \):
- What is \( \frac{x^2}{x} \)?
- Why is \( \frac{x^2}{x} \) undefined when \( x = 0 \)?
- Can \( \frac{x^2}{x} \) be simplified further?
| Answer: | \( \frac{x^2}{x} \) simplifies to \( x \), utilizing the division property of exponents. |
| Answer: | Division by zero is undefined in mathematics, hence \( \frac{x^2}{x} \) is not defined at \( x = 0 \). |
| Answer: | \( \frac{x^2}{x} \) simplifies directly to \( x \), which is already in its simplest form. |
Additional Resources for Further Learning
Explore these resources to deepen your understanding of \( x^2 \) divided by \( x \):
- Read more about algebraic simplification techniques on reputable educational websites.
- Practice problems and solutions related to polynomial division and simplification.
- Watch video tutorials explaining division of algebraic expressions.
- Engage in online forums to discuss and ask questions about algebraic concepts.
- Consult textbooks or e-books focusing on algebra and advanced mathematics.
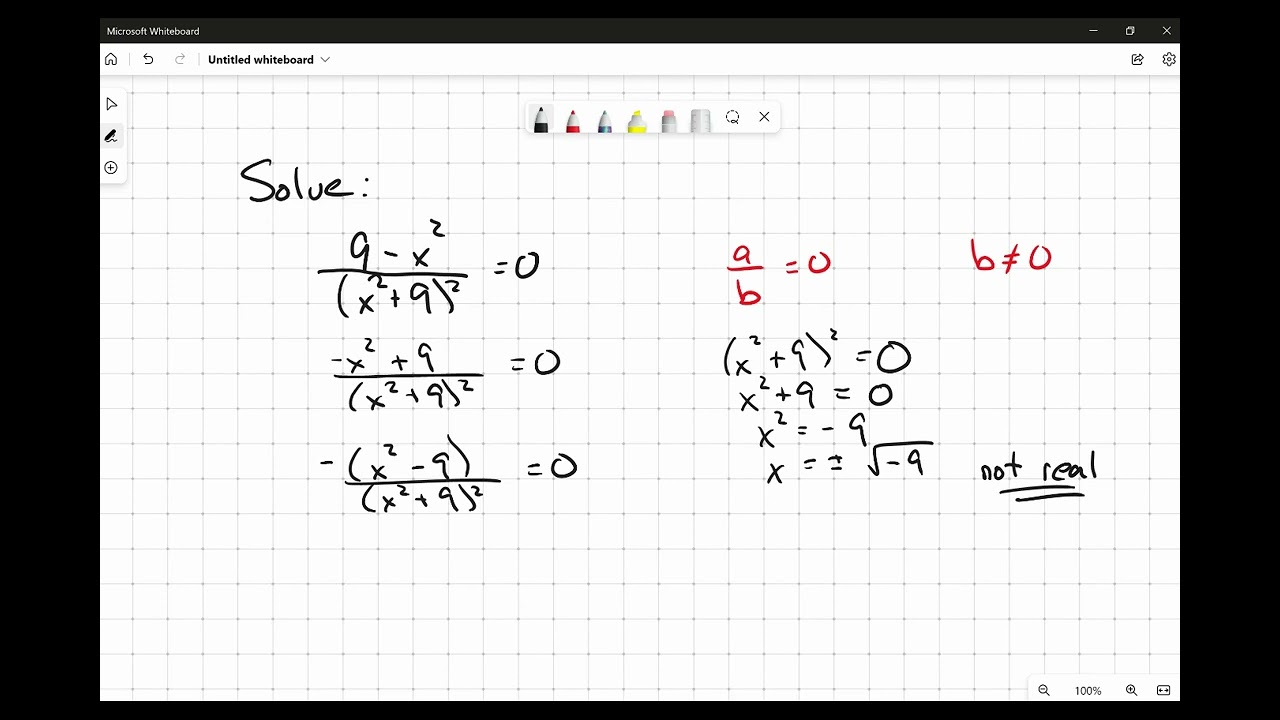
Giải bài toán: Giải phương trình chín trừ x bình phương chia cho x bình phương cộng chín bình phương bằng không. Xem video để hiểu rõ hơn.
Solve nine minus x squared divided by x squared plus nine squared equals zero - Video
READ MORE:
Tìm hiểu cách đơn giản hóa biểu thức phức tạp này một cách dễ dàng và nhanh chóng.
Đơn giản hóa một chia cho x cộng h bình phương trừ một chia cho x bình phương chia cho h


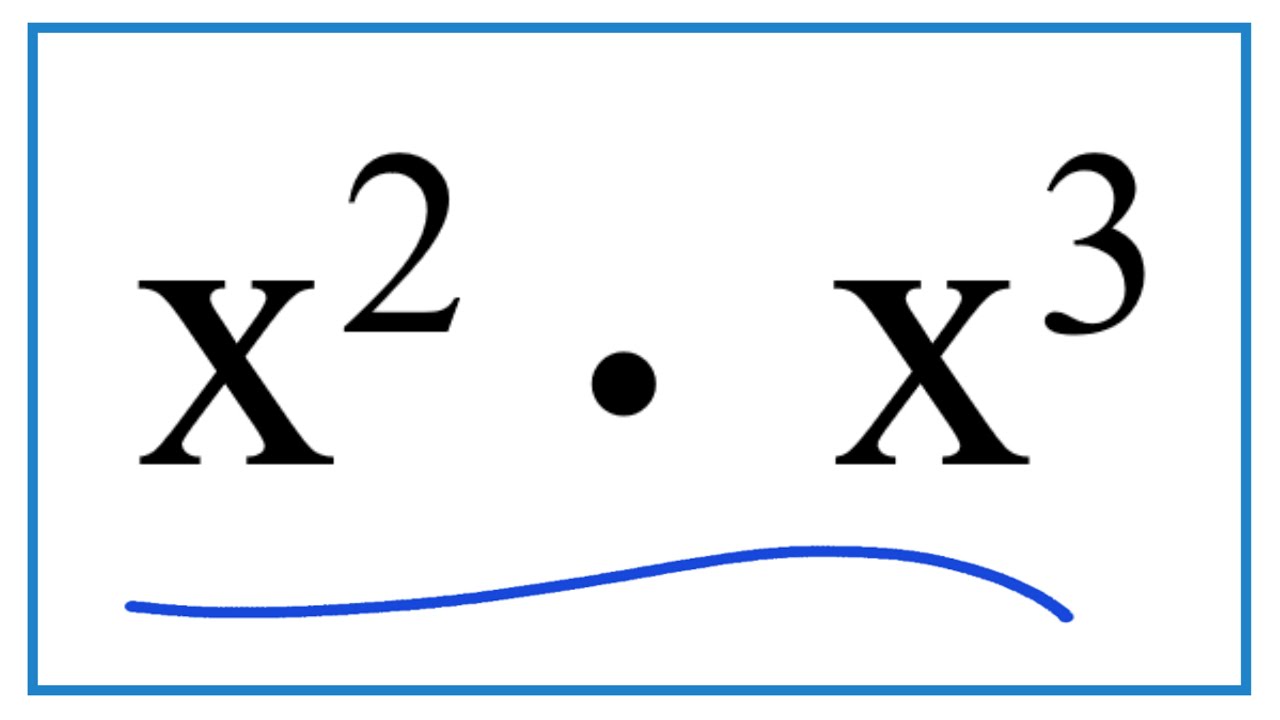



x-1=sec(squared)x.jpg)






