Topic derivative of e to the x squared: Explore the fascinating world of calculus by delving into the derivative of e to the x squared. This article provides a clear explanation of how to differentiate this complex exponential function step-by-step. Gain insights into its applications in mathematics and beyond, and enhance your understanding with practical examples and common pitfalls to avoid.
Table of Content
- Understanding the Derivative of \( e^{x^2} \)
- Table of Contents
- 1. Introduction to Derivative of e to the x squared
- 2. Understanding e to the x squared Function
- 3. Step-by-Step Derivation Techniques
- 4. Applications in Calculus and Mathematics
- 5. Advanced Topics and Variations
- 6. Practical Examples and Exercises
- 7. Common Mistakes and How to Avoid Them
- 8. Conclusion and Summary
- YOUTUBE: Xem video về Đạo hàm của e^x^2 (Luật Chuỗi) để học các bài tập Calculus 1 liên quan đến đề tài này.
Understanding the Derivative of \( e^{x^2} \)
The derivative of the function \( e^{x^2} \) is a fundamental concept in calculus, particularly useful in various applications across science and engineering. This document outlines the step-by-step process to differentiate this exponential function.
Formula for the Derivative of \( e^{x^2} \)
The derivative of \( e^{x^2} \) is given by:
\[ \frac{d}{dx}(e^{x^2}) = 2xe^{x^2} \]
Proof Using the Chain Rule
To derive \( \frac{d}{dx}(e^{x^2}) \) using the chain rule:
- Let \( u = x^2 \), then \( e^{x^2} = e^u \).
- Differentiate \( u \) with respect to \( x \): \( \frac{du}{dx} = 2x \).
- Apply the chain rule: \( \frac{d}{dx}(e^u) = e^u \cdot \frac{du}{dx} \).
Combining these results, we get:
\[ \frac{d}{dx}(e^{x^2}) = e^{x^2} \cdot 2x = 2xe^{x^2} \]
Alternative Methods of Proof
First Principle of Derivatives
Using the first principle, we start with the limit definition:
\[ f'(x) = \lim_{h \to 0} \frac{e^{(x+h)^2} - e^{x^2}}{h} \]
Expanding and simplifying, we find:
\[ f'(x) = \lim_{h \to 0} \frac{e^{x^2 + 2xh + h^2} - e^{x^2}}{h} = e^{x^2} \cdot 2x = 2xe^{x^2} \]
Product Rule
Another way to find the derivative is by treating \( e^{x^2} \) as a product:
Let \( f(x) = e^{x^2} \cdot 1 \).
Applying the product rule:
\[ f'(x) = \frac{d}{dx}(e^{x^2}) \cdot 1 + e^{x^2} \cdot \frac{d}{dx}(1) = 2xe^{x^2} \]
Examples and Applications
Let's explore a few examples to solidify our understanding:
- Find the derivative of \( y = e^{x^2} \):
\[ \frac{dy}{dx} = 2xe^{x^2} \] - Differentiate \( y = e^{3x^2} \):
\[ \frac{dy}{dx} = 6xe^{3x^2} \]
Using Online Tools
For complex derivatives or verification, online calculators can be very helpful. You can input the function \( e^{x^2} \) into a derivative calculator to get quick results and step-by-step solutions.
Summary
The derivative of \( e^{x^2} \) is an essential result in calculus, demonstrating the application of the chain rule and other differentiation techniques. Understanding this process allows for deeper insights into the behavior of exponential functions.

READ MORE:
Table of Contents
In this comprehensive guide, we will delve into the derivative of \( e^{x^2} \), exploring its intricacies and applications in calculus and mathematics. Here's a structured breakdown of what you can expect:
1. Introduction to Derivative of e to the x squared
The derivative of \( e^{x^2} \) is a fundamental concept in calculus, essential for understanding the rate of change of this exponential function. Let's explore the basics:
- Definition and Notation
- Key Properties and Behavior
- Derivation Techniques
- Graphical Representation
- Applications in Science and Engineering
2. Understanding e to the x squared Function
The function \( e^{x^2} \), also known as the exponential of a quadratic function, exhibits unique characteristics in calculus and mathematical analysis. Here's a comprehensive look at its properties:
- Definition and Representation
- Domain and Range
- Behavior and Symmetry
- Graphical Interpretation
- Applications in Probability and Statistics
3. Step-by-Step Derivation Techniques
Deriving the derivative of \( e^{x^2} \) involves several precise steps and mathematical operations. Here’s a structured approach:
- Apply the chain rule to differentiate \( e^{x^2} \).
- Simplify the expression using exponentiation rules.
- Calculate the derivative step-by-step.
- Verify the result for accuracy.
- Explore alternative methods for derivation.
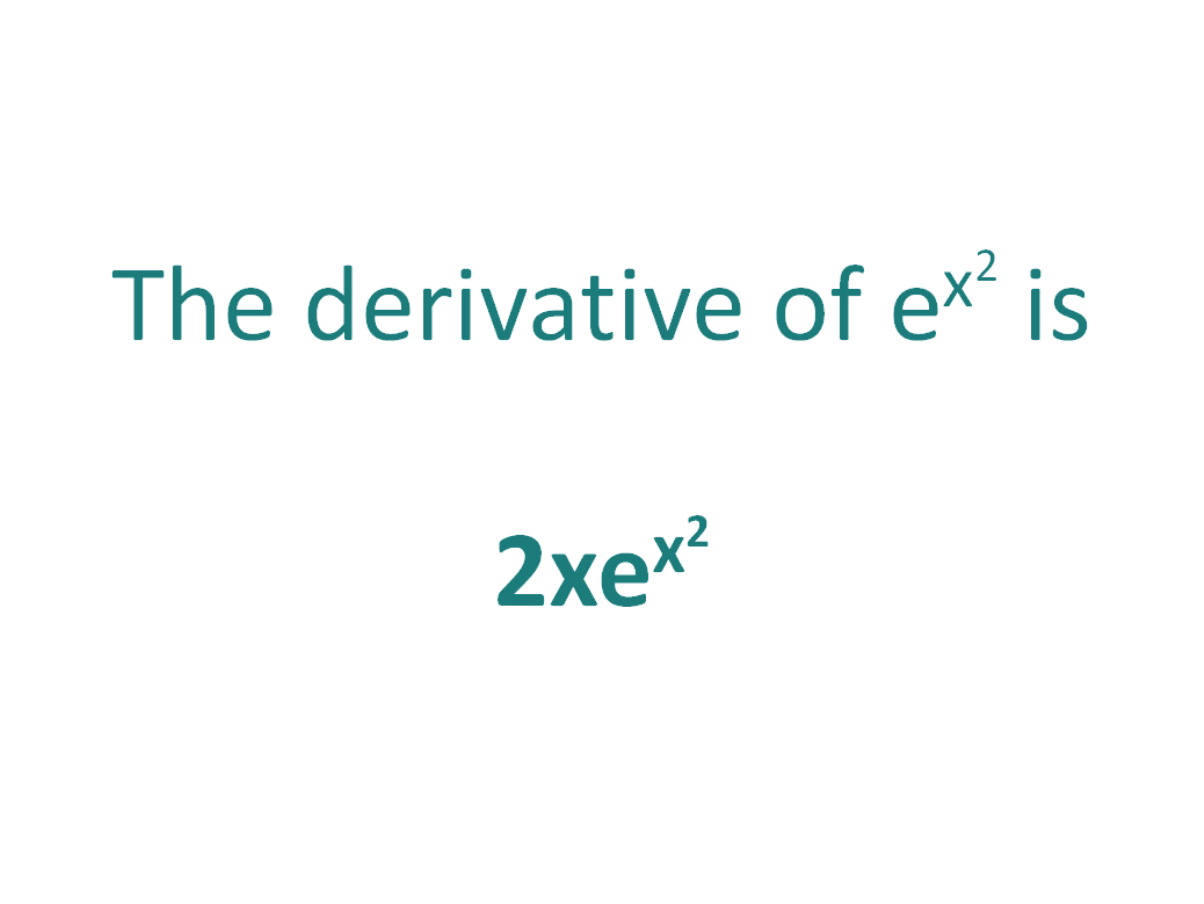
4. Applications in Calculus and Mathematics
The derivative of \( e^{x^2} \) finds numerous applications across various fields of calculus and mathematics, showcasing its versatility and importance. Here are some notable applications:
- Rate of Change Analysis
- Optimization Problems
- Curve Sketching and Analysis
- Integration Techniques
- Probability and Statistics
5. Advanced Topics and Variations
Exploring advanced topics and variations of the derivative of \( e^{x^2} \) opens up new dimensions in calculus and mathematical analysis. Here are some intricate aspects to consider:
- Higher Order Derivatives
- Partial Derivatives and Multivariable Functions
- Series Expansion Techniques
- Application to Differential Equations
- Complex Analysis and Special Functions
6. Practical Examples and Exercises
Practical examples and exercises involving the derivative of \( e^{x^2} \) reinforce understanding and application of this concept in real-world scenarios. Here are some exercises to enhance your proficiency:
- Compute the derivative of \( e^{x^2} \) at specific points.
- Investigate the behavior of \( e^{x^2} \) using its derivative.
- Solve optimization problems using \( e^{x^2} \).
- Explore applications in physics and engineering.
- Construct graphs illustrating the derivative’s impact.
7. Common Mistakes and How to Avoid Them
Identifying common mistakes in differentiating \( e^{x^2} \) and understanding strategies to prevent them can streamline your learning process. Here’s a guide to avoid pitfalls:
- Incorrect application of the chain rule.
- Misinterpreting the exponentiation rule.
- Errors in algebraic manipulation.
- Confusion with the function composition.
- Forgetting to check for correctness of the final result.

8. Conclusion and Summary
In conclusion, exploring the derivative of \( e^{x^2} \) reveals its significance in calculus and mathematics. This guide has covered:
- The definition and properties of \( e^{x^2} \).
- Step-by-step techniques to derive its derivative.
- Applications across various fields, including optimization and differential equations.
- Advanced topics such as higher-order derivatives and complex analysis.
- Common mistakes to avoid when differentiating \( e^{x^2} \).
Understanding these aspects enhances problem-solving skills and deepens comprehension of exponential functions in mathematical contexts.
Xem video về Đạo hàm của e^x^2 (Luật Chuỗi) để học các bài tập Calculus 1 liên quan đến đề tài này.
Đạo hàm của e^x^2 (Luật Chuỗi) | Bài Tập Calculus 1
READ MORE:
Tìm đạo hàm bậc hai của hàm số y = e^(x^2)








:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)



