Topic square roots and cube roots worksheet with answers pdf: Looking to master square roots and cube roots? Our comprehensive worksheet with answers in PDF format is perfect for students and educators alike. This resource covers everything from basic calculations to real-life applications, offering practice problems and solutions to enhance your understanding and proficiency in these essential mathematical concepts.
Table of Content
- Square Roots and Cube Roots Worksheet with Answers
- Introduction to Square Roots and Cube Roots
- Basics of Square Roots
- Calculating Square Roots
- Understanding Cube Roots
- Properties of Square Roots
- Properties of Cube Roots
- Practice Problems for Square Roots
- Practice Problems for Cube Roots
- Mixed Practice Problems
- Word Problems Involving Square Roots
- Word Problems Involving Cube Roots
- Answer Key for Square Roots Practice Problems
- Answer Key for Cube Roots Practice Problems
- Answer Key for Mixed Practice Problems
- Tips and Tricks for Solving Square Roots
- Tips and Tricks for Solving Cube Roots
- Applications of Square Roots in Real Life
- Applications of Cube Roots in Real Life
- YOUTUBE: Video giải thích các khái niệm về lũy thừa và căn bậc hai, cung cấp kiến thức cơ bản và ví dụ minh họa cho học sinh và người mới bắt đầu.
Square Roots and Cube Roots Worksheet with Answers
This worksheet focuses on solving problems related to square roots and cube roots. Below, you will find a series of exercises along with detailed answers. These exercises are designed to strengthen your understanding of roots and prepare you for more advanced mathematical concepts.
Contents
Understanding Square Roots
The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). The square root function is denoted as \( \sqrt{x} \). For example:
- \(\sqrt{9} = 3\) because \(3^2 = 9\)
- \(\sqrt{16} = 4\) because \(4^2 = 16\)
- \(\sqrt{25} = 5\) because \(5^2 = 25\)
Calculating Cube Roots
The cube root of a number \( x \) is a number \( y \) such that \( y^3 = x \). The cube root function is denoted as \( \sqrt[3]{x} \). For example:
- \(\sqrt[3]{8} = 2\) because \(2^3 = 8\)
- \(\sqrt[3]{27} = 3\) because \(3^3 = 27\)
- \(\sqrt[3]{64} = 4\) because \(4^3 = 64\)
Practice Problems
| Problem | Solution |
| \(\sqrt{49}\) | 7 |
| \(\sqrt[3]{125}\) | 5 |
| \(\sqrt{81}\) | 9 |
| \(\sqrt[3]{216}\) | 6 |
| \(\sqrt{121}\) | 11 |
| \(\sqrt[3]{343}\) | 7 |
Answers
- \(\sqrt{49} = 7\)
- \(\sqrt[3]{125} = 5\)
- \(\sqrt{81} = 9\)
- \(\sqrt[3]{216} = 6\)
- \(\sqrt{121} = 11\)
- \(\sqrt[3]{343} = 7\)
Practice these problems regularly to master the concepts of square roots and cube roots!

READ MORE:
Introduction to Square Roots and Cube Roots
Understanding square roots and cube roots is fundamental to mastering higher-level mathematics. These concepts are essential for solving equations, simplifying expressions, and analyzing real-world problems. In this section, we will explore the basics of square roots and cube roots, their properties, and methods to calculate them.
Square Roots:
The square root of a number \(x\) is a value \(y\) such that \(y^2 = x\). In other words, if you multiply \(y\) by itself, you get \(x\). The square root is represented as \(\sqrt{x}\).
For example:
- \(\sqrt{16} = 4\) because \(4^2 = 16\)
- \(\sqrt{25} = 5\) because \(5^2 = 25\)
Cube Roots:
The cube root of a number \(x\) is a value \(y\) such that \(y^3 = x\). This means if you multiply \(y\) by itself three times, you get \(x\). The cube root is represented as \(\sqrt[3]{x}\).
For example:
- \(\sqrt[3]{27} = 3\) because \(3^3 = 27\)
- \(\sqrt[3]{64} = 4\) because \(4^3 = 64\)
Properties of Square Roots:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \(\sqrt{a^2} = |a|\)
Properties of Cube Roots:
- \(\sqrt[3]{a \cdot b} = \sqrt[3]{a} \cdot \sqrt[3]{b}\)
- \(\sqrt[3]{\frac{a}{b}} = \frac{\sqrt[3]{a}}{\sqrt[3]{b}}\)
- \(\sqrt[3]{a^3} = a\)
By mastering these fundamental properties and understanding how to calculate square roots and cube roots, you will be better prepared to tackle more complex mathematical problems.
Basics of Square Roots
Square roots are a foundational concept in mathematics, representing a number that, when multiplied by itself, yields the original number. Understanding how to calculate and simplify square roots is crucial for solving various mathematical problems.
Definition:
The square root of a number \(x\) is a value \(y\) such that \(y^2 = x\). It is denoted as \(\sqrt{x}\).
Examples:
- \(\sqrt{9} = 3\) because \(3^2 = 9\)
- \(\sqrt{16} = 4\) because \(4^2 = 16\)
- \(\sqrt{1} = 1\) because \(1^2 = 1\)
Properties of Square Roots:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \(\sqrt{a^2} = |a|\)
- \(\sqrt{0} = 0\)
- Square roots of negative numbers are not real numbers (they are imaginary numbers).
Steps to Calculate Square Roots:
- Prime Factorization: Break down the number into its prime factors.
- Pairing Factors: Pair the prime factors.
- Taking One Factor from Each Pair: For each pair of prime factors, take one factor out of the square root.
For example, to find the square root of 36:
- Prime factorization of 36: \(36 = 2^2 \times 3^2\)
- Pairing factors: \((2^2)\) and \((3^2)\)
- Taking one factor from each pair: \(2 \times 3 = 6\)
So, \(\sqrt{36} = 6\).
Simplifying Square Roots:
To simplify square roots, look for perfect square factors.
- \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\)
- \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\)
Understanding these basics will help you solve more complex problems involving square roots and enhance your overall mathematical skills.
Calculating Square Roots
Calculating square roots is a vital skill in mathematics, allowing us to find the original number that was squared to get a given value. There are various methods to calculate square roots, ranging from manual calculations to using calculators. Here, we will explore some fundamental techniques.
Method 1: Prime Factorization
- Find Prime Factors: Break down the number into its prime factors.
- Example: \(36 = 2 \times 2 \times 3 \times 3\)
- Pair the Factors: Group the prime factors into pairs.
- Example: \((2 \times 2) \text{ and } (3 \times 3)\)
- Take One Factor from Each Pair: For each pair of prime factors, take one factor out of the square root.
- Example: \(\sqrt{36} = \sqrt{(2 \times 2) \times (3 \times 3)} = 2 \times 3 = 6\)
Method 2: Estimation
- Identify Perfect Squares: Find the perfect squares nearest to the number.
- Example: For \(\sqrt{50}\), the nearest perfect squares are \(49 \text{ (7}^2\text{)}\) and \(64 \text{ (8}^2\text{)}\).
- Estimate: Determine that \(\sqrt{50}\) is slightly more than 7 but less than 8.
- Refine the Estimate: Use average method or a calculator to refine the estimate.
- Example: \(\sqrt{50} \approx 7.07\)
Method 3: Long Division Method
- Pair the Digits: Starting from the decimal point, pair the digits of the number in twos.
- Example: For \(1521\), pair as \(15 \text{ and } 21\).
- Find the Largest Integer: Find the largest integer whose square is less than or equal to the first pair.
- Example: For \(15\), the largest integer is 3 (since \(3^2 = 9\) and \(4^2 = 16\)).
- Subtract and Bring Down: Subtract the square of this integer from the first pair, then bring down the next pair of digits.
- Example: \(15 - 9 = 6\), bring down 21 to get 621.
- Double the Quotient: Double the quotient obtained and determine the next digit.
- Example: Quotient is 3, double it to get 6. Determine a digit \(d\) such that \(6d \times d \leq 621\).
- Repeat: Repeat the process until you have the desired precision.
Using these methods, you can accurately calculate the square roots of various numbers, enhancing your mathematical problem-solving skills.
Understanding Cube Roots
Cube roots are an essential mathematical concept, representing a number that, when multiplied by itself three times, results in the original number. Understanding how to calculate and simplify cube roots is crucial for solving various mathematical problems.
Definition:
The cube root of a number \(x\) is a value \(y\) such that \(y^3 = x\). It is denoted as \(\sqrt[3]{x}\).
Examples:
- \(\sqrt[3]{8} = 2\) because \(2^3 = 8\)
- \(\sqrt[3]{27} = 3\) because \(3^3 = 27\)
- \(\sqrt[3]{64} = 4\) because \(4^3 = 64\)
Properties of Cube Roots:
- \(\sqrt[3]{a \cdot b} = \sqrt[3]{a} \cdot \sqrt[3]{b}\)
- \(\sqrt[3]{\frac{a}{b}} = \frac{\sqrt[3]{a}}{\sqrt[3]{b}}\)
- \(\sqrt[3]{a^3} = a\)
- Cube roots of negative numbers are real numbers (e.g., \(\sqrt[3]{-8} = -2\)).
Steps to Calculate Cube Roots:
- Prime Factorization: Break down the number into its prime factors.
- Example: \(64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6\)
- Group the Factors: Group the prime factors into triples.
- Example: \((2 \times 2 \times 2) \text{ and } (2 \times 2 \times 2)\)
- Take One Factor from Each Group: For each group of three prime factors, take one factor out of the cube root.
- Example: \(\sqrt[3]{64} = \sqrt[3]{2^6} = 2^2 = 4\)
Method 2: Estimation
- Identify Perfect Cubes: Find the perfect cubes nearest to the number.
- Example: For \(\sqrt[3]{50}\), the nearest perfect cubes are \(27 \text{ (3}^3\text{)}\) and \(64 \text{ (4}^3\text{)}\).
- Estimate: Determine that \(\sqrt[3]{50}\) is slightly more than 3 but less than 4.
- Refine the Estimate: Use average method or a calculator to refine the estimate.
- Example: \(\sqrt[3]{50} \approx 3.68\)
Applications of Cube Roots:
Cube roots are widely used in various fields such as physics, engineering, and computer graphics. For instance, they help in calculating volumes, determining the side length of a cube given its volume, and understanding scaling in three-dimensional space.
Mastering the calculation of cube roots will enhance your ability to solve complex mathematical and real-world problems.

Properties of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. Square roots have several important properties that can help in simplifying and solving mathematical problems. Here are the key properties of square roots:
-
Non-negative Results:
The square root of any non-negative number is always non-negative. This is because a negative times a negative is a positive, so we define the principal (or positive) square root.
\[ \sqrt{x} \geq 0 \text{ for } x \geq 0 \]
-
Product Property:
The square root of a product is the product of the square roots. This property is useful for simplifying complex expressions.
\[ \sqrt{ab} = \sqrt{a} \times \sqrt{b} \]
-
Quotient Property:
The square root of a quotient is the quotient of the square roots. This is helpful for dividing numbers under the square root sign.
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \text{ for } b \neq 0 \]
-
Power Property:
Taking the square root of a number squared returns the original number. This property is based on the definition of square roots.
\[ \sqrt{x^2} = |x| \]
Note that the absolute value is used to ensure the result is non-negative.
-
Addition and Subtraction:
Square roots of sums or differences cannot be separated into individual square roots. This is a common misconception to avoid.
\[ \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \]
\[ \sqrt{a - b} \neq \sqrt{a} - \sqrt{b} \]
Here are some examples to illustrate these properties:
| Expression | Simplified Form |
|---|---|
| \( \sqrt{16} \) | 4 |
| \( \sqrt{4 \times 9} \) | \( \sqrt{4} \times \sqrt{9} = 2 \times 3 = 6 \) |
| \( \sqrt{\frac{25}{4}} \) | \( \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2} \) |
| \( \sqrt{9 + 16} \) | \( \sqrt{25} = 5 \) (not \( \sqrt{9} + \sqrt{16} = 3 + 4 = 7 \)) |
| \( \sqrt{(3)^2} \) | \( |3| = 3 \) |
Understanding these properties can greatly assist in solving equations and simplifying expressions involving square roots.
Properties of Cube Roots
Cube roots have unique properties that are useful in mathematical problem-solving. The cube root of a number x is a value that, when multiplied by itself three times, gives x. It is denoted as ∛x or x1/3. Here are the key properties of cube roots:
-
Real and Unique:
Every real number has a unique real cube root. This includes both positive and negative numbers.
\[ \text{If } x \text{ is a real number, then } \sqrt[3]{x} \text{ is also a real number.} \]
-
Sign Preservation:
The cube root of a positive number is positive, and the cube root of a negative number is negative. This property differentiates cube roots from square roots.
\[ \sqrt[3]{-x} = -\sqrt[3]{x} \]
-
Product Property:
The cube root of a product is the product of the cube roots. This property helps in simplifying multiplication under the cube root sign.
\[ \sqrt[3]{ab} = \sqrt[3]{a} \times \sqrt[3]{b} \]
-
Quotient Property:
The cube root of a quotient is the quotient of the cube roots. This is useful for dividing numbers under the cube root sign.
\[ \sqrt[3]{\frac{a}{b}} = \frac{\sqrt[3]{a}}{\sqrt[3]{b}} \text{ for } b \neq 0 \]
-
Addition and Subtraction:
Cube roots of sums or differences cannot be separated into individual cube roots. This is a common misconception to avoid.
\[ \sqrt[3]{a + b} \neq \sqrt[3]{a} + \sqrt[3]{b} \]
\[ \sqrt[3]{a - b} \neq \sqrt[3]{a} - \sqrt[3]{b} \]
Here are some examples to illustrate these properties:
| Expression | Simplified Form |
|---|---|
| \( \sqrt[3]{8} \) | 2 |
| \( \sqrt[3]{-27} \) | -3 |
| \( \sqrt[3]{8 \times 27} \) | \( \sqrt[3]{8} \times \sqrt[3]{27} = 2 \times 3 = 6 \) |
| \( \sqrt[3]{\frac{64}{8}} \) | \( \frac{\sqrt[3]{64}}{\sqrt[3]{8}} = \frac{4}{2} = 2 \) |
| \( \sqrt[3]{-125} \) | -5 |
Understanding these properties can greatly assist in solving equations and simplifying expressions involving cube roots.
Practice Problems for Square Roots
Below are several practice problems to help you master calculating square roots. Solve each problem step-by-step using the appropriate method and verify your answers with the provided solutions.
Problem Set:
-
Find the square root of 144.
Solution: \( \sqrt{144} = 12 \)
-
Calculate the square root of 256.
Solution: \( \sqrt{256} = 16 \)
-
Determine the square root of 1024.
Solution: \( \sqrt{1024} = 32 \)
-
What is the square root of 49?
Solution: \( \sqrt{49} = 7 \)
-
Find the square root of 900.
Solution: \( \sqrt{900} = 30 \)
-
Calculate the square root of 64.
Solution: \( \sqrt{64} = 8 \)
-
Determine the square root of 169.
Solution: \( \sqrt{169} = 13 \)
-
What is the square root of 361?
Solution: \( \sqrt{361} = 19 \)
Advanced Problems:
-
Find the square root of 2025 by the prime factorization method.
Solution:
Prime factorization of 2025: \( 3 \times 3 \times 3 \times 3 \times 5 \times 5 \)
Pairs: \( (3 \times 3), (3 \times 3), (5 \times 5) \)
Therefore, \( \sqrt{2025} = 3 \times 3 \times 5 = 45 \) -
Determine the square root of 4096 using the long division method.
Solution:
Using long division, we find \( \sqrt{4096} = 64 \)
Challenge Problems:
-
Find the value of \( \sqrt{12544} \).
Solution: \( \sqrt{12544} = 112 \)
-
Calculate the square root of 1444 by the prime factorization method.
Solution:
Prime factorization of 1444: \( 2 \times 2 \times 19 \times 19 \)
Pairs: \( (2 \times 2), (19 \times 19) \)
Therefore, \( \sqrt{1444} = 2 \times 19 = 38 \)
Practice Problems for Cube Roots
Practice solving the following problems to master the concept of cube roots. Use different methods such as prime factorization, estimation, and calculators as needed. Answers are provided at the end.
- Find the cube root of 8
- Find the cube root of 27
- Find the cube root of 64
- Find the cube root of 125
- Find the cube root of 216
- Find the cube root of 343
- Estimate the cube root of 50
- Estimate the cube root of 100
- Find the cube root of -27
- Find the cube root of -64
Steps and Solutions
| Problem | Step-by-Step Solution |
|---|---|
| 1. ∛8 |
The prime factors of 8 are 2 x 2 x 2. Grouping in sets of three: (2 x 2 x 2) The cube root is 2. |
| 2. ∛27 |
The prime factors of 27 are 3 x 3 x 3. Grouping in sets of three: (3 x 3 x 3) The cube root is 3. |
| 3. ∛64 |
The prime factors of 64 are 2 x 2 x 2 x 2 x 2 x 2. Grouping in sets of three: (2 x 2 x 2) and (2 x 2 x 2) The cube root is 4. |
| 4. ∛125 |
The prime factors of 125 are 5 x 5 x 5. Grouping in sets of three: (5 x 5 x 5) The cube root is 5. |
| 5. ∛216 |
The prime factors of 216 are 2 x 2 x 2 x 3 x 3 x 3. Grouping in sets of three: (2 x 2 x 2) and (3 x 3 x 3) The cube root is 6. |
| 6. ∛343 |
The prime factors of 343 are 7 x 7 x 7. Grouping in sets of three: (7 x 7 x 7) The cube root is 7. |
| 7. ∛50 (Estimation) |
Round 50 to the nearest perfect cube, which is 64. Find the cube root of 64: ∛64 = 4. The cube root of 50 is approximately 3.7. |
| 8. ∛100 (Estimation) |
Round 100 to the nearest perfect cube, which is 125. Find the cube root of 125: ∛125 = 5. The cube root of 100 is approximately 4.6. |
| 9. ∛-27 |
The prime factors of -27 are -3 x -3 x -3. Grouping in sets of three: (-3 x -3 x -3) The cube root is -3. |
| 10. ∛-64 |
The prime factors of -64 are -2 x -2 x -2 x -2 x -2 x -2. Grouping in sets of three: (-2 x -2 x -2) and (-2 x -2 x -2) The cube root is -4. |
Answer Key
- 2
- 3
- 4
- 5
- 6
- 7
- Approximately 3.7
- Approximately 4.6
- -3
- -4

Mixed Practice Problems
In this section, you will find a variety of problems that involve both square roots and cube roots. Use the appropriate methods to solve each problem and practice your skills in finding roots. Below are several problems for you to solve:
-
Find the square root of 144.
Solution: \(\sqrt{144} = 12\)
-
Find the cube root of 125.
Solution: \(\sqrt[3]{125} = 5\)
-
Solve for \(x\) if \(x^2 = 81\).
Solution: \(x = \pm 9\)
-
Find the value of \(\sqrt{289}\).
Solution: \(\sqrt{289} = 17\)
-
Determine \(\sqrt[3]{27}\).
Solution: \(\sqrt[3]{27} = 3\)
-
Calculate \(\sqrt{100}\).
Solution: \(\sqrt{100} = 10\)
-
What is the cube root of 64?
Solution: \(\sqrt[3]{64} = 4\)
-
Solve for \(y\) if \(y^3 = 8\).
Solution: \(y = 2\)
-
Find the square root of 225.
Solution: \(\sqrt{225} = 15\)
-
Find the cube root of 216.
Solution: \(\sqrt[3]{216} = 6\)
Use these problems to practice and reinforce your understanding of both square roots and cube roots. Check your answers to ensure accuracy and to improve your problem-solving skills.
Word Problems Involving Square Roots
Solve the following word problems involving square roots. Show all your work and write the final answer clearly.
-
Problem 1: A square garden has an area of 144 square meters. What is the length of each side of the garden?
Solution:
To find the length of each side of the square garden, we need to find the square root of the area.
\(\sqrt{144} = 12\)
Therefore, the length of each side of the garden is 12 meters.
-
Problem 2: A square picture frame encloses a picture with an area of 256 square centimeters. What is the length of one side of the picture?
Solution:
To find the length of one side of the square picture, we need to find the square root of the area.
\(\sqrt{256} = 16\)
Therefore, the length of one side of the picture is 16 centimeters.
-
Problem 3: The area of a square field is 400 square meters. How long is the diagonal of the field?
Solution:
First, find the length of one side of the square field.
\(\sqrt{400} = 20\)
To find the diagonal, use the formula for the diagonal of a square: \( \text{diagonal} = s\sqrt{2} \), where \( s \) is the side length.
\(\text{diagonal} = 20\sqrt{2} \approx 28.28\)
Therefore, the length of the diagonal of the field is approximately 28.28 meters.
-
Problem 4: A square-shaped swimming pool has a perimeter of 48 meters. What is the area of the pool?
Solution:
First, find the length of one side of the pool. Since the perimeter of a square is \( 4s \), where \( s \) is the side length:
\(4s = 48 \rightarrow s = 12\)
To find the area, square the side length:
\(s^2 = 12^2 = 144\)
Therefore, the area of the pool is 144 square meters.
-
Problem 5: The side length of a square plot of land is increased by 5 meters, and its new area is 729 square meters. What was the original side length of the plot?
Solution:
Let the original side length be \( s \). After increasing by 5 meters, the new side length is \( s + 5 \).
Set up the equation for the new area:
\((s + 5)^2 = 729\)
Solve for \( s \):
\(s + 5 = \sqrt{729} = 27 \rightarrow s = 27 - 5 = 22\)
Therefore, the original side length of the plot was 22 meters.
Word Problems Involving Cube Roots
Solving word problems involving cube roots can help solidify your understanding of this mathematical concept. Below are several problems to practice, each followed by a detailed solution process.
-
Problem 1: A cube-shaped water tank holds 512 cubic meters of water. What is the length of each side of the tank?
Solution: To find the length of each side of the tank, we need to find the cube root of 512.
\[\sqrt[3]{512} = 8\]
Therefore, each side of the tank is 8 meters long.
-
Problem 2: A shipment of sugar cubes has a total volume of 1,000 cubic centimeters. Each cube has a side length of 1 centimeter. How many sugar cubes are there in the shipment?
Solution: Since each sugar cube is 1 cubic centimeter, we simply need to find the cube root of the total volume to determine the number of cubes along each dimension of the shipment.
\[\sqrt[3]{1000} = 10\]
Therefore, the shipment contains \(10 \times 10 \times 10 = 1,000\) sugar cubes.
-
Problem 3: A large cube is made up of smaller cubes, each with a volume of 1 cubic centimeter. If the large cube has a volume of 27 cubic centimeters, how many smaller cubes are there along one edge of the large cube?
Solution: We need to find the cube root of 27 to determine the number of smaller cubes along one edge.
\[\sqrt[3]{27} = 3\]
Therefore, there are 3 smaller cubes along each edge of the large cube.
-
Problem 4: The volume of a cube is given by \(V = s^3\), where \(s\) is the side length. If the side length of a cube is doubled, how does the volume change?
Solution: Let the original side length be \(s\). The original volume is \(V = s^3\).
If the side length is doubled, the new side length is \(2s\). The new volume is:
\[V_{new} = (2s)^3 = 8s^3\]
The volume increases by a factor of 8.
-
Problem 5: A cube has a volume of 64 cubic meters. What is the length of each side of the cube?
Solution: To find the side length, we need to find the cube root of 64.
\[\sqrt[3]{64} = 4\]
Therefore, each side of the cube is 4 meters long.
Answer Key for Square Roots Practice Problems
Below are the solutions to the practice problems involving square roots. Each problem is solved step-by-step to help you understand the process.
-
Problem: \( \sqrt{25} \)
Solution:
- Identify the number under the square root: 25
- Find the number that, when multiplied by itself, equals 25: \( 5 \times 5 = 25 \)
- Answer: \( \sqrt{25} = 5 \)
-
Problem: \( \sqrt{49} \)
Solution:
- Identify the number under the square root: 49
- Find the number that, when multiplied by itself, equals 49: \( 7 \times 7 = 49 \)
- Answer: \( \sqrt{49} = 7 \)
-
Problem: \( \sqrt{144} \)
Solution:
- Identify the number under the square root: 144
- Find the number that, when multiplied by itself, equals 144: \( 12 \times 12 = 144 \)
- Answer: \( \sqrt{144} = 12 \)
-
Problem: \( \sqrt{81} \)
Solution:
- Identify the number under the square root: 81
- Find the number that, when multiplied by itself, equals 81: \( 9 \times 9 = 81 \)
- Answer: \( \sqrt{81} = 9 \)
-
Problem: \( \sqrt{100} \)
Solution:
- Identify the number under the square root: 100
- Find the number that, when multiplied by itself, equals 100: \( 10 \times 10 = 100 \)
- Answer: \( \sqrt{100} = 10 \)
These answers provide a clear method for solving square root problems. Make sure to practice these steps to become proficient in solving square roots.

Answer Key for Cube Roots Practice Problems
Here are the answers to the practice problems for cube roots. Use these solutions to check your work and ensure you understand how to solve cube root problems correctly.
| Problem | Solution |
|---|---|
| \(\sqrt[3]{27}\) | \(3\) |
| \(\sqrt[3]{64}\) | \(4\) |
| \(\sqrt[3]{125}\) | \(5\) |
| \(\sqrt[3]{216}\) | \(6\) |
| \(\sqrt[3]{343}\) | \(7\) |
| \(\sqrt[3]{512}\) | \(8\) |
| \(\sqrt[3]{729}\) | \(9\) |
| \(\sqrt[3]{1000}\) | \(10\) |
These solutions provide the cube roots of the given numbers, demonstrating how to find the cube root of perfect cubes. If you encountered any difficulties, review the process of calculating cube roots and try the problems again.
Answer Key for Mixed Practice Problems
Below are the answers for the mixed practice problems involving both square roots and cube roots. Each problem is solved step-by-step for better understanding.
-
Problem: Find the square root of 64 and the cube root of 27.
- \(\sqrt{64} = 8\)
- \(\sqrt[3]{27} = 3\)
-
Problem: Find the square root of 144 and the cube root of 64.
- \(\sqrt{144} = 12\)
- \(\sqrt[3]{64} = 4\)
-
Problem: Find the square root of 121 and the cube root of 125.
- \(\sqrt{121} = 11\)
- \(\sqrt[3]{125} = 5\)
-
Problem: Find the square root of 49 and the cube root of 8.
- \(\sqrt{49} = 7\)
- \(\sqrt[3]{8} = 2\)
-
Problem: Find the square root of 81 and the cube root of 1.
- \(\sqrt{81} = 9\)
- \(\sqrt[3]{1} = 1\)
-
Problem: Find the square root of 100 and the cube root of 27.
- \(\sqrt{100} = 10\)
- \(\sqrt[3]{27} = 3\)
-
Problem: Find the square root of 225 and the cube root of 216.
- \(\sqrt{225} = 15\)
- \(\sqrt[3]{216} = 6\)
-
Problem: Find the square root of 36 and the cube root of 125.
- \(\sqrt{36} = 6\)
- \(\sqrt[3]{125} = 5\)
-
Problem: Find the square root of 16 and the cube root of 343.
- \(\sqrt{16} = 4\)
- \(\sqrt[3]{343} = 7\)
-
Problem: Find the square root of 9 and the cube root of 512.
- \(\sqrt{9} = 3\)
- \(\sqrt[3]{512} = 8\)
Tips and Tricks for Solving Square Roots
Solving square roots can be simplified by understanding and applying several tips and tricks. Here are some strategies to help you solve square roots more efficiently:
-
Prime Factorization Method:
- Write the number as a product of its prime factors.
- Pair the prime factors.
- Take one factor from each pair and multiply them together to get the square root.
Example: Find the square root of 144.
- Prime factors of 144: \(144 = 2^4 \times 3^2\)
- Pair the factors: \((2^2 \times 2^2) \times (3^2)\)
- Take one factor from each pair: \(2 \times 3 = 6\)
- The square root of 144 is 12.
-
Using Estimation:
- Find the nearest perfect squares above and below the given number.
- Estimate the square root based on these perfect squares.
Example: Estimate the square root of 50.
- Nearest perfect squares: 49 and 64.
- \(\sqrt{49} = 7\) and \(\sqrt{64} = 8\)
- Estimate: \(\sqrt{50}\) is slightly more than 7 (around 7.1).
-
Using a Calculator:
For non-perfect squares or quick solutions, use a scientific calculator to find the square root. Simply enter the number and press the square root button.
-
Square Root Charts:
Use square root charts to quickly find the square roots of common perfect squares. These charts list numbers and their square roots for easy reference.
-
Long Division Method:
Use the long division method for manual calculation of square roots, especially for larger numbers.
- Group the digits in pairs from right to left.
- Find the largest number whose square is less than or equal to the first group.
- Subtract and bring down the next group of digits, repeating the process.
Example: Find the square root of 2025.
- Group the digits: 20|25
- Largest number whose square is ≤ 20: 4 (since \(4^2 = 16\))
- Subtract and bring down the next pair: 2025 - 1600 = 425
- Double the quotient (4) and find the next digit: 40x * x = 425 (x = 5)
- Result: \(\sqrt{2025} = 45\)
Tips and Tricks for Solving Cube Roots
Solving cube roots can be simplified by understanding and applying several tips and tricks. Here are some strategies to help you solve cube roots more efficiently:
-
Prime Factorization Method:
- Write the number as a product of its prime factors.
- Group the prime factors into triples.
- Take one factor from each triple and multiply them together to get the cube root.
Example: Find the cube root of 216.
- Prime factors of 216: \(216 = 2^3 \times 3^3\)
- Group the factors: \((2^3) \times (3^3)\)
- Take one factor from each group: \(2 \times 3 = 6\)
- The cube root of 216 is 6.
-
Using Estimation:
- Find the nearest perfect cubes above and below the given number.
- Estimate the cube root based on these perfect cubes.
Example: Estimate the cube root of 50.
- Nearest perfect cubes: 27 and 64.
- \(\sqrt[3]{27} = 3\) and \(\sqrt[3]{64} = 4\)
- Estimate: \(\sqrt[3]{50}\) is slightly more than 3 (around 3.7).
-
Using a Calculator:
For non-perfect cubes or quick solutions, use a scientific calculator to find the cube root. Simply enter the number and press the cube root button.
-
Cube Root Charts:
Use cube root charts to quickly find the cube roots of common perfect cubes. These charts list numbers and their cube roots for easy reference.
-
Approximation Method:
- Guess a number that you think is close to the cube root.
- Use the formula: \(x_{n+1} = \frac{2x_n + \frac{N}{x_n^2}}{3}\) where \(x_n\) is your current guess and \(N\) is the number you are finding the cube root of.
- Repeat the process until the result stabilizes.
Example: Find the cube root of 20 using approximation.
- Initial guess: \(x_0 = 3\)
- First iteration: \(x_1 = \frac{2 \times 3 + \frac{20}{3^2}}{3} = \frac{6 + \frac{20}{9}}{3} \approx 2.89\)
- Second iteration: \(x_2 = \frac{2 \times 2.89 + \frac{20}{2.89^2}}{3} \approx 2.71\)
- Continue iterations until the value stabilizes around 2.7.
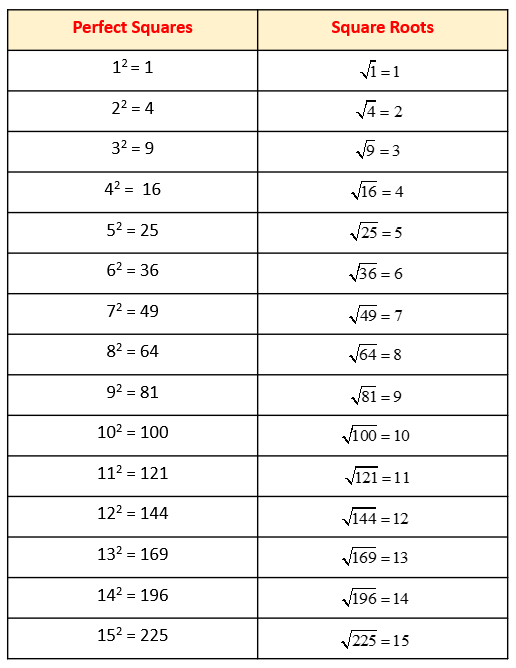
Applications of Square Roots in Real Life
Square roots have numerous applications in various fields of everyday life, science, engineering, and mathematics. Here are some examples of how square roots are used in real-life situations:
-
Architecture and Construction:
Square roots are used to calculate the dimensions of various components in construction and architecture. For example, when determining the length of the diagonal in a rectangular room, the Pythagorean theorem is used, which involves taking the square root of the sum of the squares of the length and width.
Example: For a room with a length of 10 feet and a width of 6 feet, the diagonal length (d) is calculated as:
\[ d = \sqrt{10^2 + 6^2} = \sqrt{100 + 36} = \sqrt{136} \approx 11.66 \text{ feet} \]
-
Physics and Engineering:
In physics, square roots are used in formulas involving areas and distances. For instance, the distance (d) between two points in a 2-dimensional space can be found using the distance formula, which includes a square root.
Example: If point A is at (3, 4) and point B is at (7, 1), the distance (d) is:
\[ d = \sqrt{(7 - 3)^2 + (4 - 1)^2} = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \]
-
Finance:
Square roots are used in financial calculations, such as determining the standard deviation, which is a measure of the amount of variation or dispersion of a set of values. The standard deviation is the square root of the variance.
Example: If the returns of a stock over a period are given, the standard deviation is calculated by finding the square root of the average of the squared deviations from the mean return.
-
Biology:
In biology, square roots are used in statistical calculations, such as in calculating the root mean square error (RMSE) to evaluate the differences between predicted and observed values.
Example: If observed values are \(O_1, O_2, \ldots, O_n\) and predicted values are \(P_1, P_2, \ldots, P_n\), the RMSE is:
\[ RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (O_i - P_i)^2} \]
-
Astronomy:
Square roots are used in various astronomical calculations, such as determining the gravitational force between two objects. The force is inversely proportional to the square of the distance between the objects.
Example: The force (F) between two masses (m_1 and m_2) separated by a distance (r) is given by:
\[ F = G \frac{m_1 m_2}{r^2} \]
Applications of Cube Roots in Real Life
The concept of cube roots is widely applied in various real-life scenarios, helping us understand and solve practical problems. Here are some key applications of cube roots:
-
Volume Calculations:
Cube roots are essential in determining the side length of a cube when its volume is known. This is useful in various fields such as architecture, manufacturing, and packaging. For example, if a cube has a volume of 64 cubic units, its side length is given by \( \sqrt[3]{64} = 4 \) units.
-
Physics and Engineering:
In physics, cube roots are used to calculate properties related to volume and density. For instance, if the density of a material and its mass are known, the volume can be found using cube roots. Similarly, cube roots help in determining the relationship between different physical quantities like pressure, volume, and temperature in gas laws.
-
Biology and Medicine:
Cube roots can be used in biology to understand growth patterns. For example, the growth of cells or the spread of a disease in three-dimensional space can be modeled using cube roots. In medicine, cube roots help in dosing calculations where the volume of distribution and body surface area are considered.
-
Economics and Finance:
In economics, cube roots are applied in calculations involving compound interest and financial growth over time. For example, if an investment grows over a period and the total value is known, the original principal can be calculated using cube roots.
-
Astronomy:
Cube roots are used in astronomy to calculate the distances and volumes of celestial bodies. For example, the mean distance of planets from the sun can be determined using Kepler's third law, which involves cube roots.
Here is a table summarizing some common perfect cubes and their cube roots:
| Number | Perfect Cube | Cube Root |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 8 | 2 |
| 3 | 27 | 3 |
| 4 | 64 | 4 |
| 5 | 125 | 5 |
Understanding and applying cube roots allows us to solve a wide range of practical problems efficiently. These applications highlight the importance of cube roots in various scientific, industrial, and everyday contexts.
Video giải thích các khái niệm về lũy thừa và căn bậc hai, cung cấp kiến thức cơ bản và ví dụ minh họa cho học sinh và người mới bắt đầu.
Toán học Antics - Lũy thừa và Căn bậc hai
READ MORE:
Video hướng dẫn giải bài tập căn bậc hai, giúp học sinh nắm vững kiến thức và làm quen với các dạng bài tập liên quan đến căn bậc hai.
Bài tập Căn bậc hai