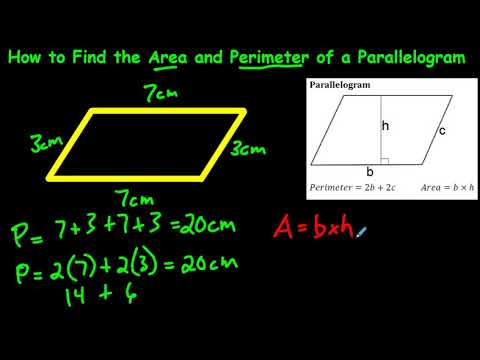
Topic formula of perimeter of right triangle: Understanding the formula of the perimeter of a right triangle is essential for students and professionals alike. This article breaks down the steps to calculate the perimeter effortlessly, with clear examples and practical applications. Whether you're preparing for an exam or solving real-life problems, mastering this formula will enhance your mathematical skills.
Table of Content
- Formula for Perimeter of a Right Triangle
- Introduction to Right Triangles
- Understanding the Perimeter of a Triangle
- Formula for the Perimeter of a Right Triangle
- Derivation of the Perimeter Formula
- Examples of Calculating the Perimeter
- Applications of the Perimeter Formula
- Common Mistakes and How to Avoid Them
- Advanced Problems Involving Right Triangle Perimeters
- Using Technology to Calculate the Perimeter
- Practical Uses in Real Life
- Conclusion and Summary
- YOUTUBE:
Formula for Perimeter of a Right Triangle
The perimeter of a right triangle is the sum of the lengths of all three sides. In a right triangle, the sides are often referred to as the two legs (a and b) and the hypotenuse (c). The formula for the perimeter (P) is given by:
\( P = a + b + c \)
Using the Pythagorean Theorem
If the lengths of the two legs (a and b) are known, we can use the Pythagorean theorem to find the length of the hypotenuse (c). The Pythagorean theorem states:
\( c = \sqrt{a^2 + b^2} \)
Once the hypotenuse is found, the perimeter can be calculated as:
\( P = a + b + \sqrt{a^2 + b^2} \)
Example Calculation
Consider a right triangle with legs of length 5 meters and 12 meters:
- First, calculate the hypotenuse using the Pythagorean theorem:
- Then, find the perimeter:
\( c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \)
\( P = 5 + 12 + 13 = 30 \) meters
Additional Examples
- Example 1: For a triangle with sides of length 8 m, 9 m, and 12.4 m, the perimeter is:
- Example 2: For a triangle with legs of length 8 m and 11 m:
\( P = 8 + 9 + 12.4 = 29.4 \) meters
\( c = \sqrt{8^2 + 11^2} = \sqrt{64 + 121} = \sqrt{185} \approx 13.6 \)
Perimeter: \( P = 8 + 11 + 13.6 = 32.6 \) meters

READ MORE:
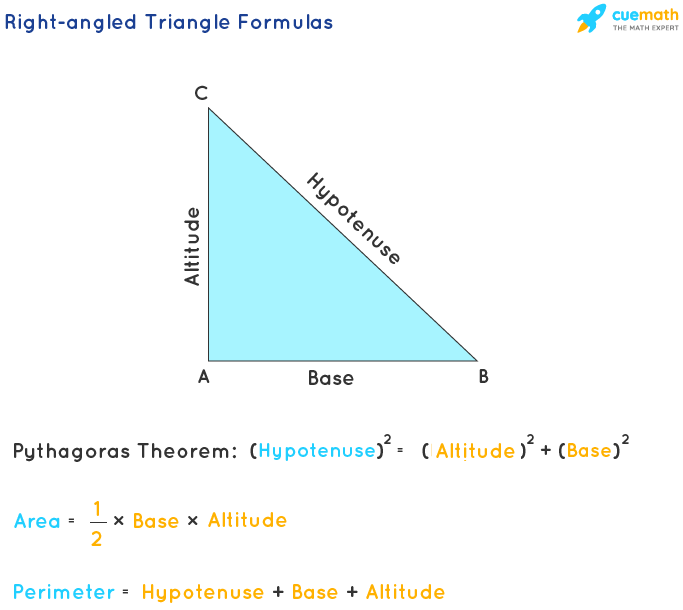
Introduction to Right Triangles
A right triangle is a type of triangle that has one angle measuring 90 degrees. The side opposite this right angle is known as the hypotenuse, which is the longest side of the triangle. The other two sides are referred to as the legs. Right triangles are fundamental in trigonometry and geometry, serving as the basis for various calculations and real-world applications.
Key Characteristics of Right Triangles:
- One angle is exactly 90 degrees.
- The side opposite the right angle is the hypotenuse.
- The two sides adjacent to the right angle are called the legs.
To further understand right triangles, let’s explore their properties and components:
| Component | Description |
| Hypotenuse | The longest side, opposite the right angle. |
| Legs | The two shorter sides that form the right angle. |
Right triangles adhere to the Pythagorean Theorem, which states that:
Here, \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse. This relationship is crucial for calculating the perimeter and other properties of right triangles.
- Identify the lengths of the legs (\(a\) and \(b\)).
- Use the Pythagorean Theorem to find the hypotenuse (\(c\)).
- Apply the perimeter formula: \( \text{Perimeter} = a + b + c \).
Understanding these basics will help you tackle more complex problems involving right triangles.
Understanding the Perimeter of a Triangle
The perimeter of a triangle is the total length of its sides. In a right triangle, which has one 90-degree angle, the perimeter is the sum of the lengths of the two legs and the hypotenuse.
To better understand this concept, let's define the parts of a right triangle:
- Legs: The two sides that form the right angle.
- Hypotenuse: The side opposite the right angle, and the longest side of the triangle.
The formula for calculating the perimeter of any triangle is:
Perimeter = Side 1 + Side 2 + Side 3
In a right triangle, this formula becomes:
Perimeter = Leg 1 + Leg 2 + Hypotenuse
To find the hypotenuse, you can use the Pythagorean theorem, which states:
\( c = \sqrt{a^2 + b^2} \)
where:
- a is one leg of the right triangle
- b is the other leg of the right triangle
- c is the hypotenuse
Therefore, the perimeter formula for a right triangle can also be written as:
Perimeter = Leg 1 + Leg 2 + \(\sqrt{(Leg 1)^2 + (Leg 2)^2}\)
Here's an example to illustrate the calculation:
- If Leg 1 = 3 units and Leg 2 = 4 units:
- First, calculate the hypotenuse:
- Then, calculate the perimeter:
\( Hypotenuse = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) units
Perimeter = 3 + 4 + 5 = 12 units
Understanding these steps ensures accurate calculation of the perimeter in right triangles, whether solving practical problems or engaging in theoretical exercises.
Formula for the Perimeter of a Right Triangle
The perimeter of a right triangle is the sum of the lengths of its three sides. In a right triangle, the sides are usually denoted as:
- a - one of the legs
- b - the other leg
- c - the hypotenuse (the longest side, opposite the right angle)
The formula to calculate the perimeter (P) of a right triangle is straightforward:
\[ P = a + b + c \]
To find the hypotenuse when only the two legs are known, you can use the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} \]
Combining these formulas, the perimeter can be calculated in two steps:
- Calculate the hypotenuse using the Pythagorean theorem.
- Add the lengths of all three sides.
Here's an example to illustrate:
- Given: a = 3 units, b = 4 units
- Calculate the hypotenuse:
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ units} \]
- Calculate the perimeter:
\[ P = 3 + 4 + 5 = 12 \text{ units} \]
Therefore, the perimeter of this right triangle is 12 units.
This method can be applied to any right triangle by substituting the known values of the legs and following the same steps.
Derivation of the Perimeter Formula
The perimeter of a right triangle is the sum of the lengths of its three sides: the two legs and the hypotenuse. To derive the formula for the perimeter, we need to understand the properties of a right triangle.
In a right triangle, the legs are typically denoted as \(a\) and \(b\), and the hypotenuse (the side opposite the right angle) is denoted as \(c\). The Pythagorean theorem states that:
\(c = \sqrt{a^2 + b^2}\)
Using this information, we can express the perimeter \(P\) of the right triangle as the sum of the lengths of the sides:
\(P = a + b + c\)
Substituting the expression for \(c\) from the Pythagorean theorem, we get:
\(P = a + b + \sqrt{a^2 + b^2}\)
Therefore, the formula for the perimeter of a right triangle in terms of its legs \(a\) and \(b\) is:
\(P = a + b + \sqrt{a^2 + b^2}\)
Step-by-Step Derivation
-
Identify the lengths of the legs of the right triangle, denoted as \(a\) and \(b\).
-
Use the Pythagorean theorem to determine the length of the hypotenuse \(c\):
\(c = \sqrt{a^2 + b^2}\)
-
Sum the lengths of all three sides to find the perimeter \(P\):
\(P = a + b + c\)
-
Substitute the expression for \(c\) into the perimeter formula:
\(P = a + b + \sqrt{a^2 + b^2}\)
Example Calculation
Consider a right triangle with legs \(a = 3\) units and \(b = 4\) units. To find the perimeter:
-
Calculate the hypotenuse \(c\):
\(c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\) units
-
Sum the lengths of all three sides:
\(P = 3 + 4 + 5 = 12\) units
Thus, the perimeter of this right triangle is 12 units.
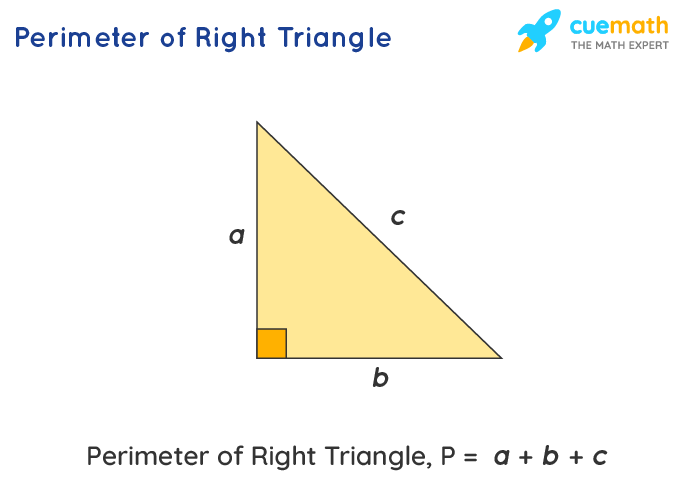
Examples of Calculating the Perimeter
Calculating the perimeter of a right triangle involves summing the lengths of its three sides. Here are a few detailed examples demonstrating this process:
Example 1: Simple Calculation with Known Sides
Given a right triangle with a base of 4 units, a height of 3 units, and a hypotenuse of 5 units, we calculate the perimeter as follows:
- Base \( a = 4 \) units
- Height \( b = 3 \) units
- Hypotenuse \( c = 5 \) units
The perimeter \( P \) is calculated as:
\[ P = a + b + c = 4 + 3 + 5 = 12 \text{ units} \]
Example 2: Using the Pythagorean Theorem
For a right triangle where the base is 6 units and the height is 8 units, we first find the hypotenuse using the Pythagorean theorem:
- Base \( a = 6 \) units
- Height \( b = 8 \) units
Calculate the hypotenuse \( c \):
\[ c = \sqrt{a^2 + b^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ units} \]
Then, the perimeter \( P \) is:
\[ P = a + b + c = 6 + 8 + 10 = 24 \text{ units} \]
Example 3: Finding a Missing Side
If the base of a right triangle is 5 units and the hypotenuse is 13 units, we find the height using the Pythagorean theorem:
- Base \( a = 5 \) units
- Hypotenuse \( c = 13 \) units
Calculate the height \( b \):
\[ b = \sqrt{c^2 - a^2} = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12 \text{ units} \]
Then, the perimeter \( P \) is:
\[ P = a + b + c = 5 + 12 + 13 = 30 \text{ units} \]
Example 4: Mixed Units
Given a right triangle with sides of 7 meters, 24 meters, and 25 meters, we find the perimeter:
- Side 1 \( a = 7 \) meters
- Side 2 \( b = 24 \) meters
- Hypotenuse \( c = 25 \) meters
The perimeter \( P \) is:
\[ P = a + b + c = 7 + 24 + 25 = 56 \text{ meters} \]
Example 5: Hypotenuse and One Side Known
If the base is 9 units and the hypotenuse is 15 units, we calculate the height and then the perimeter:
- Base \( a = 9 \) units
- Hypotenuse \( c = 15 \) units
Calculate the height \( b \):
\[ b = \sqrt{c^2 - a^2} = \sqrt{15^2 - 9^2} = \sqrt{225 - 81} = \sqrt{144} = 12 \text{ units} \]
Then, the perimeter \( P \) is:
\[ P = a + b + c = 9 + 12 + 15 = 36 \text{ units} \]
Applications of the Perimeter Formula
The perimeter of a right triangle has several practical applications in various fields. Understanding these applications can help in real-world problem-solving and enhance our comprehension of geometric principles. Here are some common applications:
-
Construction and Engineering:
In construction, the perimeter of triangular sections is often used to determine the amount of materials needed. For example, if a triangular plot of land needs fencing, knowing the perimeter helps calculate the total length of the fence required.
-
Landscaping:
Landscapers use the perimeter to design and layout triangular garden beds, paths, or decorative elements. The perimeter measurement ensures that the correct amount of border material, such as bricks or edging, is used.
-
Navigation and Surveying:
Surveyors and navigators use the perimeter of right triangles in their calculations for mapping and plotting land. This is especially useful when determining boundaries and property lines in triangular plots.
-
Fabrication and Manufacturing:
In manufacturing, particularly in sheet metal work, the perimeter of triangular components is crucial for cutting and shaping materials accurately to fit design specifications.
-
Education and Problem-Solving:
Understanding the perimeter of right triangles helps in solving various mathematical problems and puzzles, enhancing logical thinking and problem-solving skills.
Let's explore a practical example to see how the perimeter formula is applied:
Example: Fencing a Triangular Park
Suppose we have a triangular park with sides measuring 30 meters, 40 meters, and 50 meters. To determine the amount of fencing needed, we calculate the perimeter.
- Side 1: \(a = 30\) meters
- Side 2: \(b = 40\) meters
- Side 3: \(c = 50\) meters
Using the perimeter formula for a triangle, \(P = a + b + c\), we get:
\[ P = 30 + 40 + 50 = 120 \text{ meters} \]
Therefore, 120 meters of fencing is required to enclose the triangular park.
Conclusion
The perimeter of a right triangle is a fundamental geometric concept with diverse applications in everyday life and various professional fields. Understanding and applying the perimeter formula helps in practical tasks such as construction, landscaping, and manufacturing, demonstrating the importance of geometry in real-world scenarios.
Common Mistakes and How to Avoid Them
Calculating the perimeter of a right triangle can be straightforward, but there are several common mistakes that can lead to incorrect results. Here are some common errors and tips on how to avoid them:
- Ignoring the Pythagorean Theorem:
When you only know the lengths of the legs of the triangle, it's essential to use the Pythagorean theorem to find the length of the hypotenuse. The formula is:
\[ c = \sqrt{a^2 + b^2} \]
Forgetting to apply this theorem can result in an incorrect perimeter calculation.
- Mixing Units:
Always ensure that all measurements are in the same units before performing calculations. Mixing units like meters and centimeters without converting them to a common unit can lead to errors.
- Rounding Errors:
Rounding the lengths of the sides too early in the calculation process can lead to significant inaccuracies. It's best to keep the values as precise as possible until the final step, then round the final perimeter if necessary.
- Forgetting to Add All Sides:
A simple but common mistake is forgetting to add the lengths of all three sides when calculating the perimeter. The formula for the perimeter \( P \) of a right triangle is:
\[ P = a + b + c \]
Ensure you include the hypotenuse and both legs in your sum.
- Incorrect Application of Formulas:
Using incorrect formulas or applying the right formula incorrectly can result in miscalculations. Always double-check your formulas and ensure you understand their application.
By paying close attention to these details and double-checking your calculations, you can avoid these common mistakes and accurately determine the perimeter of a right triangle.
Advanced Problems Involving Right Triangle Perimeters
Advanced problems with right triangle perimeters often involve complex geometric configurations, additional geometric shapes, or the use of trigonometric identities. Here are some advanced examples:
Problem 1: Multiple Right Triangles Sharing a Side
Consider two right triangles, both sharing a common side. Find the perimeter of each triangle given specific side lengths and angles.
- First, calculate the missing side of the right triangle using the Pythagorean theorem.
- Determine the perimeter: \[ P = a + b + c = 15 + 20 + 25 = 60 \]
- For the second triangle sharing the side of length 15, with the other leg being 10: \[ d = \sqrt{15^2 + 10^2} = \sqrt{225 + 100} = \sqrt{325} \approx 18.03 \]
- Calculate the perimeter of the second triangle: \[ P = 15 + 10 + 18.03 \approx 43.03 \]
Given one right triangle with legs \(a = 15\) and \(b = 20\):
\[
c = \sqrt{a^2 + b^2} = \sqrt{15^2 + 20^2} = \sqrt{225 + 400} = \sqrt{625} = 25
\]
Problem 2: Right Triangle within a Circle
Find the perimeter of a right triangle inscribed in a circle where the hypotenuse is the diameter.
- Given the diameter \(d = 30\), the hypotenuse \(c = 30\).
- Use the relationship between the radius and the hypotenuse: \[ c = 2r \Rightarrow r = \frac{c}{2} = 15 \]
- If one leg \(a = 18\), find the other leg using the Pythagorean theorem: \[ b = \sqrt{c^2 - a^2} = \sqrt{30^2 - 18^2} = \sqrt{900 - 324} = \sqrt{576} = 24 \]
- Calculate the perimeter: \[ P = a + b + c = 18 + 24 + 30 = 72 \]
Problem 3: Angle of Elevation
Calculate the perimeter of a right triangle formed by an angle of elevation from a point on the ground to the top of a building.
- Given an angle of elevation \(\theta = 30^\circ\) and the height of the building \(h = 50\).
- Determine the distance from the observer to the base of the building using: \[ \tan(\theta) = \frac{h}{d} \Rightarrow d = \frac{h}{\tan(\theta)} = \frac{50}{\tan(30^\circ)} = \frac{50}{\frac{1}{\sqrt{3}}} = 50\sqrt{3} \approx 86.6 \]
- Calculate the hypotenuse using the Pythagorean theorem: \[ c = \sqrt{h^2 + d^2} = \sqrt{50^2 + (50\sqrt{3})^2} = \sqrt{2500 + 7500} = \sqrt{10000} = 100 \]
- Find the perimeter: \[ P = h + d + c = 50 + 86.6 + 100 \approx 236.6 \]
These problems illustrate how the basic principles of right triangles and the Pythagorean theorem can be applied to solve more complex geometric scenarios. Each step requires careful application of trigonometric identities and geometric properties.
Using Technology to Calculate the Perimeter
Calculating the perimeter of a right triangle can be made simpler with the use of technology. Here are a few methods and tools that can help:
1. Using Online Calculators
Online calculators are widely available and easy to use. Here's how you can calculate the perimeter of a right triangle using an online calculator:
- Open a web browser and search for "right triangle perimeter calculator".
- Select a reliable calculator from the search results.
- Input the lengths of the two legs (a and b) of the right triangle.
- The calculator will automatically compute the hypotenuse (c) using the formula \( c = \sqrt{a^2 + b^2} \).
- The perimeter is then calculated as \( P = a + b + c \) and displayed on the screen.
2. Using Spreadsheet Software (e.g., Microsoft Excel, Google Sheets)
Spreadsheet software can be a powerful tool for calculating the perimeter of a right triangle:
- Open your preferred spreadsheet software.
- In cell A1, enter the length of the first leg (a).
- In cell B1, enter the length of the second leg (b).
- In cell C1, calculate the hypotenuse using the formula: \( =SQRT(A1^2 + B1^2) \).
- In cell D1, calculate the perimeter using the formula: \( =A1 + B1 + C1 \).
3. Using Programming Languages
For those familiar with programming, calculating the perimeter can be automated using simple scripts. Here is an example in Python:
# Function to calculate the perimeter of a right triangle
def perimeter_of_right_triangle(a, b):
c = (a**2 + b**2) ** 0.5
perimeter = a + b + c
return perimeter
# Example usage
a = 3
b = 4
print("The perimeter of the right triangle is:", perimeter_of_right_triangle(a, b))
4. Using Mobile Apps
There are various mobile apps available for both iOS and Android devices that can calculate the perimeter of a right triangle:
- Download and install a geometry calculator app from your app store.
- Open the app and navigate to the right triangle section.
- Enter the lengths of the two legs (a and b).
- The app will calculate the hypotenuse and the perimeter for you.
Using these technological tools can greatly simplify the process of calculating the perimeter of a right triangle, making it quick and efficient.
Practical Uses in Real Life
The perimeter of a right triangle has various practical applications in real life. Here are some examples of how it is used in different fields:
1. Architecture and Construction
In architecture and construction, right triangles are commonly used in the design and construction of buildings and other structures. For instance:
- Calculating the perimeter of a right triangle can help determine the amount of materials needed for building a triangular section of a roof.
- It assists in the layout of stairs, ramps, and other sloped surfaces.
- Ensures precise measurements for cutting materials like wood, metal, or tiles to fit triangular spaces.
2. Navigation and Surveying
Right triangles are essential in navigation and surveying. Here are some applications:
- Surveyors use right triangles to measure distances and plot land boundaries accurately.
- In navigation, the perimeter helps in calculating the shortest path between two points, especially when navigating around obstacles.
3. Engineering
Engineers often use the properties of right triangles in their work, such as:
- Designing mechanical parts that fit together precisely, ensuring the stability and functionality of machines.
- Creating structural components that must withstand specific loads and stresses.
4. Everyday Problem Solving
Understanding the perimeter of a right triangle can be useful in daily life situations:
- Planning and creating garden layouts or any project that involves triangular sections.
- Determining the length of trim needed to frame a triangular window or piece of artwork.
5. Sports and Recreation
In sports and recreation, the concept is used in designing and measuring various playing fields and equipment:
- Calculating distances in track and field events.
- Setting up boundary lines and markers on sports fields, ensuring accurate and fair play areas.
Example Calculation
Let's consider an example where we need to find the perimeter of a right triangle for a real-life application:
- Suppose we are building a triangular garden bed with legs measuring 5 meters and 12 meters.
- First, calculate the hypotenuse using the Pythagorean theorem: \( c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \).
- Then, find the perimeter: \( P = 5 + 12 + 13 = 30 \) meters.
- This perimeter tells us the total length of the edging material needed for the garden bed.
By understanding how to calculate the perimeter of a right triangle, we can solve various practical problems efficiently and accurately in both professional and everyday contexts.
Conclusion and Summary
The study of the perimeter of a right triangle is fundamental in both mathematics and its practical applications. Understanding how to calculate the perimeter allows us to solve a variety of real-world problems efficiently. Here is a summary of what we have covered:
Key Concepts
- A right triangle has one angle of 90 degrees, with the sides opposite this angle known as the legs and the side opposite the right angle called the hypotenuse.
- The perimeter of a right triangle is the sum of the lengths of its three sides.
Formula for Perimeter
The formula for calculating the perimeter of a right triangle is:
\( P = a + b + c \)
Where:
- \( a \) and \( b \) are the lengths of the legs.
- \( c \) is the length of the hypotenuse, calculated using the Pythagorean theorem: \( c = \sqrt{a^2 + b^2} \).
Applications
We explored various practical uses of the perimeter of a right triangle in different fields:
- Architecture and Construction: Planning and building structures, calculating materials.
- Navigation and Surveying: Measuring distances, plotting land boundaries.
- Engineering: Designing mechanical parts, structural components.
- Everyday Problem Solving: Gardening, home improvement projects.
- Sports and Recreation: Setting up fields and equipment.
Using Technology
We also discussed various technological tools to simplify the calculation:
- Online calculators for quick and easy perimeter calculations.
- Spreadsheet software for automated and repeatable calculations.
- Programming languages like Python for custom calculations.
- Mobile apps for on-the-go solutions.
Example Calculation
To illustrate the practical application, consider a right triangle with legs of 5 meters and 12 meters:
- Calculate the hypotenuse: \( c = \sqrt{5^2 + 12^2} = 13 \) meters.
- Calculate the perimeter: \( P = 5 + 12 + 13 = 30 \) meters.
In conclusion, understanding the perimeter of a right triangle and its calculation is a valuable skill with diverse applications in real life. By leveraging both mathematical principles and modern technology, we can efficiently solve various problems and enhance our practical understanding of geometry.
Diện Tích và Chu Vi của Tam Giác Vuông | Toán Học với Thầy J
READ MORE:
Cách Tìm Diện Tích và Chu Vi của Tam Giác Vuông